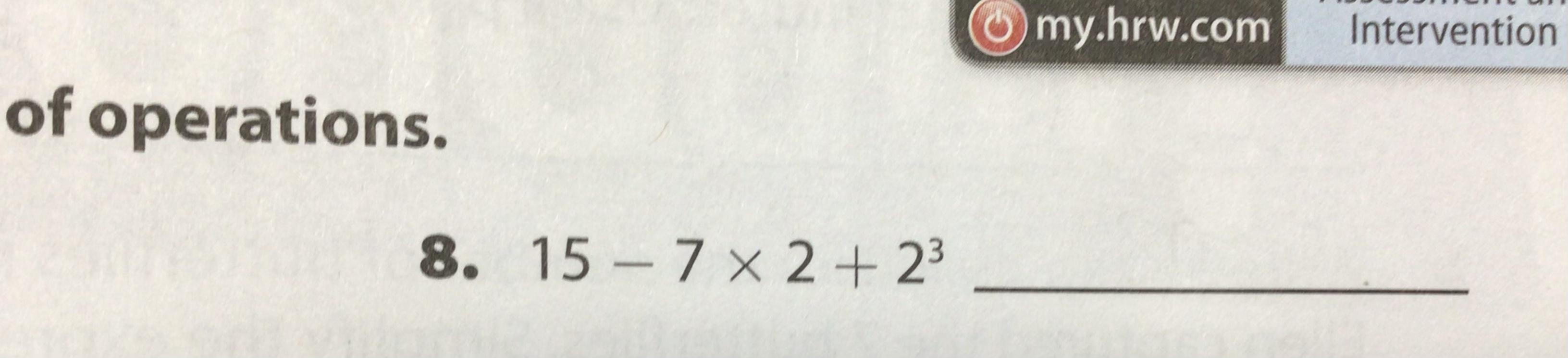Answers
Answer:
5832
Step-by-step explanation:
15 - 7 = 8
8 × 2 = 16
16 + 2 = 18
18 × 18 × 18 = 5832
Related Questions
Write a rule and an equation to fit the pattern in the table.abQuestion content area bottomPart 1Describe the relationship in words.The value of b is 13▼the value of a.
Answers
, the rule is verified.
We are given a table and we need to fit an equation that follows the pattern. We also need to describe the relationship between the two columns in words.Given table,|a|b| |5|65|6|78|8|1010|11|13|13|We see that the value of b is 13 less than the value of a. We can describe this relationship as: "The value of b is 13 less than the value of a."Hence, we can write the rule as:b = a - 13We can check this rule by substituting values from the table in the above equation as follows:When a = 5, b = 5 - 13 = -8When a = 6, b = 6 - 13 = -7When a = 8, b = 8 - 13 = -5When a = 10, b = 10 - 13 = -3When a = 13, b = 13 - 13 = 0The values of b obtained are the same as in the given table.
To know more about, columns visit
https://brainly.com/question/32739397
#SPJ11
Simplify the expression: (12a−1b6c−3) / (4 a5b−1c5) NEED ANSWER IMMEDIATELY PLEASE
Answers
Answer:
Step-by-step explanation:
\(\frac{(12a - 6bc - 3)}{20ab-5c)} \\\\\frac{3 . (4a - 2bc - 1)}{5 . (4ab - c)}\\\\\)
At attorney charges, a fixed fee of $250 for an initial meeting and $150 per hour for all hours worked after that. Find the slope and y-intercept for the data.
slope:
y-intercepy:
Answers
Answer:
slope: 150
y-intercept: 250
y= 150x+250
Step-by-step explanation:
An example of a discrete variable would be
a. the age of players on a hockey team
b. the number of goals scored by players on a hockey team
c. the heights of players on a hockey team
d. the playing time of players on a hockey team
Answers
The number of goals scored by individual players on a hockey team represents an example of a discrete variable.
What is an example of a discrete variable in hockey?In the context of hockey, a discrete variable refers to a characteristic that can only take specific, separate values. The number of goals scored by players on a hockey team is an example of a discrete variable. Each player can score a certain number of goals, and these values are distinct and separate from one another. It is not possible to have fractional or continuous values for the number of goals scored.
Each goal scored is counted as a whole number, making it a discrete variable. Discrete variables, such as the number of goals scored by players in a hockey team, are distinct and separate values that do not fall on a continuum. They are typically counted or enumerated and can only take specific values without any intermediate values between them.
This is in contrast to continuous variables, which can take any value within a given range. Understanding the difference between discrete and continuous variables is essential in various fields, including statistics, mathematics, and data analysis.
Learn more about discrete variable
brainly.com/question/19338975
#SPJ11
Solve for x and y
Please help I forgot what I needed to do!

Answers
Is the table in the picture showing a proportional relationship

Answers
Find the length of KL.

Answers
Answer:
9
Step-by-step explanation:
IL and KL have the same length so we can set them equal.
3x = x+6
Subtract x from each side.
3x-x = x+6-x
2x = 6
Divide by 2.
2x/2 = 6/2
x=3
KL = x+6
=3+6
= 9
Danny had 6 orange colored shirts.this 40% of the shirt he own .how shirts dose Danny own?
Answers
Answer:
15 shirts-----------------------
40% of the total number is 6.
Find the total number x:
0.4x = 6x = 6/0.4x = 15When you are graphing a proportion or a percent, what should you look at to help you understand the bigger picture?.
Answers
Answer:
Or the rate of change. The percentage change.
Slope.
A staircase is
68.7
-feet high and
95.4
-feet at the base. Determine the angle from its base to the top. Round to the nearest tenth of a degree.
Answers
This means that we use the Tangent function.
Since tan(x) = 68.7/95.4
Use the inverse function of ram to solve for x.
tan^1 = (68.7/95.4)
Plug that in to your calculator (make sure it’s in degrees mode)
And you have your answer
Will give brilliant

Answers
Answer:
(6, 4)
Step-by-step explanation:
R(2,4)=(2+4, 4)=(6, 4)
answer
explanation
(6,4)
How should I solve this?

Answers
The parallel sides AB, PQ, and CD, gives similar triangles, ∆ABD ~ ∆PQD and ∆CDB ~ ∆PQB, from which we have;
\( \frac{1}{x} + \frac{1}{y}= \frac{1}{z}\)
Which method can be used to prove the given relation?From the given information, we have;
∆ABD ~ ∆PQD∆CDB ~ ∆PQBAccording to the ratio of corresponding sides of similar triangles, we have;
\( \frac{x}{z} = \mathbf{\frac{BD}{QD} }\)
\( \frac{y}{z} = \frac{BD}{ BQ} \)
Which gives;
\( \mathbf{\frac{y}{z}} = \frac{BD }{ BD - Q D} \)
\( \frac{z}{y} = \frac{BD - QD }{ BD } = 1 - \frac{Q D }{ BD}\)
QD × x = BD × z
BD × z = (1 - QD/BD) × y = y - (QD × y/BD)
Therefore;
BD × z = y - (QD × y/BD)
BQ × y = y - (QD × y/BD)
BQ × y = y - (z × y/x) = y × (1 - z/x)
(1 - z/x) = BQ
BD × z = y × (1 - z/x)
BD = (y × (1 - z/x))/z
Therefore;
QD × x = y × (1 - z/x)
(BD-BQ) × x = y × (1 - z/x)
(BD-(1 - z/x)) × x = y × (1 - z/x)
BD = (y × (1 - z/x))/x + (1 - z/x)
BQ + QD = (1 - z/x) + (y × (1 - z/x))/x
BD = BQ + QD
(y × (1 - z/x))/x + (1 - z/x) = (y × (1 - z/x))/z
(1 - z/x)×(y/x + 1) =(1 - z/x) × y/z
Dividing both sides by (1 - z/x) gives;
y/x + 1 = y/z
Dividing all through by y gives;
(y/x + 1)/y = (y/z)/y
1/x + 1/y = 1/zTherefore;
\( \frac{1}{x} + \frac{1}{y}= \frac{1}{z}\)
Learn more about characteristics similar triangles here:
https://brainly.com/question/1799826
#SPJ1
Direction. Using the data given below, give the corresponding details of the following. Show your solution. B. Using the data from A, make a group frequency distribution. (Note: Cumulative, Relative frequencies must also be present). C. From B, show your solution in getting: a. Number of classes b. Width of interval
Answers
B. The group frequency distribution involves organizing the data into groups or classes and counting the frequency of observations within each class.
To create a group frequency distribution, we need to determine the intervals or classes and count how many data points fall into each interval.
C. a. The number of classes can be determined based on the desired level of detail and the range of the data. To find the number of classes, we can use the square root rule or Sturges' formula.
The square root rule suggests taking the square root of the total number of data points. Sturges' formula recommends using the formula k = 1 + log2(n), where k is the number of classes and n is the total number of data points.
b. The width of each interval can be calculated by dividing the range of the data by the number of classes. The range is the difference between the highest and lowest values in the data set.
Once we have the number of classes and the range, we can divide the range by the number of classes to determine the width of each interval.
It's important to note that without the specific data provided, we cannot provide the exact solution for the number of classes or the width of the interval. These calculations require the actual data points to determine the range and other relevant values.
Learn more about frequency distribution:
brainly.com/question/30371143
#SPJ11
Find the square root of :
√50×8 = ___
Please show steps....
Answers
(c-4) (c-5) Find coefficients
Answers
Step-by-step explanation:
= (c - 4) ( c - 5)
= c ( c- 5 ) -4 (c - 5)
= c² - 5c - 4c + 20
Grouping of like terms since it have already been arranged.
=c² - 9c + 20
since we're finding for the coefficient of c
than we will square both sides or value
given as
\( \sqrt{c {}^{2} } - \sqrt{9c} + \sqrt{20} = 0 \\ c - \sqrt[3]{3c} + \sqrt[2]{10} = 0 \\ c - c + 5 = 0 \\ 0 = 0 - 5 \\ 0 = - 5\)
sorry but I tried.
Write the sentence as an equation.
244 is t increased by 295
Answers
Answer:
244=t+295
Step-by-step explanation:
simplify the equation

Answers
Answer:
D) - 3v³ + 3v²
Step-by-step explanation:
( v³ + v²) + ( 2v² - 4v³)
= v³ + v² + 2v² - 4v³
= - 3v³ + 3v²
A radio transmission tower is 160 feet tall. How long should a guy wire be if it is to be attached 13 feet from the top and is to make an angle of 29\deg with the ground? Give your answer to the nearest tenth of a foot.
Answers
x = 147 / 0.5446 ≈ 270.2 ft
To find the length of the guy wire for a radio transmission tower, trigonometry concepts are applied. Given a tower height of 160 feet, with the wire attached 13 feet from the top and making an angle of 29° with the ground, we can solve for the length of the guy wire, represented by x.
Using the Pythagorean theorem and considering the right triangle formed by the tower height, the wire attachment point, and the ground, we can set up the equation:
x = √((160 - 13)² + x²)
Next, we apply the tangent function to the given angle:
tan(29°) = (160 - 13) / x
Simplifying, we have:
0.5446 = 147 / x
To solve for x, we rearrange the equation:
x = 147 / 0.5446 ≈ 270.2 ft
Rounding to the nearest tenth of a foot, the length of the guy wire required is approximately 270.2 feet. This wire is attached 13 feet from the top of the tower and makes a 29° angle with the ground.
Trigonometry plays a crucial role in solving real-world problems involving angles and distances. It provides a mathematical framework for calculating unknown values based on known information, enabling accurate measurements and constructions.
Learn more about the applications of trigonometry in real-world scenarios:
https://brainly.com/question/31340190
#SPJ11
Which statement about fractions equivalent to One-half is always true?
The numerator is twice the denominator.
The denominator is twice the numerator.
The denominator is equal to the numerator.
The numerator is equal to one less than the denominator.
Answers
X/2X = 1/2
Answer:
B. The denominator is twice the numerator.
Step-by-step explanation:

For each ordered pair determine whether it is a solution to 7x+4y=-23
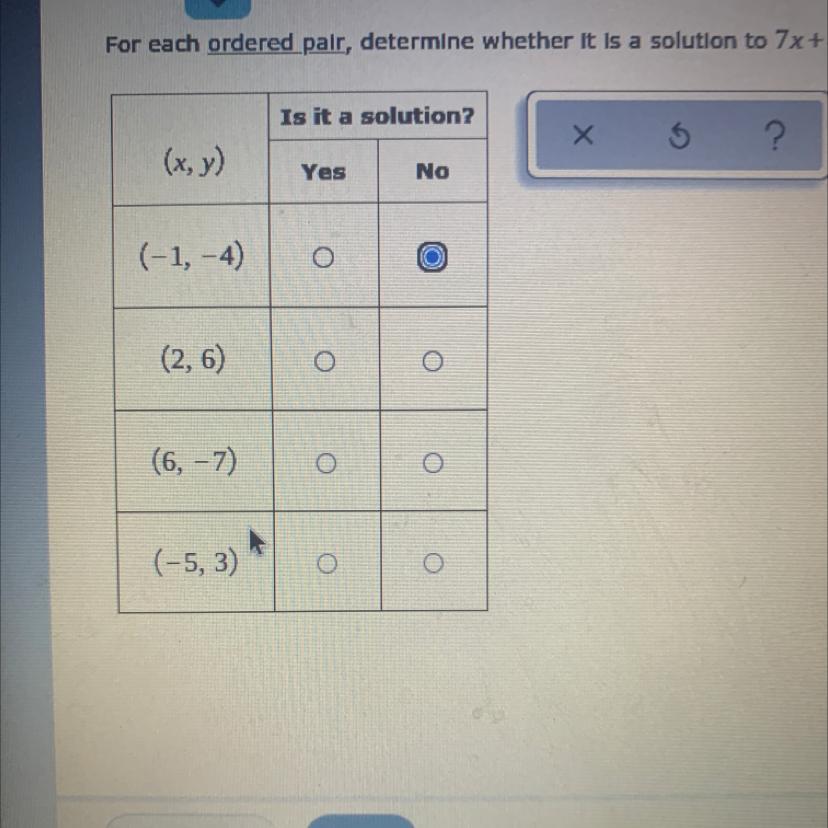
Answers
Answer:
a. no
b. no
c. no
d. yes
Step-by-step explanation:
Case I
x = -1
y = -4
7( -1) + 4 ( -4) = -23
-7 - 4 = -23
- 11 \(\neq\) -23
Case II
x = 2
y= 6
7 (2) + 4 ( 6) = -23
14 + 24 = -23
38 \(\neq\) -23
Case III
x = 6
y = -7
7 ( 6) + 4 (3) =- 23
42+ 12 = -23
54 \(\neq\) -23
Case IV
x = -5
y = 3
7 (-5) + 4 ( 3) =- 23
-35 + 12 = -23
-23 = -23
What is the measure of angle Q and how to solve it?

Answers
The value of the angle Q is 25 degrees
How to determine the valueIt is important to note the following;
The sum of the angles in a triangle is 180 degrees.The sum of angles on a straight line is 180 degrees.From the information given, we have that;
m<P = 90 degrees
m<R = 2x - 5
m<Q = x - 10
Now, equate the angles
m<P +m<R + m< Q = 80 substitute the values
90 + 2x - 5 + x - 10 = 180
collect the like terms
3x = 180 - 75
subtract the values
3x = 105
Divide by the coefficient of x
x = 35
Then, m<Q = 35 - 10 = 25 degrees
Learn more about triangles at: https://brainly.com/question/14285697
#SPJ1
An office manager orders one calculator or one calendar for each of the office's 80 employees. Each calculator costs $12, and each calendar costs $10. The entire order totaled $900.
Part A: Write the system of equations that models this scenario.
Part B: Use substitution method or elimination method to determine the number of calculators and calendars ordered. Show all necessary steps.
Answers
The system of equations is.
x + y = 80
12x + 10y = 900
And the solutions are y = 30 and x = 50
How to write and solve the system of equations?Let's define the two variables:
x = number of calculators.
y = number of calendars.
With the given information we can write two equations, then the system will be:
x + y = 80
12x + 10y = 900
Now let's solve it.
We can isolate x on the first equation to get:
x = 80 - y
Replace that in the other equation to get:
12*(80 - y) + 10y = 900
-2y = 900 - 960
-2y = -60
y = -60/-2 = 30
Then x = 50
Learn more about systems of equations at:
https://brainly.com/question/13729904
#SPJ1
z=1+4i
Find the angle 0(theta) in degrees that z makes in the complex plane.
Round your answer, if necessary, to the nearest tenth. Express 0(theta) between -180 and 180 degrees.
Answers
Answer:
76.0 degrees
Step-by-step explanation:
Just got it right on the Khan Academy quiz.
A cell phone company charges $60 a month for up to 1 gigabyte of data. The cost of additional data is $0.05 per megabyte. If d represents the number of additional megabytes used and c represents the total charges at the end of the month, which linear equation can be used to determine a user's monthly bill?
Answers
Answer:\(c=60+0.05d\)
Step-by-step explanation:
Given
Company charges \(\$60\) for \(1\ GB\) data
and charges \(\$0.05/MB\)
If c is the total cost and d represent no of additional megabyte then
Cost is given by the sum of fixed price + additional data charge
\(c=60+0.05\times d\)
Therefore final charge is given by
\(c=60+0.05d\)
Use the following information to sketch a graph of the original function, f(X) write the equations of any asymptotes. - lim x→[infinity]
f(x)=5 - f ′
(x)>0 on (−2,1)∪(1,[infinity]) - f ′
(x)<0 on (−[infinity],−2) - f ′′
(x)>0 on (−[infinity],−4)∪(1,4) - f ′′
(x)<0 on (−4,−2)∪(−2,1)∪(4,[infinity])
Answers
The equations of the vertical asymptotes can be given as x = -4, -2, and 1. The function f(x) does not have any horizontal asymptotes.
The function, f(x) is given as f(x)=5 - f ′(x)>0 on (−2,1)∪(1,[infinity]) f ′(x)<0 on (−[infinity],−2)f ′′(x)>0 on (−[infinity],−4)∪(1,4)f ′′(x)<0 on (−4,−2)∪(−2,1)∪(4,[infinity])
To sketch the graph of the original function, we have to determine the critical points, intervals of increase and decrease, the local maximum and minimum, and asymptotes of the given function.
Using the given information, we can form the following table of f ′(x) and f ′′(x) for the intervals of the domain.
The derivative is zero at x = -2, 1.
To get the intervals of increase and decrease of the function f(x), we need to test the sign of f ′(x) at the intervals
(−[infinity],−2), (-2,1), and (1,[infinity]).
Here are the results:
f′(x) > 0 on (−2,1)∪(1,[infinity])f ′(x) < 0 on (−[infinity],−2)
As f ′(x) is positive on the intervals (−2,1)∪(1,[infinity]) which means that the function is increasing in these intervals.
While f ′(x) is negative on the interval (−[infinity],−2), which means that the function is decreasing in this interval.
To find the local maximum and minimum, we need to determine the sign of f ′′(x).
f ′′(x)>0 on (−[infinity],−4)∪(1,4)
f ′′(x)<0 on (−4,−2)∪(−2,1)∪(4,[infinity])
We find the inflection points of the function f(x) by equating the second derivative to zero.
f ′′(x) = 0 for x = -4, -2, and 1.
The critical points of the function f(x) are -2 and 1.
The inflection points of the function f(x) are -4, -2, and 1.
Hence, the equations of the vertical asymptotes can be given as x = -4, -2, and 1.The function f(x) does not have any horizontal asymptotes.
Learn more about vertical asymptotes visit:
brainly.com/question/32526892
#SPJ11
Which term has a coefficient of 1?
Answers
Answer:
Variables with no number have a coefficient of 1.
Step-by-step explanation: x is really 1x.
the distance from the ground of a person riding on a ferris wheel can be modeled by the equation d equals 30 times the sine of the quantity pi over 40 times t end quantity plus 20 comma where d represents the distance, in feet, of the person above the ground after t seconds. how long will it take for the ferris wheel to make one revolution? 30 seconds 40 seconds 80 seconds 20 seconds
Answers
The equation given models the distance from the ground of a person riding on a ferris wheel. it takes 80 seconds for the Ferris wheel to make one revolution.
To determine how long it will take for the ferris wheel to make one revolution, we need to find the period of the function. The period is the amount of time it takes for the function to complete one full cycle.
In this case, the function is d = 30sin(pi/40t) + 20, where t is measured in seconds. The period of the function can be found using the formula T = (2pi)/b, where b is the coefficient of t in the argument of the sine function. In this case, b = pi/40, so T = (2pi)/(pi/40) = 80 seconds.
Therefore, it will take 80 seconds for the ferris wheel to make one full revolution. The answer is option C, 80 seconds.
The time it takes for a Ferris wheel to make one revolution can be determined using the given equation: d = 30 * sin((π/40) * t) + 20. In this equation, d represents the distance (in feet) of the person above the ground, and t represents the time in seconds.
A full revolution occurs when the angle inside the sine function completes a cycle of 2π radians. To find the time it takes for this to happen, we need to equate the angle (π/40) * t to 2π:
(π/40) * t = 2π
To solve for t, we can divide both sides of the equation by (π/40):
t = 2π * (40/π)
The π in both the numerator and denominator cancels out:
t = 2 * 40
t = 80 seconds
Therefore, it takes 80 seconds for the Ferris wheel to make one revolution.
Learn more about revolution here
https://brainly.com/question/16533738
#SPJ11
Please help because it my last question

Answers
Answer:
The area of the triangle is 6 units squared.
Step-by-step explanation:
The formula for the area of a triangle is A=1/2B*H. The base in this situation is 4, and the height is 3. 4x3 is 12. We are half 12 because we only need 1/2 of the area, as a triangle is half a square. Thus, our answer is 6 units squared.
Answer:
Step-by-step explanation:
A= 1/2 bh >formula
A= 1/2 (3)(4) >turn triangle so 3 is your base, substitute
A=6
In a sample of 50 iPhones, 13 had over 100 apps downloaded. Construct a 99% confidence interval for the population proportion of all iPhones that obtain over 100 apps. Assume z0.005 = 2.576 .
A. 0.13 ± 0.09
B. 0.26 ± 0.15
C. 0.26 ± 0.16
D. 0.13 ± 0.16
Answers
To construct a confidence interval for the population proportion, we can use the formula:
CI = p ± z * sqrt((p(1 - p))/n)
where p is the sample proportion, z is the z-score corresponding to the desired confidence level, and n is the sample size.
Given:
Sample size (n) = 50
Number of phones with over 100 apps (x) = 13
Desired confidence level = 99%
z-score for a 99% confidence level (z0.005) = 2.576
First, calculate the sample proportion p:
p = x / n
p = 13 / 50
p = 0.26
Next, calculate the margin of error:
ME = z * sqrt((p(1 - p))/n)
ME = 2.576 * sqrt((0.26 * (1 - 0.26))/50)
ME ≈ 0.15
Finally, construct the confidence interval:
CI = p ± ME
CI = 0.26 ± 0.15
Therefore, the 99% confidence interval for the population proportion of phones with over 100 apps is:
Option B: 0.26 ± 0.15
Learn more about confidence interval here : brainly.com/question/29680703
#SPJ11
Jacob took a total of 12 quizzes over the course of 3 weeks.
How many weeks of school will Jacob have to attend this quarter before he will have taken a total of 16 quizzes?
Answers
Answer:
4 weeks
Step-by-step explanation:
The number of weeks for a total of 16 quizzes will be 4 weeks.
What is an expression?
Expression in maths is defined as the collection of the numbers variables and functions by using signs like addition, subtraction, multiplication, and division.
Numbers (constants), variables, operations, functions, brackets, punctuation, and grouping can all be represented by mathematical symbols, which can also be used to indicate the logical syntax's order of operations and other features.
It is given that Jacob took a total of 12 quizzes over the course of 3 weeks. The number of weeks for 16 quizzes will be calculated as below:-
12 quizzes = 3 weeks.
1 quizzes = 3 / 12 weeks
16 quizzes = ( 3 / 12 ) x 16 = 4 weeks
Therefore, the number of weeks for a total of 16 quizzes will be 4 weeks.
To know more about Expression follow
brainly.com/question/723406
#SPJ5