32.725 is it less than or greater than 32.735
Answers
Answer:
Less.
Step-by-step explanation:
Answer:
Less than.
Step-by-step explanation:
Comparing each digit from left to right, the first digit that differs is the hundredths place. 32.725 is less than 32.735.
Related Questions
0.135 written as a fraction is
Answers
Answer:
\( \frac{27}{200} \)Step-by-step explanation:
Convert to a mixed number by placing the numbers to the right of the decimal over 1000. Reduce the fraction.
Hope it is helpful...What is the equation of the line in slope intercept form?

Answers
Answer:
y = x + 60
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
calculate m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (20, 80) and (x₂, y₂ ) = (40, 100) ← 2 points on the line
m = \(\frac{100-80}{40-20}\) = \(\frac{20}{20}\) = 1
the line crosses the y- axis at (0, 60 ) ⇒ c = 60
y = x + 60 ← equation of line
NO LINKS!! URGENT HELP PLEASE!!!
9. Find the equation of the PARABOLA with a vertex at (-2, 6) and passing through the point (1, -3)
Answers
Answer:
y= -x²-4x+2
Step-by-step explanation:
write in vertex form
a(x-h)²+k
in our case h = -2 and k= 6
y=a(x+2)²+6
now we just need to solve for a. we know that when x= 1 y = -3. plug these values in and solve for a
-3= a(1+2)²+6
-9=9a
a= -1
thus the formula is -(x+2)²+6
generally, teachers want things in standard form, so expand the exponent and simplify.
-(x²+4x+4)+6
y= -x²-4x+2
Answer:
\(y = -x^2 - 4x + 2\)
Step-by-step explanation:
The equation of a parabola in vertex form is:
\(y = a(x - h)^2 + k\)
where (h, k) is the vertex of the parabola.
In this case, the vertex is (-2, 6), so h = -2 and k = 6.
We also know that the parabola passes through the point (1, -3).
Plugging these values into the equation, we get:
\(-3 = a(1 - (-2))^2 + 6\)
\(-3 = a(3)^2 + 6\)
-9 = 9a
a = -1
Substituting a = -1 into the equation for a parabola in vertex form, we get the equation of the parabola:
\(y = -1(x + 2)^2 + 6\)
This equation can also be written as:
\(y = -x^2 - 4x -4+6\\y=x^2-4x+2\)
PLEASE, NO LINKS OR FILES. If the diameter of a cylinder is 6 yards, then the value of r 2 is 9 square yards. True False
Answers
Answer:
True
Step-by-step explanation:
Given data
Diameter =6 yards
Radius R= Diameter/2= 6/2 = 3 yards
R²=3*3=9square yards
Hence R^2 = 9square yards= True
Answer:
True.
Step-by-step explanation:
R² is radius to the second power. You were given the diameter, so the radius will be half of that diameter.
3 to the second power, (or 3 x3), is 9.
3n + 6n -4 = 2n + 2 + 5n
Answers
Answer:
3n +6n-4=2n+2+5n
9n-4=7n+2
9n-7n=2+4
2n=6
n=6÷2
n=3
Show that the equations x+y+z = 4, 2x+5y-2z =3, x+7y-7z =5 are not consistent
Answers
Answer:
We can start by using the second equation to eliminate x:
2x + 5y - 2z = 3
2x = -5y + 2z + 3
x = (-5/2)y + z + 3/2
Now we can substitute this expression for x into the first and third equations:
x + y + z = 4
(-5/2)y + z + 3/2 + y + z = 4
(-5/2)y + 2z = 5/2
x + 7y - 7z = 5
(-5/2)y + z + 3/2 + 7y - 7z = 5
(9/2)y - 6z = 7/2
Now we have a system of two equations with two variables, (-5/2)y + 2z = 5/2 and (9/2)y - 6z = 7/2. We can use any method to solve for y and z, such as substitution or elimination. However, we will find that the system is inconsistent, meaning there is no solution that satisfies both equations.
Multiplying the first equation by 9 and the second equation by 5 and adding them, we get:
(-45/2)y + 18z = 45/2
(45/2)y - 30z = 35/2
Adding these two equations, we get:
-12z = 40/2
-12z = 20
z = -5/3
Substituting z = -5/3 into (-5/2)y + 2z = 5/2, we get:
(-5/2)y + 2(-5/3) = 5/2
(-5/2)y - 10/3 = 5/2
(-5/2)y = 25/6
y = -5/12
Substituting y = -5/12 and z = -5/3 into any of the original equations, we get:
x + y + z = 4
x - 5/12 - 5/3 = 4
x = 29/12
Therefore, the solution is (x, y, z) = (29/12, -5/12, -5/3). However, if we substitute these values into any of the original equations, we will find that it does not satisfy the equation. For example:
2x + 5y - 2z = 3
2(29/12) + 5(-5/12) - 2(-5/3) = 3
29/6 - 5/2 + 5/3 ≠ 3
Since there is no solution that satisfies all three equations, the system is inconsistent.
Step-by-step explanation:
Answer:
See below for proof.
Step-by-step explanation:
A system of equations is not consistent when there is no solution or no set of values that satisfies all the equations simultaneously. In other words, the equations are contradictory or incompatible with each other.
Given system of equations:
\(\begin{cases}x+y+z = 4\\2x+5y-2z =3\\x+7y-7z =5\end{cases}\)
Rearrange the first equation to isolate x:
\(x=4-y-z\)
Substitute this into the second equation to eliminate the term in x:
\(\begin{aligned}2x+5y-2z&=3\\2(4-y-z)+5y-2z&=3\\8-2y-2z+5y-2z&=3\\-2y-2z+5y-2z&=-5\\5y-2y-2z-2z&=-5\\3y-4z&=-5\end{aligned}\)
Subtract the first equation from the third equation to eliminate x:
\(\begin{array}{cccrcrcl}&x&+&7y&-&7z&=&5\\\vphantom{\dfrac12}-&(x&+&y&+&z&=&4)\\\cline{2-8}\vphantom{\dfrac12}&&&6y&-&8z&=&1\end{aligned}\)
Now we have two equations in terms of the variables y and z:
\(\begin{cases}3y-4z=-5\\6y-8z=1\end{cases}\)
Multiply the first equation by 2 so that the coefficients of the variables of both equations are the same:
\(\begin{cases}6y-8z=-10\\6y-8z=1\end{cases}\)
Comparing the two equations, we can see that the coefficients of the y and z variables are the same, but the numbers they equate to is different. This means that there is no way to add or subtract the equations to eliminate one of the variables.
For example, if we subtract the second equation from the first equation we get:
\(\begin{array}{crcrcl}&6y&-&8z&=&-10\\\vphantom{\dfrac12}-&(6y&-&8z&=&\:\:\;\;\:1)\\\cline{2-6}\vphantom{\dfrac12}&&&0&=&-11\end{aligned}\)
Zero does not equal negative 11.
Since we cannot eliminate the variable y or z, we cannot find a unique solution that satisfies all three equations simultaneously. Therefore, the system of equations is inconsistent.
1.What is the equation of a circle with center (-2, 2) and radius 3?
Answers
Answer:
(x + 2)² + (y - 2)² = 3²
Step-by-step explanation:
Equation of a circle is (x - a)² + (y - b)² = r²,
where a is the x-coordinate of the centre of the circle, b is the y-coordinate of the centre of the circle, r is the circle's radius.
So, we have (x - -2)² + (y - 2)² = 3²
subtract a minus means we add.
(x + 2)² + (y - 2)² = 3²
I’m am so lost please help thank you all

Answers
Answer:
Step-by-step explanation:
148 people
In the figure, ABCD and DEFG are squares. AC:FD=7:5, find CE(English isn't my native language. Please correct me if I have any grammatical mistakes.)

Answers
The diagonal ratio is given AC:FD=7:5.
The length of AG is 3cm.
ExplanationTo find CE.
The diagonals ratio is same as the side of square ratio.
Reason-
The diagonals are the square root of 2 multiply by side.
\(D=\sqrt{2}S\)D denotes the diagonal and S denote the side, of suare.
So, the ratio of diagonal is same as the ratio of sides of square.
\(\frac{D}{d}=\frac{S}{s}\)Here D and d denotes the diagonal of the squares and s and S is the sides of squares.
Let AD = 7x , GD = 5x
\(\begin{gathered} AG=AD-GD \\ 3=7x-5x \\ 3=2x \\ x=1.5 \end{gathered}\)Now find the length of CE,
\(\begin{gathered} CE=CD+DE \\ CE=7x+5x \\ CE=12x \end{gathered}\)Substitute the value of x in the CE.
\(\begin{gathered} CE=12\times1.5 \\ CE=18cm \end{gathered}\)AnswerHence thelenghth CE is 18cm.
2. The diagram above shows a wooden structure in the form of a cone mounted on hemispherical base. The vertical height of the cone is 24cm and the base 7cm. Calculate correct to 3 significant figures the surface area of the structure. (Take π= 22/7)
Answers
The surface area of the wooden structure is approximately 1012 cm².
To calculate the surface area of the wooden structure, we need to find the surface area of the cone and the surface area of the hemispherical base, and then add them together.
Surface Area of the Cone:
The surface area of a cone is given by the formula:
A_{cone = \(\pi \times r_{cone} \times (r_{cone} + s_{cone})\), \(r_{cone\) is the radius of the base of the cone and \(s_{cone\) is the slant height of the cone.
The vertical height of the cone is 24 cm, and the base radius is 7 cm, we can calculate the slant height using the Pythagorean theorem:
\(s_{cone\) = \(\sqrt{(r_{cone}^2 + h_{cone}^2).\)
Using the given measurements:
\(s_{cone\) = √(7² + 24²) cm
\(s_{cone\) ≈ √(49 + 576) cm
\(s_{cone\) ≈ √625 cm
\(s_{cone\) ≈ 25 cm
Now, we can calculate the surface area of the cone:
\(A_{cone\) = π × 7 cm × (7 cm + 25 cm)
\(A_{cone\) = (22/7) × 7 cm × 32 cm
\(A_{cone\) = 704 cm²
Surface Area of the Hemispherical Base:
The surface area of a hemisphere is given by the formula:
\(A_{hemisphere\) = \(2 \times \pi \times r_{base}^2\), \(r_{base\) is the radius of the base of the hemisphere.
Given that the base radius is 7 cm, we can calculate the surface area of the hemispherical base:
\(A_{hemisphere\) = 2 × (22/7) × (7 cm)²
\(A_{hemisphere\) = (22/7) × 2 × 49 cm²
\(A_{hemisphere\) = 308 cm²
Total Surface Area:
To calculate the total surface area, we add the surface area of the cone and the surface area of the hemispherical base:
Total Surface Area = \(A_{cone} + A_{hemisphere}\)
Total Surface Area = 704 cm² + 308 cm²
Total Surface Area = 1012 cm²
For similar questions on surface area
https://brainly.com/question/16519513
#SPJ8
One fourth of a number and two is three in equation form.
Answers
Answer:
1/4x+2=3
Step-by-step explanation:
hopefully this helps :)
Evaluate and input the result of the following integral.
∫ Fdr= ?
c
F=
Answers
Answer:
∫ F dr= 1
c
Step-by-step explanation:
The correct question is -
Given - \(F = < \frac{sec^{2} x}{y} , - \frac{tan x}{y^{2} }>\) and C : (0, 1) to \((\frac{\pi }{4} , 1)\)
To find - Evaluate and input the result of the following integral.
Proof -
We know that,
dr = dx i + dy j
F = < F1, F2 >
Now, we know
\(d(\frac{tanx}{y }) = \frac{d}{dx}(\frac{tanx}{y}) + \frac{d}{dy}(\frac{tanx}{y})\)
So,
\(\frac{d}{dx}(\frac{tanx}{y}) =\frac{1}{y} \frac{d}{dx}({tanx}) \\\\ = \frac{sec^{2} x}{y} \\\frac{d}{dy}(\frac{tanx}{y}) = tanx \frac{d}{dy}(y^{-1}) \\ = -\frac{tanx}{y^{2} }\)
Now,
We can see that,
\(d(\frac{tanx}{y }) = \frac{sec^{2} x}{y} dx - (\frac{tanx}{y^{2} })dy\)
So,
\(\int\limits^{}_C {F. dr} = \int\limits^{}_C d(\frac{tanx}{y} )\\= [\frac{tanx}{y} ]\limits^{(\frac{\pi }{4} ,1)}_{(0,1)}\\= [\frac{tanx}{y} ]\limits^{}_{(\frac{\pi }{4} ,1)} - [\frac{tanx}{y} ]\limits^{}_{(0,1)}\\= \frac{tan(\frac{\pi }{4} )}{1} - \frac{tan 0}{1}\\= 1 - 0\\= 1\)
∴ we get
∫ F dr= 1
c

why do the hands on the clock form an angle?
Answers
Answer:
The entire clock measures 360 degrees. As the clock is divided into 12 sections. The distance between each number is equivalent to 30 degrees (360/12)
I hope this helps you!
1. Decide whether each of the following descriptions most closely corresponds to being part of a command system, a market system, or a laissez-faire system.
a. A woman who wants to start a flower shop finds she cannot do so unless the central government has already decided to allow a flower shop in her area.
b. Shops stock and sell the goods their customers want but the government levies a sales tax on each transaction in order to fund elementary schools, public libraries, and welfare programs for the poor.
c. The only taxes levied by the government are to pay for national defense, law enforcement, and a legal system designed to enforce contracts between private citizens.
Answers
The best representations of each of the given situation are as follows;
a). A woman who wants to start a flower shop finds she cannot do so unless the central government has already decided to allow a flower shop in her area. - A market system.
b). Shops stock and sell the goods their customers want but the government levies a sales tax on each transaction in order to fund elementary schools, public libraries, and welfare programs for the poor. - A command system.
c). The only taxes levied by the government are to pay for national defense, law enforcement, and a legal system designed to enforce contracts between private citizens. - A laissez-faire system.
What is a laissez-faire system?Laissez-faire system economics is a theory which postulates that the government should not intervene in the economy except to protect individuals' inalienable rights.
Read more on laissez-faire system;
https://brainly.com/question/21321460
#SPJ1
50 POINTS and BRAINLIEST-- A pattern of shaded and unshaded squares is shown below:

Answers
Answer:
The number of shaded squares changes by 2 in each figure
Therer will be 90 squares shaded in the 50th figure
Step-by-step explanation:
Brainliest PLS

Answer:
1. I'm not exactly sure but I would say that you add two to every square.
2. 90
Step-by-step explanation:
To find the first answer, you just add and count the squares.
To find the second answer, you just add two to every square, up to 50 squares.
Right triangle QRS is pictured below.

Answers
Step-by-step explanation:
Step 1: List out all of the formulas for the trigonometric functions
sin(x) = opposite/hypotenuse
cos(x) = adjacent/hypotenuse
tan(x) = opposite/adjacent
Step 2: Find the value of RS
cos(31) = RS/24.8 NOT 24.8/RS
sin(31) = QS/24.8 NOT RS/24.8
sin(31) = QS/24.8 NOT 24.8/RS
cos(31) = RS/24.8 WHICH IS SAME AS RS/24.8
Answer: The correct length would be given from Option D, cos(31) = RS/24.8
Answer:the answer is a
Step-by-step explanation:
Marty paid $45 for a jacket that had been marked down 25%. What is the original price of the jacket?
Answers
Answer:
11.25
Step-by-step explanation:
You get the 45 dollars then you do 0.45 then you times it by 25
Answer:
180
Step-by-step explanation:
25%-.25
45/.25
180
Which expression is equivalent to "9 more than the quotient of x and 5
Answers
The required expression is (x / 5) + 9
Given that we have to build an equation for the statement "9 more than the quotient of x and 5,
So,
This expression represents the quotient of x divided by 5, and then adding 9 to the result.
Therefore,
"9 more than the quotient of x and 5" can be written mathematically as:
(x / 5) + 9
Hence the required expression is (x / 5) + 9
Learn more about expression click;
https://brainly.com/question/15994491
#SPJ1
An increase from $27 to $35.10 what percent of increase?
Answers
Answer:
30% increase
Step-by-step explanation:
percentage increase is calculated as
\(\frac{increase}{original}\) × 100%
increase = $35.10 - $27 = $8.10 , then
percentage increase = \(\frac{8.10}{27}\) × 100% = 0.3 × 100% = 30%
Answer:
Step-by-step explanation:
step 1: 35.10-27 =8.1
step 2: 8.1/27 x 100 = 30%
so therefore = 30% increase
The figures below are scaled copies. Identify the corresponding parts.

Answers
Answer:
a. ∠U
b. ∠D
c. WX
d. ST
Step-by-step explanation:
The line segment joining the points P(-3,2) and Q(5,7) is divided by the y-axis in the ratio:
Answers
Answer:
Step-by-step explanation:
The line segment joining two points P and Q can be represented by the equation of a straight line in the form y = mx + b, where m is the slope and b is the y-intercept.
To find the equation of the line, we need to find the slope, which can be calculated using the formula:
m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of the points P and Q, respectively.
In this case, the coordinates are:
P = (-3, 2) and Q = (5, 7)
So, the slope is:
m = (7 - 2) / (5 - (-3)) = 5 / 8
Next, we can use either of the points to find the y-intercept. Let's use point P:
b = y - mx, where y and x are the y and x coordinate of the point, respectively.
In this case,
b = 2 - m * (-3) = 2 - (5/8) * (-3) = 2 + 15/8 = 89/8
So, the equation of the line joining the points P and Q is:
y = (5/8)x + 89/8
Now, to find the point where the line crosses the y-axis, we need to find the x-coordinate of the point where y = 0.
So, we have:
0 = (5/8)x + 89/8
Solving for x, we get:
x = -(89/8) / (5/8) = -89 / 5
This means that the line crosses the y-axis at the point (-89/5, 0). To find the ratio in which the line segment is divided by the y-axis, we need to find the ratio of the distance from the y-axis to point P to the distance from the y-axis to point Q.
Let's call the point of intersection with the y-axis R. The distances are then:
PR = (3, 2) and QR = (5 - (-89/5), 7)
The ratio of the distances is then:
PR / QR = (3, 2) / (5 - (-89/5), 7) = 3 / (5 + 89/5) = 3 / (94/5) = 15/47
So, the line segment joining the points P and Q is divided by the y-axis in the ratio 15:47.
What is 35 degree angle in standard position?

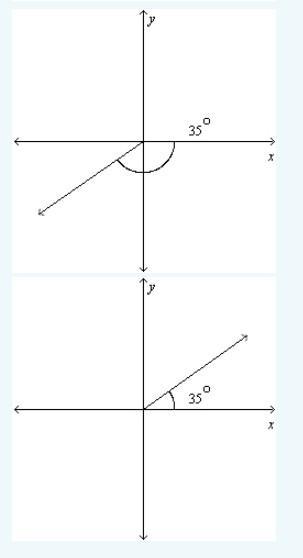
Answers
After using ruler and following the steps described below
We get the standard position of 35 degree.
The given angle is = 35 degree
To draw standard position of angle:
We proceed it to draw by ruler
So, in order to get position,
Follow the following steps:
1: Draw a straight line with your ruler.
2: Place your protractor on the line and align the base of the protractor with the line.
3: Find the 35 degree mark on the protractor and make a small mark on the line at that point.
4: Move your protractor to the mark you just made.
5: Align the base of the protractor with the line and make another small mark on the line at the 35 degree mark.
6: Draw a straight line connecting the two points you just marked.
And there you have it! A 35 degree angle drawn on paper.
And after following these steps we get the standard potion angle 35 degree.
Learn more about the angle visit:;
https://brainly.com/question/25716982d
#SPJ1

Find the measure of the indicated angles.
complementary angles with measures 2x - 2 and 5x – 13
Answers
Answer:
1st angle is 28° and the 2nd angle is 62°
Step-by-step explanation:
Complementary angles mean that the angles add up to 90 so:
2x - 2 + 5x - 13 = 90
7x - 15 = 90
7x = 90 + 15
7x = 105
x = 15
Plugging in:
2x - 2
2(15) - 2
30 - 2
28
5x - 13
5(15) - 13
75 - 13
62
Fill in the blank to complete the sentence. A square with area 49 cm² has perimeter cm ok 2 Asquare with area 49 cm? has perimeter (cm] (Type a whole number.)
Answers
Answer:
7 cm
Step-by-step explanation:
it is a square so sqrt(49)=7, and the side lengths are 7
What is 0.62x10 yo the power of 3
Answers
Answer:
62
Step-by-step explanation:
Answer:
238.328
Step-by-step explanation:
The product of 0.62 x 10 is 6.2. So, I did 6.2 to the power of 3, which is 238.328.
Can someone help me with this problem?

Answers
7. Radius of circle P = 2 Radius of circle Q = 1
Coordinates of the point of tangency (4,2)
The equation of the tangency line is x = 4
8. AB is not a tangent. BC² ≠ AB² + AC²
9. The three radii of the circle are; CB, CF and CD
A diameter of the circle is BD
A tangent of the circle is GE
A chord of the circle is BD
A secant of the circle is AD
A point of tangency is F
How do we find the radius of a circle?
7. To find the radius, identify the diameter of the circle. For the diagram, it can be said that the diameter of the circle P is 4.
The radius then is 4/2 = 2.
The radius of circle q is 2/2 = 1
You could also use the formula
Distance = sqrt((x2 - x1)² + (y2 - y1)²)
8. √4² + √12² = √160
√13 = 169
Therefore AB is not tangent. It is less than BC
9. The line that cuts the circle into two halves is the diameter. The lines than further cuts the diameter into equal parts are the radii's
Find more exercises on finding diameter and radius;
https://brainly.com/question/23891151
#SPJ1
What is the equation of line b d, simplified? y − y1 = m(x − x1) y − 0 = (startfraction 2 b over 2 a minus c endfraction)(x − c) y = (startfraction b over a minus c endfraction)x − (startfraction 2 b c over 2 a minus c endfraction) y = (startfraction 2 b over 2 a minus c endfraction)x − (startfraction b c over 2 a minus 2 c endfraction) y = (startfraction 2 b over 2 a minus c endfraction)x − (startfraction 2 b c over 2 a minus c endfraction) y = (startfraction 2 b over a minus c endfraction)x − (startfraction 2 b c over a minus c endfraction)
Answers
The required equation of line BD is option d.) \(y=\frac{2b}{2a-c} x-\frac{2b}{2a-c} c\)
Equation of the line is given be in standard form is
\(y-y_{1} =\frac{y_2-y_1}{x_2-x_1} (x-x_1)\)
Line, curve of the shortest distance between two points.
The questions seem to be incomplete the question, the complete question could be
a)\(y=\frac{2b}{2a-c} (x-c)\\\)
b)\(y=\frac{b}{-c} x-\frac{2b}{2a-c}\)
c)\(y=\frac{2b}{2a-c} x-\frac{bc}{2a-2c}\)
d)\(y=\frac{2b}{2a-c} x-\frac{2b}{2a-c} c\)
e)\(y=\frac{2b}{a-c} x-\frac{2b}{a-c}\)
Now all the Equation in option represents the triangle with coordinates A(0, 0), B (2a, 2b), C(2c,0) and D(c, 0).
For equation of line BD we have coordinates, (2a, 2b) and (c, 0).
putting these coordinates in the standard form of equation of line i.e.
\(y-y_{1} =\frac{y_2-y_1}{x_2-x_1} (x-x_1)\)
⇒ \(y=\frac{2b}{2a-c} x-\frac{2b}{2a-c} c\)
Thus the required equation of the line is \(y=\frac{2b}{2a-c} x-\frac{2b}{2a-c} c\).
learn more about line here:
brainly.com/question/2696693
#SPJ1
Answer:
C
Step-by-step explanation:
Edg
A bagel shop sells coffee in a container shaped like a rectangular prism. A graphic designer who works for the bagel shop drew the net below to create a design for the container.
Answers
1598 cm square is the area of the container.
According to the statement
we have given that the container is rectangular prism
And Length of rectangular prism is 34cm
Width of rectangular prism is 17 cm
Height of rectangular prism is 20 cm
we use the below written formula to find the surface area
Surface area formula A=(wl+hl+hw)
To find the surface area of the container.
Substitute the values of Length, width and height in the formula then
A=(wl+hl+hw)
A=((17)(34)+(20)(34)+(20)(17))
After solving the values
A=(578+680+340)
A= 1598
So, 1598 cm square is the area of the container.
Learn more about AREA here https://brainly.com/question/6613758
#SPJ1
Geometry question. Please help fast.

Answers
The correct answers are 1st and 4th i.e translate 2 units down and reflect the triangle.
We can easily deduce that the triangle A'B'C' is 2 units higher than the triangle ABC so if we want to map the both the triangles we have to make the triangle A'B'C' lower in the graph.
So, both the 1st and 4th points translate and reflect down the triangle A'B'C' which will be mapped according to the triangle ABC.
To know about more translate and reflect https://brainly.com/question/12381163
#SPJ1
The graph shows the number of books, y, Melissa read during the weeks of summer break, x. She also read several books during the school year.
Determine the equation that can be used to represent this situation.
y = 3x
y = x + 5
y = 3x + 15
y = x + 15
Answers
Answer:
Step-by-step explanation:
Y=3x+15

Answer:
3x+15
Step-by-step explanation:
3x+15