8 2 Solve y' = Ay, where -6 24 (1) A= -1 8 4 2 -12 -6 and y(1) = [1]
Answers
The required answer is y(t) = | 4t(2t + 8t^2 + 2t^3) | .
Explanation:-
To solve the differential equation y' = Ay, where A is the given matrix and y(1) = [1], use the matrix exponential method. The solution can be written as y(t) = e^(At) * y(0), where e^(At) represents the matrix exponential and y(0) is the initial condition vector.
First, to find the matrix exponential e^(At). To calculate this, use the power series expansion of the exponential function:
e^(At) = I + At + (At)^2/2! + (At)^3/3! + ...
To obtain e^(At),to calculate the powers of A multiplied by t. start by calculating A^2:
A^2 = A * A =
|-6 24 | |-6 24 | | -12 48 |
| 1 -8 | * | 4 2 | = | -4 -2 |
| 4 2 | | -12 -6 | | 16 4 |
Next, calculate A^3:
A^3 = A * A^2 =
|-6 24 | |-6 24 | | 48 240 |
| 1 -8 | * | -4 -2 | = | 0 -16 |
| 4 2 | | 16 4 | | 8 32 |
Now calculate e^(At) using the power series expansion:
e^(At) ≈ I + At + (At)^2/2! + (At)^3/3! + ...
I is the identity matrix of the same size as A. In this case, it is a 3x3 matrix with ones on the diagonal and zeros elsewhere:
I =
| 1 0 0 |
| 0 1 0 |
| 0 0 1 |
Now substitute the values of A, A^2, and A^3 into the power series expansion:
e^(At) ≈ I + At + (At)^2/2! + (At)^3/3!
e^(At) ≈
| 1 0 0 | + t |-6 24 | + t^2 | -12 48 | /2! + t^3 | 48 240 | /3!
| 0 1 0 | | 1 -8 | | -4 -2 | | 0 -16 |
| 0 0 1 | | 4 2 | | 16 4 | | 8 32 |
calculate the matrix exponential:
e^(At) ≈| 1 - 6t + 6t^2 - 2t^3 24t - 48t^2 + 24t^3 |
=| t 1 - 8t + 4t^2 |
=| 4t 2t + 8t^2 + 2t^3 |
Now find the solution y(t) by multiplying e^(At) with the initial condition y(0):
y(t) = e^(At) * y(0) =
| 1 - 6t + 6t^2 - 2t^3 24t - 48t^2 + 24t^3 | * | 1 |
| t 1 - 8t + 4t^2 | | 0 |
| 4t 2t + 8t^2 + 2t^3 | | 1 |
Simplifying the multiplication, we get:
y(t) =| 1 - 6t + 6t^2 - 2t^3 + 24t - 48t^2 + 24t^3 |
= | t(1 - 8t + 4t^2) |
= | 4t(2t + 8t^2 + 2t^3) |
Now substitute t = 1 to find the particular solution that satisfies the initial condition y(1) = [1]:
y(1) =| 1 - 6(1) + 6(1)^2 - 2(1)^3 + 24(1) - 48(1)^2 + 24(1)^3 |
=| 1(1 - 8(1) + 4(1)^2) |
=4(1)(2(1) + 8(1)^2 + 2(1)^3) |
Simplifying further,
y(1) =| 1 - 6 + 6 - 2 + 24 - 48 + 24 |
=| 1 - 8 + 4 |
=| 8 + 16 |
y(1) =| -1 |
=| -3 |
=| 24 |
Therefore, the solution to the differential equation y' = Ay with the initial condition y(1) = [1] is:
y(t) = | 1 - 6t + 6t^2 - 2t^3 + 24t - 48t^2 + 24t^3 |
y(t) = | t(1 - 8t + 4t^2) |
y(t) = | 4t(2t + 8t^2 + 2t^3) |
Substituting t = 1, we have:
y(1) =| -1 |
=| -3 |
=| 24 |.
To know about exponential function . To click the link.
https://brainly.com/question/29287497.
#SPJ11
Related Questions
11 points given
The net of a cuboid, with one face missing, is shown below. a) What are the dimensions of the missing face? b) Which four edges could the missing face be attached to? H 8 cm G A B F 5 cm C 10 cm E D Not drawn accurately
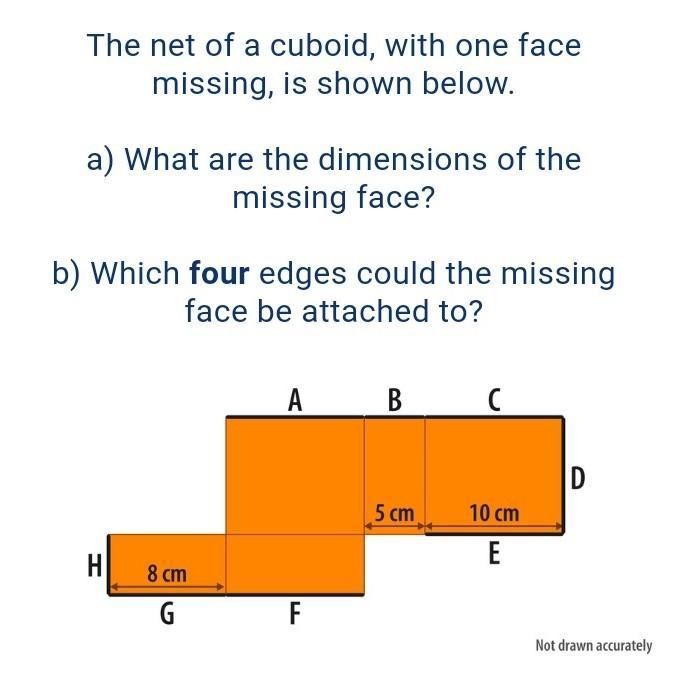
Answers
a) The dimensions of the missing face is 10 x 5 cm.
b) The four edges that the missing face can be attached are: A, B, C and H.
What is a net of a shape?The net of a given shape is the figure formed when all its surfaces are spread out on a 2 dimensional plane. The shape is reproduced when the net is folded as require.
A cuboid if a 3 dimensional shape that is produced from a rectangle. Such that it has length, width and height.
In the given net of a cuboid, it can be deduced that;
a. The dimension of the missing face is that similar to F, such that it is 10 x 5 cm.
b. The four edges that the missing face could be attached to should be A, B, C and H. This is the closed end of the cuboid.
Learn more about the net of a shape at https://brainly.com/question/21001813
#SPJ1
Explain why the product of 4 x 500 has three Os, not just two Os.
Answers
Answer:
because 4 is being multiplied by 500 which has two zeros because it is a multiple of 100
Step-by-step explanation:
Answer:
Because when you multiply 500 by 4 you start with the first 0. 4x0 is 0, now you move on to the second 0. 4x0 is 0, so that one is 0 too. Now you multiply the 5. 5x4 is 20. You put the 20 first, followed by the two 0s, And you get 2,000.
Step-by-step explanation:
pls help i have been busy doing my other homeworks

Answers
Answer:
Step-by-step explanation:
1. 39
2. 141
3. 39
4. 141
5. 141
6. 39
7. 141
8. 39
9. 39
10. 141
11. 141
12. 39
13. 39
14. 141
15. 141
16. 39
Let x and y be real numbers such that x < 2y. Prove that if
7xy ⤠3x2 + 2y2, then 3x ⤠y.
Answers
To prove that 3x ≤ y, assume the opposite, that is, 3x > y, rearrange the inequality substitute x < 2y and simplify, contradict the given condition that x < 2y, therefore, concluding that 3x ≤ y.
Start by assuming the opposite, that is, 3x > y.
From the given inequality,\(7xy \leq 3x^2 + 2y^2,\), we can rearrange to get:
\(7xy - 3x^2 \leq 2y^2\)
We can substitute \(x < 2y\) into this inequality:
\(7(2y)x - 3(2y)^2 \leq 2y^2\)
Simplifying, we get:
\(y(14x - 12y) \leq 0\)
Since y is a real number, this means that either y ≤ 0 or 14x - 12y ≤ 0.
If y ≤ 0, then 3x ≤ y is trivially true.
If 14x - 12y ≤ 0, then we can rearrange to get:
3x ≤ (12/14)y
3x ≤ (6/7)y
3x < y (since we assumed 3x > y)
But this contradicts the given condition that x < 2y, so our assumption that 3x > y must be false.
Therefore, we can conclude that 3x ≤ y.
Know more about inequality here:
https://brainly.com/question/25275758
#SPJ11
This is an example of an Undamped Forced Oscillation where the phenomenon of Beats Occurs.
Find the solution of the initial value problem:
x ′′ +33.64x=4cos(6t), x(0)=x ′ (0)=0
x(t)=
Answers
The solution of the given initial value problem, x'' + 33.64x = 4cos(6t), with x(0) = x'(0) = 0, can be expressed as a sum of the homogeneous solution and the particular solution.
To find the solution, we start by solving the homogeneous equation, x'' + 33.64x = 0. The characteristic equation associated with this homogeneous equation is \(r^2 + 33.64 = 0\), which yields the roots
r = ±i√33.64. Thus, the homogeneous solution can be expressed as
x_h(t) = A*cos(√33.64*t) + B*sin(√33.64*t),
where A and B are constants determined by the initial conditions.
Next, we need to find the particular solution for the forced oscillation. Since the right-hand side of the equation is of the form Acos(ωt), where ω = 6, we assume a particular solution of the form x_p(t) = C*cos(ω*t + φ), where C and φ are constants to be determined. Taking the derivatives, we have x_p''(t) = -ω^2*C*cos(ω*t + φ) and x_p'(t) = -ω*C*sin(ω*t + φ). Substituting these into the original equation, we obtain -ω^2*C*cos(ω*t + φ) + 33.64*C*cos(ω*t + φ) = 4*cos(ω*t).
To satisfy this equation, the coefficient of the cosine term must be 4, while the coefficient of the sine term must be zero. This gives us two equations: -ω^2*C + 33.64*C = 4 and -ω*C = 0. Solving these equations, we find C = 4/(33.64 - ω^2) and φ = 0. Therefore, the particular solution is x_p(t) = (4/(33.64 - ω^2))*cos(ω*t).
Finally, we combine the homogeneous solution and the particular solution to obtain the complete solution:
x(t) = x_h(t) + x_p(t) = A*cos(√33.64*t) + B*sin(√33.64*t) + (4/(33.64 - ω^2))*cos(ω*t).
By substituting the initial conditions x(0) = x'(0) = 0 into this equation, we can determine the values of A and B. With the obtained values, the final solution for the initial value problem can be expressed in terms of the given constants and the trigonometric functions involved.
Learn more about trigonometric functions here: https://brainly.com/question/25618616
#SPJ11
A. No, because one x-value corresponds to two different y-values.
B. Yes, because there are two x-values that are the same.
C. No, because two of the y-values are the same.
D. Yes, because every x-value corresponds to exactly one y-value.

Answers
Answer:
its A
Step-by-step explanation:
:)
It snowed 7.29 inches on Monday and 0.78 inches on Tuesday. How much did it snow on
Monday and Tuesday combined?
Answers
Answer:
8.07 inches
Step-by-step explanation:
7.29+0.78=8.07
I really need help to get this done, please.

Answers
Answer:
The area of the base of the cylinder (the circle face) is the same as the area of the base of the prism (the triangle face).
Step-by-step explanation:
The volume of a prism is the area of the base of the prism multiplied by its height.
The volume of a cylinder is the area of the base of the cylinder multiplied by its height.
So because the volumes are both equal, and the heights are both equal
Then the area of the bases should also be equal.
This will need to be your heading for Question 4. A bond with 26-year maturity was issued 6 years ago. The face value of this 8.1% semi-annual coupon paying bond is $4,000. Analysts find that the current yield to maturity of this bond is 14.62 percent. Show your workings and find the value of this bond. Compare this value against the face value of the bond and write your comment to explain the difference, if any. (Use max 100 words for the explanation).
Answers
The difference between the face value ($4,000) and the calculated value ($3,094.59) of the bond is due to the difference in the current yield to maturity and the coupon rate.
To find the value of the bond, we can use the formula for the present value of a bond:
Bond Value = (Coupon Payment / \((1 + Yield/2)^(2n))\) + (Face Value / (1 + \(Yield/2)^(2n))\)
Where:
Coupon Payment = (8.1% / 2) * Face Value
Yield = 14.62% (expressed as a decimal)
n = number of coupon periods remaining = (26 - 6) * 2
Plugging in the values, we get:
Coupon Payment = (8.1% / 2) * $4,000 = $162
n = (26 - 6) * 2 = 40
Using a financial calculator or spreadsheet, we can calculate the present value of the bond to be $3,094.59.
The difference between the face value ($4,000) and the calculated value ($3,094.59) of the bond is due to the difference in the current yield to maturity and the coupon rate.
Learn more about statistics here:
https://brainly.com/question/30915447
#SPJ11
Which scale can she use for the vertical axis such that the difference in the heights of the bars is maximized
Answers
The scale that a person can use for the vertical axis such that the difference in the heights of the bars is maximized is called Logarithmic Scale.
Logarithmic Scale: It is used when the data covers a large range of values, as it allows for a more precise representation of the data.
It compresses the data so that the graph can fit on a single page.
The logarithmic scale has a logarithmic base, which is often 10 or e.
The tick marks and labels on a logarithmic scale aren't evenly distributed; instead, they're spaced according to the logarithm of their values.
The logarithmic scale, also known as the log scale, is a scale that measures values logarithmically rather than linearly.
A logarithmic scale is commonly used in scientific and engineering graphs and charts. It is used for data that covers a large range of values, such as population growth, global warming, and the stock market.
Summary:Therefore, the scale that a person can use for the vertical axis such that the difference in the heights of the bars is maximized is called Logarithmic Scale.
Learn more about Logarithmic Scale click here:
https://brainly.com/question/30188637
#SPJ11
Can I get some help with this question please?

Answers
Answer:
g would be 130 because it's a vertical angle with the 130 angle. h is 50 because it has to complement the 130 angle.
K is 74 because it's a vertical angle with the 74 angle, and m is 106 because it needs to complement with k.
In a survey of 1316 people, 926 people said they voted in a recent presidential election. Voting records show that 68% of eligible voters actually did vote. Given that 68% of eligible voters actually did vote, find the probability that among 1316 randomly selected voters, at least 926 actually did vote, then determine what the results suggest.
Answers
The correct option is,
⇒ Some people are being less than honest because P (x ≥ 0.26) is less than 5%.
We have to given that,
In a survey of 1316 people, 926 people said they voted in a recent presidential election. Voting records show that 68% of eligible voters actually did vote.
And, 68% of eligible voters actually did vote.
We can used the formula,
z = √n (p' - p) / √p(1-p)
Substitute all the values, we get;
z = √1316 (925.5/1316 - 0.68) / √0.68 (1 - 0.68)
z = 1.80
Hence, The probability that among 1316 randomly selected voters, at least 926 actually did vote is,
P (X ≥ 926) = P (Z ≥ 1.809..) = 0.035 < 0.05
Therefore, The correct option is B.
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ4
PLS HELP
A sand castle can be modeled with four 6-inch-tall square prisms, one on top of the other, as shown in the figure below.
The base of the bottom prism has a side length of 30 inches, and the base of each of the other three prisms has a side length 7 inches less than the side length of the base of the prism below it. What is the volume of the sand castle?
5,196 square inches
7,422 square inches
10,596 square inches
Answers
Answer:
10,596 cubic inches
Step-by-step explanation:
The shape of the prism with which the sand castle can be modelled = Square prism
The arrangement of the square prism = One on top of the other
The given height of each prism, h = 6 inches
The side length of the base of the bottom prism, s₄ = 30 inches
The side length of the base of the other prism = The side length of the base of the prism below each prism - 7 inches
Therefore;
The side length of a prism = 7 inches + The side length of the prism above it
Given that the side length of the base prism (The fourth prism), s₄ = 30 inches
The side length of the prism, directly above the base prism (The fourth prism), s₃ = (30 - 7) inches = 23 inches
The side length of the prism, directly above the third prism (The second prism), s₃ = (23 - 7) = 16 inches
The side length of the top most prism, s₁ = (16 - 7) inches = 9 inches
The volume of the sand castle, V = h × (s₄² + s₃² + s₂² + s₁²)
∴ V = 6 × (30² + 23² + 16² + 9²) = 10,596
The volume of the sand castle, V = 10,596 in.³
Heyo!
The volume of the sandcastle above is 10,596 cubic inches.
Hope this helps! If so, please lmk! Tysm and good luck guys!
A school is building a new playground. They have spent 75% of the money for the new playground. If they have spent $1200, what is the total amount of money they will spend to build the playground? ASAP
Answers
Emily wants to buy a car. She has a choice between two different banks. One bank is offering a simple interest rate of 4.5% and the other bank is offering a rate of 4.5% compounded annually. Which is the better deal?
a simple interest rate of 4.5%
a compound interest rate of 4.5%
Answers
Answer: the simple interest rate of 4.5%
Step-by-step explanation:
What Is Simple Interest?
Simple interest is an interest charge that borrowers pay lenders for a loan. It is calculated using the principal only and does not include compounding interest. Simple interest relates not just to specific loans. It's also the type of interest that banks pay customers on their savings accounts.
The formula to determine simple interest is an easy one. Just multiply the loan's principal amount by the interest rate by the term.
This type of interest usually applies to automobile or short-term loans, although some mortgages use this calculation method.
What is compound interest?
Compound interest is the addition of interest to the principal sum of a loan or deposit, or in other words, interest on principal plus interest. It is the result of reinvesting interest, adding it to the loaned capital rather than paying it out, or requiring payment from the borrower so that interest in the next period is then earned on the principal sum plus previously accumulated interest. Compound interest is standard in finance and economics.
Compound interest is contrasted with simple interest, where previously accumulated interest is not added to the principal amount of the current period, so there is no compounding. The simple annual interest rate is the interest amount multiplied by the number of periods per year. The simple annual interest rate is also known as the nominal interest rate (not to be confused with the interest rate not adjusted for inflation, which goes by the same name).
What is the value of SS for the following set of scores?
Scores: 0, 1,4,5]
a. 18
b.42
c. Cannot answer without knowing whether it is a sample or a population
d. 7
Answers
The value of SS for the following set of scores [ 0, 1,4,5] is 42.
So, option b is correct
What is meant by sum of squares?The formula for measuring the deviation from the measured values is the Sum of Squares. The mean value of the complete collection of observed values is used to measure this distance.
When referring to a statistical method for calculating the dispersion of data points in regression analysis, the term "sum of squares" is employed. When determining which function best matches the data by deviating the least from it, the sum of squares can be utilized. Determine how well a data series can be fitted to a function that could aid in explaining how the data series was formed.
Given,
The dats is 0, 1, 4, 5
S0, the value of n is 4
SS=Sum of squares
SS=0²+1²+4²+5²
SS=0+1+16+25
SS=42
Therefore, the value of SS for the following set of scores [ 0, 1,4,5] is 42.
So, option b is correct.
To know more about sum of squares, visit:
https://brainly.com/question/29581249
#SPJ1
you have $15 and earn an additional $0.50 for each cup of water you sell. write an equation that represents the total amount of A (in dollars) you have after selling w cups of water
Answers
Answer: A = 15 + 0.5(w)
Step-by-step explanation: The above equation represents the amount of dollars after selling w cups of water. Remember: we also have 15 in advance, so we add that to the total amount of cups sold. We multiply 0.5 (the amount earned per water cup) by w (the number of water cups sold) and we will get our answer.
To check this, let's say we sold 10 water cups. So w = 10. Therefore, we write A = 15 + 0.5(10). That = A = 15 + 5 which A = 20. We can use any number in place of w now and we will know it is correct using this formula
What is the gradient of the surface?
Answers
The gradient of the surface can be described as a vector.
The gradient of a surface, which is a vector, represents the size and direction of the sharpest increase in value at a certain location. The magnitude of this vector, which denotes the direction of the greatest rate of rise of the surface, indicates how steep the rise is. The influence of this gradient is felt along a surface, which is the difference. It stands in for a unit that is level with the ground.
In mathematics, the vector grad f(x,y,z) = (df/dx, df/dy, df/dz) represents the gradient of a three-variable function with scalar values, f(x,y,z). Variables like optimization and electromagnetism employ the gradient of a surface, which is a crucial notion in vector calculus. In particular, the gradient of a surface is frequently used to compute the normal vector to a surface or to identify the direction of the steepest rise or drop in a landscape.
Read more about gradient of the surface on:
https://brainly.com/question/29638509
#SPJ4
to determine the confidence interval on the mean weight of filled buttercups, 40 samples are measured and found to have a mean value of 8 oz and a standard deviation of 0.2 oz. determine the confidence interval on the mean weight of buttercups with confidence levels of 90%, 95%, and 99%.
Answers
The confidence interval on the mean weight of buttercups with confidence levels of 90%, 95%, and 99% is (7.947981, 8.052019), (7.938019, 8.061981) and (7.918413, 8.081587).
The confidence level identifies the likelihood that an estimate of a statistical parameter's location in a sample survey is accurate for the entire population.
Confidence levels must be decided upon in advance when conducting a survey since they affect the survey's essential scope and error margin.
A determined statistical value based on a sample would have a 95% probability of being true for the entire population within the defined confidence level if the confidence level were set at 95%. In other words, there is a very strong likelihood that the population's arithmetic mean will fall inside the survey's defined margins of error.
For 90% confidence level:
Given a=0.1, |Z(0.05)|=1.645 (from standard normal table)
So 90% CI is
\(\bar x \pm Z\frac{s}{\sqrt{n} }\)
8 ± 1.645*0.2/√(40)
(7.947981, 8.052019)
For 95% confidence level:
Given a=0.05, |Z(0.025)|=1.96 (from standard normal table)
So 95% CI is
\(\bar x \pm Z\frac{s}{\sqrt{n} }\)
8 ± 1.96*0.2/√(40)
(7.938019, 8.061981)
For 99% confidence level:
Given a=0.01, |Z(0.005)|=2.58 (from standard normal table)
So 99% CI is
\(\bar x \pm Z\frac{s}{\sqrt{n} }\)
8 ± 2.58*0.2/√(40)
(7.918413, 8.081587).
Learn more about Confidence level:
https://brainly.com/question/17078485
#SPJ4
Evaluate a2 when a=3/4

Answers
Answer:
1/4
Step-by-step explanation:
answer key lang sakalam
#carry learning
What is the probability of rolling a sum of 5 on a standard pair of six-sided dice? express your answer as a fraction or a decimal number rounded to three decimal places, if necessary
Answers
The probability of rolling a sum of 5 on a standard pair of six sided dice is 1/9.
According to the given question.
A standard pair of dice is rolled.
So, the sample sapce for rolling a pair of dice = {(1,1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4),(5, 5),(5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
⇒ Total number of outcomes = 36
And, the outcomes for getting a sum of five on a sandard pair of six sided dice = {(2, 3), (3, 2), (4, 1), (1, 4)}
⇒ Total number of favorable outcomes = 4
As we know that " probability is the ratio of total number of favorable outcomes to the total number of outcomes".
Therefore,
The probability of rolling a sum of 5 on a standard pair of six-sided dice
= 4/36
= 1/9
Hence, the probability of rolling a sum of 5 on a standard pair of six sided dice is 1/9.
Find out more information about probability here:
https://brainly.com/question/11234923
#SPJ4
Which statement about the function fis false?
A) -2 and 1 are zeros of the function.
B) The function has a local minimum at x = 1 and a local maximum at x = -1.
C) The function is increasing when x < -1 and x > 1, and decreasing when -1 < x < 1.

Answers
The claim about the function that is false is At x = 1 and x = -1, respectively, the function has a local minimum and a local maximum.
what is function ?
The study of mathematics comprises the study of quantities and their variations, equations and associated structures, shapes and their positions, and locations where they can be found. A combination of inputs and corresponding outputs are referred to as a "function," which describes the relationship between them. The term "function" refers to an association between inputs and outputs where each input produces a single, unique result. There are two domains, or scopes, assigned to each function. Usually, the symbol f is used to signify functions (x). input is an x. There are four basic categories of functions that are available: on functions, one-to-one functions, many-to-one functions, within functions, and on functions.
given
Let y=x^x
⇒ dx/dy =x ^x (1+logx)
For increasing function, dx/dy >0
⇒x ^x (1+logx)>0
⇒1+logx>0
⇒log e
x>log e/e
⇒x> 1/e
Therefore, the function is increasing, when x> 1/e
The claim about the function that is false is At x = 1 and x = -1, respectively, the function has a local minimum and a local maximum.
To know more about function visit:
https://brainly.com/question/28193995
#SPJ1
what is the circumference if the diameter is 10/pi
Answers
Answer:
31.42cm
Step-by-step explanation:
We know that C = πd. Since the diameter is 10cm, we know that C = π x 10cm = 31.42cm (to 2 decimal places).
Answer:
31.42 centimeters.
Step-by-step explanation:
Are we in the same class? I had this same question and its due.
This season, the probability that the Yankees will win a game is 0. 61 and the probability that the Yankees will score 5 or more runs in a game is 0. 48. The probability that the Yankees lose and score fewer than 5 runs is 0. 32. What is the probability that the Yankees would score fewer than 5 runs when they lose the game? Round your answer to the nearest thousandth
Answers
Answer:
0.238
Step-by-step explanation:

a ski lift carried maria up a slope at the rate of 6 km/hr, and she skied back down parallel to the lift at 34 km/hr. the round trip took 30 minutes. how far did she ski and for how long?
Answers
Maria skied a distance of 2.55 km, taking 0.425 hours (25.5 minutes) going up and 0.075 hours (4.5 minutes) skiing down.
To find out how far Maria skied and for how long, we'll use the given information and apply the distance-rate-time formula. The formula is Distance = Rate × Time.
First, let's convert the given 30 minutes into hours since the rates are in km/hr.
30 minutes = 30/60 = 0.5 hours.
Let x be the distance Maria skied up and down, and let t1 and t2 be the time taken to go up and down, respectively.
For the ski lift(going up):
Distance = Rate × Time
x = 6 × t1
For skiing down:
Distance = Rate × Time
x = 34 × t2
Since the round trip took 0.5 hours, we have:
t1 + t2 = 0.5
Now we have a system of equations:
x = 6 × t1
x = 34 × t2
t1 + t2 = 0.5
From the first equation, we can express t1 as:
t1 = x/6
From the second equation, we can express t2 as:
t2 = x/34
Now substitute these expressions into the third equation:
(x/6) + (x/34) = 0.5
To solve for x, find a common denominator (in this case, 102) and combine the fractions:
(17x + 3x) / 102 = 0.5
20x = 51
x = 51/20
x = 2.55 km
Now, we can find t1 and t2:
t1 = x/6 = 2.55/6 = 0.425 hours
t2 = x/34 = 2.55/34 = 0.075 hours
So, Maria skied a distance of 2.55 km, taking 0.425 hours (25.5 minutes) going up and 0.075 hours (4.5 minutes) skiing down.
for more questions on distance
https://brainly.com/question/26046491
#SPJ11
Use linear approximation, i.e. the tangent line, to approximate as follows: Let f(x) = and find the equation of the tangent line to f(x) at a nice" point near 0.202. Then use this to 1/0.202 approximate 1/0.202

Answers
ANSWER
\(\begin{equation*} 4.95 \end{equation*}\)EXPLANATION
Given;
\(f\mleft(x\mright)=\frac{1}{x}\)Now, evaluate its first derivative;
\(f^{\prime}(x)=-\frac{1}{x^2}\)Now;
\(\begin{gathered} x=0.2=\frac{1}{5} \\ f(x)=5,f^{\prime}(x)=-25 \end{gathered}\)Hence, we have;
\(l(x)=5-25(x-0.2)=5-25x+5\)by substitution;
\(\begin{gathered} \frac{1}{0.202}=5.25(0.202-0.2) \\ =5-0.05 \\ \cong4.95 \end{gathered}\)4y + 3 ≤ 5 - 10y nhttjj
Answers
Answer:
heres ur answer
Step-by-step explanation:

Solve the initial value problem d y d x = 2 x 1 , y ( 0 ) = 2
Answers
Using separation of variables, it is found that the solution to the initial value problem is of y(x) = x² + 2.
What is separation of variables?In separation of variables, we place all the factors of y on one side of the equation with dy, all the factors of x on the other side with dx, and integrate both sides.
In this problem, the differential equation is given by:
\(\frac{dy}{dx} = 2x\)
Then, applying separation of variables:
\(dy = 2x dx\)
\(\int dy = \int 2x dx\)
\(y = x^2 + K\)
Since y(0) = 2, we have that the constant of integration is K = 2, and the solution is:
y(x) = x² + 2.
More can be learned about separation of variables at https://brainly.com/question/14318343
The differential equation is y(x) = x² + 2.
What is the differential equation?Differential Equations In Mathematics, a differential equation is an equation that contains one or more functions with their derivatives.
The given equation is;
\(\rm \dfrac{dy}{dx}=2x\)
Applying the variable separation method;
\(\rm \dfrac{dy}{dx}=2x\\\\\int\limits \, dy=\int\limits\, 2x. dx\\\\y = 2 \times \dfrac{x^{1+1}}{1+1} +c\\\\y = 2 \times \dfrac{x^{2}}{2} +c\\\\y = x^2+c\)
The value of c when y( 0 ) = 2 is c =2.
Hence, the required differential equation is y(x) = x² + 2.
More can be learned about the differential equation at;
brainly.com/question/14318343
#SPJ4
5a - 2b = 7 and 5a +2b =14 in elimination method
Answers
Answer:
a = 2.1
b = 1.75
Step-by-step explanation:
5a - 2b = 7
5a + 2b = 14
Combine the equation, we get
10a = 21
a = 2.1
Now put 2.1 in for a and solve for b
5(2.1) - 2b = 7
10.5 - 2b = 7
-2b = -3.5
b = 1.75
Let's Check
5(2.1) - 2(1.75) = 7
10.5 - 3.5 = 7
7 = 7
So, a = 2.1 and b = 1.75 is the correct answer.
5a + 2b = 14
———————- -
-4b = -7
b= 7/4
5 / 949 If they decide to drive 949 mi to Denver instead, how many miles will they drive each day?
Answers
If the question is asking how many miles will be driven each day over the course of 5 days in order to reach 949 miles, the answer is 949/5=189.8