a 1/2 gallon of milk costs 2.50.How much is milk per gallon?Figure that out any way you can.explain
Answers
Answer:
1 Gallon of milk = $5
Step-by-step explanation:
1/2 a gallon + 1/2 a gallon = 1 gallon
2.50 + 2.50 =$5
I hope i helped you :)
Related Questions
Hi! Can someone help me with these ?
A. 0.12
B. 1.2
C. 1.02
D. 1.3

Answers
Answer:
Hello!
The correct answer is B, or 1.2
Step-by-step explanation:
So first off we, have the number 1, two lines away from the dot, and there are 10 lines to the next number, which is 2, so it goes something like this:
1.
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.
so on and so forth, into infinity. But as for your problem, we can simply count the lines up to the dot, which puts us at 1.2
:^)
5Select the correct location on the imageClick the digt in the one thousands place814,593PresesAvert
Answers
Given the initial number 814,593, notice that it is equivalent to
\(814593=800000+10000+4000+500+90+3\)Therefore, the number 4 is in the one thousands place.
Barbara built a woodshed. She
made the base of the woodshed in
the shape of the drawing. What is
the area of the base of Barbara's
woodshed? Include the unit.
12 ft
6 ft
11 ft
7 ft
Answers
The area of the base of Barbara's woodshed is 72 square feet.
To find the area of the base of Barbara's woodshed, we need to know the shape of the base. In this case, the base is in the shape of a rectangle. A rectangle is a four-sided figure with opposite sides parallel and equal in length.
To calculate the area of a rectangle, we need to multiply its length by its width. In this case, the length of the rectangle is 12 feet, and its width is 6 feet. So, the area of the base of the woodshed is:
Area = Length x Width
Area = 12 ft x 6 ft
Area = 72 square feet
To know more about area here
https://brainly.com/question/14994710
#SPJ4
Complete Question:
Barbara built a woodshed. She made the base of the woodshed in the shape of the drawing. What is the area of the base of Barbara's woodshed? Include the unit. When the dimensions are given as 12 ft,6 ft, 11 ft and 7 ft.
CD is the perpendicular bisector of AB. AD = 6x-2 and DB = 2x + 18, Determine the value of x. A. x = [?] D C
Answers
Answer:
5
Step-by-step explanation:
The answer is 5
Put the following equation of a line into slope-intercept form, simplifying all fractions 2x + 6y = 36
Answers
Answer:
y=-\(\frac{1}{3} x+6\)
Step-by-step explanation:
Slope intercept form is y=mx+b. So, you solve for y by putting x to the other side and dividing by 6. In order it looks something like:
2x+6y=36
2x -2x +6y = 36 =2x
6y=36-2x
y=6-2/6x
y=6-1/3x
What is 5000 divided by 2000?
Answers
5000/2000=
5/2=
2 1/2=
2.5
Question Progress
Homework Progress
16/32 Marics
Toby goes on holiday to Geneva, Switzerland.
In Geneva, Toby sees a watch costing 193.75 CHF (Swiss Francs).
In Manchester, an identical watch costs £145.
Given that £1 = 1.55 CHF
a) In which city is the watch cheaper?
b) By how much is it cheaper (in £)?
Answers
So I was cheaper in Switzerland
how do i give brainliest? also please solve the problem :)

Answers
Answer:
When there are 2 answers there will be a crown you can click and that will give brainlest
Step-by-step explanation:
=
a + b + c
2
=
8 + 10 + 5
2
= 11.5 inches
Area = √s(s-a)(s-b)(s-c)
= √11.5×(11.5 - 8)×(11.5 - 10)×(11.5 - 5)
= 19.810035335658 inches
Answer:
the answer is 19.81 inches
the admission fee at an amusement park is 1.5 dollars for children and 4 dollars for adults. on a certain day, 351 people entered the park, and the admission fees collected totaled 1014 dollars. how many children and how many adults were admitted?
Answers
There were 682 children's and 332 adults were admitted when the entrance charge to an park is $4 for adults and $1.50 for children.
Given that,
The entrance charge to an amusement park is $4 for adults and $1.50 for children. 351 persons visited the park on one particular day, and 1014 dollars in entrance fees were collected.
We have to find how many people and kids were allowed inside.
We know that,
We get equations as,
1.5x+4y=351 ----->equation(1)
The other equation is
x+y=1014 ----->equation(2)
Take the equation(2)
x+y=1014
y=1014-x
Substitute y=1014-x in equation(1)
1.5x+4y=351
1.5x+4(1014-x)=351
1.5x+2056-4x=351
1.5x-4x=351-2056
-2.5x=-1705
2.5x=1705
x=1705/2.5
x=682
Substitute x=682 in equation(2)
y=1014-x
y=1014-682
y=332
Therefore, There were 682 children's and 332 adults were admitted when the entrance charge to an amusement park is $4 for adults and $1.50 for children.
To learn more about adults visit: https://brainly.com/question/28898057
#SPJ4
write a polynomial given the zeros of 0 (multiplicity 2), 1
Answers
Answer:
\(\displaystyle{P(x)=x^3-x^2}\)
Step-by-step explanation:
Given the zeros of 0, 0, 1. We can write the polynomial in form of x-intersects:
\(\displaystyle{P(x) = (x-x_1)(x-x_2)(x-x_3)}\)
Hence:
\(\displaystyle{P(x)=(x-0)(x-0)(x-1)}\)
Which can be simplified to:
\(\displaystyle{P(x)=x\cdot x \cdot (x-1)}\\\\\displaystyle{P(x)=x^2(x-1)}\)
Convert to the standard form by distributing x²:
\(\displaystyle{P(x)=x^2\cdot x - x^2 \cdot 1}\\\\\displaystyle{P(x)=x^3-x^2}\)
15-7=x+2 what is the missing number ?
Answers
The solution is : 42 is the missing number.
Here, we have,
given that,
2/35 = 1/30 +1/x
now, we have to find the missing number.
so, we have,
We want to know the missing denominator in the equation ...
2/35 = 1/30 +1/x
Solution
Subtract 1/30 from both sides and simplify.
2/35 -1/30 = 1/x
(2·30 -1·35)/(35·30) = 1/x
25/(35·30) = 1/x
1/(7·6) = 1/42 = 1/x
The missing denominator is 42.
Hence, The solution is : 42 is the missing number.
To learn more on multiplication click:
brainly.com/question/5992872
#SPJ1
complete question:
What is the missing number?
2/35 = 1/30 +1/x
A bored college student on top of a 6-story tall building drops a water balloon on his friends directly below. In one second it falls one story down from the top. In one more second it will be:
Answers
Therefore, the water balloon will be on the fourth story in one more second.
The acceleration due to gravity is approximately 9.8 m/s^2. Since the water balloon falls one story down (which is approximately 6 meters) in one second, we can calculate its initial velocity using the equation: d = 1/2at^2. Plugging in the values, we get: 6 = 1/2(9.8)t^2, which simplifies to t = sqrt(1.2245) ≈ 1.11 seconds. Therefore, in one more second, the water balloon will have fallen another story down, i.e., it will be on the fourth story.
The water balloon dropped by the bored college student falls one story down from the top in one second. To calculate how long it will take for it to fall another story down, we can use the equation: d = 1/2at^2, where d is the distance, a is the acceleration due to gravity, and t is time. Plugging in the values, we get t = sqrt(1.2245) ≈ 1.11 seconds.
Therefore, the water balloon will be on the fourth story in one more second.
To know more about equations visit:
https://brainly.com/question/22688504
#SPJ11
Find n in this equation
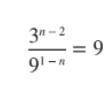
Answers
The value of the variable n in the given equation, (3ⁿ⁻²) / (9¹⁻ⁿ) = 9, is 2
Solving the equation for variable nFrom the question, we are to solve the given equation for the given variable n.
The given equation is
(3ⁿ⁻²) / (9¹⁻ⁿ) = 9
To solve the equation, we will determine the value of n
First multiply both sides of the equation by (9¹⁻ⁿ)
(9¹⁻ⁿ) × (3ⁿ⁻²) / (9¹⁻ⁿ) = 9 × (9¹⁻ⁿ)
(3ⁿ⁻²) = 9 × (9¹⁻ⁿ)
3ⁿ⁻² = 9 × 9¹⁻ⁿ
Applying the multiplication law of indices
3ⁿ⁻² = 9¹⁺¹⁻ⁿ
3ⁿ⁻² = 9²⁻ⁿ
Express 9 as an exponent
3ⁿ⁻² = 3²⁽²⁻ⁿ⁾
since the bases are equal, equate the exponents
n - 2 = 2(2 - n)
Distribute 2 on the right side of the equation
n - 2 = 4 - 2n
n + 2n = 4 + 2
3n = 6
Divide both sides by 3
3n/3 = 6/3
n = 2
Hence, the value of n is 2
Learn more on Solving equation here: https://brainly.com/question/27882730
#SPJ1
a hat company charges a design fee plus $4 per hat. the total cost of 5 hats is $30. how much will it cost for 3 hats?
Answers
Using Algebraic expression solution ,
The cost of three hats is $18 .
We have given that,
A hat company charge for design fee $4 per hat .
i.e design fee of one hat = $4
total cost of 5 hats = $30
let the cost of one hat without design fee be $x and total cost of one hat is $(x+4) .
using the above statement, we get an algebraic expression,
5( x+ 4)= 30
we solve the above algebra expression,
=> 5x + 20 = 30
=> 5x = 10
=> x = 2
so, cost of a hat without design fee is $2
and total cost of one hat is $6.
we have to calculate cost of 3 hats .
cost of one hat in hat company= $ 6
cost of three hats in hat company= $(6×3)
= $18
Hence, the total cost of 3 hats is $18.
To learn more about Algebraic expression , refer:
https://brainly.com/question/22763064
#SPJ4
a student has a class that is supposed to end at 9:00am and another that is supposed to begin at 9:15am. suppose the actual ending time of the 9am class is normally distributed random variable (x1) with a mean of 9:02 and a standard deviation of 2.5 minutes and that the starting time of the next class is also a normally distributed random variable (x2) with a mean of 9:15 and a standard deviation of 3 minutes. suppose also that the time necessary to get from one class to another is also a normally distributed random variable (x3) with a mean of 10 minutes and a standard deviation of 2.5 minutes. what is the probability that the student makes it to the second class before the second lecture starts? (hint: assume x1, x2 and x3 are independent also think linear combinations)
Answers
The probability that the student makes it to the second class before it starts is very close to 0.
To find the probability that the student makes it to the second class before it starts, we can use the concept of linear combinations of random variables and the properties of normal distributions.
Let's define the random variable X as the total time it takes for the student to transition from the end of the first class to the start of the second class. Since X is a linear combination of independent normally distributed random variables (X1, X2, X3), we can use their means and variances to calculate the mean and variance of X.
The mean of X is the sum of the means of X1, X2, and X3:
μX = μ1 + μ2 + μ3 = 9:02 + 9:15 + 10 = 28:17 minutes.
The variance of X is the sum of the variances of X1, X2, and X3:
σX^2 = σ1^2 + σ2^2 + σ3^2 = (2.5)^2 + (3)^2 + (2.5)^2 = 15.25 minutes^2.
Now, we need to calculate the probability that X is less than or equal to 0, meaning the student arrives before the second lecture starts. Since X follows a normal distribution, we can standardize the variable and calculate the probability using the standard normal distribution table.
Z = (0 - μX) / σX = (0 - 28:17) / √15.25 ≈ -9.43.
Using the standard normal distribution table or a calculator, we can find the probability corresponding to Z = -9.43. The probability is essentially 0, as the value is significantly far in the left tail of the standard normal distribution.
Therefore, the probability that the student makes it to the second class before it starts is very close to 0.
To learn more about probabilty click here:
brainly.com/question/21133306
#SPJ11
The factorization of x2 3x – 4 is modeled with algebra tiles. An algebra tile configuration. 2 tiles are in the Factor 1 spot: 1 is labeled x, 1 is labeled negative. 5 tiles are in the Factor 2 spot: 1 is labeled x and 4 are labeled. 10 tiles are in the Product spot: 1 is labeled x squared, 1 is labeled negative x, the 4 tiles below x squared are labeled x, and the 4 tiles below the negative x tiles are labeled negative. What are the factors of x2 3x – 4? (x 4) and (x – 4) (x 3) and (x – 4) (x 4) and (x – 1) (x 3) and (x – 1).
Answers
The factors of the equation are 4 and -1.
Given
Equation; \(\rm x^2+3x-4\)
What is a quadratic equation?The polynomial which has the highest degree is 2 is called the quadratic equation.
The standard form of the quadratic equation is;
\(\rm ax^2+bx+c=0\)
The factors of the given equation are;
\(\rm x^2+3x-4=0\\\\x^2-4x+x-4=0\\\\x(x-4)+1(x-4)=0\\\\ (x-4)(x+1)=0\\\\x-4=0, \ \ x=4\\\\x+1=0, \ \ x=-1\)
Hence, the factors of the equation are 4 and -1.
To know more about Factors click the link given below.
https://brainly.com/question/16975319
Answer:
c
Step-by-step explanation:
The flight path of a rocket, launched from the ground, is modeled by y = 0.5(20x – x2), where y is the height of the rocket in feet from the ground and x is the time in seconds after it was launched. Find the vertex of the parabola and explain what it represents in terms of the context.
a. (20, 0); rocket lands at 0 feet after 20 seconds
b. (10, 50); rocket reaches maximum height of 50 feet after 10 seconds
c. (10, 50); rocket reaches maximum height of 10 feet after 50 seconds
d. (20, 0); rocket reaches 20 feet after 0 seconds
Answers
Answer: B. (10, 50)
Step-by-step explanation:
y = 0.5(20x - \(x^{2}\))
\(y=-\frac{1}{2} x^{2} + 10x\)
to find x coord of vertex use the equation
\(\frac{-b}{2a}\)
\(x=\frac{-10}{-1} \\\\x=10\)
plug in x to the original equation
y = 0.5(20(10) - \((10)^{2}\)
y = 0.5(100)
y = 50
Answer: (10, 50)
Please help if you can

Answers
The exponential function that satisfies the given conditions is given as follows:
\(f(t) = 4e^{1.099t}\)
How to model the exponential function?The format of the exponential function for this problem is given as follows:
f(t) = 4e^(kt).
In which k is the exponential growth rate.
After five hours, there was 972 bacteria, meaning that when t = 5, f(t) = 972, hence the growth rate is obtained as follows:
\(972 = 4e^{5k}\)
\(e^{5k} = 243\)
5k = ln(243)
k = ln(243)/5
k = 1.099.
Meaning that the function is defined as follows:
\(f(t) = 4e^{1.099t}\)
More can be learned about exponential functions at https://brainly.com/question/25537936
#SPJ1
I dont know how to do this
pls answer if u know with simple working
i dont know if u add 4 each time it didnt work for last questionn

Answers
I don't know how to solve this 2/4 + 3/8=?
Answers
Answer:
7/8
Step-by-step explanation:
look it up
your wel3
Answer: \(\frac{7}{8}\) or 0.875 in decimal form.
Step-by-step explanation:
Okay, so to solve this, the easiest method is to find a common denominator. While we could try using trial and error or if you know your tables really well, I don't so we will just multiply the denominators which is 8 and 4. We then multiply 8 and 4 which is 32.
To convert the fractions we have, we multiply both the numerator and denominator of each, by the multiple that multiplies the denominator to 32.
\(\frac{2}{4}\) multiply both 4 and 2 by 8. Now we have \(\frac{16}{32}\).
Same thing with the second number. We have \(\frac{3}{8}\). We multiply both the numerator and the denominator by 4. 3*4 is 12, 8*4 is 32.
Now we have \(\frac{12}{32}\).
Now that both fractions have common denominators, we can add the numerators. \(\frac{16}{32} +\frac{12}{32} = \frac{28}{32}\)
Now we have the answer, \(\frac{28}{32}\), but is that it?
No. Now to find the final two answers, we simply \(\frac{28}{32}\).
To simplify, we find the Greatest Common Factor of 28 and 32, which in this case happens to be 4. This is the highest number that either of those can be divided by to provide a normal whole number
After solving \(\frac{28/4}{32/4} =\frac{7}{8}\)
That is our final answer. \(\frac{7}{8}\).
If necessary, you can convert it to decimal form through simple division and end up with 0.875.
g the size of bass caught in strawberry lake is normally distributed with a mean of 11 inches and a standard deviation of 3 inches. suppose you catch 4 fish. what is the probability the average size of the fish you caught is more than 13 inches?
Answers
The probability that the average size of the fish you caught is more than 13 inches is approximately 0.0918, or about 9.18%.
We can use the Central Limit Theorem to approximate the distribution of the sample mean. According to the theorem, the sample mean of a sufficiently large sample will be approximately normally distributed with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
In this case, we have a sample size of 4, which may not be considered sufficiently large, but we can still use the approximation. Thus, the distribution of the sample mean can be approximated as:
mean = 11
standard deviation = 3 / sqrt(4) = 1.5
To find the probability that the average size of the fish you caught is more than 13 inches, we need to standardize the sample mean using the z-score formula:
z = (x - mean) / standard deviation
where x is the sample mean we want to find the probability for. Plugging in the values, we get:
z = (13 - 11) / 1.5 = 1.33
Now, we need to find the probability of getting a z-score greater than 1.33 in a standard normal distribution table or calculator. Using a calculator or statistical software, we find that this probability is approximately 0.0918.
Therefore, the probability that the average size of the fish you caught is more than 13 inches is approximately 0.0918, or about 9.18%.
Learn more about probability at
brainly.com/question/31120123
#SPJ4
Please help and show how you did it!!

Answers
Answer
EAD= EBC true.
Step-by-step explanation:
Both triangles are equal. The line between AE and EB show the lines are equal. In turn this makes the sides AD and BC equal. DC are the same length as AE and EB. In short, all sides are equal so the triangles are the same.
write a linear equation in the form of y=mx+b

Answers
Answer:
y=6x-4
(dark blue)
Step-by-step explanation:
x=0 y=-4
y=6x-4
y=6(0)-4
y=-4
What is an equation of the line that contains the point (0, -5) and a slope of 1/4
Answers
Answer:
y=1/4x-5
Step-by-step explanation:
Answer:
y = 1/4x - 5
Step-by-step explanation:
y = mx + b is the equation of a straight line.
m = slope, b = y intercept. (y intercept is the point where the line of the graph crosses the y axis)
(0, -5) is the y intercept (if you were to graph this point, it would be on the y axis, fitting the previous description)
the slope is 1/4
replace each variable in the equation, and you get:
y = 1/4x - 5
Line c has an equation of y= 4 3 x+9. Line d is parallel to line c and passes through ( – 4, – 4). What is the equation of line d?
Answers
The answer to your question is y = -1/2x + 2
We have given that,
Line c has an equation of y= 4 3 x+9. Line d is parallel to line c and passes through ( – 4, – 4)
Data, Line C y = -1/2x - 2
Line D =?
Point = (8, -2) Process
1.- Get the slope of line C. The slope is the coefficient of the letter x.
y = -1/2x - 2
slope = -1/2
2.- Get the slope of line D. As the lines are parallels, the slope is the same.
slope = -1/2
3.- Find the equation of line D
What is the slope point form?y - y1 = m(x - x1)
We use the substitution method
y + 2 = -1/2(x - 8)
We simplify the given equation
y + 2 = -1/2x - 8(-1/2)
y + 2 = -1/2x + 4
y = -1/2x + 4 - 2
The equation of line d is y = -1/2x + 2.
To learn more about the equation visit:
https://brainly.com/question/2972832
#SPJ1
Can someone please help me with this problem?

Answers
Answer: 18/9 if not it's something along that-
Step-by-step explanation:
7^2 = 49 so like 49-31 equals 18 and the denominator 3^2 = 9 , so if it's not 18/9 then it's like 1/2 or something bc 9 + 9 is 18 yk-
what solution does this system have? y=3x+2 and y=3x-6

Answers
If the Two Lines are parallel, then the pair has no solution and is called inconsistent. This system has No Solution.
What is inconsistent?If the Two Lines are parallel, then the pair has no solution and is called inconsistent.
Given: y=3x+2
y=3x-6
Standard equation of line is: ax+by+c=0
Here ,Two standard equations of line are: a₁x + b₁y + c₁ =0
a₂x + b₂y + c₂=0
Compare these equation to the given equations to find out the value of a₁ ,b₁ ,c₁, a₂, b₂ ad c₂.
a₁=3 b₁=-1 c₁=2 and a₂=3 b₂= -1 c₂= -6
\(\frac{a_1}{a_2} =\frac{b_1}{b_2} \neq \frac{c_1}{c_2} \\\frac{3}{3}= \frac{-1}{-1}\neq \frac{2}{-6}\) ( after putting the value)
If the Two Lines are parallel, then the pair has no solution and is called inconsistent. This system has No Solution.
To Know more about inconsistent, Visit: https://brainly.com/question/28586540
#SPJ1
you drop a ball off a 50 foot roof to see how long it will bounce. Each bounce loses 10% of the height of its previous bounce. after how many bounces will the ball's height be less than 1 foot?
Answers
After 37 bounces, the ball's height will be less than 1 foot.
How many bounces until it is less than 1 foot?The initial height of the ball is 50 feet.
After first bounce, the ball will reach a height of:
= 50 feet * (1 - 10%)
= 45 feet.
After second bounce, it will reach a height of:
= 45 feet * (1 - 10%)
= 40.5 feet.
Height decreases by 10% after each bounce.
We have to set up an equation:
50 feet * (0.9)^n < 1 foot
Simplifying:
0.9^n < 1/50
Taking the logarithm:
n * log(0.9) < log(1/50)
n > log(1/50) / log(0.9)
n > 37.1298771746
n > 37.13.
Read more about height
brainly.com/question/1739912
#SPJ1
Two people are standing on opposite sides of a small river. One person is located at point Q, a distance of 25 meters
from a bridge. The other person is standing on the southeast corner of the bridge at point P. The angle between the
bridge and the line of sight from P to Q is 73. 8°. Use this information to determine the length of the bridge and the
distance between the two people.
Answers
Length of Bridge = 7.26 metres
Distance between the 2 people = 26.04 metres
The figure is attached below, to give you a clearer idea of the situation of the bridge and the 2 people.
Distance between Q and the bridge = 25m
Angle = 73.8°
Since P is located on the bridge (south-east corner), we can find the length of the bridge using tan 73.8°.
tan θ = height/base
tan 73.8° = 25/length of bridge
Let length of bridge =x.
⇒ 3.442 = 25/x
⇒ x = 25/3.442 = 7.2632 ≅ 7.26 metres.
To find the distance between P and Q (the 2 people), we can use sin 73.8°.
sin θ = height/hypotenuse
sin 73.8° = 25/distance between P and Q
Let distance between P and Q = y
sin 73.8° = 25/y
⇒ 0.96 = 25/y
⇒ y = 25/0.96 = 26.04166 ≅ 26.04 metres
Therefore, the distance between the 2 people = 26.04 metres, and the length of the bridge over the river = 7.26 metres.
To learn more about trigonometry, visit the link:
brainly.com/question/13971311
#SPJ4

Does anyone know this

Answers
Answer:
2.5
Step-by-step explanation:
2.5
Answer:
2.5s
Step-by-step explanation:
Time = \(\frac{Distance}{Speed} =\frac{5 meters}{2m/s} =2.5s\)