A farm lets you pick 2 pounds of blueberries for 5 dollars.
1. the unit rate of dollars to pounds is ___ dollars per 1 pound
2. the unit rate of pounds to dollars is ___ pounds per 1 dollar
Answers
Answer:
1. $2.50
2. 2/5lb
Step-by-step explanation:
1. 2lbs=$5.00 so that means 1lb=$2.50.
2. 1lb=$2.50 so that means 1/5lb=$0.50 which you can then conclude that 2/5lb=$1.00
Related Questions
Simplify the expression. 54−6 ⋅ 5÷3 Enter your answers in the boxes. 54−6 ⋅ 5÷3 =54− ÷3 =54− =
Answers
Here it is, can u give me a brainliest answer???

I don’t understand this type of question
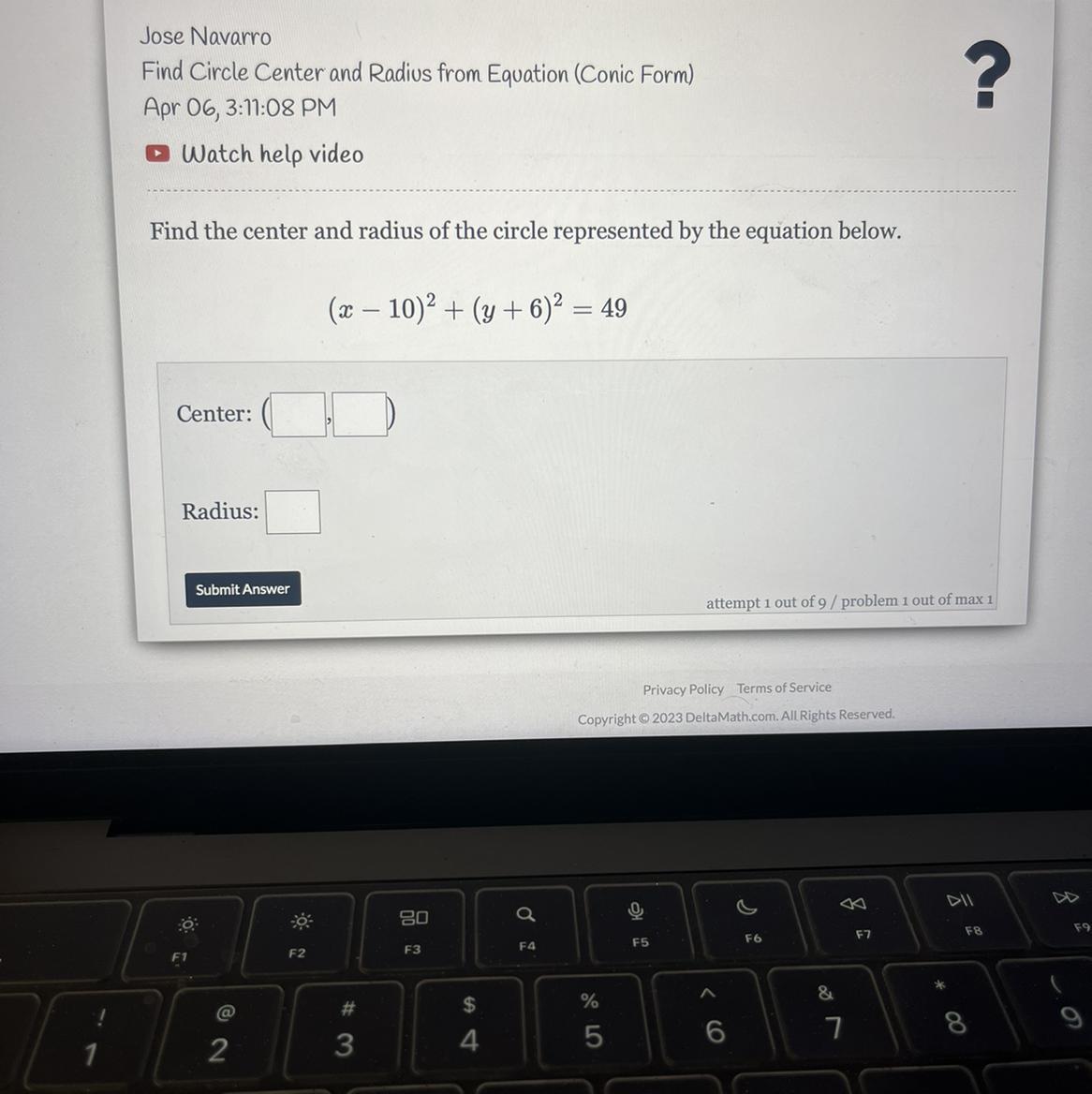
Answers
Answer:
Center: 10, -6, Radius: 7
Step-by-step explanation:
This equation can be rewritten using the formula
(x-p)²+(y-q)²=r²
From this we get that p=10 and q=-6, because -(-6)=+6. This is how we get the center points.
And since the square root of 49 is 7, we see that the radius is 7.
What is the scale factor of the dilation?

Answers
Answer:
2
Step-by-step explanation:
Scale factor tells how much the size of the figure increases or decreases. Part A shows that the larger figure is twice the size of the smaller figure. So, the scale factor of this dilation is 2.
Question, Please HELP AND EXPLAIN if anyone knows the answer and the explanation. I don't get it how you solve it.
Hannah, who lives in Charleston, SC, is taking a road trip with her father all the way across the country to Los Angeles, CA. She wants to draw an accurate map of the United States to document the journey. If she is drawing the country on a standard piece of paper (81/2 inches by 11 inches) and the USA is -2,500 miles wide, what is the most appropriate unit selection for the legend of the map?
Options.
1 in. to 20 miles
1/2 in. to 125 miles
1/4 in. to 400 miles
Why did you choose that answer? Use at least 2 complete sentences. What is another option for units that would be appropriate for this situation? Use at least 2 complete sentences to defend your response.
Answers
Using proportions, the most appropriate unit selection for the legend of the map 1/2 inches to 125 miles.
This scale was chosen applying the proportion between the width of the United States and the width of the piece of paper, and another possible scale is of 1 inch to 20 miles.
What is a proportion, and why are they used for scale problems?A proportion is a fraction of a total amount, and equations can be built to find the desired measures in the problem using a rule of three, that can be either direct(cross multiplication) or inverse(line multiplication), deriving from proportional relationships.
One example of application of proportions is for scale problems, in which we find the scales are applied to find the real distances, or vice-versa.
For this problem, the country is drawn on a paper with these following dimensions:
81/2 = 41.5 inches to 11 inches.
Since the United States is 2,500 miles wide, we have that:
2500/41.5 = 60 (approximately).
Hence the scale could be of:
1 inch - 60 miles.
Applying half to the proportion, and approximating, an scale is:
1/2 inches to 125 miles.
Which is the appropriate unit selection.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
why do i have so many grey hairs and i’m only 16
Answers
Answer:
it could possibly be because of stress. Do you stress alot?
Step-by-step explanation:
On a coordinate plane, a triangle is located at (3, 4), and a square is located at
(10, 4). What is the distance between the square and triangle?
Answers
Answer:
7
Step-by-step explanation:
Answer:
7 units north
Step-by-step explanation:
Count from 3,4 to 10,4 and there are seven units
The value of the series 4+9+14+dots +(5n-1) by using the summation notation equals
Answers
The value of the series 4 + 9 + 14 + ... + (5n-1) using the summation notation is (5n^2 + 3n)/2.
The value of the series 4 + 9 + 14 + ... + (5n-1) can be found using the summation notation as follows:
Identify the first term, common difference, and number of terms in the series. The first term is 4, the common difference is 5, and the number of terms is n.
Use the summation notation to write the series as ∑_{i=1}^{n} (5i-1).
Use the formula for the sum of an arithmetic series to find the value of the series. The formula is S_n = n/2 (a_1 + a_n), where S_n is the sum of the series, n is the number of terms, a_1 is the first term, and a_n is the last term.
Substitute the values of n, a_1, and a_n into the formula and simplify. S_n = n/2 (4 + (5n-1)) = n/2 (5n+3) = (5n^2 + 3n)/2.
The value of the series is (5n^2 + 3n)/2.
Therefore, the value of the series 4 + 9 + 14 + ... + (5n-1) using the summation notation is (5n^2 + 3n)/2.
Learn more about Notation
brainly.com/question/29531272
#SPJ11
how many 3-letter strings can we make from the letters a, b, c, and d, if we are allowed to repeat letters, and we must use the letter a at least once?
Answers
We can make 37 , 3-letter strings from the letters a, b, c, and d.
How many 3-letter strings can we make?1 . AAA - This word could be written in 1 way.
2. AAB, AAC, AAD
Each word could be written in 3 ways 3*3=9 ways3.ABB, ACC, ADD
Each word could be written in 3 ways 3*3=9 ways4. ABC, ABD, ACD
Each word could be written in 6 ways as they are unique and does not have repetitive letters.3*6 = 18 waysTotal = 1+9+9+18
= 37
So, we can make 37 3-letter strings from the letters a, b, c, and d by applying the method called permutation.
What is permutation?When the order of the arrangements matters, a mathematical technique called a permutation can be used to calculate the number of alternative arrangements in a collection. Only a few elements from a collection of options must be selected in a specific order in order to solve common mathematical problems. Combinations, a different mathematical concept, are frequently mistaken with permutations. The combination, however, does not depend on the order of the selected components. In other words, the arrangements ab and be in permutations are regarded as different arrangements, whereas they are equal in combinations.It is a term that refers to the various possible arrangements or orders of things. The arrangement's order matters in permutations.To learn more about permutation, refer:
https://brainly.com/question/1216161
#SPJ1
Find (if possible) the rational zeros of the function. (Enter your answers as a comma-separated list. If an answer does not exist, enter DNE.)
C(x) = 2x3 + 3x2 − 1
Answers
Therefore, the possible rational zeros of C(x) are -1/2, 1/2, -1, 1, -2, and 2.
To find the rational zeros of the function C(x), we need to find the factors of the constant term -1 and the factors of the leading coefficient 2. Then we can form all possible fractions that can be obtained by dividing the factors of the constant term by the factors of the leading coefficient.
The factors of -1 are ±1 and ±1/2, and the factors of 2 are ±1 and ±2. Therefore, the possible rational zeros of C(x) are:
±1/2, ±1, ±1/2, ±1/1, ±2/2
Simplifying these fractions, we get:
±1/2, ±1, ±2
To know more about possible rational zeros,
https://brainly.com/question/31054413
#SPJ11
The fee that a driver pays to have automobile insurance is called a deductible
o
A. True
B. False
Answers
A box contains 14 large marbles and 10 small marbles. Each marble is either green or white 8 of the large marbles are green, and 4 of the small
marbles are white. If a marble is randomly selected from the box, what is the probability that it is large or white? Express your answer as a fraction
or a decimal number rounded to four decimal places.
Pls step by step :)) thank you!
Answers
The probability that the marble is large or white is 0.5714.
What is probability?
Probability is the branch of mathematics that studies the possible outcomes of given events together with the outcomes' relative likelihoods and distributions.
Probability of an event is
P(A) = Number of favorable outcomes/ Total Number of outcomes
= n(A)/n(S)
where
P(A) is the probability of an event “A”
n(A) is the number of favorable outcomes
n(S) is the total number of events in the sample space.
We have,
Number of large marbles = 14
Number of small marbles = 10
Number of large green marbles = 8 which implies
Number of large white marbles = 14 - 8 = 6
Number of small white marbles = 4 which implies
Number of small green marbles = 10 - 4 = 6.
Now, let
Let X be the event of drawing large marble.
Let Y be the event of drawing small marble.
Let M be the event of drawing white marbles.
Let N be the event of drawing green marbles.
Since only one marble is drawn at a time ,
so P(X) = 14/24
P(Y) = 10/24
P(M) = 10/24
P(N) = 14/24
We have to find the probability that a marble is large or white i.e. P(X∪M).
P(X∪M) = P(X) + P(Y) - P(X∩M)
P(X∩M) = In 14 large marbles 6 are white marbles = 6/14.
P(X∪M) = P(X) + P(Y) - P(X∩M) = 14/24 + 10/24 - 6/14 = 0.5833+0.4167-0.4286 = 0.5714.
Therefore, the probability of drawing large or white marble is 0.5714.
To know more about probability, visit
https://brainly.com/question/19169117
#SPJ4
Write each as an algebraic expression

Answers
Answer:
4^3
11>6
y>2
13-x
Step-by-step explanation:
4 is to the third power
11 is greater than 6 which means u use this sign >
y is greater than 2
13 subtract x
How can ure out the next number in the pattern below? Write a conjecture that describes the pattern.
29, 28, 26, 23, 19
Answers
The difference between consecutive first and second integers is increased by 1 thus the next number 19 - x = 5 → x = 14.
What is the pattern?A pattern is a specific arrangement of numbers or any term which will follow a specific code or hint.
For example 2,4,6,8 in this, the difference between any two-term is only 2 and this will be its specific pattern.
As per the given pattern,29, 28, 26, 23, 19
29 - 28 = 1
28 - 26 = 2
26 - 23 = 3
23 - 19 = 4
Since the difference is increasing by 1
So the difference of 19 and the next number (x) will be 4 + 1 = 5.
19 - x = 5
x = 14
Hence "The difference between consecutive first and second integers is increased by 1 thus the next number 19 - x = 5 → x = 14".
For more information about the pattern,
brainly.com/question/14013716
#SPJ2
A sphere is inscribed in a cube, and the cube has a surface area of 24 square meters. A second cube is then inscribed within the sphere. What is the surface area in square meters of the inner cube
Answers
Check the picture below, I'll be referring to the material in the picture.
we know the outer cube has a surface area of 24, we also know is a cube, so it has 6 equal sides which are squares each, let's say the side of one of those squares in the cube is say of length "s", so the area of one square will just be s², and for 6 squares that'll be an area of 6s², that is the area of the outer cube, which we know is 24.
\(24=6s^2\implies \cfrac{24}{6}=s\implies 4=s^2\implies \sqrt{4}=s\implies 2=s\)
now, we know the sphere is inscribed in the outer cube, so it's touching its edges, like you see in the picture in blue, so if we get a cross-section of the whole lot, we'd get the picture to the right of blue cube in the picture, an outer cube with a side of 2, and therefore an sphere with a diameter of 2, and thus a radius of 1, as you can see in the red triangle.
Let's notice that the red triangle is a 45-45-90 triangle, and thus we can use the 45-45-90 rule to get its sides, as you can see in the picture on the far-right, which gives us half of one side of the inner cube to be 1/√2.
\(\stackrel{\textit{half a side}}{\cfrac{1}{\sqrt{2}}}\qquad \stackrel{\textit{a full side}}{\cfrac{1}{\sqrt{2}}+\cfrac{1}{\sqrt{2}}}\implies \cfrac{2}{\sqrt{2}}\implies \cfrac{2\sqrt{2}}{\sqrt{2}\sqrt{2}}\implies \cfrac{2\sqrt{2}}{2}\implies \sqrt{2}\)
now as you can see in the picture, the inner cube in orange, has 6 sides, each side is √2 long, so let's get the 6 squares area.
\(\stackrel{\textit{area of one square}}{\sqrt{2}\cdot \sqrt{2}\implies 2}\qquad \stackrel{\textit{area of all 6 sides of the inner cube}}{6\cdot 2\implies 12}\)

Pls explain your answer. Thanks in advance. I will mark brainliest if u explain

Answers
Step-by-step explanation:
Using Trigonometry,
tan33° = Opposite/Adjacent = GF/DF.
Therefore GF = DF * tan33°
= 235tan33° = 152.6.
Angle GEF = Angle EDG + Angle DGE
= 33° + 34° = 67°. (Exterior Angle Theorem)
Using Trigonometry,
sin67° = Opposite/Hypotenuse = GF/EF.
Therefore EF = GF / sin67°
= 152.6 / sin67° = 165.8.
Hence the answer is the 1st option.
Answer:
the answer is A. GF =152.6 and EG=165.8
GF= 235*(tan(33))
EG= 152.6/(sin(67))
please answer from the attachment

Answers
Look at the attached picture
Hope it will help you..
Good luck for the test...
(◕ᴗ◕✿)(ʘᴗʘ✿)

An electronic chess game has a useful life that is exponential with a mean of 30 months. The length of service time after which the percentage of failed units will approximately equal 50 percent? 9 months 16 months 21 months 25 months QUESTION 17 A majof television manufacturer has determined that its 50 -inch LED televisions have a mean service life that can be modeled by a normal distribution with a mean of six years and a standard deviation of one-haif year. What probability can you assign to service lives of at least five years? (Please keep 4 digits after the decimal point
Answers
In the case of the electronic chess game, with a useful life that follows an exponential distribution with a mean of 30 months, we need to determine the length of service time after which the percentage of failed units will approximately equal 50 percent. The options provided are 9 months, 16 months, 21 months, and 25 months.
For the major television manufacturer, the service life of its 50-inch LED televisions follows a normal distribution with a mean of six years and a standard deviation of half a year. We are asked to calculate the probability of service lives of at least five years.
1. Electronic Chess Game:
The exponential distribution is characterized by a constant hazard rate, which implies that the percentage of failed units follows an exponential decay. The mean of 30 months indicates that after 30 months, approximately 63.2% of the units will have failed. To find the length of service time when the percentage of failed units reaches 50%, we can use the formula P(X > x) = e^(-λx), where λ is the failure rate. Setting this probability to 50%, we solve for x: e^(-λx) = 0.5. Since the mean (30 months) is equal to 1/λ, we can substitute it into the equation: e^(-x/30) = 0.5. Solving for x, we find x ≈ 21 months. Therefore, the length of service time after which the percentage of failed units will approximately equal 50 percent is 21 months.
2. LED Televisions:
The service life of 50-inch LED televisions follows a normal distribution with a mean of six years and a standard deviation of half a year. To find the probability of service lives of at least five years, we need to calculate the area under the normal curve to the right of five years (60 months). We can standardize the value using the formula z = (x - μ) / σ, where x is the desired value, μ is the mean, and σ is the standard deviation. Substituting the values, we have z = (60 - 72) / 0.5 = -24. Plugging this value into a standard normal distribution table or using a calculator, we find that the probability of a service life of at least five years is approximately 1.0000 (or 100% with four digits after the decimal point).
Therefore, the probability of service lives of at least five years for 50-inch LED televisions is 1.0000 (or 100%).
Learn more about exponential distribution here: https://brainly.com/question/28256132
#SPJ11
I’m having trouble on this problem, anyone know the answer?

Answers
Answer:
the answer is 35 cm
Step-by-step explanation:
to make sure that you dont have a problem next time here is a formula
area of any polygon is the sum of all sides so 9 + 9 + 12 + 5 = 35
To find the area of ABCDE, the two equations you will need are:
Rectangle = l • w
Triangle = (b • h)/2
Since rectangles are symmetrical, we can ignore the triangle for now.
Observe that the left side of the rectangle states 5 cm, and the bottom side states 12 cm. With this information we can infer that:
Area of rectangle is 12cm(5cm) = 60cm^2
Alright, now we can look at the triangle. What we’ll do is subtract 5cm from 9cm to get the height 4 cm; and we’ll subtract 9 cm from 12 cm to get the base 3 cm.
With this information, we can conclude that the area of the triangle (3cm(4cm)/2 = 6cm^2
Adding both the triangle and rectangle area together, we get 66cm^2
hope you you are succes in this question ❓❓

Answers
Answer:
Yes bro I can sove this question
Step-by-step explanation:
Please mark me brainliest thanks
A box of cereal has a width of 4 inches, and a length of 8 inches and a height of 12 inches. What is the volume of the box, in cubic inches?
Use the formula V = wh where V represents the volume, / represents the length, w represents the width, and h represents the height.
4 in.
12 in.
8 in
Answers
Answer:
384
Step-by-step explanation:
multiply all those numbers together
The function y=-16x^2+10,000 represents the elevation y (in feet) of a skydiver x seconds after jumping from an airplane until deploying a parachute at an elevation of 3600 feet. How long after jumping from the airplane does the skydiver deploy the parachute?
Answers
The skydiver deploys the parachute 20 seconds after jumping from the airplane.
Describe Elevation.The elevation is a term used to describe the vertical distance above or below a reference point or surface, usually the Earth's surface. In the context of a plane, elevation refers to the height of the plane above or below the ground or sea level.
The elevation is typically measured in feet or meters above sea level. The altitude of a plane is closely related to its elevation, but it specifically refers to the height of the plane above a standard reference level, such as sea level or a specific airport elevation.
The elevation of a plane can have significant effects on its performance and safety. High elevations can reduce the density of the air, which in turn can affect the plane's lift, thrust, and maneuverability. This can be particularly challenging for aircraft taking off or landing at high-altitude airports.
Pilots use a variety of instruments to measure the elevation and altitude of a plane, including radar altimeters, barometric altimeters, and GPS systems. These instruments can provide accurate and real-time information about the plane's position and height above the ground or sea level, helping the pilot to navigate and operate the plane safely.
In summary, elevation refers to the vertical distance above or below a reference point or surface, such as the Earth's surface. In the context of a plane, elevation refers to the height of the plane above or below the ground or sea level. Understanding and monitoring the elevation and altitude of a plane is crucial for safe and efficient flight operations.
We need to find the time when the elevation y is equal to 3600 feet. So, we can set y = 3600 and solve for x.
\(-16x^2\) + 10,000 = 3600
Subtracting 3600 from both sides:
\(-16x^2\) + 6400 = 0
Dividing both sides by -16:
\(x^2\)- 400 = 0
Adding 400 to both sides:
\(x^2\) = 400
Taking the square root of both sides:
x = ±20
Since the skydiver is not going to deploy the parachute before jumping from the airplane, the time must be a positive value. Therefore, x = 20 seconds.
Hence, the skydiver deploys the parachute 20 seconds after jumping from the airplane.
To know more about elevation visit:
brainly.com/question/29477960
#SPJ1
suppose deandre borrows $3000 at an interest rate 2% of compounded each year. assume that no payments are made on the loan. follow the instructions below. do not do any rounding.
a) Find the amount owed at the end of 1 year
b) Find the amount owed at the end of 2 years
Answers
We can use the formula for compound interest: A = P(1 + r/n)^(nt), where A represents the amount owed, P is the principal amount, r is the interest rate.
a) To find the amount owed at the end of the first year, we substitute the given values into the compound interest formula. Since the interest is compounded annually, n = 1. Therefore, the calculation is as follows:
A = 3000(1 + 0.02/1)^(1*1)
A = 3000(1 + 0.02)^1
A = 3000(1.02)
A = 3060
Therefore, the amount owed at the end of the first year is $3060.
b) To calculate the amount owed at the end of the second year, we use the same formula but with t = 2:
A = 3000(1 + 0.02/1)^(1*2)
A = 3000(1 + 0.02)^2
A = 3000(1.02)^2
A = 3000(1.0404)
A = 3121.20
Thus, the amount owed at the end of the second year is $3121.20.
In summary, DeAndre borrows $3000 with a 2% compounded interest rate. Using the compound interest formula, we find that the amount owed at the end of the first year is $3060, and at the end of the second year is $3121.20. The formula takes into account the principal amount, interest rate, compounding frequency, and the number of years to calculate the amount owed.
Learn more about compound interest: brainly.com/question/28020457
#SJP11
A circle has a circumference of 50.24 units.
What is the radius of the circle?
units
Show Calculator
Answers
Answer:
radius = 8 unitsStep-by-step explanation:
Circumference of a circle = 2πr
where
r is the radius
From the question
Circumference = 50.24 units
To find the radius substitute the value into the above formula and solve for the radius
That's
\(50.24 = 2\pi \: r\)
Divide both sides by 2π
We have
\(r = \frac{50.24}{2\pi} \)
r = 7.9959
We have the final answer as
radius = 8 unitsHope this helps you
Answer:
8 units
Step-by-step explanation:
The circumference of a circle is given by
C = 2*pi*r
50.24 = 2 * pi * r
Using 3.14 to approximate pi
50.24 = 2 * 3.14 * r
50.24 = 6.28 r
Divide each side by 6.28
50.24/6.28 = r
8 = r
please i need your help for today please i would really appreciate it

Answers
Answer:80
Step-by-step explanation:
what is the area of the hexagon
answer 1 60.32 cm2 answer 2 74.24 cm answer 3 57.12 cm2 and final answer 46.4 cm2

Answers
what is the equation for the line in slope intercept form PLEASE HELP

Answers
Answer:
y=-4x+5
Step-by-step explanation:
Rewrite \(\frac{200x - 300}{x}\) as a sum of two fractions, and simplify.
Answers
Answer:
We can rewrite this as \(\frac{200x}{x} + \frac{-300}{x}\).
\(\frac{200x}{x}\) simplifies to 200 after eliminating x from the numerator and denominator and \(\frac{-300}{x}\) becomes \(-\frac{300}{x}\) so the final answer is \(200 - \frac{300}{x}\).
Pls help?!?!?! 10 points

Answers
Answer:
I solved it for u!
Hope ot helps!!!

PLEASE HELP ME WITH THESE!!!!!!!!!!!!!!!!!!!!
If I have an answer please ignore my current answer and just solve for the correct answer. Thanksssss!

Answers
The volume of the rectangular prism will be 1008 cubic inches and the volume of the pyramid is 504 cubic inches.
What is volume?The volume of the rectangular prism is defined as the space in three-dimension covered by the rectangular prism having the sides Length, Width, and Height.
The volume of the rectangular prism will be the multiplication of the three parameters which are Length, Width, and Height of the prism.
The volume of the pyramid is the product of half of the area of the base and the height of the pyramid,
The volume of prism = 14 x 12 x 6
The volume of the prism = 1008 cubic inches
The volume of the pyramid,
Volume = 1/2 x Base area x H
Volume = 1/2 x 72 x 14
Volume = 504 cubic inches.
To know more about volume follow
brainly.com/question/24284033
#SPJ1
how to graph x=y^2 on ti-83
Answers
To graph the equation \(x=y^2\) on a TI-83 calculator, you need to follow a few steps. First, go to the "\(Y=\)" screen by pressing the "\(Y=\)" button. Then, enter the equation by typing "\(y^2\)" into the first available function slot. Press the "GRAPH" button to display the graph of the equation on the calculator screen.
To explain the process in more detail, start by turning on your TI-83 calculator and pressing the "\(Y=\)" button, which will take you to the function screen. You'll see a list of function slots labeled "\(Y1\)," "\(Y2\)," and so on. Enter the equation "\(y^2\)" in one of the slots. To enter the squared symbol, press the "^" key, usually located near the upper right corner of the calculator's keypad, followed by "\(2\)." Make sure you use the "\(y\)" variable, which can be found by pressing the "ALPHA" button and then the corresponding letter key. Once you have entered the equation, press the "GRAPH" button to plot the graph on the calculator's screen. The graph should display a parabola opening to the right, representing the equation \(x=y^2\).
By following these steps, you can easily graph the equation \(x=y^2\) on a TI-83 calculator. Remember to check if the graph is within the viewing window and adjust it if necessary using the window settings.
Learn more about graph here:
https://brainly.com/question/17267403
#SPJ11