A tearm scores 96 in 2
matches. Find the rates of scores per match
Answers
The total score in two matches is 96, and you're asked to find the rates of scores per match. If x is the score in the first match and y is the score in the second match, then:x + y = 96 ...(1)But you have no idea what the score of the first match is or what the score of the second match is.
So, we have to find some way to make use of the information we have in the problem. We're looking for the rates of scores per match.The number of matches is not mentioned, so let's assume there are n matches. This implies that the total number of scores (in n matches) would be:n(x + y) = 96n ...(2)If we divide both sides of (2) by n, we get:x + y = 96/nSo, the scores per match are:x/n + y/n = 96/nLet's assume that there were 8 matches. The total score is 96, so the scores per match would be:96/8 = 12Therefore, each match had a score of 12. In general, if there are n matches, then the scores per match would be:96/nFor example, if there were 12 matches, the score per match would be:96/12 = 8Thus, each match would have a score of 8.
To know more about score visit:
https://brainly.com/question/32323863
#SPJ11
Related Questions
Please help ASAP!!!!

Answers
Find the slope-intercept equation of the line containing (1.-4) and having slope m = 3
Answers
Answer:
y=3x-7
Step-by-step explanation:
HELPPP WHAT IS THE ANSWER DONT SENT A FILE PLZ EXPLAIN STEP BY STEP PLZ I DINT HAVE A LOT OF TIME
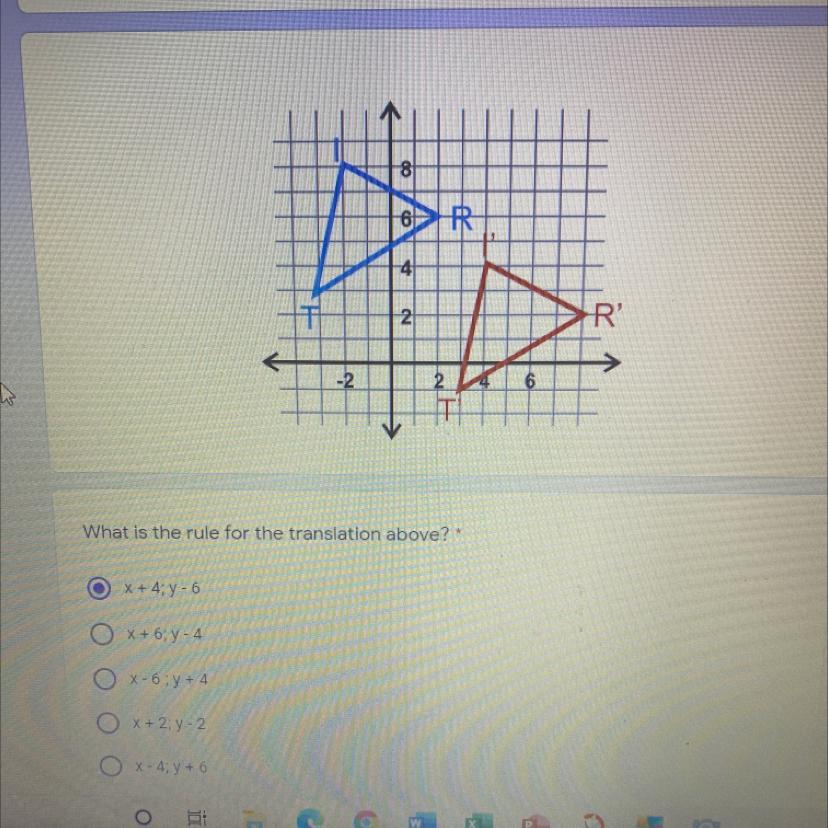
Answers
Answer:
2nd option
Step-by-step explanation:
Consider the coordinates of T(- 3, 3 ) → T' (3, - 1 )
- 3 → 3 is 6 units right in the positive x-direction
3 → - 1 is 4 units down in the negative y- direction
Then translation rule is
(x, y ) → (x + 6, y - 4 )
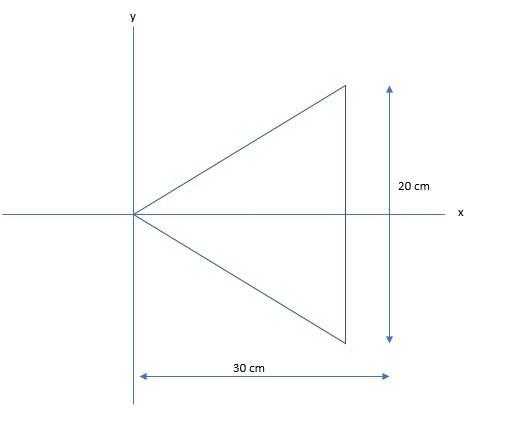
an 800 g steel plate has the shape of the isosceles triangle shown in the figure(figure 1).
Answers
The x- and y-coordinates of the center of mass are; (20, 0)
What is the center of mass of an object?The center of mass is the location where the sum of the relative position of the masses in a mass distribution is zero. It is the point where force can be applied on the distributed mass without causing a rotation of the system.
The mas of the steel plate = 800 g = 0.8 kg
The base length of the isosceles triangular plate = 20 cm = 0.2 m
The height of the isosceles triangular plate = 30 cm = 0.3 m
Considering a small strip of height, dx and width, I, we get
Area of small strip, dA = I·dx
Density of the plate for a unit thickness, ρ = M/A
Density of the small strip of mass dm = dm/dA
Considering the density of the plate as uniform, we get;
\(\displaystyle {\frac{dm}{dA} =\frac{M}{A}\)
Therefore;
\(\displaystyle {dm=\frac{M}{A}\times dA}\)
The area of the triangular plate, A = (1/2) × 0.2 m × 0.3 m = 0.03 m²
Mass of the plate, M = 0.8 kg
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx}\)
The width of the small strip, I, located at a distance x from the vertex of the triangular plate, using similar triangles, indicates;
\(\dfrac{I}{20} = \dfrac{x}{30}\)
\(I=20\times \dfrac{x}{30} = \dfrac{2}{3} \cdot x\)
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx} = \frac{0.8}{0.03}\times \dfrac{2}{3} \cdot x\cdot dx}\)
The center of mass, \(x_{cm}\), can be obtained with the formula; \(\displaystyle {x_{cm} = \dfrac{1}{M} \cdot \int\limits {x} \, dm }\)
Therefore; \(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx }\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx } = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0\)
\(\displaystyle {x_{cm} = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0=\frac{200}{9} \times \frac{0.027}{3} =0.2\)
The location of the x-coordinate center of mass, \(x_{cm}\) = 0.2 m = 20 cm from the vertex, which is the same location as the x-coordinate of the centroid of the plate of uniform density.
The plate is symmetrical about the x-axis, therefore, the y-coordinate of the center of mass is along the x-axis, which is \(y_{cm}\) = 0
The coordinate of the center of mass = (0.2, 0)
Part of the question requires the location of the coordinate of the center of mass of the triangular plate
Learn more about the center of mass of regular shapes here:
https://brainly.com/question/28021242
#SPJ1

Can anyone help me with this question?
Given that X = [3, 5) and Y = (4, 9). Find A ∪ B
Answers
Answer:
A ∪ B = [3, 9)
Step-by-step explanation:
Set X is 3, and all number greater than 3 up, but not including, 5.
Set Y is all numbers from 4 to 9, but not including 4 or 9.
The union of the sets is all numbers from 3 up to 9, including 3 but not including 9.
A ∪ B = [3, 9)
Comparing two algorithms.
Say we have two different algorithms with respective runtimes of f(n) and g(n). Given the following cases, prove whether or not f(n) = ϴ(g(n)) is true in each case. Show your work but with the crucial steps only. P.S. sqrt(n) means the square-root of n, aka n^(½).
Case
f(n)
g(n)
A
log(n^200)
log(n^2)
B
sqrt(n)
log(n)
C
3^n
5^n
D
sin(n)+3
cos(n)+1
Answers
f(n) = ϴ(g(n)) is not true in cases B(sqrt(n)log(n), C(\(3^n 5^n\)), and D(sin(n)+3 cos(n)+1).
A) \(log(n^200) log(n^2)\)
Here, f(n) = \(log(n^200)\) and g(n) = \(log(n^2)\). Now, if we take the limit of f(n) / g(n) as n approaches infinity, then:
f(n) / g(n) = \([log(n^200) / log(n^2)]\) = 100
This means that as n approaches infinity, the ratio f(n) / g(n) is constant, and so we can say that f(n) = ϴ(g(n)). Therefore, f(n) = ϴ(g(n)) is true in this case.
B) sqrt(n) log(n) Here, f(n) = sqrt(n) and g(n) = log(n). Now, if we take the limit of f(n) / g(n) as n approaches infinity, then:
f(n) / g(n) = [sqrt(n) / log(n)]
As log(n) grows much slower than sqrt(n) as n approaches infinity, this limit approaches infinity. Therefore, we cannot say that f(n) = ϴ(g(n)) is true in this case.
C) 3^n 5^n
Here, f(n) = \(3^n\) and g(n) = \(5^n\) . Now, if we take the limit of f(n) / g(n) as n approaches infinity, then:
f(n) / g(n) = \([3^n / 5^n]\)
As \(3^n\) grows much slower than \(5^n\) as n approaches infinity, this limit approaches zero. Therefore, we cannot say that f(n) = ϴ(g(n)) is true in this case.
D) sin(n) + 3 cos(n) + 1
Here, f(n) = sin(n) + 3 and g(n) = cos(n) + 1. Now, if we take the limit of f(n) / g(n) as n approaches infinity, then:
f(n) / g(n) = [sin(n) + 3] / [cos(n) + 1]
As this limit oscillates between positive and negative infinity as n approaches infinity, we cannot say that f(n) = ϴ(g(n)) is true in this case.
Therefore, f(n) = ϴ(g(n)) is not true in cases B, C, and D.
To know more about log refer here:
https://brainly.com/question/32621120
#SPJ11
Mathematical 3r take away 5 = 16
Answers
Answer:
r = 7
Step-by-step explanation:
Given
3r - 5 = 16 ( add 5 to both sides )
3r = 21 ( divide both sides by 3 )
r = 7
x+y=16
y=3x=4
find the solution using substitution
Answers
Answer: x=3 ; y=13
Step-by-step explanation:
1. isolate y from equation to substitute into the second equation
y= 16-x ---> (16-x) = 3x+4
2. move to one side and solve for x
4x=12 --> x=3
3. plug in x value to solve for y
3+y=16 or 3(3)+4
y=13
Five students want to play dodgeball and they all want to be a team captain. To be fair, the gym coach decides to place the names of all five students into a hat, mix well, and select two names at random without replacement. The names chosen will be the team captains. Each outcome in the sample space for the random selection of two team captains is equally likely. What is the probability of each outcome in the sample space? startfraction 1 over 25 endfraction startfraction 1 over 20 endfraction startfraction 1 over 10 endfraction one-fifth.
Answers
The probability of each outcome in the sample space is B. 1/20.
What is probability?Probability means possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one.
For given example, the total number of students:n(S) = 5. The probability of selecting one student would be: P(A) = 1/5.
Now, there are 4 students.n(S) = 4
So, probability of selecting second student from remaining 4.P(B) = 1/4
Hence, the probability of each outcome in the sample space would be:
1/5 × 1/4
= 1/20
Therefore, the probability of each outcome in the sample space is 1/20.
Learn more about the probability at:
https://brainly.com/question/25870256
#SPJ1
The seeds in bush bean pods are each the product of an independent fertilization event. Green seed color is dominant to white seed color in bush beans. If a heterozygous plant with green seeds self-fertilizes, what is the probability that 6 seeds in a single pod of the progeny plant will consist o 5 green and 1 white seeds
Answers
The probability of getting 5 green seeds and 1 white seed in a single pod is 0.25 or 25%.
In bush beans, green seed color is dominant to white seed color. If a heterozygous plant with green seeds (Gg) self-fertilizes, we can use the principles of Mendelian genetics to determine the probability of obtaining 6 seeds in a single pod with 5 green and 1 white seed.
When the plant self-fertilizes, each seed in the pod receives one allele from the mother plant (G) and one allele from the father plant (g). Since the plant is heterozygous (Gg), there are two possible combinations of alleles that can result in a white seed: Gg or gg. The probability of getting a white seed is equal to the probability of inheriting the gg combination.
To calculate the probability, we can use a Punnett square. When a heterozygous plant self-fertilizes, the Punnett square shows that there is a 25% chance (1 out of 4 possible combinations) of obtaining a white seed (gg). Therefore, the probability of getting 5 green seeds and 1 white seed in a single pod is 0.25 or 25%.
It is important to note that this probability assumes that the inheritance of seed color follows Mendelian genetics and that there are no other factors influencing the expression of seed color in bush beans.
Know more about probability here:
https://brainly.com/question/30034780
#SPJ11
Three rugs have a combined area of 2200m^2 . By overlapping the rugs to cover a floor area of 140m^2 , the area which is covered by exactly two layers of rug is 24m^2 . What area of floor is covered by three layers of rug
Answers
Let the areas of the three rugs be a, b, and c. Then according to the given information, a + b + c = 2200Also, area of overlap of the rugs (covered by exactly two layers of rug) = 24m²Hence, (a + b + c) – 2(area covered by two layers of rug) = area covered by three layers of rug (2200 – 2 × 24)m² = 2152m².
Therefore, area covered by three layers of rug is 2152m². Three rugs have a combined area of 2200m^2 . By overlapping the rugs to cover a floor area of 140m^2 , the area which is covered by exactly two layers of rug is 24m^2 . What area of floor is covered by three layers of rug Three rugs have a combined area of 2200m^2 . By overlapping the rugs to cover a floor area of 140m^2 , the area which is covered by exactly two layers of rug is 24m^2 .
What area of floor is covered by three layers of rug. Let the areas of the three rugs be a, b, and c. Then according to the given information, a + b + c = 2200Also, area of overlap of the rugs (covered by exactly two layers of rug) = 24m²Hence, (a + b + c) – 2(area covered by two layers of rug) = area covered by three layers of rug (2200 – 2 × 24)m² = 2152m².
To know more about areas visit:
https://brainly.com/question/30307509
#SPJ11
(q55) When evaluating
, what should you substitute for u?

Answers
When evaluating the integral ∫ tan³x sec⁵x dx you should substitute u = sec x.
option C.
What should you substitute for u?The integral of the function ∫ tan³x sec⁵x dx is determined by applying substitution method as follows;
Let u = sec x
du/dx = sec x tan x
We will substitute the value of u and solve for the integral.
∫ tan³x sec⁵x dx = ∫ tan³x (sec x)⁵ (du / (sec x tan x))
∫ tan³x sec⁵x dx = ∫ tan³x sec⁴x du
u = sec x, so sec⁴x = u⁴
∫ tan³x sec⁵x dx = ∫ tan³x u⁴ du
So we can conclude that, when evaluating the integral ∫ tan³x sec⁵x dx you should substitute u = sec x
Learn more about integral here: https://brainly.com/question/30215870
#SPJ1
P-18=3 solve for P??
Answers
Answer:
P=21
Step-by-step explanation:
The solution to the equation P - 18 = 3 for P is P = 21
How to determine the solution to the equation for PFrom the question, we have the following parameters that can be used in our computation:
P - 18 = 3
Add 18 to both sides of the equation
so, we have the following representation
18 + P - 18 = 3 + 18
Evaluate the like terms on the right hand side
This gives
18 + P - 18 = 21
Evaluate the like terms on the left hand side
This gives
P = 21
Hence. the solution is 21
Read more about equations at
https://brainly.com/question/32492977
#SPJ6
If the graph of the function f, defined by f(x)= x2 + 5, is translated vertically upward by 2 units, it
becomes the graph of a function k. Find the expression for k(x).
A. k(x)=x2 + 3
B. k(x)=(x + 2)2 +5
C. k(x)=(x - 2)2 +5
D. k(x)= x2 +7
Answers
Answer:
D. k(x)=x²+7
Step-by-step explanation:
f(x)=x² + 5
y=mx+c
since it is not moved horizontally the x and slope(m) will remain the same but the 2 will be added to the intercept(c) which is 5 to become seven
Can you explain how you solved this?

Answers
Set 3x-4 equal to -3 then solve for x
Like this: 3x-4=-3
Then plug the answer in (1/3) in for x in the next equation and solve
Help please I need this done

Answers
Step-by-step explanation:
the answer is in the above image

Answer:
61°
Step-by-step explanation:
(x+18)°=(4x-15)°alternate angles, because BC is parallel to AD
x°+18°=4x°-15°
18°+15°=4x°-x°
33°=3x°
33°/3°=3x°/3°
11=x
angle ABD
90°-(x+18)°. the sides of a rectangle meet at 90°
90°-(11+18)°
90°-(29)°
90°-29°
61°
When a
-5and b
3, the value of the expression is __
Answers
the correct answer is 8
I will do anything for a legit answer plsssssss
The tennis team is having a fundraiser for uniforms for its 9 players. The total cost for the uniforms is $759.84 and the team already has $224.36. Write and solve an inequality that represents the amount of money, x, each team member must raise? Input your answer as an inequality with no spaces
Answers
Answer:
X ≥ 59.50
Step-by-step explanation:
So to begin, your equation would need to solve for x. X has to be greater than or equal to the minimum amount each player needs to raise for the uniforms. To find how much money they need to raise subtract $224.36 from $759.84 to get $535.48. Divided $535.48 by 9 players to see the minimum amount they each need to contribute. You should get $59.50 roughly. So each player would need to raise greater than or equal to $59.50.
Hope this helps!
The scatter plot below shows nine points from a data set. 12.0 10.8 9.6 8.4 7.2 6.0 4.8 3.6 2.4 1.2 ● 0 1 2 3 4 5 6 7 8 9 10
A 4,4,5,5,6,6
b 4,10,4,11,4,12
C8,9,8,10,8,11
D10,10,10,11,10,12
Answers
Answer:
Therefore, based on the given scatter plot, the set of numbers that matches the points is C. 8,9,8,10,8,11.
Step-by-step explanation:
The scatter plot shown represents a set of nine points on a coordinate plane. Each point consists of an x-coordinate and a y-coordinate. To determine which set of numbers corresponds to the scatter plot, we need to analyze the pattern in the given points.
Looking at the scatter plot, we observe that the x-coordinates range from 0 to 10 with an increment of 1, while the y-coordinates seem to vary.
Now let's examine the given answer choices:
A. .4,4,5,5,6,6
B. .4,10,4,11,4,12
C. 8,9,8,10,8,11
D. 10,10,10,11,10,12
Set C (8,9,8,10,8,11) among these answer choices matches the pattern observed in the scatter plot. The x-coordinates in the scatter plot range from 0 to 10, and the y-coordinates correspond to the numbers provided in set C.
Therefore, based on the given scatter plot, the set of numbers that matches the points is C.
For more questions on this topic refer to this link:
https://brainly.com/question/6592115
#SPJ8
Justin runs each lap in 8 minutes. He will run at least 6 laps today. What are the possible numbers of minutes he will run today?
Use t for the number of minutes he will run today.
Write your answer as an inequality solved for t.
Answers
Answer:
48 minutes
Answer:
48
Evaluate the following integral. * >) In? (x²) dx X dx=(Type an inte х Help me solve this Vio
Answers
The value of the integral\(\int\limits^{e^{5}}_0 {ln^{2}(x^{2})/x} \, dx\) = 2(x²) ln(x²)² - 2(x²) ln(x²) + 2(x²) + C, where C is the constant of integration.
To evaluate the integral ∫₀^(e⁵) (ln²(x²)/x) dx, we can use a substitution. Let's set u = x², then du = 2x dx. Rearranging, we have dx = du/(2x). Substituting these into the integral, we get:
\(\int\limits^{e^{5}}_0 {ln^{2}(x^{2})/x} \, dx\) dx = ∫₀^(e⁵) (ln²(u)/(2x)) du/(2x)
= 1/4 ∫₀^(e⁵) (ln²(u)/u) du
Now, let's focus on the integral ∫₀^(e^5) (ln²(u)/u) du. We can integrate this by parts twice. The formula for integration by parts is ∫u dv = uv - ∫v du.
Let's choose:
u = ln²(u) --> du = 2ln(u) / u du
dv = du/u --> v = ln(u)
Using integration by parts, we have:
\(\int\limits^{e^{5}}_0 {ln^{2}(x^{2})/x} \, dx\) = ln²(u) * ln(u) - ∫2ln(u) * ln(u) du
Let's integrate the remaining term:
∫2ln(u) * ln(u) du = 2 ∫ln²(u) du
We can use integration by parts again:
u = ln(u) --> du = (1/u) du
dv = ln(u) --> v = u ln(u) - u
Applying integration by parts, we have:
2 ∫ln²(u) du = 2 (ln(u) * (u ln(u) - u) - ∫(u ln(u) - u) (1/u) du)
= 2 (ln(u) * (u ln(u) - u) - ∫(ln(u) - 1) du)
= 2 (ln(u) * (u ln(u) - u) - u ln(u) + u) + C
= 2u ln(u)² - 2u ln(u) + 2u + C
Now, substituting back u = x², we have:
\(\int\limits^{e^{5}}_0 {ln^{2}(x^{2})/x} \, dx\)= 2(x²) ln(x²)² - 2(x²) ln(x²) + 2(x²) + C
Therefore, the value of the integral ∫₀^(e⁵) (ln²(x²)/x) dx is:\(\int\limits^{e^{5}}_0 {ln^{2}(x^{2})/x} \, dx\) = 2(x²) ln(x²)² - 2(x²) ln(x²) + 2(x²) + C, where C is the constant of integration.
To know more about integral check the below link:
https://brainly.com/question/27419605
#SPJ4
Incomplete question:
Evaluate the following integral.
\(\int\limits^{e^{5}}_0 {ln^{2}(x^{2})/x} \, dx\)
Tanya painted a mural that was 8 feet tall. The area of the mural was 224 square feet. What is the length of Tanya’s mural?
I owe you 90 just help me...
Answers
The length of the Mural is 28 feet
Area of mural which is a rectangle= length x height
which gives 224 = length x 8
which gives length= 224/8
and gence lentgh of mural = 28 feet
what is the probability that an emotional health index scores is less than 80.2 givrn that it is already less than 81
Answers
The probability that an emotional health index score is less than 80.2 given that it is already less than 81 is approximately 0.141
Let A be the event that the emotional health index score is less than 80.2, and let B be the event that the emotional health index score is less than 81. Then we want to find P(A|B), the probability of A given that B has occurred.
We can use Bayes' theorem to find this probability:
P(A|B) = P(B|A) × P(A) / P(B)
where P(B|A) is the probability of B given that A has occurred, P(A) is the probability of A, and P(B) is the probability of B.
From the given data, we know that the emotional health index scores are normally distributed with a mean of 82.6 and a standard deviation of 6.8. Therefore, we can find the probabilities of A and B using the normal distribution:
P(A) = P(X < 80.2) = 0.019
P(B) = P(X < 81) = 0.135
where X is a normally distributed random variable with mean 82.6 and standard deviation 6.8.
To find P(B|A), we need to find the probability that the score is less than 81 given that it is less than 80.2. This probability can be found using the conditional probability formula:
P(B|A) = P(A and B) / P(A)
We can assume that the scores are distributed normally with the given mean and standard deviation. Then, we can use the standard normal distribution to find the probabilities:
P(X < 80.2) = (80.2 - 82.6) / 6.8 = -0.353
P(X < 81) = (81 - 82.6) / 6.8 = -0.235
The probability of A and B can be found by finding the probability of A and multiplying it by the conditional probability of B given A:
P(A and B) = P(X < 80.2 and X < 81)
= P(X < 80.2)
= 0.019
Therefore,
P(B|A) = P(A and B) / P(A)
= 0.019 / 0.019
= 1
Now we can use Bayes' theorem to find P(A|B):
P(A|B) = P(B|A) × P(A) / P(B)
= 1 × 0.019 / 0.135
= 0.141
Learn more about conditional probability here
brainly.com/question/30144287
#SPJ4
The given question is incomplete, the complete question is:
what is the probability that an emotional health index scores is less than 80.2 given that it is already less than 81?

I need help on two questions here’s the first one!
Antawn wrote a decimal. The value of the 8 in Antawn’s decimal is equal to 8 x 1/10. Which of the following numbers could be Antawn’s decimal?
A. 86.05
B. 68.05
C. 60.85
D. 60.58
Here’s the second question!
Brooklyn rode her bike a total of 75.8 miles in 3 days. She rode 25.2 miles on Friday and 16.9 miles on Saturday. How many miles does she ride her bike on Sunday?
A. 33.7
B. 34.7
C. 42.1
D. 117.9
Answers
Answer:
these are what I ythink the answers are
1) C
2)A
For 1. the answer is B
The area of a square is a function of the length of the side of the square.
Answers
Answer: A =a2
Step-by-step explanation:
the experiment involved tossing three coins simultaneously. the experiment was carried out 100 times, and it was noted that three heads occurred 40 times. what is the difference between the experimental probability of getting three heads and its theoretical probability? write the answer in the simplest form of fraction.(1 point)
Answers
The difference between the experimental probability of getting three heads and its theoretical probability is 11/40.
To find the difference between the experimental probability and the theoretical probability of getting three heads when tossing three coins simultaneously, we need to calculate both probabilities and subtract them.
The theoretical probability is determined by considering all possible outcomes and their likelihood.
When tossing three coins, there are 2³ = 8 possible outcomes since each coin can land either heads or tails.
Out of these 8 outcomes, only one outcome results in three heads.
The theoretical probability of getting three heads is therefore 1/8.
The experimental probability is determined by conducting the actual experiment and recording the observed outcomes.
The experiment was carried out 100 times, and three heads occurred 40 times.
The experimental probability of getting three heads is therefore 40/100 or 2/5.
To find the difference between the experimental probability and the theoretical probability, we subtract the theoretical probability from the experimental probability:
Experimental probability - Theoretical probability = 2/5 - 1/8
To simplify this fraction, we need to find a common denominator:
2/5 - 1/8 = (16/40) - (5/40)
= 11/40
For similar questions on theoretical probability
https://brainly.com/question/8652467
#SPJ8
how do find the √27 between? How can you solve without a calculator?
Answers
True or False? A circle could be circumscribed about the quadrilateral below.

Answers
Answer:
false
Step-by-step explanation:
Because the length of the sides are not the same
use power series operations to find the taylor series at x0 for the following function. x^3tan^-1x^2
Answers
Taylor series for x^3tan^-1x^2 at x0 = 0 can be found by using the power series operations. The Taylor series for x^3tan^-1x^2 at x0 = 0 is:
x^3tan^-1x^2 = x^3(x^2 - (x^2)^3/3 + (x^2)^5/5 - ...)
To find the Taylor series, we need to express the function as a sum of terms with powers of (x - x0). We can start by using the power series for tan^-1x:
tan^-1x = x - x^3/3 + x^5/5 - ...
Then, we substitute x^2 for x and multiply by x^3 to get:
x^3tan^-1x^2 = x^3(x^2 - (x^2)^3/3 + (x^2)^5/5 - ...)
This gives us the Taylor series for x^3tan^-1x^2 at x0 = 0.
We can simplify the expression by expanding the powers of x:
x^3tan^-1x^2 = x^5 - x^7/3 + x^9/5 - ...
This means that the function can be approximated by the sum of these terms, which become more accurate as we include more terms. The Taylor series can be useful for approximating functions and making calculations easier, especially when using computers to perform calculations.
To learn more about Taylor series, click here: brainly.com/question/30772973
#SPJ11
AABC has vertices at A(1, -9), B(8, 0), and C(9, Is AABC an equilateral triangle? Justify your answer. Yes, all sides are congruent.
Yes, BC is congruent to AC.
No, BC is not congruent to AC. 8).
No, AB is not congruent to AC.
Answers
The correct statement regarding whether the triangle is equilateral is given as follows:
No, AB is not congruent to AC.
What is an equilateral triangle?An equilateral triangle is a triangle in which all the side lengths have the same measure.
Given the coordinates of the side lengths, we use the formula for the distance between two points to obtain the side lengths.
For example, the length AB is given as follows:
AB = sqrt([8 - 1]² + [-9 - 0]²)
AB = sqrt(130).
The length AC is given as follows:
AC = sqrt([1 - 9]² + [-9 - 8]²)
AC = sqrt(353).
AB is different of AC, hence the triangle is not equilateral.
More can be learned about equilateral triangles at https://brainly.com/question/1058720
#SPJ1