An account paying 4. 6% interest compounded quarterly has a balance of $506,732. 32. Determine the amount that can be withdrawn quarterly from the account for 20 years, assuming ordinary annuity. A. $9,722. 36 b. $6,334. 15 c. $23,965. 92 d. $7,366. 99.
Answers
The amount that can be withdrawn quarterly from the account for 20 years, assuming ordinary annuity, is approximately $6,334.15.
To determine the amount that can be withdrawn quarterly from the account, we need to use the formula for the future value of an ordinary annuity:
FV=P×(( \((1+r)^{n}\)-1)/r)
Where:
FV = Future value of the annuity
P = Amount withdrawn each period
r = Interest rate per period
n = Number of periods
In this case, the interest rate is 4.6% per year, compounded quarterly. To find the interest rate per quarter, we divide the annual interest rate by the number of compounding periods in a year:
r=4.6/4 = 1.15%
The number of periods is 20 years multiplied by the number of compounding periods in a year:
n=20*4=80
Now, we can substitute the given values into the future value formula:
506,732.32=P×((\((1+0.0115)^{80}\)-1)/0.0115)
Solving for P, we find:
Using a calculator, we obtain P ≈ $6,334.15. Therefore, the amount that can be withdrawn quarterly from the account for 20 years, assuming ordinary annuity, is approximately $6,334.15. Therefore, the correct answer is option b.
Learn more about amount here:
https://brainly.com/question/21641119
#SPJ11
Related Questions
What is the lcm of 150 and 180
Answers
Answer:
900
Step-by-step explanation:
multiply 2x2x3x3x5x5
4x9x25 which is 900

solution a coin is flipped three times. let e be the event that heads and tails occur at least once each and let f be the event that heads occurs at least twice. are e and f independent events?
Answers
According to given condition, E and F are independent events.
To determine if events E and F are independent, we need to check if the occurrence of one event affects the probability of the other event.
Let's first calculate the probability of event E, which is the probability of getting at least one head and one tail in three coin flips. We can use the complement rule to find the probability of the complement of E, which is the probability of getting all heads or all tails in three coin flips:
P(E) = 1 - P(all heads) - P(all tails)
P(E) = 1 - \((1/2)^{3}\) - \((1/2)^{3}\)
P(E) = 3/4
Now, let's calculate the probability of event F, which is the probability of getting at least two heads in three coin flips. We can use the binomial distribution to find the probability of getting two or three heads:
P(F) = P(2 heads) + P(3 heads)
P(F) = (3 choose 2)\((1/2)^{3}\) + \((1/2)^{3}\)
P(F) = 1/2
To check if E and F are independent, we need to calculate the joint probability of E and F and compare it to the product of the probabilities of E and F:
P(E and F) = P(at least one head and one tail, at least two heads)
P(E and F) = P(2 heads) + P(3 heads)
P(E and F) = (3 choose 2)\((1/2)^{3}\)
P(E and F) = 3/8
P(E)P(F) = (3/4)(1/2)
P(E)P(F) = 3/8
Since the joint probability of E and F is equal to the product of their individual probabilities, we can conclude that E and F are independent events. In other words, the occurrence of one event does not affect the probability of the other event.
To learn more about independent events here:
https://brainly.com/question/30905572
#SPJ4
Pls someone help me in this question
Select yes or no to indicate whether each of the ordered pairs is most likely a solution to the equation represented by the graph
(0,0) Yes or no
(1,1) Yes or no
(-1,4) Yes or no

Answers
Answer:
no
no
yes
Step-by-step explanation:
The frequency table shows how many visits to the library students in a school have made in the last month.
Visits Frequency
0 284
1 218
2 76
3 64
4 42
5 320
Work out the mean.
Give your answer rounded to 1 DP.
Answers
A mean is an arithmetic average of a set of observations. The mean number of visits the students made to the library in the last month is 2.32 visits.
What is Mean?A mean is an arithmetic average of a set of observations. it is given by the formula,
Mean = (Sum of observations)/Number of observations
For the given frequency table, the sum of the mean and the total number of values can be written as,
Sum = (0×284) + (1×218) + (2×76) + (3×64) + (4×42) + (5×320) = 2330
Total number of values = 284 + 218 + 76 + 64 + 42 + 320 = 1004
The mean for the table can be written as,
Mean = sum/ Total number of values = 2330/1004 = 2.32
Hence, the mean number of visits the students made to the library in the last month is 2.32 visits.
Learn more about Mean:
https://brainly.com/question/16967035
#SPJ1
Two numbers have a product of −24 and a difference of 11. What are the two numbers?
Answers
Answer:
-8 and 3, or -3 and 8
Step-by-step explanation:
xy = -24
x - y = 11
x = y + 11
y(y + 11) = -24
y^2 + 11x + 24 = 0
(y + 8)(y + 3) = 0
y = -8 or y = -3
x = 3 or x = 8
the numbers are -8 and 3, or -3 and 8
QUESTION 2 . 1. 40 earrings. She then sells each pair for R30. Mpho is selling earrings. She spends R200 for the material to make INSPIRED BY THE BEAUTY OF AN AFRICAN WOMAN! 2.1.1. Calculate the selling price of each earring?
Answers
Answer:
R200
Step-by-step explanation:
selling price of each earring
R200
Question (Multiple Choice Wor (07.01) Which of the values in the set {3,4,5,6) is a solution to the equation 4x + 2 = 22? 3 4 5 6
Answers
Answer:
4x+2=22
4x+2-2=22-2
4x=20
4x/4=20/4
x=5
Could anyone help please

Answers
Answer:
T=.25k+.97t
This is because you 25 cents of gas is multiplied by k, which leaves the other section of the equation.
In the diagram below, ABC ~ DEC. What is the value of x?
A. 2
B. 3.5
C. 2.5
D. 3

Answers
5x=18-x
6x=18
x=3
Answer is (D).
Answer:
x = 3
Step-by-step explanation:
Please refer to the attached photo. (Apologies for the terrible drawing.)
Since we know triangles ABC and DEC are similar, we can use the ratio method to find x.
\( \frac{ec}{bc} = \frac{ed}{ba} \\ \frac{25}{5} = \frac{18 - x}{x} \\ \frac{18 - x}{x} = 5 \\ 18 - x = 5x \\ 18 = 5x + x \\ 6x = 18 \\ x = \frac{18}{6} \\ = 3\)

Can someone please help me!!

Answers
Multiplication is the process of multiplying. Jay lost 30 pounds in a period of 6 months.
What is multiplication?Multiplication is the process of multiplying, therefore, adding a number to itself for the number of times stated. For example, 3 × 4 means 3 is added to itself 4 times, and vice versa for the other number.
A.) The newly recorded temperature in January will be six times the temperature in February, therefore, we can write,
January = 6 × February = 6×(-3°F) = -18°F
Hence, the newly recorded temperature in January will be equal to -18°F.
B.) Change in water level on each day of the drought was equal to -4 inches, while the drought lasted for 1 week(7days), Thus, the net change in water level can be written as,
net change = 7 × -4 = -28inches
Hence, the net change in the water level during the drought was equal to -28 inches.
C.) Jay went on a diet for six months and lost 5 pounds each month, therefore, the net change in the weight will be equal to,
Net Change = 6 × 5 = 30 pounds
Hence, Jay lost 30 pounds in a period of 6 months.
Learn more about Multiplication:
https://brainly.com/question/14059007
#SPJ1
If one side of a triangle increases by 11cm and the other side decreases by the same value, we get an equilateral triangle. When the first side is multiplied by 4, it is 10cm longer than 3 times the third side. Find the length of of the longest side of the original triangle.
Answers
Answer:
Length of the longest side: 65 cm
Step-by-step explanation:
First side = x;
"Other side (with respect to first side)" = y;
Third side = z
When the first side is multiplied by 4, it is 10cm longer than 3 times the third side : 4x = 10 + 3z
We receive an equilateral triangle when one side increases by 11, and the other decreases by 11. Therefore when x + 11, and y - 11, x + 11 = z, and y - 11 = z.
x + 11 = z x - z = 11
y - 11 = z → y - z = 11
4x = 10 + 3z 4x - 3z = 10
Matrix:
\(\begin{bmatrix}1&-1&0&|&-11\\ 0&-1&1&|&11\\ 4&-3&0&|&10\end{bmatrix}\)
If we reduce this matrix, our dimensions are 43, 54, and 65. Therefore the length of the longest side of the original triangle would be 65.
The sides of an equilateral triangle are equal.
The longest side of the original triangle is 65 cm
Let the sides of the original triangle be a, b and c.
From the question, we have:
\(\mathbf{4a = 10 + 3c}\) --- the first side multiplied by 4, is 10 more than the third side multiplied by 3
The equations that relate the increment or decrement of the side lengths are:
\(\mathbf{a + 11 = c}\)
\(\mathbf{b - 11 = c}\)
Make a, the subject in \(\mathbf{a + 11 = c}\)
\(\mathbf{a = c - 11}\)
Substitute \(\mathbf{a = c - 11}\) in \(\mathbf{4a = 10 + 3c}\)
\(\mathbf{4(c - 11) = 10 + 3c}\)
Open brackets
\(\mathbf{4c - 44 = 10 + 3c}\)
Collect like terms
\(\mathbf{4c - 3c = 10 + 44}\)
\(\mathbf{c = 54}\)
Recall that: \(\mathbf{a = c - 11}\)
So, we have:
\(\mathbf{a= 54 - 11}\)
\(\mathbf{a= 43}\)
Also, recall that: \(\mathbf{b - 11 = c}\)
So, we have:
\(\mathbf{b - 11 = 54}\)
\(\mathbf{b = 11 + 54}\)
\(\mathbf{b = 65}\)
So, we have:
\(\mathbf{a= 43}\)
\(\mathbf{b = 65}\)
\(\mathbf{c = 54}\)
By comparing the side lengths, we have:
The longest side of the original triangle is 65 cm
Read more about equilateral triangles at:
https://brainly.com/question/3461022
Cassandra's money that she makes from selling cookies can be determined by the equation y = 2X -
20. To not lose money she has to sell over 10 cookies per day but she only makes a batch of 15
cookies each day. What is the range in this situation if she does not lose money?
Answer choices shown in picture. Please help! I put 45 points and i’ll give you a brainliest if it’s correct!
Answers
Answer:
E
Step-by-step explanation:
Because the y-intercept is (0,-20)
please this is half my grade!!!
Benjamin has a ladder that is 15 ft long. He wants to lean the ladder against a vertical wall so that the top of the ladder is 13.8 ft above the ground. What is the angle, rounded to the nearest tenth, that the ladder makes with the ground? Show your work
2. What is the length of side YZ to the nearest tenth? Show your work.
side XY is 11 feet, and angle Z is 35 degrees(this is a right triangle)
3. What are the exact measures of the other two sides of the triangle? Use special right triangles ratios and show your work.
Side AC is 14 feet, this is a right triangle, and angle A is 30 degrees
Answers
The special right triangle is the right triangle that have acute angle values
that simplify the process of finding its dimensions.
The correct values are;
1. The angle the ladder makes with the ground, is approximately 66.93°
2. The length of YZ is approximately 19.18 ft.
3. CB = 7 ft. and AB = 7·√3 ft.
Reasons:
1. The length of the ladder = 15 ft.
Height of the ladder above the ground, h = 13.8 ft.
Required:
The angle the ladder makes with the ground.
Solution:
The angle the ladder makes with the ground is given by the equation;
\(sin(\theta) = \dfrac{Length \ of \ the \ ladder}{Height\ of \ the \ ladder \ above the \ ground} = \dfrac{13.8}{15} = 0.92\)
\(\theta = arcsin\left(0.92 \right) \approx 66.93^{\circ}\)
2. The given parameters are;
XY = 11
∠Z = 35°
YZ = Required
In a right triangle, the side facing the acute angle is a leg of the triangle.
Therefore;
XY is the opposite side to ∠Z
\(sin(\angle Z) = \dfrac{XY}{YZ}\)
Which gives;
\(sin(35^{\circ}) = \dfrac{11}{YZ}\)
\(YZ= \dfrac{11}{sin(35^{\circ}) } \approx 19.18\)
YZ ≈ 19.18 ft.
3. AC = 14 ft.
∠A = 30
Required:
The length of the other two sides
Solution:
Where by AC is the hypotenuse side, we have;
CB = AC × sin(∠A)
Therefore;
CB = 14 × sin(30°) = 7
CB = 7 ft.
AB = AC × cos(∠A) = 14 × cos(30°) = 7·√3
Learn more here:
https://brainly.com/question/12237712
1. The angle the ladder makes with the ground, is approximately 66.93°
2. The length of YZ is approximately 19.18 ft.
3. CB = 7 ft. and AB = 7·√3 ft.
on friday, terry completes a self-monitoring scale and receives a score of 49. on the following tuesday, he fills out the scle again and receives a score of 28. terry's scores on this self-monitoring scale do not appear to be
Answers
If on the following Tuesday, Terry fills out scale again and receives a score of 28 , then Terry's scores on the Self-Monitoring Scale do not appear to be Reliable .
The Terry's scores on the Self-Monitoring Scale do not appear to be reliable, because there is a significant difference between his score on Friday and his score on the following Tuesday.
The Reliability is defined as the consistency of measurement over time or across different conditions.
In this case, if Terry's scores on the Self-Monitoring Scale were reliable, we would expect them to be consistent or stable over time.
However, his score on Tuesday is significantly lower than his score on Friday suggests that there may be some inconsistency in his responses .
Learn more about Self Monitoring Scale here
https://brainly.com/question/30356348
#SPJ4
A circle has a circumference of 7{,}8507,8507, comma, 850 units. What is the radius of the circle?
Use 3. 14 for pi and enter your answer as a decimal
Answers
7,850 = 2 * 3.14 * r
Now, we'll solve for r:
7,850 = 6.28 * r
r = 7,850 / 6.28
r ≈ 1,250
So, the radius of the circle is approximately 1,250 units.
Why is math stu pid? It is no point? me think that. Also grammer
Answers
Answer:
I don't think there is a point to math lol
Answer:
it depends on what job you want
I think we should be able to choose what classes we take in high school but then Idek what i want to do sooo that's also a problem
A car depreciates in value by 17% per year.
If it cost $23 000 when it was new, how much is it worth after 4 years?
Answers
Answer:
17%of 23000
17/100×23000
1 yrs depreciation is 3910
then
after 4 years depreciation is 4×3910
=15640
the worth of after 4 yrs is 23000-15640
=Rs 7360
The mean mass of five men is 76 kg. The masses of four of the men are 72 kg, 74 kg, 75 kg and 81 kg. What is the mass of the fifth man
Answers
Answer:
78kg
Step-by-step explanation:
76×5= 380kg
380-72-74-75-81= 78kg
x=(76.5)-302
x=380-302=78
what's the area of 89 and 76
Answers
1.)Gcf of 89 and 76
\(gcf(89and76)\)
2)step 2
\( = \frac{89 \times 76}{lcm(89and76)} \)
3.)step 3
\( = \frac{6767}{6767} = 1\)
4.)answer
\(1\)
What is the length of Line segment S A? 1. 89 ft 2. 43 ft 3 ft 7 ft.
Answers
In the given figure, we can observe that two triangles are formed: ΔASB and ΔTSC.
It is given that:
Length of ST = 54 ft
Length of TB = 25 ft
Length of SC = 18 ft
To find: The length of SA
The length of TA can be found as follows:
Using the Pythagorean theorem,
In ΔTSC,TS² + SC² = TC²
54² + 18² = TC²
2916 + 324 = TC²
3240 = TC²
TC = 60 ft
Now, in ΔTSA,
TS² + SA² = TA²
60² + SA² = TA²
3600 + SA² = TA²
In ΔTAS,
TA² + AS² = TS²
TA² + AS² = 60²
TA² + AS² = 3600
In ΔASB,
AB² + BS² = AS²
AB² + 25² = AS²
AB² = AS² - 625
In ΔAST,
AS² + ST² = AT²
AS² + 54² = AT²
AS² + 2916 = AT²
From the above equations,
AS² - 625 + 2916 = AT²
AS² + 2291 = AT²
Substituting this value in ΔTAS:
TA² + AS² = 3600
TA² + (AT² - 2291) = 3600
TA² + AT² - 2291 = 36002
TA² = 5891TA² = 2945
TA = 54.23 ft (approx.)
Therefore, the length of SA is
From the above calculation, the length of SA is 43 ft.
In the given figure, two triangles are formed ΔASB and ΔTSC. We are to find the length of segment SA.
For that, we use the Pythagorean theorem to find the length of AT first.
The length of ST is 54 ft, SC is 18 ft and the length of TB is 25 ft. Applying the Pythagorean theorem, we get the length of TC as 60 ft.
Using this value, we apply the Pythagorean theorem again to find the length of AT, which comes out to be 54.23 ft (approx.).
Now that we have the length of AT, we apply the Pythagorean theorem in the triangle ΔTAS.
We find that the value of TA² is 2945. Substituting this value in the equation, we get that the length of SA is 43 ft.
Therefore, the length of line segment SA is 43 ft.
Therefore, from the above calculation, the length of line segment SA is 43 ft.
To know more about Pythagorean theorem, visit:
brainly.com/question/10368101
#SPJ11
Plot the following equation in the complex Cartesian plane: 2Re(z) m(z 2 ) −3≥ Im(iz)
Answers
The equation to plot in the complex Cartesian plane is 2Re(z) - |z²| ≥ -3Im(iz).
To plot the equation 2Re(z) - |z²| ≥ -3Im(iz) graphically, you can follow these steps:
1. Represent the complex number z in terms of its real and imaginary parts, z = x + yi, where x is the real part and y is the imaginary part.
2. Substitute the values of x and y into the equation and simplify it.
3. Separate the equation into real and imaginary parts.
4. For each part, plot the corresponding inequality on the Cartesian plane.
- For the real part, plot the inequality 2x - |(x + yi)²| ≥ -3y.
- For the imaginary part, plot the inequality 0 ≥ 0 (as -3Im(iz) = 0 for all values of x and y).
5. Determine the common region that satisfies both inequalities. This region represents the solution to the original equation.
Learn more about complex number
https://brainly.com/question/20566728
#SPJ11
A ladder is placed against a building so that it reaches 35 feet up the side of the building when its base is 12 feet from the base of the building. How long is the ladder?
Answers
Answer:
35 multiplied by 12
Step-by-step explanation:
Because either you multiply it or you do sohcahtoa
A coach records the ages of the players on two of her teams. Which statement about the ages of the students is true? A The range of ages is the same for both teams.The range of ages is the same for both teams. B The mode(s) of the ages is the same for both teams.The mode(s) of the ages is the same for both teams. C The mean age of the players on the volleyball team is less than the mean age of the players on the baseball team.The mean age of the players on the volleyball team is less than the mean age of the players on the baseball team. D The median age of the players on the volleyball team is greater than the median age of the players on the basketball team.
Answers
Answer:
Bro u need to put in the graph or the chart or something
Step-by-step explanation:
Help
Help
Help
Help. Help help help help help help help help

twice the difference of a number z and 12
Answers
The algebric expression "Twice the difference of a number z and 12" is equivalent to 2z - 24.
The phrase "Twice the difference of a number z and 12" represents a mathematical expression that can be written as 2(z - 12). Let's break down the meaning and interpretation of this expression.
First, we have the number z. This represents an unknown value or variable. It can be any real number.
Next, we have the difference of z and 12, which is obtained by subtracting 12 from z. So, z - 12 represents the numerical difference between z and 12.
Finally, we have "twice" this difference, which means multiplying the difference by 2. Therefore, we multiply z - 12 by 2, giving us the expression 2(z - 12).
To simplify this expression, we distribute the 2 to both terms inside the parentheses:
2(z - 12) = 2z - 24
The phrase represents an algebraic expression that calculates the result of doubling the difference between a given number z and 12. By substituting a specific value for z, you can evaluate the expression to obtain a numerical result.
For more such question on algebric expression. visit :
https://brainly.com/question/4344214
#SPJ8
How to solve for x also what is an equation that I could do?

Answers
Answer:
x=15
Step-by-step explanation:
5x+17+36=128
5x+53=128
5x=75
x=15
An explanation for the results is that those over the age of 55 grew up exposed to media that was displayed in black and white. Can these results be used to verify that explanation? A. No. The results speak to a possible difference between the proportions of people over 55 and under 25 who dream in black and white, but the results cannot be used to verify the cause of such a difference. B. Yes. The results can be used to verify the given explanation because the difference in proportions is statistically significant. C. Yes. The results can be used to verify the given explanation because the difference in proportions is practically significant. D. No. The results speak to a possible difference between the proportions of people over 55 and under 25 who dream in black and white, but the results are not statistically significant enough to verify the cause of such a difference.
Answers
Answer:
No. The results speak to a possible difference between the proportions of people over 55 and under 25 who dream in black and white, but the results cannot be used to verify the cause of such a difference.
Hence the correct option is option A.
A right triangle has side lengths 5, 12 and 13 as shown below use these lengths to find cosB tan B and sin B
PLZ SOMEONE HELP BRAINLIEST

Answers
Answer:
Step-by-step explanation:

Answer:
see explanation
Step-by-step explanation:
cosB = \(\frac{adjacent}{hypotenuse}\) = \(\frac{BC}{AB}\) = \(\frac{5}{13}\)
tanB = \(\frac{opposite}{adjacent}\) = \(\frac{AC}{BC}\) = \(\frac{12}{5}\)
sinB = \(\frac{opposite}{hypotenuse}\) = \(\frac{AC}{AB}\) = \(\frac{12}{13}\)
a poll showed that 53.6% of americans say they believe that some psychics can help solve murder cases. what is the probability of randomly selecting someone who does not believe that some psychics can help solve murder cases.
Answers
The probability of randomly selecting someone who does not believe that some psychics can help solve murder cases is 46.4%. Hence, the answer is 46.4%.
Given the poll showed that 53.6% of Americans say they believe that some psychics can help solve murder cases.
We are to find the probability of randomly selecting someone who does not believe that some psychics can help solve murder cases.
Let us consider the following events:
Let A be the event that someone believes that some psychics can help solve murder cases and B be the event that someone does not believe that some psychics can help solve murder cases.
Then A and B are complementary events, that is A∩B=∅ (i.e., the events cannot happen at the same time) and A∪B = S (the event space).
Thus we can write P(A) = 53.6% and P(B) = 100% - 53.6% = 46.4%.
Therefore, the probability of randomly selecting someone who does not believe that some psychics can help solve murder cases is 46.4%. Hence, the answer is 46.4%.
Know more about probability here:
https://brainly.com/question/251701
#SPJ11
Is this true or false? Pls help a dumb person out
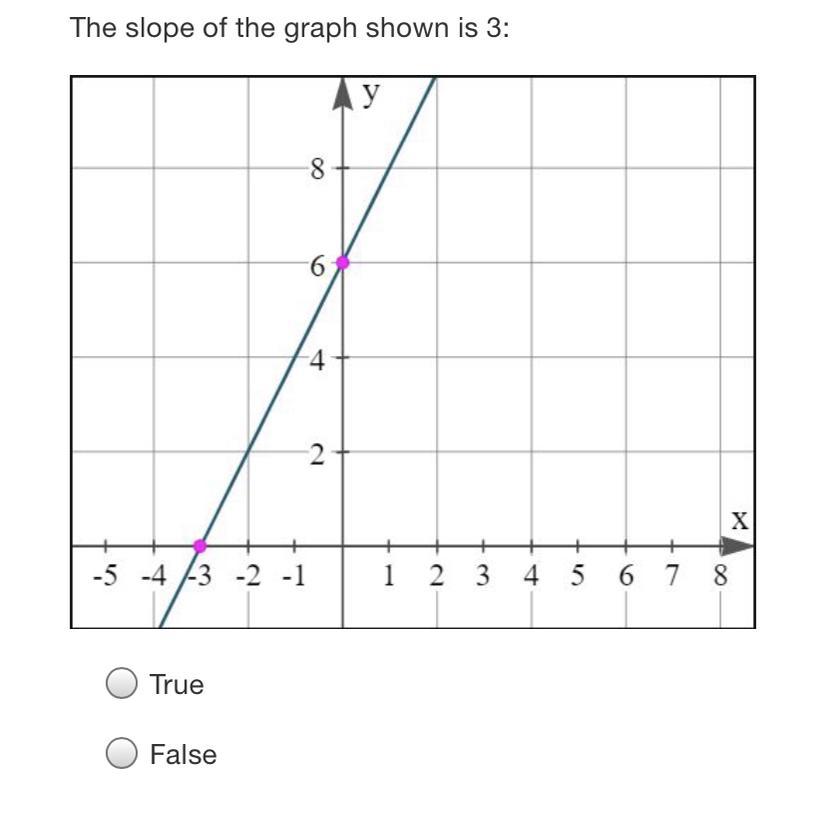
Answers
1. The campus demographics state that 40% of the students are male. If there are 300 students, how many are male?

Answers
Answer:
120 males
Step-by-step explanation:
Well you need to set up your proportions which should look like this x/300 and 40%/100%.You need to cross multiply meaning you need to multiply 300 and 40 which equals to 12,000 then you will divide 12,000 by 100 and get 120