an insurance provider claims that 80% of cars owners have no
accident in 2021. you randomly selected 6 car owners and asked
whether they had any accidents in 2021. 1. let X denote the number
of car ow
Answers
The probability of having exactly 4 car owners with no accidents in 2021 out of a random sample of 6 car owners is 0.2765.
We can solve this problem by using the binomial distribution formula since we are interested in the number of successes (car owners with no accidents) out of a fixed number of trials (the 6 randomly selected car owners).
The formula for the binomial distribution is P(X=k) = (n choose k) * p^k * (1-p)^(n-k), where n is the number of trials, k is the number of successes, p is the probability of success on any given trial, and (n choose k) is the binomial coefficient calculated as n!/((n-k)!*k!).
In this case, n=6, p=0.8 (the probability of a car owner having no accident), and we want to find P(X=4). Plugging these values into the formula, we get:
P(X=4) = (6 choose 4) * 0.8^4 * (1-0.8)^(6-4)
= 15 * 0.4096 * 0.04096
= 0.2765
Therefore, the probability of having exactly 4 car owners with no accidents in 2021 out of a random sample of 6 car owners is 0.2765.
It's worth noting that this calculation assumes that the insurance provider's claim of 80% is accurate and representative of the population as a whole. If the claim is not accurate or there are other factors that affect the likelihood of car accidents, then the results of this calculation may not accurately reflect the actual probability of having 4 car owners with no accidents in 2021.
Learn more about probability here
https://brainly.com/question/25839839
#SPJ11
Related Questions
Which angle measure is coterminal with the angle 7π/12? A) 15° (B) 125° (C) 285° (D) 465°
Answers
The angle measure that is coterminal with the angle 7π/12 is 285°. So, the correct option is C.
In trigonometry, coterminal angles are two angles in standard position with the same terminal side. It's not hard to notice that two angles are coterminal if one angle is a multiple of 360° added or subtracted from the other. For example, if an angle is -750°, it is coterminal with an angle of 30°.
To find coterminal angles with a given angle, add or subtract any multiple of 360 degrees (for degrees) or 2π (for radians). In this case, to find the coterminal angle for the angle 7π/12, you need to add or subtract 2π until you get an angle that's between 0 and 2π.7π/12 is equal to (2*π + 3π/12). As a result, it is a full circle with a remainder of 3π/12, or π/4.
The number of radians must be between 0 and 2π (360°) to find the coterminal angle. The number of radians to subtract or add is obtained by evaluating the number of full circles between the two angles.285° is equal to 5π/6 (in radians).
To determine the coterminal angle, add 2π to the angle (which is the equivalent of a full circle) so that the number of radians is between 0 and 2π.285° + 360° = 645°
In radians, 645° is equal to 11π/6, which is equivalent to 285°. Therefore, 285° is the angle measure that is coterminal with the angle 7π/12.
You can learn more about coterminal angles at: brainly.com/question/29133154
#SPJ11
what are some benefits of representing data sets using frequency distributions? what are some benefits of using graphs of frequency distributions?
Answers
The benefits of representing data sets with frequency distributions and
graphs helps us to have a clearer picture and understanding about the data.
The frequency distribution helps us to know which data is more
concentrated and the respective values for the subjects.
The representation also assists with finding the missing properties of the
data in question.
Read more on https://brainly.com/question/25269897
Determine the equation of the line in slope-intercept form (y = mx + b).

Answers
Answer:
y=3x-12
Step-by-step explanation:
to find slope we use y2-y1/x2-x1 by using any 2 points on the graph
(0,-12) (4,0)
0-(-12)/4-0)
12/4
3
The slope is 3
The y intercept is -12 since it crosses the y axis when y=-12
So we write those is y=Mx+b format where m is the slope and b is the y intercept
y=3x-12
Hopes this helps please mark brainliest
In a standard deck of cards what is the probability of choosing a red king replacing it and then choosing and then a club.
Answers
Answer:
1/104
Step-by-step explanation:
The probability of choosing a red king is 2/52 since there are only two red kings in a deck of 52 cards...the probability of choosing a club would be 13/52 since there are 13 club cardsin a deck of 52 cards
Therefore the probability of choosing both by replacing the king would be 2/52 × 13/52 giving us 1/104
Plz help fast will mark brainliest!!!

Answers
Answer:
well the answer is 0.185
Step-by-step explanation:
Point A has coordinates (−4,1), and point 8 has coordinates (0,13). What is the siope of a line segment connecting the two?
Answers
Answer:
3
Step-by-step explanation:
Slope m = (y2 - y1)/(x2 - x1)
m = (13 - 1)/(0 - -4) = 12/4 = 3
On a dogleg golf hole, one golfer hits the ball 250 yards and then another 150 yards to reach the green. The angle between the two hits is equal to 100 degrees. How far would the golfer have to originally hit the ball for it to go directly to the same position on the green
Answers
The distance the golfer has to originally hit the ball for it to go directly to the same position on the green is (B) d ≈ 313.087 yards.
What is the distance?Distance is a numerical measurement of the distance between two objects or points. The distance can refer to a physical length or an estimate based on other criteria in physics or everyday usage. The distance between two points A and B are sometimes denoted as |AB|.The given parameters are:
Distance traveled on first hit = 250 yardsDistance traveled on second hit = 150 yardsAngle between the two hits = 100°Required:
The distance the golfer is required to originally hit the ball to travel to the same location on the green.To calculate the distance between the two locations:
According to cosine law, we have:
d² = 250² + 150² - 2 × 250 × 150 × cos(100°)Where,
d = The distance between the initial and location on the greenIt gives,
d = √(250² + 150² - 250 × 150 × cos(100 Degrees)) ≈ 313.087The correct option is (B) 313.087 yards.Therefore, the distance the golfer has to originally hit the ball for it to go directly to the same position on the green is (B) d ≈ 313.087 yards.
Know more about distance here:
https://brainly.com/question/2854969
#SPJ4
The complete question is given below:
On a dogleg golf hole, one golfer hits the ball 250 yards and then another 150 yards to reach the green. The angle between the two hits is equal to 100 degrees. How far would the golfer have to originally hit the ball for it to go directly to the same position on the green?
(A) 98,023.613 yards
(B) 313.087 yards
(C) 142.570 yards
(D) 105.543 yards
Mai's teacher orders tickets to the local carnival for herself, the entire class, and 3 more chaperones. Student tickets are $4.50.
help me with the answer PLEASE
Answers
Answer: you take 4.50 multiply it by 4 for the chaperons and the teacher then multiply 4.50 by how many students there are then add those two together and there is your answer
Step-by-step explanation:
Which of the following fraction is the largest ?
5/6
7/12
4/7
2/3
Answers
Answer:
5/6
Step-by-step explanation:
So to do this, lets convert all of these fractions into decimals by dividing:
5/6 --> 0.833...
7/12 --> 0.583...
4/7 --> 0.571...
2/3 --> 0.66...
From this, it can be see that it is 5/6, since it is a larger decimal compared to the other choices.
Determine the 4th order Newton's divided-difference interpolating polynomial for the function below. Use x=1,4,5,6,8. Find the f(x) value at x=7 and x=9. f(x)=ln(x) clear; clc; close all; Hint: we already solved for a third order polynomial. Now you just heed to follow the pattern and create a 4th order. This means you will have 4 first divided differences, 3 second divided differences, 2 theird divided differences, and 1 fourth divided differences.
Answers
To find the 4th order Newton's divided-difference interpolating polynomial for f(x)=ln(x) with x=1,4,5,6,8, we first need to calculate the divided differences:
A. (a) The 4th order Newton's divided-difference interpolating polynomial for the function f(x) = ln(x) using the given data points is:
P(x) = ln(1) + (x - 1)[(ln(4) - ln(1))/(4 - 1)] + (x - 1)(x - 4)[(ln(5) - ln(4))/(5 - 4)(5 - 1)] + (x - 1)(x - 4)(x - 5)[(ln(6) - ln(5))/(6 - 5)(6 - 1)] + (x - 1)(x - 4)(x - 5)(x - 6)[(ln(8) - ln(6))/(8 - 6)(8 - 1)]
B. (a) To find f(x) at x = 7 and x = 9 using the interpolating polynomial, substitute the respective values into the polynomial expression P(x) obtained in the previous part.
Explanation:
A. (a) The 4th order Newton's divided-difference interpolating polynomial can be constructed using the divided-difference formula and the given data points. In this case, we have five data points: (1, ln(1)), (4, ln(4)), (5, ln(5)), (6, ln(6)), and (8, ln(8)). We apply the formula to calculate the polynomial.
B. (a) To find the value of f(x) at x = 7 and x = 9, we substitute these values into the polynomial P(x) obtained in the previous part. For x = 7, substitute 7 into P(x) and evaluate the expression. Similarly, for x = 9, substitute 9 into P(x) and evaluate the expression.
Learn more about polynomial
brainly.com/question/11536910
#SPJ11
Match the numbers with the correct label.

Answers
Answer:
a = \(\frac{1}{7}\)
b = .2
c= \(\frac{3}{9}\)
Step-by-step explanation:
You could change all of the numbers to decimals and then order
\(\frac{1}{7}\) ≈ .1428
.2 =.2
\(\frac{3}{9}\) ≈ .3
a random variable x follows a binomial distribution with mean 6 and variance 3.6. find the values of the parameters n and p
Answers
Values of parameters n and p for the binomial distribution with mean 6 and variance 3.6 are n=15 and p=0.4, respectively.
What is binomial?In probability theory and statistics, the binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent and identical trials, where each trial can result in only two possible outcomes, often labeled as "success" and "failure".
The distribution depends on two parameters: the probability of success (p) and the number of trials (n). The probability of getting exactly k successes in n trials can be calculated using the binomial probability mass function.
The binomial distribution has applications in various fields, including quality control, genetics, and finance, among others.
We know that for a binomial distribution, the mean and variance are given by:
Mean = np
Variance = np(1-p)
Substituting the given values, we have:
Mean = 6
Variance = 3.6
Thus, we can write two equations:
6 = np
3.6 = np(1-p)
We can solve for n and p by substituting the first equation into the second equation:
3.6 = (6/p) * (1-p) * p
3.6 = 6 - 6p
6p = 6 - 3.6
p = 0.4
Substituting this value of p into the first equation, we get:
6 = n * 0.4
n = 6 / 0.4
n = 15
Therefore, the values of the parameters n and p are n = 15 and p = 0.4, respectively.
To learn more about binomial click :
https://brainly.com/question/29163389
#SPJ1
what is the largest integer less than $2010$ that has a remainder of $5$ when divided by $7,$ a remainder of $10$ when divided by $11,$ and a remainder of $10$ when divided by $13$?
Answers
The largest integer less than 2010 that has a remainder of 5 when divided by 7, a remainder of 10 when divided by 11, and a remainder of 10 when divided by 13. is 1440
Given, a number less than 2010 that has a remainder of 5 when divided by 7, a remainder of 10 when divided by 11, and a remainder of 10 when divided by 13.
On using the Chinese remainder theorem. As, the numbers 7, 11, 13 are pairwise coprime.
Firstly, an integer m such that m−5 is divisible by 7 and m−10 is divisible by 11 .
The Chinese remainder theorem says that all integers that work will be of the form 54+7⋅11⋅k=54+77k for any integer k .
Next an integer n such that n−10 is divisible by 13 and n−54 is divisible by 77.
Then, by the Chinese remainder theorem, all the integers that also work are of the form 439+13⋅77⋅k=439+1001k .
Hence, the positive integers satisfying the condition are: 439, 439 + 1001 = 1440, 1440 + 1001 = 2441, and so on.
The largest integer less than 2010 is 1440.
Learn more about Chinese Remainder Theorem here https://brainly.com/question/10074520
#SPJ4
a woman whose mother is colorblind and whose father has hemophilia a is pregnant with a boy. what is the probability that her son will have normal vision and normal blood clotting? enter as a probability value between 0 and 1.
Answers
The required probability of the son with normal vision is 0.50 and for the normal blood clotting is 0.
If mutations is present on one of the X chromosome then it is capable of developing the condition which is called X-linked disorder.Generally men are affected by this disorder because they carry one copy of the X chromosome.If women carry one copy of the chromosome, then it is consider that they are carriers of disease and if they have both the copies affected then they are affected by disorder.Colorblind woman with a normal man is in position to produce 2 carrier females and 2 males colorblind.In the condition of a carrier woman with colorblindness marries a hemophilic man, progeny mentioned below phenotypes are produced:Parent phenotype Carrier woman
Affected man (Hemophilic) (colorblindness)
Parents X^h Y XX^C
Gametes X^h, Y X, X^C
Progeny X X^h X^C X^h X^C Y, XY
Total outcome = 100
Favourable outcomes for a son with normal vision is= 50
Probability of a son with normal vision = 50/100
= 0.50
probability of a son with normal blood clotting = 0 / 100
= 0
Therefore, the probability of the son with normal vision and normal blood clotting is 0.50 and 0 respectively.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
A recipe calls for 3 3/ 5 cups of kidney beans and 2 2/3 cups of diced tomatoes. if the recipe is multiplied by 2 1/2, how much of the mixture will there be?
Answers
Answer:
There will be 15 2/3 cups in the mixture.
Step-by-step explanation:
3 3/5 + 2 2/3 = 3 9/15 + 2 10/15 = 5 19/15
= 6 4/15
6 4/15 × 2 1/2 = 94/15 × 5/2 = 47/3 = 15 2/3
So there will be 15 2/3 cups in the mixture.
graph y=x+4
please help like rn

Answers
Answer:
y=4
Step-by-step explanation:
first you have y=mx+b
then b=4
and m=0
so it is
y=0x+4
or y=4
Animal Kingdom - You won the lottery and decided to buy all of the cats and dogs at a shelter and let them all roam free on a farm. You forgot to ask exactly how many dogs and how many cats they were giving you, but you know that there are 152 animals altogether and there are 3 times as many dogs as there are cats. Write an equation to find out the number of dogs and cats and then solve it.
Answers
Answer:
3x=152
Step-by-step explanation:
You know that there are 152 animals intotal so that goes at the end. if we say that the dogs are x because we dont know how many there are, then there are 3 times more cats then there are x.
Find the value of x…..

Answers
For the given parallel lines, the value of x is 22/3 or 7.3
Parallel lines
Parallel lines referred as the two lines in the same plane that are at equal distance from each other and never meet.
Given,
Here we have the parallel line with the angle (14x - 23)°, 16° and (8x + 21)°.
Now, we have to find the value of x.
While we looking into the give diagram, the given lines are parallel.
So, both of them have same angle.
So, we have to equate one with another to find the value of x,
=> 14x - 23 = 8x + 21
Here we need the value of x, so,
=> 14x - 8x = 21 + 23
=> 6x = 44
=> x = 44/6
=> x = 22/3 or 7.3
To know more about Parallel lines here.
https://brainly.com/question/16701300
#SPJ1
What is the half-life of a substance (in days) that decays to
35% its original amount in 6 days?
Answers
The half-life of the substance is approximately 14.4 days.
The half-life of a substance is the amount of time it takes for half of the substance to decay.
To find the half-life of a substance that decays to 35% its original amount in 6 days, we can use the following formula:
initial amount × (1/2)^(t/half-life) = final amount
We know that the final amount is 35% of the initial amount, or 0.35 times the initial amount. We also know that it takes 6 days for this decay to occur. So we can plug in these values and solve for the half-life:
initial amount × (1/2)^(6/half-life) = 0.35 × initial amount
Simplifying: (1/2)^(6/half-life) = 0.35
Dividing both sides by 1/2^(6/half-life):
1 = 0.35/(1/2)^(6/half-life)
Using the fact that (1/2)^(-x) = 2^x,
we can rewrite this as:
1 = 0.35 × 2^(6/half-life)
Taking the natural logarithm of both sides:
ln(1) = ln(0.35 × 2^(6/half-life))
ln(1) = ln(0.35) + ln(2^(6/half-life))
ln(1) = ln(0.35) + (6/half-life) × ln(2)
Simplifying: 0 = ln(0.35) + (6/half-life) × ln(2)
Solving for the half-life: ln(0.35) = -(6/half-life) × ln(2)
(1/half-life) = -ln(0.35) / (6 × ln(2))
half-life = -1 / [(6 × ln(2)) / ln(0.35)]
half-life ≈ 14.4 days
Therefore, the half-life of the substance is approximately 14.4 days.
Learn more about half-life visit:
brainly.com/question/31666695
#SPJ11
Which expression is equivalent to the given expression 2(3a+2b-7)
Answers
Step-by-step explanation:
2(3a+2b-7=6a+4b-146a+4b-146a=-4b+14a=(-4b+14)÷6a=(-4b+14)÷6 in 6a+4b-146({-4b+14}÷6)+4b-14
-4b+14+4b-14
0
a report summarized a survey of 2,305 working adults. the report indicates that 489 of the working adults surveyed said they were very concerned that their job will be automated, outsourced, or otherwise made obsolete in the next 5 years. the sample was selected in a way designed to produce a representative sample of working adults.
Answers
By using the concept of confidence interval, it can be concluded that-
Confidence interval = (0.1954, 0.2286)
We are 95 % confident that the true proportion of working adult who
were very concerned that their job will be automated, outsourced, or otherwise made obsolete in the next 5 years falls within this interval
Second option is correct
What is confidence interval?
Suppose there is a parameter which is unknown. Confidence interval will give the range of this unknown parameter.
Let the unknown parameter be θ, A confidence interval for the parameter θ is an interval (u, v)
where P(u < θ < v) = 1 - α, where P is the probability
α is called level of significance
Total number of working adults = 2305
Number of working adults surveyed = 489
Proportion of sample surveyed = \(\frac{289}{2305}=\) 0.212
Standard error = \(\sqrt{\frac{0.212 \times ( 1- 0.212)}{2305}} = 0.0085\)
At 95% confidence interval, z value = 1.96
Margin of error = 1.96 \(\times\) 0.0085 = 0.0166
Lower bound for the confidence interval = 0.212 - 0.0166 = 0.1954
Upper bound for the confidence interval = 0.212 + 0.0166 = 0.2286
Confidence interval = (0.1954, 0.2286)
Now since this is a problem on confidence interval, so a concept of confidence will come into question.
So, we are 95 % confident that the true proportion of working adult who
were very concerned that their job will be automated, outsourced, or otherwise made obsolete in the next 5 years falls within this interval
Second option is correct
To learn more about confidence interval, refer to the link-
https://brainly.com/question/15712887
#SPJ4
Complete Question
The complete question has been attached

Find the limit, if it exists, or show that the limit does not exist. lim(,)→(0,0) 2 2 4
Answers
The limit does not exist.
What is a limit?A limit in mathematics is the value that a function approaches when its input approaches some value. Limits are used to define continuity, derivatives, and integrals in calculus and mathematical analysis.In order for such a limit to occur, the fraction \(\frac{x^{2} }{x^{2} +y^{2} }\) must be comparable to the same value \(L\), regardless of the way we take to get there \((0,0)\).
Try approaching \((0,0)\) along the x-axis.
This means setting \(y=0\) and finding the limit \(lim_{x-0} \frac{x^{2} }{x^{2} +y^{2} }\).
We obtain:
\(lim_{x-0,y=0}\frac{x^{2} }{x^{2} +y^{2} } =lim_{y=0}}\frac{x^{2} }{x^{2} +0 }\\=lim_{x-0}} \frac{x^{2} }{x^{2} } \\\\=lim_{x-0}}1\\=1\)
Now evaluate approaching \((0,0)\) along the y-axis.
This means setting \(x=0\) and finding the limit \(lim_{y-0} \frac{x^{2} }{x^{2} +y^{2} }\).
\(lim_{y-0,x-0} \frac{x^{2} }{x^{2} +y^{2} } =lim_{y-0} \frac{0}{0+y^{2} } \\=lim_{y-0} \frac{0}{y^{2} } \\=lim_{y-0} 0\\=0\)
Approaching the origin via these two methods results in distinct limits.
\(lim_{x-0,y-0} \frac{x^{2} }{x^{2} +y^{2} }\) ≠ \(lim_{y-0,x-0}\frac{x^{2} }{x^{2} +y^{2} }\)
Therefore the limit does not exist.
Know more about limits here:
https://brainly.com/question/1521191
#SPJ4
The correct question is given below:
Find the limit, if it exists, or show that the limit does not exist.
\(lim_{(x,y) -(0,0)} \frac{x^{2} }{x^{2} +y^{2} }\)
What greater 50% or 13/25
Answers
Answer: 13/25
Step-by-step explanation: it is equal to 52% which is greater than 50%
50% is greater than 13/25. To compare these two values, you can convert both of them to a common denominator, such as 50%. 50% is equal to 1/2, so 13/25 is equal to 52/50, which is less than 1/2 or 50%. Alternatively, you can also express both fractions as decimals and compare the two values that way. 50% is equal to 0.5, and 13/25 is equal to 0.52, so 50% is still greater than 13/25.
Evaluate the expression below when x = 9 and y = 12.
4(x + 6) - 3(y + 4)
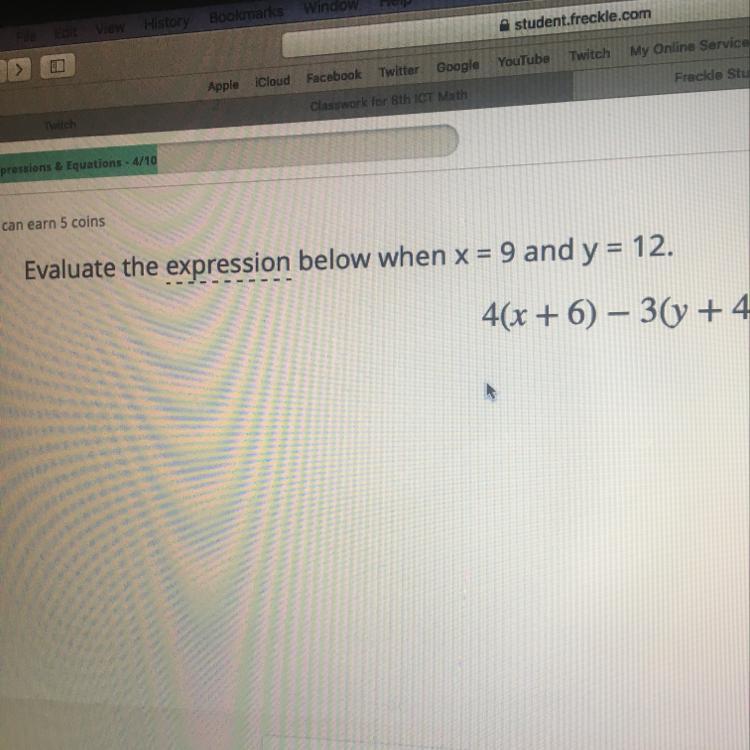
Answers
The scale of a map is 1: 250 000. On the map a large forest has an area of 6 cm2.
Calculate the actual area of the forest. Give your answer in square kilometres.
Answers
Answer:
37.5 km2 ...............
Determine the equation of the parabola graphed.
g(x)=
64
56
48
40
32
24
16
8
0
p
...
-2 -1
(-1, 4)
0
1
2
3 4
]
![Determine the equation of the parabola graphed.g(x)=6456484032241680p...-2 -1(-1, 4)0123 4]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/1dxnV7VwDedX5r2vWySWv4hfkL77nPQI.png)
Answers
The equation of the parabola is y = ( 4/3 ) ( x + 1 )² + 4
What is a Parabola?A Parabola, open curve, a conic section produced by the intersection of a right circular cone and a plane parallel to an element of the cone. A parabola is a plane curve generated by a point moving so that its distance from a fixed point is equal to its distance from a fixed line
The equation of the parabola is given by
( x - h )² = 4p ( y - k )
y = a ( x - h )² + k
where ( h , k ) is the vertex and ( h , k + p ) is the focus
y is the directrix and y = k – p
The equation of the parabola is also given by the equation
y = ax² + bx + c
where a , b , and c are the three coefficients and the parabola is uniquely identified
Given data ,
Let the equation of parabola be represented as A
Now , the value of A is
Let the vertex of the parabola be V
Now , the coordinates of P is V ( -1 , 4 )
and , equation of the parabola is given by
( x - h )² = 4p ( y - k )
y = a ( x - h )² + k
On simplifying , we get
y = a ( x - ( - 1 ) ) + 4
y = a ( x + 1 )² + 4
Now , the point on the parabola is given by P ( 2 , 16 )
On simplifying , we get
when x = 2 and y = 16
16 = a ( 2 + 1 )² + 4
16 = 9a + 4
12 = 9a
a = 4/3
So , the the value of a is 4/3
And , the equation is g ( x ) = ( 4/3 ) ( x + 1 )² + 4
Therefore , the value of g ( x ) is ( 4/3 ) ( x + 1 )² + 4
Hence , the equation of parabola is g ( x ) = ( 4/3 ) ( x + 1 )² + 4
To learn more about parabola click :
https://brainly.com/question/24042022
#SPJ9
Brianna works at the local grocery store she needs to stock 4 shells with 120 boxs of cereal. How many boxes can she put on each shelf
Answers
Answer:
30 boxes of cereal
Step-by-step explanation:
Divide 120 boxes equally among 4 shelves. 120/4 = 30
Kim and Anthony start a dog walking business. During their first week, they paid $10 to make their business cards. Kim walked a dog for 15 minutes.
Part A - Which integers represent the dollar amounts either spent or earned during their first week Kim and Anthony were in business? Fill in all that apply.
$5 -$5 $10 -$10 -$6
Answers
Answer:
-10$
Step-by-step explanation:
Kim and Anthony spent 10 dollars on business cards and it does not say how much Kim earned for the dog walk so the correct integer is -10$
Let {
a
n
}
be a sequence and L
a real number such that lim
n
→
[infinity]
a
n
=
L
. Prove that {
a
n
}
is bounded.
Answers
To prove that the sequence {an} is bounded, we can utilize the fact that the limit of the sequence exists. Since the limit of {an} as n approaches infinity is L, we can conclude that there exists some positive integer N such that for all n greater than or equal to N, the terms of the sequence are arbitrarily close to L.
1. By considering the terms up to index N-1, we can find a maximum value M that is greater than or equal to all those terms. By choosing the larger of M and L, we can establish an upper bound for all terms of the sequence.
2. Let's assume that the limit of {an} as n approaches infinity is L. This means that for any given positive epsilon, there exists a positive integer N such that for all n greater than or equal to N, the absolute value of (an - L) is less than epsilon. In other words, the terms of the sequence {an} become arbitrarily close to L as n becomes larger.
3. Now, let's consider the terms of the sequence up to index N-1. Since there are only finitely many terms before index N, we can find the maximum value among those terms, denoted as M. We know that M is greater than or equal to all the terms before index N.
4. To establish an upper bound for the entire sequence {an}, we consider two cases: (1) M is greater than or equal to L, and (2) M is less than L. In case (1), we choose M as the upper bound for the entire sequence {an}. Since M is greater than or equal to all terms before index N, and for all n greater than or equal to N, the terms become arbitrarily close to L, M serves as an upper bound for the entire sequence.
5. In case (2), we choose L as the upper bound for the entire sequence {an}. Since L is the limit of the sequence, and for all n greater than or equal to N, the terms become arbitrarily close to L, L serves as an upper bound for the entire sequence.
6. Therefore, we have shown that in both cases, the sequence {an} is bounded, with an upper bound of either M or L, depending on the situation.
Learn more about sequence here: brainly.com/question/29394831
#SPJ11
If You have this information about return of stock in 3
periods:
-12%, 20% and 25%.
calculate:
a. The arithmetic average.
b. The geometric average.
Answers
Answer:
✔ ∅ a. The arithmetic average.Step-by-step explanation:
If You have this information about return of stock in 3
periods:
-12%, 20% and 25%.
calculate:
✔ ∅ a. The arithmetic average.
✘ O b. The geometric average.