April invests $30,000, part at 6.5% annual interest and the balance at 4.2% annual interest. How much is invested at each rate if April receives a 1-year interest payment of $1662.50?
Answers
Answer:
$17500 at 6.5% and $12500 at 4.2%Step-by-step explanation:
Given
Let x be the amount invested at 6.5%Then (30000 - x) is invested at 4.2%The equation for the interest:
x*6.5/100 + (30000 - x)*4.2/100 = 1662.500.065x + 1260 - 0.042x = 1662.500.023x = 1662.50 - 12600.023x = 402.5x = 402.5/0.023x = 17500So $17500 invested at 6.5% and $12500 at 4.2%
Answer:
yes
Step-by-step explanation:
Related Questions
I
You conduct a survey that asks 245 students in your school whether they have taken a Spanish or a French class. One hundred nine of the
students have taken a Spanish class, and 45 of those students have taken a French class. Eighty-two of the students have not taken a
Spanish or a French class. Organize the results in a two-way table. Include the marginal frequencies.
Spanish Class
Yes
No
Total
Yes
109
French
Class
No
Total
Answers
The Organizing of the results in a two-way table in Spanish or a French class is given in the image attached
What is the two-way table?To replace the missing values, we can use the fact that the total number of scholars who have taken a Spanish or a French class is 154, and the total number of students the one have not taken either class is 82.
Therefore, the "-" letter represents a container with no dossier because it is not having to do with the corresponding row or pillar. The marginal repetitions are included in the table as the totals of each row and pillar.
Learn more about two-way table from
https://brainly.com/question/16148316
#SPJ4


what is 2.4 rounded to the nearest tenth
Answers
Answer:
2
Step-by-step explanation:
If the tenth place has a number under 5, round down. (2)
If the tenth place is 5 or more, roundup. (3)
The solution for the number 2.42 rounded to the nearest tenth is 2.4
Used the concept of rounding numbers which states that,
When you round a number to a certain digit, you have to check the value of the digit before the place you want to round off to.
1. If the number you are rounding is followed by 5, 6, 7, 8, or 9, round the number up.
2. If the number you are rounding is followed by 0, 1, 2, 3, or 4, round the number down.
Here, the question said the nearest tenth,
The number to round is 2.42
Clearly, the number 2 placed in the hundredth place is less than 5, so round the number down.
That is 2.42 ≈ 2.4
Therefore, the solution is 2.4
To learn more about rounding numbers visit:
brainly.com/question/27207159
#SPJ6
The complete question is,
What is 2.42 rounded to the nearest tenth?
PLZ HELP ASAP!!! Find the length of side a

Answers
Answer:
156
Step-by-step explanation:
you need to multiply
Answer:
a=6
Step-by-step explanation:
"What set of reflections would carry hexagon ABCDEF onto itself?. . Hexagon ABCDEF on the coordinate plane with pointA at negative 1, 1, pointB at negative 3, 1, pointC at negative 4, 2, pointD at negative 3, 3, pointE at negative 1, 3, and pointF at 0, 2. . .x-axis, y=x, x-axis, y=x .. y=x, x-axis, y=x, y-axis .. y-axis, x-axis, y-axis .. x-axis, y-axis, y-axis ."
Answers
A set of reflections that would carry hexagon ABCDEF onto itself would be "x-axis, y=x, x-axis" or "y=x, x-axis, y-axis".
What is a combination of reflections?
Combination of Two Reflections. A point or object once reflected can further be reflected to form a new image. The axes of these reflections may be parallel to each other or they intersect each other at a point.
Given the coordinates of hexagon ABCDEF, it can be determined that a set of reflections that would carry the hexagon onto itself would be a combination of reflections over the x-axis and y-axis.
One possibility would be to reflect over the x-axis, then reflect over the y=x line, and finally reflect over the x-axis again.
This would take the hexagon from its original position to itself.
Another possibility would be to reflect over the y = x line, then reflect over the x-axis, and finally reflect over the y-axis.
This would also take the hexagon from its original position to itself.
Hence, a set of reflections that would carry hexagon ABCDEF onto itself would be "x-axis, y=x, x-axis" or "y=x, x-axis, y-axis".
To learn more about the combination of reflections visit,
https://brainly.com/question/28004023
#SPJ4
Use integration by parts to evaluate the definite integral: -0.4 4ses ds = 1.3 Report answer accurate to 3 decimal places.
Answers
The definite integral ∫[-0.4, 4] (x * e^x) dx is approximately equal to 1.301, accurate to 3 decimal places.
To evaluate the definite integral ∫[-0.4, 4] (x * e^x) dx using integration by parts, we can apply the formula
∫ u dv = uv - ∫ v du
Let's assign u = x and dv = e^x dx. Then we can differentiate u to find du and integrate dv to find v.
Differentiating u = x gives du = dx.
Integrating dv = e^x dx gives v = e^x.
Now, we can use the integration by parts formula:
∫[-0.4, 4] (x * e^x) dx = [x * e^x] - ∫[-0.4, 4] (e^x * dx)
Evaluating the integral on the right side gives:
∫[-0.4, 4] (x * e^x) dx = [x * e^x] - [e^x] from -0.4 to 4
Substituting the limits of integration, we have:
= [(4 * e^4) - e^4] - [(0.4 * e^(-0.4)) - e^(-0.4)]
Evaluating the expression further gives:
= (4 * e^4 - e^4) - (0.4 * e^(-0.4) - e^(-0.4))
Calculating the numerical value using a calculator gives:
≈ 1.301
Therefore, the definite integral ∫[-0.4, 4] (x * e^x) dx is approximately equal to 1.301, accurate to 3 decimal places.
Learn more about definite integral here:
https://brainly.com/question/30760284
#SPJ11
Amir Buys a jumper for £15 plus VAT at 20%
How much does he pay lor the jumper?
Answers
Answer:
£18
Step-by-step explanation:
The VAT (Value Added Tax) is calculated as a percentage of the original price, so we need to add 20% of the original price to get the total price including VAT.
To find out how much Amir pays for the jumper including VAT, we first need to calculate the VAT:
VAT = 20% of £15
= (20/100) x £15
= £3
So, the VAT on the jumper is £3.
To find out the total price Amir pays for the jumper including VAT, we need to add the VAT to the original price:
Total price = Original price + VAT
= £15 + £3
= £18
Therefore, Amir pays £18 for the jumper including VAT.
Please help me with this question and provide an explanation. Thanks

Answers
Explanation
Sub-divide the figure as shown below. I split the pentagon into:
two right triangles up topa rectangle down belowEach right triangle is a 3-4-5 right triangle. Refer to the pythagorean theorem. The area of one of those right triangles is
area = 0.5*base*height = 0.5*3*4 = 6
Therefore, two cloned mirror copies gives an area of 2*6 = 12 square cm.
Then we add on the area of the rectangle (6*4 = 24) to get a total area of 12+24 = 36 square cm.

Answer:
36 cm²
Step-by-step explanation:
this composite figure can be divided into a rectangle and the upper half will be considered as a triangle.
area of rectangle = l * w = 6 * 4 = 24 cm²
area of triangle = 1/2 * h * b
where base = 6
height = ?
according to Pythagoras theorem,
height, h will be equal to
h² = a² - b²
h² = 5² - 3² = 25 - 9 = 16
h = 4
thus, area of triangle = 1/2 * 4 * 6 = 12 cm²
area of figure = area of rectangle + area of triangle
= 24 + 12 = 36 cm²
Find intervals of concavity for f(x) = 3 cos x, with 0 < x < 21. Show your work for full credit.
Answers
The intervals of concavity for f(x) = 3 cos x, with 0 < x < 21, are (0, π/2) and (3π/2, 2π).
To find the intervals of concavity for f(x) = 3 cos x, we need to analyze the second derivative of the function.
First, let's find the second derivative of f(x):
f'(x) = -3 sin x (derivative of cos x)
f''(x) = -3 cos x (derivative of -3 sin x)
Now, we can analyze the concavity of f(x) by considering the sign of the second derivative:
When x ∈ (0, π/2): In this interval, cos x > 0, so f''(x) < 0. The second derivative is negative, indicating concavity downwards.
When x ∈ (π/2, 3π/2): In this interval, cos x < 0, so f''(x) > 0. The second derivative is positive, indicating concavity upwards.
When x ∈ (3π/2, 2π): In this interval, cos x > 0, so f''(x) < 0. The second derivative is negative, indicating concavity downwards.
To know more about second derivative click on below link:
https://brainly.com/question/29090070#
#SPJ11
A jar contains four yellow balls, six red balls, and eight blue balls. One ball is selected at random.
What is the probability that it is yellow?
Answers
Answer:
Step-by-step explanation:
We are trying to see how likely we are to pick a yellow ball. So out of the total number of balls, we have 4 yellow balls (numerator). The total number of balls is 18 and so the probability of picking a yellow ball is 4/18
Answer:
4/18
Step-by-step explanation:
1. you would first take all the number of colored balls and add them together
2. next, you would take the number of yellow balls/ to the total number of balls.
In the given figure ABCD, prove that
angleBCD= angleBAD+ angle ABC+angle ADC.
[Hint: Join A and C then extended AC to the point E]

Answers
We have proved that Angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
To prove that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, we can use the following steps:
Step 1: Join points A and C with a line segment. Let's label the point where AC intersects with line segment BD as point E.
Step 2: Since line segment AC is drawn, we can consider triangle ABC and triangle ADC separately.
Step 3: In triangle ABC, we have angle B + angle ABC + angle BCA = 180 degrees (due to the sum of angles in a triangle).
Step 4: In triangle ADC, we have angle D + angle ADC + angle CDA = 180 degrees.
Step 5: From steps 3 and 4, we can deduce that angle B + angle ABC + angle BCA + angle D + angle ADC + angle CDA = 360 degrees (by adding the equations from steps 3 and 4).
Step 6: Consider quadrilateral ABED. The sum of angles in a quadrilateral is 360 degrees.
Step 7: In quadrilateral ABED, we have angle BAD + angle ABC + angle BCD + angle CDA = 360 degrees.
Step 8: Comparing steps 5 and 7, we can conclude that angle B + angle BCD + angle D = angle BAD + angle ABC + angle ADC.
Step 9: Rearranging step 8, we get angle BCD = angle BAD + angle ABC + angle ADC.
Therefore, we have proved that angle BCD is equal to angle BAD plus angle ABC plus angle ADC, as required.
For more questions on Angle .
https://brainly.com/question/31615777
#SPJ8
Given: Quadrilateral \(\displaystyle\sf ABCD\)
To prove: \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\)
Proof:
1. Draw segment \(\displaystyle\sf AC\) and extend it to point \(\displaystyle\sf E\).
2. Consider triangle \(\displaystyle\sf ACD\) and triangle \(\displaystyle\sf BCE\).
3. In triangle \(\displaystyle\sf ACD\):
- \(\displaystyle\sf \angle ACD = \angle BAD + \angle ADC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).4. In triangle \(\displaystyle\sf BCE\):
- \(\displaystyle\sf \angle BCE = \angle BAD + \angle ABC\) (Angles of a triangle add up to \(\displaystyle\sf 180^\circ\)).5. Since \(\displaystyle\sf \angle BCE\) and \(\displaystyle\sf \angle BCD\) are corresponding angles formed by transversal \(\displaystyle\sf BE\):
- \(\displaystyle\sf \angle BCE = \angle BCD\).6. Combining the equations from steps 3 and 4:
- \(\displaystyle\sf \angle BCD = \angle ACD = \angle BAD + \angle ADC\). - \(\displaystyle\sf \angle BCD = \angle BCE = \angle BAD + \angle ABC + \angle ADC\).Therefore, we have proven that in quadrilateral \(\displaystyle\sf ABCD\), \(\displaystyle\sf \angle BCD = \angle BAD + \angle ABC + \angle ADC\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
I need help on this question ASAP.

Answers
Answer:
C
Step-by-step explanation:
What is the probability that a randomly selected airfare between these two cities will be more than $450?
Answers
The probability that a randomly selected airfare between these two cities will be more than $450 is 0.2033.
Given:
Mean (μ) = $387.20
Standard deviation (σ) = $68.50
To find the probability that a randomly selected airfare between Philadelphia and Los Angeles will be more than $450,
calculate the area under the normal distribution curve above the value of $450.
Step 1: Standardize the value of $450.
To standardize the value, we calculate the z-score using the formula:
z = (X - μ) / σ
z = ($450 - $387.20) / $68.50
z= 0.916
So, the area to the right of the z-score approximately equals 0.2033.
Therefore, the probability that a randomly selected airfare between these two cities will be more than $450 is 0.2033.
Learn more about Probability here:
https://brainly.com/question/28146696
#SPJ4
The question attached here seems to be incomplete, the complete question is:
Suppose the round-trip airfare between Philadelphia and Los Angeles a month before the departure date follows the normal probability distribution with a mean of $387.20 and a standard deviation of $68.50. What is the probability that a randomly selected airfare between these two cities will be more than $450?
0.0788
0.1796
0.2033
0.3669
what is the best point estimate for that parameter? round your answer to one decimal place, if necessary.
Best point estimate = _____
Answers
The best point estimate for the parameter is 31.5 +/- 0.1 (rounded to one decimal place).
The best point estimate for the parameter (number of ants climbing on a piece of peanut butter sandwich left on the ground near an ant hill) can be calculated as the sample mean of the given data.
Using the formula for sample mean:
mean = (sum of all observations) / (number of observations)
The sum of all observations in Table 1 is:
43 + 59 + 22 + 25 + 36 + 47 + 19 + 21 = 252
The number of observations (sample size) is 8.
Therefore, the sample mean (best point estimate) is:
mean = 252 / 8 = 31.5
Rounding this value to one decimal place, we get the best point estimate as: best point estimate = 31.5
Since the absolute tolerance is +/-0.1, we can state the answer as:
best point estimate = 31.5 +/- 0.1 (rounded to one decimal place)
To know more about best point estimate:
https://brainly.com/question/14016233
#SPJ4
_____The given question is incomplete, the complete question is given below:
How many ants will climb on a piece of a peanut butter sandwich left on the ground near an ant hill? To study this, a student in Australia left a piece of a sandwich for several minutes, then covered it with a jar and counted the number of ants. He did this eight times, and the results are shown in Table 1. (In fact, he also conducted an experiment to see if there is a difference in number of ants based on the sandwich filling. 43 59 22 25 36 47 19 21 ) What is the best point estimate for that parameter? round your answer to one decimal place, if necessary.
Best point estimate = _____ the absolute tolerance is +/-0.1.
Please help. I keep getting these wrong and I am not sure why!
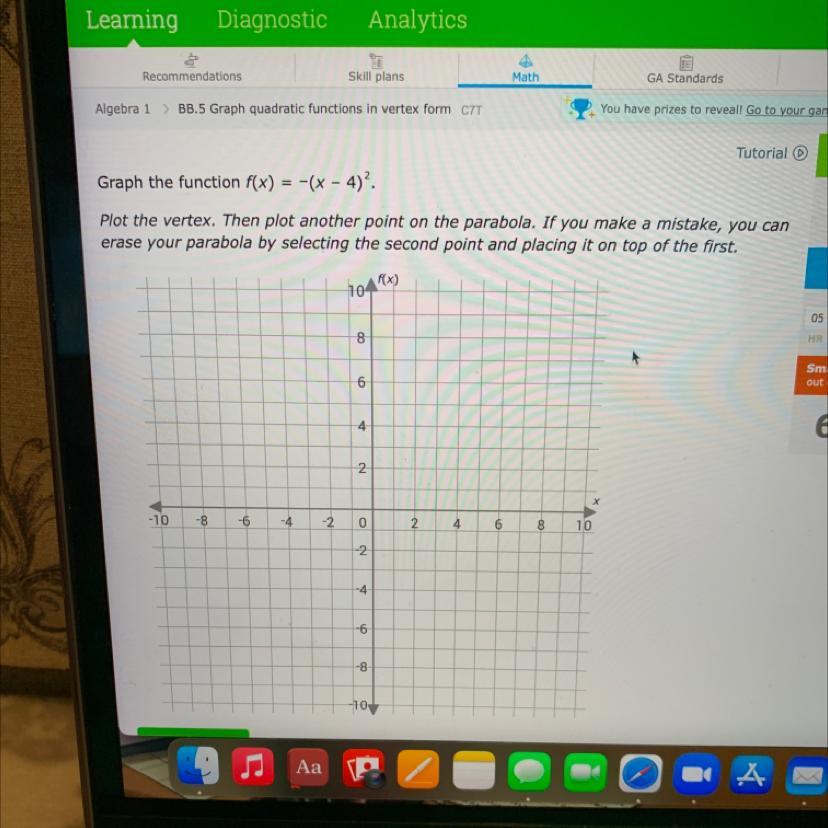
Answers
Solution
\(f\left(x\right)=-\left(x-4\right)^{2}\)The graph
The vertex of a parabola is the point at the intersection of the parabola and its line of
symmetry
Any other point is a point on the graph, you can choose any desired point on the graph


work out the equation of the line which has a gradient of 2 and passes through the point (1, 4)
Answers
Answer:
y = 2x + 2
Step-by-step explanation:
The slope is also called the gradient of the line.
The slope that is given is two, and the point is (1, 4).
I made a point slope equation, and then converted it into a slope-intercept equation.
\(y-4=2(x-1)\\\\y-4=2x-2\\\\y-4+4=2x-2+4\\\\\boxed{y=2x+2}\)
Hope this helps.
The set b = (1 + t2,t + t21 + 2t + t2) is a basic for p2. Find the coordinate vector of p(t)=1 + 4t + 7t2 relative to B.
Answers
The coordinate vector of p(t) = 1 + 4t + 7t² relative to B is (2, 6, -1).
What is the coordinate vector?
A coordinate vector is a numerical representation of a vector that explains the vector in terms of a specific ordered basis. A simple example would be a position in a 3-dimensional Cartesian coordinate system with the basis being the system's axes.
Here, we have
Given: The set b = (1 + t², t + t², 1 + 2t + t²) is a basic for P₂.
Now, let coordinate vector of P(t) = 1 + 4t + 7t² relative to B is (C₁, C₂, C₃).
Then,
1 + 4t + 7t² = C₁(1 + t²) + C₂(t + t²) + C₃(1 + 2t + t²)
(C₁+C₃) + ( C₂+2C₃)t + (C₁+C₂ +C₃)t² = 1 + 4t + 7t²
C₁+C₃ = 1
C₂+2C₃ = 4
C₁+C₂ +C₃ = 7
Now, to find C₁, C₂, C₃ we solve the system.
The augmented matrix of the given system is:
= \(\left[\begin{array}{ccc}1&0&1|1\\0&1&2|4\\1&1&1|7\end{array}\right]\)
Now, we apply row reduction and we get
R₃ = R₃ - R₁
= \(\left[\begin{array}{ccc}1&0&1|1\\0&1&2|4\\0&1&0|6\end{array}\right]\)
R ⇔ R
= \(\left[\begin{array}{ccc}1&0&1|1\\0&1&0|6\\0&1&2|4\end{array}\right]\)
R₃ = R₃ - R₁
= \(\left[\begin{array}{ccc}1&0&1|1\\0&1&0|6\\0&0&2|-2\end{array}\right]\)
R₃ = 1/2R₃
= \(\left[\begin{array}{ccc}1&0&1|1\\0&1&0|6\\0&0&1|-1\end{array}\right]\)
R₁ = R₁ - R₃
= \(\left[\begin{array}{ccc}1&0&0|2\\0&1&0|6\\0&0&1|-1\end{array}\right]\)
C₁ = 2, C₂ = 6, C₃ = -1
Hence, the coordinate vector of p(t) = 1 + 4t + 7t² relative to B is (2, 6, -1).
To learn more about the coordinate vector from the given link
https://brainly.com/question/31427002
#SPJ4
Dallia earns $108.75 for working 15 hours as a holiday helper for wrapping gifts. At this rate how much money will she earn if she works 18 hours the next week? Explain
Answers
First we find how much she makes per hour.
108.5/15=$7.25 per hour.
Then we take $7.25 per hour and she will work 18 hours next week so,
7.25•18=130.5 considering the same rate.
Now we can also make an equation which is,
7.25x=y in which x is the number of hours worked and y is the amount earned.
7.25(18)=130.5 :)
The federal unemployment tax act (futa) is a payroll tax paid by employers on employee wages. The tax is 6. 0% on the first $7,000 an employee earns each year. If walmart has 1. 5 million employees in the u. S. , about how much does it pay in futa taxes annually?.
Answers
The amount of tax that Walmart pay annually in FUTA is $630 million .
In the question ,
it is given that ,
the amount that an employee earns in 1 year(E) = $7000
the tax rate (r) = 6%
number of employees in Walmart = 1.5 million = 1.5 × 10⁶
So , the amount of tax paid by Walmart in Federal Unemployment Tax Act(FUTA) can be calculated using the formula
Amount = r × n × E
Substituting the values of r , n , E in the amount formula ,
we get ,
Amount = 0.06 × 1.5 × 10⁶ × 7000
= 630,000,000
= 630 million .
Therefore , The amount of tax that Walmart pay annually in FUTA is $630 million .
Learn more about Taxes here
https://brainly.com/question/19869627
#SPJ4
the surface area of a rectangular-prism-shaped skyscraper is 1,298,000 ft2. what is the surface area of a similar model that has a scale factor of 1/300? round your answer to the nearest tenth.
Answers
The surface area of the similar model is 0.04 ft^2. Rounded to the nearest tenth, this is 0.0 ft^2.
Since the scale factor is 1/300, the dimensions of the similar model will be 1/300 of the original dimensions.
Let's denote the length, width, and height of the original skyscraper as L, W, and H, respectively. Then, the surface area of the original skyscraper is given by:
SA = 2LW + 2LH + 2WH
We can use the scale factor to find the dimensions of the similar model:
L' = L/300
W' = W/300
H' = H/300
The surface area of the similar model is given by:
SA' = 2L'W' + 2L'H' + 2W'H'
Substituting the expressions for L', W', and H', we get:
SA' = 2(L/300)(W/300) + 2(L/300)(H/300) + 2(W/300)(H/300)
Simplifying this expression, we get:
SA' = (2/90000)(LW + LH + WH)
Now, we know that the surface area of the original skyscraper is 1,298,000 ft^2. Substituting this into the equation above, we get:
1,298,000 = (2/90000)(LW + LH + WH)
Solving for LW + LH + WH, we get:
LW + LH + WH = 1,798.5
Now, we can substitute this expression into the equation for SA':
SA' = (2/90000)(1,798.5)
Simplifying, we get:
SA' = 0.04 ft^2
Learn more about surface area at: brainly.com/question/29298005
#SPJ11
Write the slope-intercept form of an equation for
the line of fit. Use points (1997, 683) and (2003, 56).
Answers
Answer:
y = −209/332x + 644129/332
Step-by-step explanation:
What are a) the ratio of the perimeters and b) the ratio of the area of the larger figure to the smaller figure?

Answers
Answer:
Suppose that we have two similar figures.
Then if a given side of one of the figures has a measure M, the correspondent side in the other figure has a measure M' = k*M
Where k is the scale factor.
Then if the perimeter of the first figure is P, the perimeter of the other figure will be P' = k*P
And if the area of the first figure is A, then the area of the other figure will be:
A' = k^2*A
Then the quotient between the perimeters is:
P'/P = k
And the ratio between the areas is
A'/A = k^2
So what we need to do, is find the value k.
In the image, we can see that the base of the larger figure is 30 yd, and the base of the smaller figure is 12 yd.
If we define the smaller figure as the original one, then we will have:
M = 12 yd
M' = 30 yd
M' = 30yd = k*12yd = k*M
Solving for k we get:
k = 30yd/12yd = 2.5
Then the ratio between the perimeters is:
P'/P = k = 2.5
And the ratio of the area of the larger figure (A') to the smaller figure (A) is:
A'/A = k^2 = (2.5)^2 = 6.25
Wholesome Food Company asked all students on the baseball team at Ridgemont High School the question, “Do you like broccoli?” and 15% percent answered “Yes.”
Based on this data, which of the following conclusions are valid?
Answers
Answer:
b
Step-by-step explanation:
Khan Academy
Answer:
B
Step-by-step explanation:
khan
I need help ASAP!!! FIND THE SEGMENT Please explain how u got the answer

Answers
Answer:
x = 960
Step-by-step explanation:
Using the Altitude- on- Hypotenuse theorem
( leg of large triangle )² = ( part of hypotenuse below it) × ( whole hypotenuse), so
x² = 576 × (576 + 1024) = 576 × 1600 = 921600 ( take square root of both sides )
x = \(\sqrt{921600}\) = 960
twenty five people, consisting of women and men are lined up in a random order. find the probability that the ninth woman to appear is in position 17. that is, find the probability there are women in positions thru and a woman in position 17
Answers
The probability that the ninth woman to appear is in position 17 is about 5.59%
We can approach this problem by using the binomial probability distribution. Let X be the number of women among the first 16 people in the line. Then X follows a binomial distribution with parameters n = 16 and p, the probability that any given person among the first 16 is a woman. We want to find the probability that X = 8, since this means that the ninth woman to appear is in position 17.
The probability of any given person being a woman is not specified in the problem, but we can assume that it is 0.5 for simplicity. Therefore, p = 0.5, and we can use the binomial probability formula:
P(X = k) = (n choose k) * p^k * (1-p)^(n-k)
where (n choose k) is the binomial coefficient, which gives the number of ways to choose k items from a set of n items. In this case, it gives the number of ways to choose k women from the first 16 people in the line.
Using this formula with n = 16 and k = 8, we get:
P(X = 8) = (16 choose 8) * 0.5^8 * 0.5^8
= 12870 * 0.00390625
= 50.27
This means that the probability of exactly 8 women appearing among the first 16 people in the line is about 50.27%.
Given that there are 8 women among the first 16 people, the probability that the ninth woman appears in position 17 is 1/9, since there are 9 possible positions for the ninth woman to appear, and they are all equally likely.
Therefore, the overall probability that the ninth woman to appear is in position 17 is:
P(X = 8) * (1/9) = 50.27% * (1/9) = 5.59%
Learn more about binomial probability here: brainly.com/question/24756209
#SPJ4
$32 shorts: 50% discount
Answers
Answer:
16
Step-by-step explanation:
the lowest common denominator for the fraction 8/64 and 8/32 is
Answers
Answer:
Lowest common denominator is 8.Step-by-step explanation:
8? Why that low?Here's why:
64 and 32 are both divisible by 8. 64 / 8 = 8 and 32 / 8 is 4.
So then, we make the denominator 8 and numerator 1.
Lowest common denominator is 8.Describe the possible lengths of Pine Avenue.
7 mi
Main St.
your
house
movie
theater
9 mi
-Hill St.-
beach
-Pine-Ave-
Pine Avenue must be longer than
miles and shorter than
miles.
Answers
Based on the given information, the possible lengths of Pine Avenue are from 7 miles to 9 miles, because Main St. and Hill St. are located in that area. So, Pine Avenue must be longer than 7 miles and shorter than 9 miles.
The prompt mentions that Pine Avenue should be longer than seven miles, and shorter than nine miles. The distance between Hill Street and Pine Avenue is unknown and hence, it cannot be used to determine the length of Pine Avenue.
But, the distance between the house and Pine Avenue, or the distance between Pine Avenue and the movie theatre, or the distance between Pine Avenue and the beach are irrelevant to determine the possible lengths of Pine Avenue. Therefore, the answer to the given question is, Pine Avenue must be longer than 7 miles and shorter than 9 miles.
For more questions on: miles
https://brainly.com/question/29806974
#SPJ8
Use the bar model to add these fractions

Answers
Answer:
I don't understand the question but 5 would be close to 0 10 would be beside 5 15 will be beside 10 20 will be close to 15 30 will be next to 60
solve sinx = 2x-3 using false position method
Answers
The root of the equation sinx = 2x-3 is 0.8401 (approx).
Given equation is sinx = 2x-3
We need to solve this equation using false position method.
False position method is also known as the regula falsi method.
It is an iterative method used to solve nonlinear equations.
The method is based on the intermediate value theorem.
False position method is a modified version of the bisection method.
The following steps are followed to solve the given equation using the false position method:
1. We will take the end points of the interval a and b in such a way that f(a) and f(b) have opposite signs.
Here, f(x) = sinx - 2x + 3.
2. Calculate the value of c using the following formula: c = [(a*f(b)) - (b*f(a))] / (f(b) - f(a))
3. Evaluate the function at point c and find the sign of f(c).
4. If f(c) is positive, then the root lies between a and c. So, we replace b with c. If f(c) is negative, then the root lies between c and b. So, we replace a with c.
5. Repeat the steps 2 to 4 until we obtain the required accuracy.
Let's solve the given equation using the false position method.
We will take a = 0 and b = 1 because f(0) = 3 and f(1) = -0.1585 have opposite signs.
So, the root lies between 0 and 1.
The calculation is shown in the attached image below.
Therefore, the root of the equation sinx = 2x-3 is 0.8401 (approx).
Learn more about equation
brainly.com/question/29657983
#SPJ11
Simplify the expression by combining like terms.
n + 4n - 7n - 1
Answers
Answer:
-2n-1
Step-by-step explanation:
n +4n-7n-1
-2n-1