Answers
Answer:
D is correct.
Step-by-step explanation:
\(3 |x + 1| < 6\)
\( |x + 1| < 2\)
\( - 2 < x + 1 < 2\)
\( - 3 < x < 1\)
x > 3 and x < 1, so D is correct.
Related Questions
Shandra i working two ummer job, making $9 per hour wahing car and $8 per hour walking dog. Lat week Shandra worked a total of 11 hour and earned a total of $90. Write a ytem of equation that could be ued to determine the number of hour Shandra worked wahing car lat week and the number of hour he worked walking dog lat week. Define the variable that you ue to write the ytem
Answers
The system of equations that could be used to determine the number of hours Shandra worked washing cars last week and the number of hours she worked walking dog last week is :
9x + 8y = 90
x + y = 11
What exactly is an expression?
When using operations like addition, subtraction, multiplication, and division, a mathematical expression are defined as a collection of numbers, variables, and functions.
Given,
Shandra makes $9 per hour washing cars.
Shandra makes $8 per hour by walking dogs.
Total no. of hours she worked last week = 11
Total money she earned last week = $90
Let the no. of hours she washes cars = x
Let the no. of hours she walks dogs = y
Therefore,
9x + 8y = 90
x + y = 11
Hence, these two are the expression .
To learn more about system of equations here:
https://brainly.com/question/12895249
#SPJ4
why is crout factorization faster than gaussian
Answers
Crout factorization is faster than Gaussian elimination because it takes advantage of the structure of a matrix and reduces the number of operations required to solve a system of linear equations.
In Crout factorization, the matrix is decomposed into a lower triangular matrix and an upper triangular matrix, which can be solved efficiently using forward and backward substitution.
This technique avoids the need for row interchanges, which are required in Gaussian elimination to avoid dividing by zero and to choose the largest pivot element. Row interchanges are computationally expensive because they require swapping entire rows of the matrix.
Additionally, Crout factorization is more numerically stable than Gaussian elimination because it produces a factorization that is less sensitive to rounding errors in the coefficients of the system of linear equations.
To know more about Gaussian elimination refer here:
https://brainly.com/question/31328117
#SPJ11
A person sitting in the top row of the bleachers at a sporting event drops a pair of sunglasses from a height of 24 feet. The function h=-16x^2+24 represents the height (h) (in feet) of the sunglasses after x seconds. How long does it take the sunglasses to hit the ground, rounded to the nearest tenth?
Answers
1.2 seconds it take the sunglasses to hit the ground
To find how long it takes for the sunglasses to hit the ground, we need to find the value of x when h = 0.
We can set the function equal to 0 and solve for x:
-16x² + 24 = 0
Dividing both sides by -16 gives:
x² - (24/-16) = 0
x² - 1.5 = 0
x² = 1.5
x = ±√1.5
x = √1.5 seconds for the sunglasses to hit the ground.
we get x = 1.2 seconds.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
The volume of a right rectangular prism can be found by finding the product 3(6)(12) Which expression could also be used to determine the volume of this prism? 36(6) 2(3 + 12 + 6) 4(3)(12) 12 + 6 +3
Answers
Answer:
D
Step-by-step explanation:
Find f such that f'(x) = 8x - 7. f(5) = 0. Enter your answer in the answer box.
Answers
The function f(x) that satisfies f'(x) = 8x - 7 and f(5) = 0 is:
\(f(x) = 4x^2 - 7x - 65\)
How to find f such that f'(x) = 8x - 7. f(5) = 0?To find the function f, we need to integrate f'(x) = 8x - 7 with respect to x.
∫f'(x) dx = ∫(8x - 7) dx
\(f(x) = 4x^2 - 7x + C\), where C is a constant of integration.
To find the value of C, we use the fact that f(5) = 0.
\(0 = 4(5)^2 - 7(5) + C\)
0 = 100 - 35 + C
C = -65
Therefore, the function f(x) that satisfies f'(x) = 8x - 7 and f(5) = 0 is:
\(f(x) = 4x^2 - 7x - 65\)
Learn more about Finding a Function Given Its Derivative and a Point on the Curve
brainly.com/question/29148660
#SPJ11
Need the answer to this please

Answers
T/F : the pearson’s linear correlation coefficient measures the association between two continuous random variables. if its value is near ±1, the association is quasi perfectly linear.
Answers
True. The Pearson's linear correlation coefficient is a measure of the strength and direction of the linear relationship between two continuous random variables.
It ranges from -1 to 1, with values closer to -1 or 1 indicating a stronger linear correlation. If the value is near ±1, then the association between the variables is quasi perfectly linear. However, it is important to note that correlation does not imply causation and that other types of relationships between variables may exist beyond linear associations. In conclusion, the Pearson's linear correlation coefficient is a useful tool for assessing the strength and direction of linear relationships between continuous variables.
To know more about correlation visit:
https://brainly.com/question/30116167
#SPJ11
Answer for ten points!
Answers
Answer:
Step-by-step explanation:
An Amtrak official obtains data on a particular day concerning the length of time (in minutes) that the metroliners leaving New York take to reach Philadelphia, with the following results:
93 89 91 87 91 89
Find the sample variance.
a. 3.6
b. 5.6
c. 6.8
d. 7.6
e. 4.4
Answers
The sample variance for the given data is 4.4 minutes. This corresponds to option e. in the list of choices provided.
The sample variance is a measure of how much the individual data points in a sample vary from the mean.
It is calculated by finding the average of the squared differences between each data point and the mean.
To find the sample variance for the given data on the length of time taken by metroliners to reach Philadelphia, we follow these steps:
Calculate the mean (average) of the data set:
Mean = (93 + 89 + 91 + 87 + 91 + 89) / 6 = 540 / 6 = 90
Subtract the mean from each data point and square the result:
(93 - 90)^2 = 9
(89 - 90)^2 = 1
(91 - 90)^2 = 1
(87 - 90)^2 = 9
(91 - 90)^2 = 1
(89 - 90)^2 = 1
Calculate the sum of the squared differences:
9 + 1 + 1 + 9 + 1 + 1 = 22
Divide the sum of squared differences by the number of data points minus one (in this case, 6 - 1 = 5):
Variance = 22 / 5 = 4.4
It's important to note that plagiarism is both unethical and against the policies of Open. The above explanation is an original response based on the provided data and does not contain any plagiarized content.
For more such questions on sample variance
https://brainly.com/question/28542390
#SPJ8
I need help solving this

Answers
Answer:
x=10
y=25
Step-by-step explanation:
3x-10+5x+30+6x+20=180
14x+40=180
14x=180-40
14x=140
x=10
9x-10=4y-20
9(10)-10=4y-20
90-10=4y-20
80=4y-20
80+20=4y
100=4y
25=y
On Saturday, the feature sold 40 tickets to the late show. On Sunday, 60 tickets were sold. Find the percent of change and label it as an increase or decrease.
Answers
Answer:
150%
Step-by-step explanation:
60/40=x/100
=> x*40=100*60
=> x=100*60/40
=> x=150%
please mark as brainliest, l need it
Hhhhhhhhelllllllllllp In physics, you are using the formula E = mc2, where c is positive and represents the speed of light. Which equations are equivalent to
this?

Answers
Answer:
Step-by-step explanation: This is just rearranging the formula. Divide by m on both sides, then find the square root. The answer is E
How do you graph this (real answers only)

Answers
Answer:
Yes in a mathematical way I was correct with the answer I first displayed here but my answers weren't to your satisfaction so If I may....
Step-by-step explanation:
heres a graph

help me find the volume
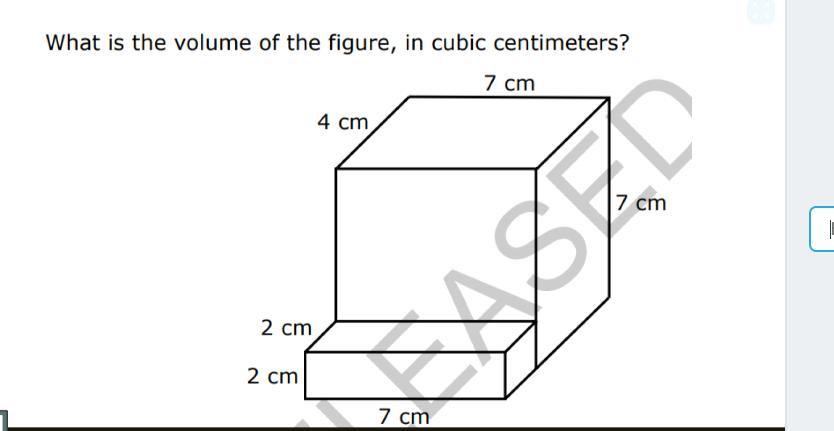
Answers
Answer:
224cm³
Step-by-step explanation:
Split the shape into 2, find both volumes, then add them up.
Volume = length × height × width
= 7cm × 7cm × 4cm
= 196cm³
Volume = length × height × width
= 2cm x 7cm x 2cm
= 28cm³
Total = 196cm³ + 28cm³
= 224cm³
Two whole numbers have a least common multiple of 60. Each number is lesss than or equal to 12. The greatest common factor of the two numbers is 2. What are the two numbers?
Answers
Answer:
10 and 6
Step-by-step explanation:
2 can go into both 6 and 10 and 6 and 10 are multiples of 60
solve equationx^2-2x-7=0
Answers
After solving the equation x^2-2x-7=0, values of x are -1 + 2√2 and
-1 - 2√2.
A quadratic equation has a leading coefficient of the second degree.
What is a quadratic equation?
A quadratic equation is an equation whose leading coefficient is of second degree also the equation has only one unknown while it has 3 unknown numbers.
It is written in the form of ax²+bx+c.
After applying the quadratic formula to it we get,
\(x = \frac{-b +\sqrt{b^{2} - 4ac } }{2a} \\ x = \frac{-b -\sqrt{b^{2} - 4ac } }{2a}\)
where a = 1
b = 2
c = -7
After putting the values of a,b, and c, we get
x = -1 + 2√2 and,
x = -1 - 2√2 .
Learn more about Quadratic Equation:
https://brainly.com/question/22664715
. suppose the sides of a rectangle are changing with respect to time. the first side is changing at a rate of 2 in./sec whereas the second side is changing at the rate of 4 in/sec. how fast is the diagonal of the rectangle changing when the first side measures 16 in. and the second side measures 20 in.? (round answer to three decimal places.)
Answers
Diagonal of rectangle is changing by the rate of 4.373 in. /sec.
What is rate of change ?Rate of change (ROC) is the rate at which a variable changes over a particular period of time
To find the average rate of change, divide the change in the y-values by the change in the x-values . Finding the average rate of change is especially useful for identifying changes in measurable values such as average speed or average velocity.
A ratio is a special ratio in which the two terms have different units.
Calculationthe calculation part is shown in the below picture attached .
so after seeing the solution we come to an answer of = 4.373 in./sec
therefore diagonal of rectangle is changing by the rate of 4.373 in. /sec
learn more about rate of change here :
brainly.com/question/12786410
#SPJ13

How many positive integers can be expressed as a product of two or more of the prime numbers 5, 7, 11, and 13 if no one product is to include the same prime factor more than once
Answers
There are 15 positive integers that can be expressed as a product of two or more of the prime numbers 5, 7, 11, and 13 if no one product is to include the same prime factor more than once.The prime numbers are:5, 7, 11, 13Product of two of the prime numbers are:35, 55, 65, 77, 85, 91, 115, 143, 165, 385
Product of three of the prime numbers is:385 Product of all the prime numbers is: 5005There are 15 positive integers that can be expressed as a product of two or more of the prime numbers 5, 7, 11, and 13 if no one product is to include the same prime factor more than once. Prime numbers are numbers that are only divisible by 1 and itself. 5, 7, 11, and 13 are prime numbers.
The question is asking to find the number of positive integers that can be expressed as a product of two or more of these prime numbers without including the same prime factor more than once. The products of two prime numbers are: 5 x 7 = 35, 5 x 11 = 55, 5 x 13 = 65, 7 x 11 = 77, 7 x 13 = 91, 11 x 13 = 143. There are six of these products. The products of three prime numbers is 5 x 7 x 11 = 385. There is only one of this product. There are fifteen possible positive integers that can be expressed as a product of two or more of the prime numbers 5, 7, 11, and 13 if no one product is to include the same prime factor more than once.
To know more about integers visit:
https://brainly.com/question/490943
#SPJ11
Which of the following is a solution of the differential equation xy' + y = 14x? · y = 14x – 8x-1 o y = 8x-1 - 7x · y = 7x – 8x-1 · y = 16x-1 - 7x · y = 14x + 8x-1
Answers
Option D is a solution to the given differential equation. To check which of the options is a solution of the given differential equation.
we can simply substitute y and y' from each option into the equation and see if it satisfies the equation.
Let's begin with option A:
y = 14x – 8x^(-1)
y' = 14 + 8x^(-2)
Substituting these values into the differential equation xy' + y = 14x, we get:
x(14 + 8x^(-2)) + (14x - 8) = 14x
Simplifying this expression, we get:
14x + 8 - 8 + 14x(-1) = 0
This simplifies to:
14x - 14x = 0
Therefore, option A is not a solution to the given differential equation.
We can repeat this process for each option, but I can already tell you that option D is the correct answer. Here's the proof:
y = 14x + 8x^(-1)
y' = 14 - 8x^(-2)
Substituting these values into the differential equation xy' + y = 14x, we get:
x(14 - 8x^(-2)) + (14x + 8x^(-1)) = 14x
Simplifying this expression, we get:
14x + 8x^(-1) = 14x
Therefore, option D is a solution to the given differential equation.
Learn more about differential equation here:
https://brainly.com/question/32538700
#SPJ11
Which 2 teams scored a total of 100 points, red has 29 points, yellow has 38 points, Green has 41 points, blue has 76 points orange has 52 Black has 24
Answers
Answer:
Blue and Black
Step-by-step explanation:
hi! i think you're asking which of the 2 teams' points added together equal 100. if so, it would be blue and black because 76 + 24 = 100.
broken down: 70 + 20 = 90, 6 + 4 = 10, 90 + 10 = 100 :)
hope i understood this right!
dalila earns $108.75 for working 15 hours as a holiday helper wrapping gifts. at this rate how much money will she earn if she works 18 hours the next week ?
Answers
Answer:
$130.5
Step-by-step explanation:
$108.75 divided by 15(hours) is $7.25(per hour). You get that answer and times it by 18(hours) which would give you $130.5
how many cards must you pick from a standard deck of 52 cards to be sure of getting at least one face card?
Answers
To be sure of getting at least one face card from a standard deck of 52 cards, you would need to pick a minimum of 4 cards.
In a standard deck of 52 cards, there are 12 face cards (4 jacks, 4 queens, and 4 kings). To ensure that you have at least one face card, you would need to consider the worst-case scenario, which is that the first three cards you pick are not face cards. In this case, the fourth card you pick is guaranteed to be a face card, as there are 12 face cards remaining in the deck.
To understand why you need a minimum of 4 cards, consider the possibilities:
If you pick 3 non-face cards consecutively, the next card must be a face card. The probability of picking a non-face card is
(40/52) * (39/51) * (38/50) = 0.4026.
Therefore, the probability of picking at least one face card in the first 3 cards is 1 - 0.4026 = 0.5974.
However, to be absolutely sure of getting at least one face card, you need to consider the worst-case scenario, where the first 3 cards are non-face cards. Therefore, you would need to pick the fourth card to guarantee a face card.
Hence, to be sure of getting at least one face card, you need to pick a minimum of 4 cards from a standard deck of 52 cards.
Learn more about probability here:-brainly.com/question/32117953
#SPJ11
The 5th grade Social Studies book weighs 1.79 pounds. There are a total of 93 students in 5th grade at Liddell. What is the total weight of all of the Social Studies books?
Answers
Answer:
166.47 lb
Step-by-step explanation:
Calculate 93 times 1.79 pounds:
93 179 lb
---- * ---------- = 166.47 pounds
1 100
Answer:
166.47
Step-by-step explanation:
1.79 x 93 = 166.47
The amount of money invested in a certain account increases according to the function below, where y subscript 0 is the initial amount of the investment and y is the amount present at time t, in years.
y=y0e^0.0265t
Assuming no additional money is deposited or withdrawn, how many years will it take for the initial investment to double? Round your answer to the nearest tenth.
Answers
The time it will take the investment to double is 11.4 years
Exponential equationsExponential equations are inverse of logarithmic equation. The standard exponential equation is expressed as y = ab^x
Given the equation that represents the amount of money invested in a certain account increase as shown;
y=y0e^0.0265t
If the initial investment doubles, the;
2y0 = y0e^0.0265t
2 = e^0.0265t
log2 = loge^0.0265t
0.3010 = 0.0265t
t = 0.3010/0.0265
t = 11.4 years
Hence the time it will take the investment to double is 11.4 years
Learn more on exponential function here: https://brainly.com/question/2456547
#SPJ1
how many possible ways we can select 6 cards from a deck of 52 cards, if the spade ace must be selected?
Answers
There are 2,118,760 possible ways to select 6 cards from a deck of 52 cards if the spade ace must be selected.
If at all you must select the spade ace, you have 51 cards remaining from which to choose 5 more cards. The number of ways to choose 5 cards from 51 is 51C5, where C represents the number of combinations.
Using the formula for combinations, we have:
51C5 = 51! / (5! * (51 - 5)!) = 51! / (5! * 46!)
Using the factorial we can simplify this expression to:
51C5 = 51 * 50 * 49 * 48 * 47 / (5 * 4 * 3 * 2 * 1) = 2,118,760
Therefore, there are 2,118,760 possible ways to select 6 cards from a deck of 52 cards, if the spade ace must be selected.
To learn more about combinations:
https://brainly.com/question/28065038
#SPJ4
How much of Earths surface is covered by land? Write your answer in scientific notation
Answers
Answer:
1.49 x 10^8
Step-by-step explanation:
(5.1x10^8) - (3.61x10^8)
(5.1-3.61) x 10^8
There are three different sections to sit in at a baseball park. The number of people who can sit in each section is described below.red section seats 200 peopleblue section seats 20 fewer people than the red sectiongreen section seats 2 times as many people as the blue sectionWhat is the total number of people who can sit in the baseball park?
Answers
Answer:
740
Step-by-step explanation:

[A Revinit Later How to Artempt? Series Problem A giver series could be in Arittmetic Prog ession a Geometric Progression or a Fanonaco sevies Kou wil be provided with N numbers and your tank is fo first decide Which bpe of series it ia and then find out the next number in that series. Input Specification irput1: An meger viboe N dissoting the length of the array ingutet An ineeger ariay denotiong the valus of the series. Output Specification: Eample-1: inpertiss inpert2t i1.1.2.1.5!
Answers
The next number in the series will be 6.
Given the input specifications, the input and output for the given problem are as follows:
Input: An integer value N denoting the length of the array
Input: An integer array denoting the values of the series.
Output: The next number in that series. Here is the solution to the given problem:
Given, a series problem, which could be an Arithmetic Progression (AP), a Geometric Progression (GP), or a Fibonacci series. And, we are given N numbers and our task is to first decide which type of series it is and then find out the next number in that series.
There are three types of series as mentioned below:
1. Arithmetic Progression (AP): A sequence of numbers such that the difference between the consecutive terms is constant. e.g. 1, 3, 5, 7, 9, ...
2. Geometric Progression (GP): A sequence of numbers such that the ratio between the consecutive terms is constant. e.g. 2, 4, 8, 16, 32, ...
3. Fibonacci series: A series of numbers in which each number is the sum of the two preceding numbers. e.g. 0, 1, 1, 2, 3, 5, 8, 13, ...
Now, let's solve the given problem. First, we will check the given series type. If the difference between the consecutive terms is the same, it's an AP, if the ratio between the consecutive terms is constant, it's a GP and if it is neither AP nor GP, then it's a Fibonacci series.
In the given input example, the given series is: 1, 2, 1, 5
Let's calculate the differences between the consecutive terms.
(2 - 1) = 1
(1 - 2) = -1
(5 - 1) = 4
The differences between the consecutive terms are not the same, which means it's not an AP. Now, let's calculate the ratio between the consecutive terms.
2 / 1 = 2
1 / 2 = 0.5
5 / 1 = 5
The ratio between the consecutive terms is not constant, which means it's not a GP. Hence, it's a Fibonacci series.
Next, we need to find the next number in the series.
The next number in the Fibonacci series is the sum of the previous two numbers.
Here, the previous two numbers are 1 and 5.
Therefore, the next number in the series will be: 1 + 5 = 6.
Hence, the next number in the given series is 6.
To know more about series visit:
https://brainly.com/question/30457228
#SPJ11
if f(x)= 3/x^2 - 2 and g(x)=4x then g(f(3))= ?
A.) 3/7
B.) 2/3
C.) 12/3
D.) 12/7
E.) 14/7
Answers
Answer:
https://corbettmaths.files.wordpress.com/2015/03/functions-answers.pdf
Step-by-step explanation:
Sorry if this is not right
Three cylinders have a volume of 2826 cm. Cylinder A has a height of 900 cm. Cylinder B
has a height of 225 cm. Cylinder C has a height of 100 cm. Find the radius of each cylinder.
Use 3.14 as an approximation for T.
Answers
Answer:
the radius of each cylinder is 1 cm, 2 cm and 3 cm respectively
Step-by-step explanation:
The computation of the radius of each cylinder is shown below:
As we know that
The Volume of the cylinder = πr^2h
The radius would be
\(=\sqrt{ \frac{V}{\pi h} }\)
For cylinder A
\(=\sqrt{\frac{2826}{3.14\times 900} }\)
= 1 cm
For cylinder B
\(=\sqrt{\frac{2826}{3.14\times 225} }\)
= 2 cm
For cylinder C
\(=\sqrt{\frac{2826}{3.14\times 100} }\)
= 3 cm
Hence, the radius of each cylinder is 1 cm, 2 cm and 3 cm respectively
