Corinne tends to be a spender. Luckily, her employer offers retirement saving options for the workers. Which of the following is the best option for Corinne to start saving for retirement
now?
A. A money market account
B. A simple savings account
C. A prepaid plan
D. A matching benefit
Answers
Related Questions
Determine an interval that a root of
f(x)=5cosx)−√x^2 +1+2^x−1
lies on
Answers
The root of the function \(\(f(x) = 5\cos(x) - \sqrt{x^2 + 1} + 2^{x-1}\)\) lies within the interval \(\([-1, 0]\)\).
To find the interval where the root of the given function lies, we need to analyze the behavior of the function within certain intervals. Let's consider the interval \(\([-1, 0]\)\).. For \(\(x = -1\)\), we have \(\(f(-1) = 5\cos(-1) - \sqrt{(-1)^2 + 1} + 2^{-2}\)\). Since \(\(\cos(-1)\)\) is positive and the other terms are also positive, the value of \(\(f(-1)\)\) is positive.
Now, for \(\(x = 0\)\), we have \(\(f(0) = 5\cos(0) - \sqrt{0^2 + 1} + 2^{-1}\)\). Since \(\(\cos(0)\)\) is positive and the other terms are positive, the value of \(\(f(0)\)\) is positive.
As the function is continuous, and it changes sign from positive to negative within the interval \(\([-1, 0]\)\) (as \(\(f(-1)\)\) and \(\(f(0)\)\) have different signs), by the Intermediate Value Theorem, there exists at least one root of the function within this interval. Therefore, we can conclude that the root of \(\(f(x)\)\) lies within the interval \(\([-1, 0]\)\).
To learn more about function refer:
https://brainly.com/question/25638609
#SPJ11
write an equation for the circle described. center (2,-1) and contains the point (4,5) the equation is?
Answers
the volume of a cuboid is 1200 centimetre cube the height is 8cm and breadth is 10cm then find its length
Answers
Answer:
Volume= Length ×breadth ×height
L=V/b×h
L=1200/80
L=15cm
A cylinder can have a volume of 16πcm ^3
. Use LaGrange multipliers to determine the dimensions of the can that yield the minimum surface area. a. What is the radius of the can with the minimum surface area? b. What is the height of the can with the minimum surface area?
Answers
The dimensions of the cylinder with the minimum surface area for a volume of 16π cm^3: a. The radius is 2 cm. , b. The height is 4 cm.
a. The radius of the can with the minimum surface area can be found by setting up the optimization problem with the objective function as the surface area of the cylinder, subject to the constraint of the volume of the cylinder. By applying Lagrange multipliers, we can find the critical points. By solving the system of equations, we can find the value of the radius.
b. Similarly, the height of the can with the minimum surface area can also be found by setting up the optimization problem with the objective function as the surface area of the cylinder, subject to the constraint of the volume of the cylinder. By applying Lagrange multipliers, we can find the critical points. By solving the system of equations, we can find the value of the height.
By solving these optimization problems using Lagrange multipliers, we can determine the specific values of the radius and height that yield the minimum surface area for the given volume of the cylinder.
Learn more about Lagrange multipliers here:
https://brainly.com/question/30776684
#SPJ11
HELP PLEASE, if work is needed please add if THANK YOU!!!

Answers
a. If 4 - 5i and -√3 are roots of the polynomial, the other two roots are
4 + 5i and √3b. If polynomial P(x) is divided by x - a, the remainder is zero, then a. x - a is a factor of the polynomial P(x)
What is a polynomial?A polynomial is a mathematical function in which the least power of the variable is 2.
a. Suppose that a polynomial function has four roots and two of its roots are 4 - 5i and -√3. We desire the other two roots. We proceed as follows.
We know that know that complex roots and irrational roots of a polynomial occur in conjugate pairs.
So, since 4 - 5i and -√3 are roots of the polynomial, then their conjugate pairs are also roots.
So, the conjugate pairs are
4 + 5i and √3So, the other two roots are
4 + 5i and √3b. A polynomial P(x) is divided by x - a, the remainder is zero. What can we conclude?
Using the factor theorem, if p(x) is a polynomial and x - a is a linear factor, then if x - a is a factor of p(x), then the remainder when p(x) is divided by x - a is zero.
So, from the above since the remainder when P(x) is divided by x - a is zero, then x - a is a factor of P(x)
So, the answer is a. x - a is a factor of the polynomial P(x)
Learn more about polynomial here:
https://brainly.com/question/28947270
#SPJ1
HELPP this is the last question I need to answer asap
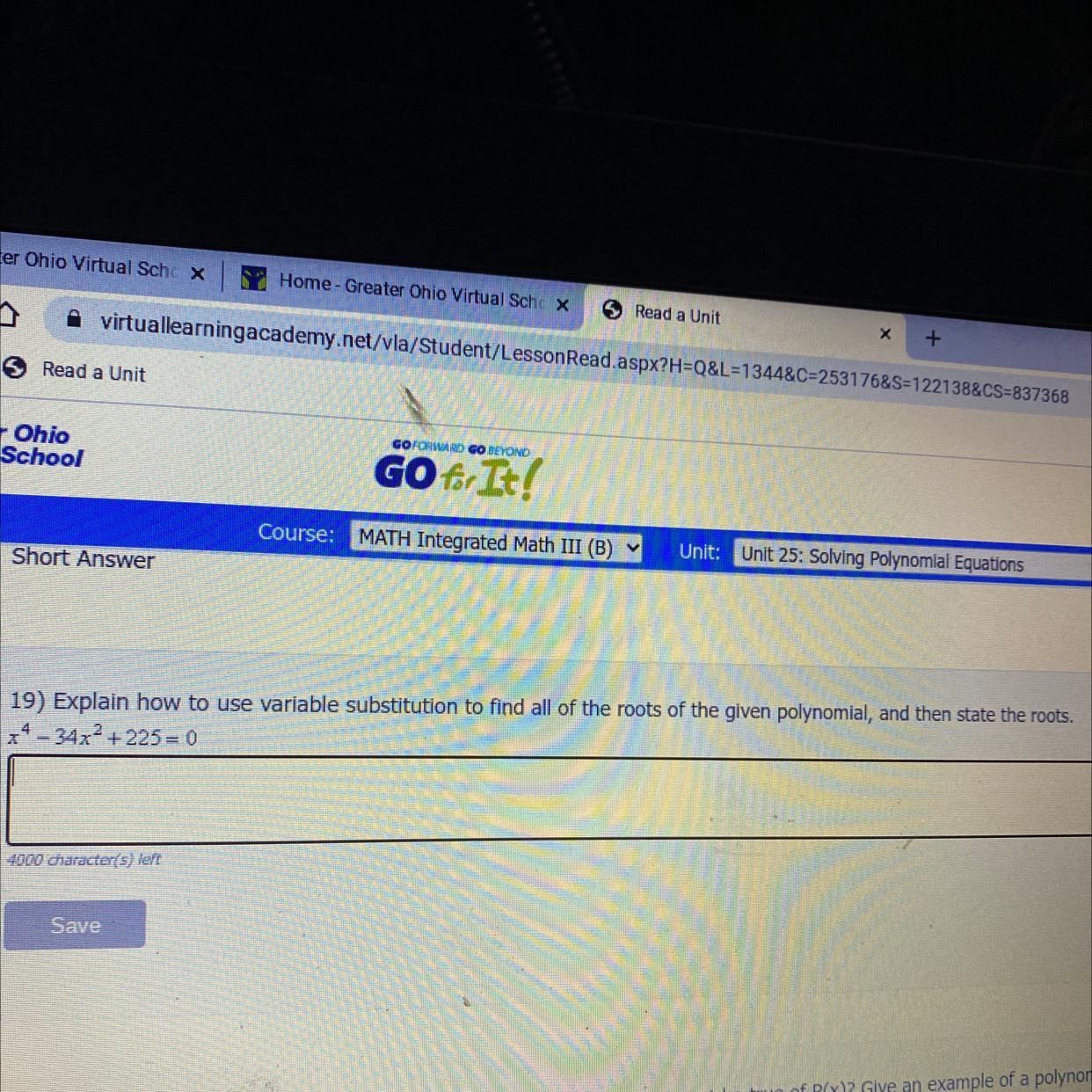
Answers
Answer:
x = 5, -5, 3, -3
Step-by-step explanation:
First, substitute u = x^2 into the equation, and we have
u^2 - 34u + 225 = 0
u = x^2
Factor u^2 −34u +225 using the AC method, and we get
( u - 25) ( u - 9) = 0
We know If any individual factor on the left side of the equation is equal to
0, the entire expression will be equal to 0, so
u - 25 = 0
u - 9 = 0
Next, we set u - 25 equal to 0 and solve for u, and we get
u = 25
Then set u - 9 equal to 0 and solve for u, and we get
u = 9
The final solution is all the values that make (u−25)(u−9) = 0 true.
u =25,9
Substitute the real value of u=x^2 back into the solved equation.
x^2 = 25
(x^2)^1 = 9
x^2 = 25
x = 5, -5
Now we solve the second equation
(x^2)^1 = 9
x = 3, -3
So, the answers are: 5, -5, 3, -3
Which reason justifies step 6 below?
Use the diagram.


Answers
The congruence theorem that justifies the similar triangles of triangles EFH and GFH is given as follows:
D. AAS.
Why the two triangles are similar?For the triangles EFH and GFH in this problem, we have that:
The angles E and G have the same measure.The right angles have the same measure.The side lengths HF is the same, by the reflective property of congruence.These three features are used to identify the congruence theorem as follows.
Then the congruence theorem that justifies the similar triangles of triangles EFH and GFH is the Angle-Angle-Side theorem, given by option D, as:
Two angles, the bottom angles and the right angle have the same measure.The non-included side HF has the same measure.More can be learned about congruence theorems at https://brainly.com/question/29994750
#SPJ1
Im du.mb at this stuff, i dont know how to do it

Answers
Answer:
the correct answer will be 88
Answer:
Area of the shaded region 45.76 cm².
Step-by-step explanation:
Firstly, finding the area of rectangle by substituting the values in the formula :
\({\longrightarrow{\pmb{\sf{A_{(Rectangle)} = l \times b}}}}\)
→ A = Area→ l = length → b = breadth\(\begin{gathered} \qquad{\longrightarrow{\sf{A_{(Rectangle)} = l \times b}}}\\\\\qquad{\longrightarrow{\sf{A_{(Rectangle)} = 12\times 8}}}\\\\\qquad{\longrightarrow{\sf{A_{(Rectangle)} = 96}}}\\\\\qquad{\star{\boxed{\sf{\pink{A_{(Rectangle)} = 96 \: {cm}^{2}}}}}} \end{gathered}\)
Hence, the area of rectangle is 96 cm².
\(\rule{200}2\)
Secondly, finding the area of circle by substituting the values in the formula :
\({\longrightarrow{\pmb{\sf{A_{(Circle)} = \pi{r}^{2}}}}}\)
→ A = Area → π = 3.14 → r = radius\(\begin{gathered} \qquad{\longrightarrow{\sf{A_{(Circle)} = \pi{r}^{2}}}} \\ \\ \qquad{\longrightarrow{\sf{A_{(Circle)} = 3.14{(4)}^{2}}}} \\ \\ \qquad{\longrightarrow{\sf{A_{(Circle)} = 3.14{(4\times 4)}}}} \\ \\ \qquad{\longrightarrow{\sf{A_{(Circle)} = 3.14(16)}}} \\ \\ \qquad{\longrightarrow{\sf{A_{(Circle)} = 3.14 \times 16}}} \\ \\ \qquad{\longrightarrow{\sf{A_{(Circle)} \approx 50.24}}} \\ \\ \qquad{\star{\boxed{\sf{\purple{A_{(Circle)} \approx 50.24 \: {cm}^{2}}}}}} \end{gathered}\)
Hence, the area of circle is 50.24 cm².
\(\rule{200}2\)
Now, finding the area of shaded region by substituting the values in the formula :
\(\longrightarrow{\pmb{\sf{A_{(Shaded)} = A_{(Rectangle)} - A_{(Circle)}}}}\)
→ A = Area→ Rectangle → Circle\(\begin{gathered}{\quad{\longrightarrow{\sf{A_{(Shaded)} = A_{(Rectangle)} - A_{(Circle)}}}}}\\\\{\quad{\longrightarrow{\sf{A_{(Shaded)} = 96 - 50.24}}}}\\\\{\quad{\longrightarrow{\sf{A_{(Shaded)} \approx 45.76}}}}\\\\{\quad{\star{\boxed{\sf{\red{A_{(Shaded)} \approx 45.76 \: {cm}^{2}}}}}}} \end{gathered}\)
Hence, the area of shaded region is 45.76 cm².
\(\rule{300}{2.5}\)
Find a vector function r(t), that represents the curve of intersection of the two surfaces. the cylinder x2 y2=36 and the surface z=4xy
Answers
Given:
\(\begin{aligned}&x^2+y^2=16 \\&z=x y\end{aligned}\)
Express 16 as \(4^{2}\): \(x^2+y^2=16\)
\(x^2+y^2=4^2\\x^2+y^2=4^2 \times 1\)
Trignometry,
\(\cos ^2(t)+\sin ^2(t)=1\)
Now, substitute \(\cos ^2(t)+\sin ^2(t)\) for 1:
\(\begin{aligned}&x^2+y^2=4^2 \times 1 \\&x^2+y^2=4^2 \times\left[\cos ^2(t)+\sin ^2(t)\right]\end{aligned}\\x^2+y^2=4^2 \times \cos ^2(t)+4^2 \times \sin ^2(t)\)
Law of indicates:
\(\begin{aligned}&x^2+y^2=[4 \times \cos (t)]^2+[4 \times \sin (t)]^2 \\&x^2+y^2=[4 \cos (t)]^2+[4 \sin (t)]^2\end{aligned}\\x^2=[4 \cos (t)]^2 \text { and } y^2=[4 \sin (t)]^2\)
Taking positive square roots as follows:
\(x=4 \cos (t), y=4 \sin (t)\)
Recall that, z = xy.
Now, we have:
\(\begin{aligned}&z=4 \cos (t) \times 4 \sin (t) \\&z=16 \cos (t) \cdot \sin (t)\end{aligned}\)
Now, substitute the values:
\(r(t)=x_t i+y_t j+z_t k\)
So, the vector r(t) is: \(r(t)=(4 \cos (t)) i+(4 \sin (t)) i+(16 \cos (t) \cdot \sin (t)) i\)
Therefore, the vector function r(t) is written as: \(r(t)=x_t i+y_t j+z_t k\)
Know more about vector functions here:
https://brainly.com/question/14895420
#SPJ4
f(x,y)=−4x2+4xy−2y2+6x+8y Suppose that there is a constraint such that xy≤15, What is the value of y that optimizes the function? Question 17 f(x,y)=−4x2+4xy−2y2+6x+8y Suppose that there is a constraint such that xy≤15, what is the Lagrange Multiplier?
Answers
The value of y that optimizes the function is y = 3/2. The Lagrange Multiplier in this case is -105/8.
To optimize the function \(f(x, y) = -4x^2 + 4xy - 2y^2 + 6x + 8y\) subject to the constraint xy ≤ 15, we can use the method of Lagrange multipliers.
The Lagrangian function is defined as:
L(x, y, λ) = f(x, y) - λ(g(x, y) - 15)
where g(x, y) = xy is the constraint equation.
To find the optimal value of y, we need to solve the following system of equations:
∂L/∂x = -8x + 4y + 6 - λy = 0 (1)
∂L/∂y = 4x - 4y + 8 - λx = 0 (2)
g(x, y) - 15 = xy - 15 = 0 (3)
From equation (1), we can rearrange it as:
-8x + 4y - λy = -6 (4)
From equation (2), we can rearrange it as:
4x - 4y - λx = -8 (5)
To solve this system of equations, we can eliminate λ by multiplying equation (4) by x and equation (5) by y, and then subtracting the resulting equations:
\(-8x^2 + 4xy - λxy = -6x (6)\\4xy - 4y^2 - λxy = -8y (7)\)
Subtracting equation (7) from equation (6), we get:
\(-8x^2 + 4xy - 4y^2 = -6x + 8y\)
Simplifying this equation gives:
\(-8x^2 - 4y^2 + 4xy = -6x + 8y\)
Rearranging terms, we have:
\(-8x^2 + 4xy + 6x - 4y^2 - 8y = 0\)
Factoring, we get:
(2x - y)(-4x - 2y + 6) = 0
Setting each factor equal to zero gives:
2x - y = 0 (8)
-4x - 2y + 6 = 0 (9)
From equation (8), we can solve for y:
y = 2x (10)
Substituting equation (10) into equation (9), we get:
-4x - 4x + 6 = 0
Simplifying, we have:
-8x + 6 = 0
Solving for x, we find:
x = 3/4
Substituting this value of x into equation (10), we can find y:
y = 2 * (3/4) = 3/2
Therefore, the value of y that optimizes the function is y = 3/2.
To find the Lagrange Multiplier, we substitute the optimal values of x and y into the constraint equation (3):
xy - 15 = (3/4) * (3/2) - 15 = 9/8 - 15 = -105/8
Hence, the Lagrange Multiplier is -105/8.
To know more about Lagrange Multiplier,
https://brainly.com/question/32575503
#SPJ11
state how to use a line integral to determine the arc length of a curve c. provide a brief example of a curve that is not part of a circle and calculate its arc length.
Answers
Therefore, integrate the norm of the curve's tangent vector over a specified interval. An example curve could be y = x^2, with the arc length calculated by integrating the square root of 1 + (2x)^2 over a given interval.
A line integral can determine the arc length of a curve c by integrating the norm of the curve's tangent vector over a specified interval. The formula for arc length is given by the integral of the middle of the curve's derivative with respect to its parameter. This involves taking the square root of the sum of the squares of the components of the derivative and integrating this result over the interval of interest. An example of a curve that is not part of a circle could be the curve defined by the equation y = x^2. To calculate its arc length, we would first need to find its derivative, which is y' = 2x. Then, we would integrate the square root of 1 + (2x)^2 over the interval of interest, such as from x = 0 to x = 2.
Therefore, integrate the norm of the curve's tangent vector over a specified interval. An example curve could be y = x^2, with the arc length calculated by integrating the square root of 1 + (2x)^2 over a given interval.
Learn more about the confidence interval here:
https://brainly.com/question/20309162
#SPJ11
O(Q0) A(2,0), B(3, 2) and C(1, 2) are the vertices of quadrilateral OABC. Translate quadrilateral by translation vector [0,2]
Answers
Answer:
A'(2,2) B'(3,4) C'(1,4) O'(Q,2)
Find the value of x PLS ANSWER THIS ASAP I WILL MARK THE BRAINIEST

Answers
Answer:
Answer: B. x=7
Step-by-step explanation:
Similar Triangles
Assuming the up arrows indicate parallel lines, then triangles PQT and PRS are similar. See the image provided below.
Similar triangles have their side lengths proportional by a constant scale factor. They also have all of their internal angles congruent, or with the same measure.
This means that the marked angles are equal:
2x + 5 = x + 12
Subtracting x
x + 5 = 12
Subtracting 5:
x = 7
Answer: B. x=7

What is the slope of the line

Answers
Answer:
-2
Step-by-step explanation:
What is 0.4 in fraction form?
Answers
Answer: 4/10
Step-by-step explanation:
4/10
Let's check
\(\\ \rm\rightarrowtail 0.4\)
\(\\ \rm\rightarrowtail 4/10\)
\(\\ \rm\rightarrowtail 2/5\)
santa has 300 he share. 1/5 3/10 50.00 he bank the rest what fraction did he bank
Answers
Answer:
1/6
Step-by-step explanation:
$50 is 1/6 of $300
(I think this is what you meant. The question was kind of confusing.)
Three side lengths of a right triangle are given which side length should you substitute for the hypotenuse in Pythagorean theorem
Answers
In the Pythagorean theorem, a²+b²=c² is the formula for finding the missing side length in a right-angled triangle. This formula is useful for determining one of the missing side lengths of a right triangle if you know the other two.
However, the theorem also states that c is the length of the triangle's hypotenuse. So, if you have a right-angled triangle with all three sides provided, you may use the Pythagorean theorem to solve for any of the missing sides. You'll use the hypotenuse length as the c variable when the three sides are given, then solve for the missing side.
To apply the Pythagorean theorem, you must identify the hypotenuse, which is the side opposite the right angle. If you're given three sides, the longest side is always the hypotenuse. As a result, you can always use the Pythagorean theorem to solve for one of the shorter sides by using the hypotenuse length.
You can learn more about the Pythagorean theorem at: brainly.com/question/14930619
#SPJ11
Which point was translated 3 units right from the orange point?
A
B
C

Answers
Answer:
Point A
Step-by-step explanation:
Point A is at ( -4, 4)
It was translated 3 units right, which means the x increased by 2.
So, the point is at (-2,4), and the answer is A.
A recent study reported that 45 percent of adults in the United States now get all their news online. A random sample of 8 adults in the United States will be selected. What is the probability that 6 of the selected adults get all their news online?
Answers
Answer:
7 percent
Step-by-step explanation:
The probability that 6 of the selected adults get all their news online will be 0.07.
What is binomial distribution?Frequency distribution of the percentage of successful outcomes that might occur in a certain number of trials with the same chance of success.
If X~B(n, p), then the probability is given as
\(\rm P(X=x) = \ ^nC_x \times p^x \times (1-p)^{n - x}\)
A new report revealed that 45% of grown-ups in the US presently get all their news on the web. An irregular example of 8 grown-ups in the US will be chosen.
The probability that 6 of the selected adults get all their news online will be given as,
P(x = 6) = ⁸C₆ × (0.45)⁶ × (1 - 0.45)²
Simplify the expression, then we have
P(x = 6) = ⁸C₆ × (0.45)⁶ × (1 - 0.45)²
P(x = 6) = 28 × (0.45)⁶ × (0.55)²
P(x = 6) = 0.07
More about the binomial distribution link is given below.
https://brainly.com/question/14565246
#SPJ2
Question is in the file below.

Answers
Answer:
I am confused with this ques there two of them gets the same ans
A and B has same value and
C and D has same value
are you supposed to choose two of. them?
however i got C= -40 , D = -40
Let me know if its incorrect :-)
I NEED HELP ASAP....................................................

Answers
Answer: what’s the question?
Step-by-step explanation:
dummy variable this might indicate that there are strong multicollinearity problems or that the design matrix is singular.
Answers
In statistical modeling, a dummy variable is used to represent categorical variables with two or more levels as binary variables (0 or 1).
The presence of a dummy variable in a model does not inherently indicate multicollinearity or singularity of the design matrix. Multicollinearity refers to a situation where two or more predictor variables in a regression model are highly correlated, making it difficult to distinguish their individual effects on the response variable. Multicollinearity can cause instability in the estimation of regression coefficients but is not directly related to the use of dummy variables.
Singularity of the design matrix, also known as perfect collinearity, occurs when one or more columns of the design matrix can be expressed as a linear combination of other columns. This can happen when, for example, a set of dummy variables representing different categories has one category that is completely determined by the others. In such cases, the design matrix becomes singular, and the regression model cannot be estimated.
To know more about dummy variable,
https://brainly.com/question/32456370
#SPJ11
can someone answer page 3 question 3, page 5 question 3, all of page 6
Answers
The answers to the questions involving trigonometry are: 90, BC/AB ÷ BC/AB = 1, g = 6.5, <I = 62 degrees, h= 13.8, 12.0, x = 6.8, x = 66.4, 160.6, The pole = 6.7
What is trigonometrical ratios?Trigonometric ratios are special measurements of a right triangle, defined as the ratios of the sides of a right-angled triangle. There are three common trigonometric ratios: sine, cosine, and tangent
For page 3 question 3,
a) <A + <B = 90 since <C = right angle
b) SinA = BC/AB and CosB = BC/AB
The ratio of the two angles BC/AB ÷ BC/AB = 1
I notice that the ratio of sinA and cosB gives 1
b) The ratio of CosA and SinB will give
BC/AB ÷ BC/AB
= BC/AB * AB/BC = 1
For page 5 number 3
Tan28 = g/i
g/12.2 = tan28
cross multiplying to have
g = 12.2*tan28
g = 12.2 * 0.5317
g = 6.5
b) the angle I is given as 90-28 degrees
<I = 62 degrees
To find the side h we use the Pythagoras theorem
h² = (12.2)² + (6.5)²
h² = 148.84 +42.25
h²= 191.09
h=√191.09
h= 13.8
For page 6
1) Sin42 = x/18
x=18*sin42
x = 18*0.6691
x = 12.0
2) cos28 = 6/x
xcos28 = 6
x = 6/cos28
x [= 6/0.8829
x = 6.8
3) Tan63 = x/34
x = 34*tan63
x= 34*1.9526
x = 66.4
4) Sin50 123/x
xsin50 = 123
x = 123/sin50
x = 123/0.7660
x =160.6
5) Sin57 = P/8
Pole = 8sin57
the pole = 8*0.8387
The pole = 6.7
Learn more about trigonometrical ratios on https://brainly.com/question/23130410
#SPJ1
use regression analysis to fit a parabola to y as a function of x and plot the parabola (line only) and the data (symbols only).(do not use polyfit.)
Answers
The regression analysis can be used to fit a parabola to a set of data and plot the parabola and data to visualize the relationship between x and y. By using regression analysis, we can find the best-fitting parabola and gain insights into the underlying trends in the data.
Regression analysis can be used to fit a parabola to a set of data by finding the coefficients of the quadratic equation y = ax^2 + bx + c that best fit the data. This can be done using least squares regression, where the sum of the squared differences between the predicted values of y and the actual values of y is minimized.
To plot the parabola and the data, we can use a graphing calculator or a spreadsheet program like Excel. First, we input the data points into the spreadsheet and then use the regression analysis tool to find the coefficients a, b, and c that best fit the data. Once we have the coefficients, we can plot the parabola using the equation y = ax^2 + bx + c.
After plotting the parabola, we can overlay the data points to see how well the parabola fits the data. If the parabola fits the data well, the data points should be clustered around the curve of the parabola. If the parabola does not fit the data well, there may be outliers or other factors that are affecting the relationship between x and y.
For such more questions on Regression analysis:
https://brainly.com/question/30328991
#SPJ11
Find the distance between the points (-9,6) and (3,6).
Answers
Answer:
12 untis
Step-by-step explanation:
12 units becaause on a graph you count from -9,6 to 3,6 which is 12 units.

Question 3(Multiple Choice Worth 2 points)
(07.02 LC)
What is the missing numerator?
two over three plus blank over six equals one and one sixth
3
5
6
9
Answers
Answer:
The answer is 3 for the above question
Which number should be added to
both sides of this quadratic equation
to complete the square?
(-3/2)² + 1 = x² − 3x + (-3/2)²

Answers
Answer:
9/4
Step-by-step explanation:
You want to know the value required to complete the square in the equation 1 = x² -3x.
PictureYour picture shows the required value: (-3/2)² = 9/4.
<95141404393>
A suit is on sale for $475, which is 76% of the regular price.
What is the regular price?
Answers
Answer:
The regular price of the suit was $625.
Step-by-step explanation:
First, convert 76% into a decimal by moving the decimal place over twice to get 0.76. Then, set up this equation:
475 ÷ 0.76 = 625
Now, we can check if this is right by setting up this equation:
0.76 x 625 = 475.
Yep! It checks out! Our final answer is $625.
May I have Brainliest please? My next rank will be the highest one: A GENIUS! Please help me on this journey to become top of the ranks! I only need 3 more brainliest to become a genius! I would really appreciate it, and it would make my day! Thank you so much, and have a wonderful rest of your day!
Write a polynomial function f of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros. Write the function in standard form. -2, 1, 3
Answers
Answer:
Step-by-step explanation:
A polynomial function of least degree that has rational coefficients, a leading coefficient of 1, and the given zeros -2, 1, 3 is (x- -2)(x-1)(x-3) = x^3 - 6x^2 + 11x - 6
10+[25-{22(19-13)}]÷(6÷3)
Answers
Answer:
bro add me in ff krishal0554T