DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA DA
Answers
Answer:
da de da da da de do re mi fa so la mi AAAAAAAAAAA
Step-by-step explanation:
I can speak the language of the gods xD
Related Questions
n+n+n=1 what is n?????
Answers
Answer:
1/3
Step-by-step explanation:
If you add all the n's, it would make 3n=1. Divide both sides by 3 and get n=1/3
Answer:
0.333 or 1/3
Step-by-step explanation:
0.333*3=1
find the measures of the angles of the triangle whose vertices are a = ( − 2,0), b = (2,1), and c = (1, − 2).
Answers
So the triangle has three equal angles of 60 degrees.
To find the measures of the angles of the triangle with vertices at (-2,0), (2,1), and (1,-2), we can use trigonometry.
Let's use the following notation:
a = (-2,0)
b = (2,1)
c = (1,-2)
First, we need to find the coordinates of the midpoint of line segment AB, which is the length of the hypotenuse of the triangle.
Using the Pythagorean theorem, we have:
\(c^2 = a^2 + b^2\\1^2 + (-2)^2 = 2^2 + 1^2\)
25 = 4 + 1
23 = 3
So the length of the hypotenuse is 3 units.
Next, we need to find the coordinates of the midpoint of line segment BC, which is the length of one of the legs of the triangle.
Again, using the Pythagorean theorem, we have:
\(b^2 = a^2 + c^2\\1^2 + (-2)^2 = 2^2 + 1^2\)
25 = 4 + 1
23 = 3
So the length of the leg of the triangle is 3 units.
Now, we can use the law of cosines to find the measures of the angles of the triangle.
Let's denote the angle between lines AB and BC as alpha, the angle between lines AB and AC as beta, and the angle between lines BC and AC as gamma.
Using the law of cosines, we have:
\(cos(alpha) = (b^2 + c^2 - a^2) / (2bc)\\cos(beta) = (a^2 + c^2 - b^2) / (2ac)\\cos(gamma) = (a^2 + b^2 - c^2) / (2ab)\)
We know that:
a = (-2,0)
b = (2,1)
c = (1,-2)
So we can substitute these values into the above equations:
\(cos(alpha) = (2^2 + (-2)^2 - (-2)^2) / (2(-2)1) = (2 + (-2) + 2) / (2(-2)1) = 4 / 3\\cos(beta) = ((-2)^2 + 2^2 - (-2)^2) / (2(-2)2) = (-2 + 4 + 2) / (2(-2)2) = -1\\cos(gamma) = (2^2 + 1^2 - 1^2) / (2(1)(-2)) = 2 + (-1) + (-1) / (2(1)(-2)) = 1\)
Now we can substitute these values into the Pythagorean theorem to find the length of the legs of the triangle:
sin(alpha) = length of leg 1 / (2bc)
sin(beta) = length of leg 2 / (2ac)
sin(gamma) = length of leg 2 / (2ab)
We know that:
a = (-2,0)
b = (2,1)
c = (1,-2)
So we can substitute these values into the above equations:
sin(alpha) = √(8) / (2(-2)1)
= √(8) / √(3)
= √(2)
sin(beta) = √(5) / (2(1)2)
= √(5) / √(3)
= √(2)
sin(gamma) = √(5) / (2(1)(-2))
= √(5) / 1
= √(5)
Therefore, the measures of the angles of the triangle are:
alpha = 60 degrees
beta = 60 degrees
gamma = 60 degrees
So the triangle has three equal angles of 60 degrees.
Learn more about triangle visit: brainly.com/question/28470545
#SPJ4
Let a1, a2, a3 ……..be a sequence defined by a1 = 1 and ak = 2ak-1 . Find a formula for an and prove it is correct using. Find a formula for an and prove it is correct using induction
Answers
The sequence defined by a1 = 1 and ak = 2ak-1 can be represented by the formula an = 2^(n-1). We can prove this formula is correct using mathematical induction.
To prove the formula an = 2^(n-1) for the sequence, we will use mathematical induction.
Base Case: For n = 1, a1 = 2^(1-1) = 2^0 = 1, which matches the initial condition of a1 = 1. Hence, the formula holds for the base case.
Inductive Step: Assume that the formula holds for some arbitrary value k, i.e., ak = 2^(k-1). We need to show that it holds for k+1, i.e., ak+1 = 2^k.
Using the recursive definition, we have ak+1 = 2ak = 2^(k-1+1) = 2^k.
Therefore, the formula holds for k+1 as well.
By the principle of mathematical induction, we have shown that the formula an = 2^(n-1) is correct for all positive integers n.
Learn more about mathematical induction here:
https://brainly.com/question/12393516
#SPJ11
help me solve this pls need it as soon as possible
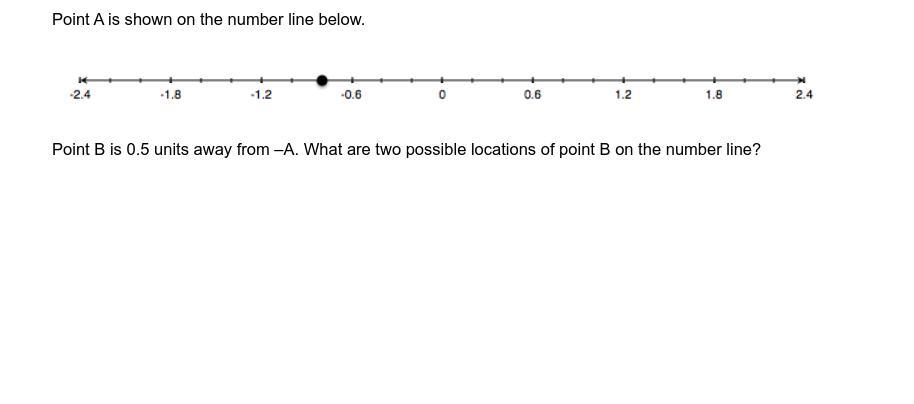
Answers
The two possible locations of point B on the number line are 0.1 and 1.1.
What is a number line?A number line is a graphic depiction of numbers organized in a straight line in mathematics. Positive numbers appear to the right of zero and negative numbers to the left of zero when it is displayed horizontally. At the line's intersection, the number zero serves as a standard against which other numbers' magnitudes can be measured.
Many forms of numbers, including whole numbers, integers, fractions, decimals, and even irrational numbers, can be represented on a number line. The distance between any two points on the number line, which stands for the difference between any two matching numbers, corresponds to a distinct number.
Number lines are frequently used to graph functions and equations as well as to execute basic arithmetic operations including addition, subtraction, multiplication, and division. They are also helpful for comprehending ideas like magnitude, distance, and absolute value.
To know more about the number line, visit:
https://brainly.com/question/24644930
#SPJ1
The lengths of the sides of a triangle are 3, 4, 5. Can the triangle be a right angle. Yes. No.
Answers
Answer:
Yes
Step-by-step explanation:
3 , 4 & 5 are Pythagorean Triplet numbers. When lengths of a triangle's 3 sides are Pythagorean Triplet , the triangle is a right angled triangle.
The triangle will be a right angled triangle only when the hypotenuse will have length of 5 and other 2 sides will have length of either 3 or 4.
Answer:
\(\boxed {\boxed {\sf Yes, \ the \ side \ lengths \ 3, \ 4, \ and \ 5\ can \ make \ a \ right \ triangle}}\)
Step-by-step explanation:
If the triangle is a right triangle, then the sides will check out in the Pythagorean Theorem.
\(a^2+b^2=c^2\)
Where a and b are the legs and c is the hypotenuse.
1. Define Sides
The legs are the 2 shorter sides and the hypotenuse is the longest.
The sides given are 3, 4 (shorter), and 5 (longest). Therefore:
\(a=3 \\b=4 \\c=5\)
2. Check the Sides in the Theorem
Substitute the values into the theorem.
\((3)^2+(4)^2=(5)^2\)
Solve according to PEMDAS: Parentheses, Exponents, Multiplication, Addition, and Subtraction.
Solve all of the exponents first.
(3)² = 3*3= 9 (4)²= 4*4= 16\(9+16=(5)^2\)
(5)²= 5*5= 25\(9+16=25\)
Add the numbers on the left side of the equation.
\(25=25\)
This is true. 25 is equal to 25, so this triangle can be a right triangle.
solve for m
8m=4 simplify
Answers
Answer:
Isolate the mDivide both sides by 8:Simplify the fraction:Find the greatest common factor of the numerator and denominator:Factor out and cancel the greatest common factor:
Then you get m=1/2
Step-by-step explanation:
Survey: 100 people were asked if they like dogs or cats. Using the two-way table, what percent of the females only said they like cats?
A. 48/100 = 48%
B. 39/100 = 39%
C. 39/48 = 81%
D. 49/100 = 49%

Answers
Answer:
C. 39/48 = 81%
Step-by-step explanation:
To determine the percentage of females who only said they like cats using the given two-way table, we need to find the number of females who selected "cats" only and divide it by the total number of females surveyed. We can then multiply the result by 100 to get the percentage.
According to the provided two-way table:
Number of females who only said they like cats = 39
Total number of females surveyed = 48
To calculate the percentage:
Percentage of females who only said they like cats = (Number of females who only like cats / Total number of females surveyed) * 100
Percentage of females who only said they like cats = (39 / 48) * 100 ≈ 81.25%
Therefore, the correct option is:
C. 39/48 = 81%
you randomly choose one shape from the bag. find the number of ways the event can occur. find the favorable outcomes of the event

Answers
(a) The number of ways that the event can occur is 6.
(b) Probabilities are :
1) 1/2, 2) 1/6 and 3) 1/3.
(a) Given a bag of different shapes.
Total number of shapes = 6
So, if we select one shape from random,
total number of ways that the event can occur = 6
(b) Number of squares in the bag = 3
Probability of choosing a square = 3/6 = 1/2
Number of circles in the bag = 1
Probability of choosing a circle = 1/6
Number of stars in the bag = 2
Probability of choosing a star = 2/6 = 1/3
Hence the required probabilities are found.
Learn more about Probability here :
https://brainly.com/question/14210034
#SPJ1
What is 12x³ – 9x² – 4x + 3 in factored form? hurry...
Answers
Answer:
Combine Like Terms:
=1728+−9x^2+−4x+3
=(−9x^2)+(−4x)+(1728+3)
= −9x^2+−4x+1731
Consider and economy with a single (representative) agent, with utility function
u(x,l)=(x^2/3)(l^1/3)
and an endowment of 0 units of x and 1 unit of l. The agent owns a firm that produces good x using l as an input with cost function
c(q)=q^2
Find the competitive prices and allocation.
Answers
The competitive price of good x and the corresponding allocation of labor (l) is \((2/3)^{(3/2)}\) x \(l^{(1/2)}\) = 1/2.
To find the competitive prices and allocation in this economy, we need to determine the equilibrium conditions. In a competitive market, prices are determined such that supply equals demand. In this case, the supply of good x is determined by the cost function of the firm, while the demand for good x is determined by the utility function of the representative agent.
Let's find the agent's demand for good x. The agent maximizes their utility subject to their budget constraint, which is given by the endowment of labor (l) and the prices of x and l. The agent's optimization problem can be solved using Lagrange multipliers, which yields the following demand function:
x = \((2/3)^{(3/2)}\) x \(l^{(1/2)}\)
We can find the supply of good x by minimizing the cost function of the firm. The cost minimization problem can be solved by equating the marginal product of labor to the wage rate (the price of labor). In this case, the marginal product of labor is equal to 2q, and the wage rate is 1. Solving for the quantity of x produced (q) gives us:
q = 1/2
We can determine the competitive prices. Since the demand for good x is given by the agent's utility function, we can equate the demand and supply functions to find the equilibrium prices:
\((2/3)^{(3/2)}\) x \(l^{(1/2)}\) = 1/2
Learn more about Lagrange multipliers here:
https://brainly.com/question/30776684
#SPJ4
Select the place where the digit 6 sits in this number. 607,182
Answers
Answer:
Hundred Thousand
Step-by-step explanation:
Hundred Thousand
I hope it helped you
Answer:
Hundred thousand
Step-by-step explanation:
The digit 6 is in the hundred thousand place.
To understand place values, see the attached file.
\(\rule[225]{225}{2}\)

A company wants to identify which of two production methods has the smaller completion time. One sample of workers is randomly selected and each worker first uses one method and then uses the other method. The sampling procedure being used to collect completion time data is based on _____ samples.
Answers
The sampling procedure being used to collect completion time data in this scenario is based on paired samples or dependent samples.
In paired samples, each observation in one sample is uniquely linked or paired with an observation in the other sample. In this case, the workers are randomly selected, and each worker is assigned to use both production methods, one after the other. The completion time for each worker is measured under both methods, creating paired or dependent observations.
By using paired samples, the company can compare the completion times of the same workers using different production methods. This approach helps eliminate individual differences and other sources of variability among workers, focusing solely on the comparison between the two methods.
To know more about samples,
https://brainly.com/question/15198199
#SPJ11
2
A cell phone tower is the
shape of a rectangular
pyramid. The base has
dimensions of 12 ft by 16 ft.
The tower takes up 1152 cubic
feet of space. How many feet
tall is the tower?
Answers
PLZZ HELP 50 POINTS!!!
How could you change the equation from Part B so it has infinitely many solutions? What would infinitely many solutions mean in terms of the situation?

Answers
Answer: To change the equation from Part B so it has infinitely many solutions, you could make the equation equal to itself 5x + 2 = 5x + 2
Step-by-step explanation:
5x + 2 = 5x + 2
5x + 2 - 5x = 5x + 2 - 5x
2 = 2
2 - 2 = 2 - 2
0 = 0
When a number is equal to itself, and it cancels out to 0 = 0, then the equation will have infinitely many solutions.
A grocery store sells a bag of 6 oranges for $4.80. If Austin spent $8.00 on oranges, how many did he buy
Answers
Answer:
10 oranges
Step-by-step explanation:
6 oranges is sold for $4.80
1 orange= 4.80/6
= $0.8
Austin spent $8.00 on oranges, then the amount of oranges he bought with this amount can be calculated as follows
= 8/0.8
= 10 oranges
what is the measure of angle NLP
55
90
Answers
Answer:
answer is 55° ..........
55 of the angle NLP
PLEASE HELP IT WORTH 50 points!!!!!

Answers
-3(-2)=6
-3+-2=-5
(X-3)(x-2)
Answer:
(x-3) (x-2)
Step-by-step explanation:
\(x^{2}\) - 5x + 6
How to break down the equation and factorise it:
-3 x -2 = 6
-3 + -2 = -5
Final Answer:
(x-3) (x-2)
I need the second one because i can't figure it out ;--;

Answers
Answer:
vertex form: y=a(x-h)^2+k ⇒ (a, h, k) = (-1/4, -2, 4)factored form: y=a(x+6)(x-2) ⇒ a = -1/4standard form: y=ax^2+bx+c ⇒ (a, b, c) = (-1/4, -1, 3)Step-by-step explanation:
We don't know how you did the first way, so the only way we can make sure another way is different is to do it two ways.
1) First, we'll make use of the vertex-form equation. The given zeros are at -6 and +2, so the line of symmetry is x = (-6+2)/2 = -2. Then vertex form of the equation will look like ...
y = a(x +2)^2 +k
We have two unknown values, so we need to make use of two points to find them.
Using (2, 0):
0 = a(2 +2)^2 +k
0 = 16a +k
Using (-4, 3):
3 = a(-4+2)^2 +k
3 = 4a +k
Subtracting the second equation from the first, we get
0 -3 = (16a +k) -(4a +k)
-3 = 12a
a = -1/4
Substituting into the first of our equations, ...
0 = 16(-1/4) + k = -4 +k
k = 4
So, the equation is ...
y = (-1/4)(x +2)^2 +4
__
2) Using factored form, we can write the equation as ...
y = a(x +6)(x -2) . . . . for zeros x=-6 and x=2
We can find 'a' by using the third point:
3 = a(-4+6)(-4-2) = a(2)(-6) = -12a
a = 3/-12 = -1/4
So, the equation is ...
y = (-1/4)(x +6)(x -2)
__
3) You can also make use of the standard form equation. This gives rise to three equations in the three coefficients.
y = ax^2 +bx +c
0 = a(-6)^2 +b(-6) +c = 36a -6b +c
3 = a(-4)^2 +b(-4) +c = 16a -4b +c
0 = a(2)^2 +b(2) +c = 4a +2b +c
These can be solved by your favorite method to give ...
a = -1/4, b = -1, c = 3
So, the equation is ...
y = (-1/4)x^2 -x +3
What is each sum or difference?
b. (1+5 i)-(3-2 i)
Answers
The sum or difference of (1+5i) and (3-2i) is: -2 + 7i
To find the sum or difference of (1+5i) and (3-2i), we simply combine the real and imaginary parts separately.
The real part is obtained by adding or subtracting the real parts of the complex numbers, and the imaginary part is obtained by adding or subtracting the imaginary parts.
Given:
(1 + 5i) - (3 - 2i)
For the real part:
1 - 3 = -2
For the imaginary part:
5i - (-2i) = 5i + 2i = 7i
Therefore, the sum or difference of (1+5i) and (3-2i) is:
-2 + 7i
learn more about difference here
https://brainly.com/question/30241588
#SPJ11
5x - 7 = 5 - x
Using balancing method in algebra
Answers
Answer:
5x-7-5+X=5-x-5+X
or,6x-12=0
or,6x=12
or,X=12/6
:.X=2
Or
X=12/6 and there is more ways but those are two ways
find two numbers whose difference is 164 and whose product is a minimum.
Answers
Answer: The lowest possible product would be -6724 given the numbers 82 and -82.
We can find this by setting the first number as x + 164. The other number would have to be simply x since it has to have a 164 difference.
Next we'll multiply the numbers together.
x(x+164)
x^2 + 164x
Now we want to minimize this as much as possible, so we'll find the vertex of this quadratic graph. You can do this by finding the x value as -b/2a, where b is the number attached to x and a is the number attached to x^2
-b/2a = -164/2(1) = -164/2 = -82
So we know one of the values is -82. We can plug that into the equation to find the second.
x + 164
-82 + 164
82
Step-by-step explanation: Hope this helps.
Find h(x, y) = g(f(x, y)).g(t) = t2 + sqrt(t), f(x, y) = 5x + 4y − 20Find the set on which h is continuous.
Answers
The set on which h is continuous is { (x, y) | 5x + 4y > 20 }. The function f(x, y) is a linear function and is defined for all values of x and y.
To determine the set on which h is continuous, we need to examine the domains of the functions f(x, y) and g(t), as well as the composition of these functions.
The function f(x, y) is a linear function and is defined for all values of x and y. The function g(t) is defined for all non-negative values of t (i.e., t ≥ 0), since it involves the square root of t.
The composition g(f(x, y)) is then defined for all (x, y) such that 5x + 4y - 20 ≥ 0, since f(x, y) must be non-negative for g(f(x, y)) to be defined. Simplifying this inequality, we get 5x + 4y > 20, which is the set on which g(f(x, y)) is defined.
Finally, the function h(x, y) = g(f(x, y)) is a composition of two continuous functions, and is therefore continuous on the set on which g(f(x, y)) is defined. Therefore, the set on which h is continuous is { (x, y) | 5x + 4y > 20 }.
Learn more about linear function here
https://brainly.com/question/2248255
#SPJ11
Mrs. Patel needs
7/8
yards of fabric to make one shirt. Mrs. Patel bought 10 1/2 image yards of fabric. How many shirts can she make?
Answers
Answer:
12 shirts
Step-by-step explanation:
I used the method keep, change, flip (KCF) to divide fractions and solve this problem.
This means Keep the first fraction, Change the division sign to a multiplication sign, and Flip the second fraction.
so keep 10 1/2, or 21/2, change sign, and flip the second fraction to 8/7.
that gives us the equation 21/2x8/7, and solving that gives us 168/14, or 168 divided by 14, so 12 shirts
if we have a class of 15 students and we want to choose a committee of 5 students, their order and position don't matter, how many different ways are there of creating a 5-person committee among the 15 students?
Answers
if we have a class of 15 students and we want to choose a committee of 5 students, their order and position don't matter, 3003 many different ways are there of creating a 5-person committee among the 15 students.
What is combination formula?The combination formula is used to determine how many options there are for choosing things from a collection so that the order in which they are chosen is irrelevant. Combination, to put it simply, is the choosing of items or things from a bigger group when the order doesn't important.
Since order and position doesn't matter in this problem, use the combination formula.
The combination formula is: n! / (n-r)! r!
where n is the total number of items (15 in this case) and r is the number of items being selected at once (5 in this case)
Plugging our numbers into the formula:
= 15! / (15-5)! 5!
= 3003 ways.
So, there are 3003 ways of picking 5 people from a group of 15.
To know more about combination formula refer to:
https://brainly.com/question/28065038
#SPJ4
Suppose a continuous random variable X is uniformly distributed on the interval [4,9]. able Y distributed? That is, determine the probability density function fy(y) 1. None of these. 2. for 4-y-9 = 10, 0 otherwise
Answers
For a continuous random variable X, which is uniformly distributed on an interval [4,9], the probability density function of \(f_Y( y)\) is equals to
\(f_Y( y) =\begin{cases} \frac{2y}{5},\quad 2≤ x ≤ 3 \\ 0, \quad \: otherwise\ \ \end{cases}\). So, option(5) is correct.
We have a continuous random variable X is uniformly distributed on the interval [4,9]. The PDF is a probability that a random variable acquire a value exactly same or equal to the random variable but in case of CDF, this probability values is less than or equal to the random variable. The probability density function for X is defined as \(f_X(x) = \frac{1}{b - a} \) so, we can write it as \(f_X ( x) =\begin{cases} \frac{1}{5},\quad 4≤ x ≤ 9 \\ 0, \quad otherwise \\ \end{cases}\).
We have to determine the probability density function \(f_Y(y)\). For this first we have to calculate the cumulative distribution function for f(x) is written as \(F_X(x) = \int_{4}^{x} f(x) dx \)
\(= \int_{4}^{x} \frac{1}{5} dx \)
\(= \frac{1}{5} [ x]_{4}^{x} \)
\(F_X(x) = \frac{x - 4}{5}\)
Now, we have, \( Y = \sqrt{X}\)
when X = 4 => Y = 2 and X = 9 => Y = 3
Also, X = Y²
Differentiating X = Y² with respect to Y
=> dX = 2Y dY
=> dX/dY = 2Y
Now, pdf of Y is written as \(f_Y(y) = f_X(x)|\frac{dX}{dY}| \)
\( = \frac{ 1}{5} × 2y\)
\(= \frac{ 2y}{5}\)
So, \(f_Y( y) =\begin{cases} \frac{2y}{5},\quad 2≤ x ≤ 3 \\ 0, \quad \: otherwise \ \ \end{cases}\). Hence, required value is \(f_Y( y) =\begin{cases} \frac{2y}{5},\quad 2≤ x ≤ 3 \\ 0, \quad \: otherwise \ \ \end{cases}\).
For more information about uniform distribution, visit :
https://brainly.com/question/31293679
#SPJ4
Complete question:
The above figure complete the question.
![Suppose a continuous random variable X is uniformly distributed on the interval [4,9]. able Y distributed?](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/nxh50RPDAVKvcQ3eaCbJnTUKucKYFdYM.jpeg)
A continuous random variable x is uniformly distributed on the interval [35, 45]. the probability that x is between 40 and 50 is:________
Answers
The probability that x is between 40 and 50 will be 0.5.
How to illustrate the probability?From the information, the continuous random variable x is uniformly distributed on the interval [35, 45].
The probability that x is between 40 and 50 will be:
(45 - 40)/(45 - 35)
= 5/10
= 0.5
Learn more about probability on:
brainly.com/question/24756209
#SPJ4
What’s 50.272 to 1 decimal place
Answers
TRUNCATED to one decimal place, it's 50.2
ROUNDED to one decimal place, it's 50.3
The round-off of 50.272 to 1 decimal place using rules of rounding
numbers are 50.3.
Rounding off numbers means making a number simpler by adjusting it to its nearest place according to certain rules.
Rounding a number to one decimal place means keeping only the first digit after the decimal point and neglecting the rest. In this case, the digit in the second decimal place is 7, which is greater than or equal to 5. As per the rounding rules, if the digit is greater than 5, the preceding digit is increased by 1.
So, 50.272 becomes 50.3 when rounded to one decimal place.
Learn more about rounding numbers here:
https://brainly.com/question/13391706
#SPJ4
HELP PLEASE! I don't understand this problem.
Answers
Answer:
So, you have to prove that Triangle ABC is congruent to Triangle ADC
&
it has been proved that they are congruent.
Step-by-step explanation:
We already know that Angle B is congruent to Angle D and AC bisects Angle BAD.
Because given rules one angle of one triangle is equal to the same side of the other.
Because of bisection, you also now know that Angle BAC is congruent to Angle CAD.
The sum of a triangle is 180 degrees.
Angle B and Angle BAC are equal to Angle D and Angle CAD.
180 degrees subtract from both of these if you knew the degrees would give the same answer.
This proves they are congruent.
Which is a correct solution for the following system of Inequalities
HELPP DUE IN 30MIN

Answers
Answer:
I think the answer is A
1,2
please help me I really need help

Answers
Answer:
Step-by-step explanation:
the volume of this prism is equal to
V=l*w*h
V=(x+1)(x)(x-3)
multiply
V=x^3-2x^2-3x
it is your first choice
Answer:
Step-by-step explanation:
\(V=LWH\\ \\ V=x(x+1)(x-3)\\ \\ V=x(x^2-2x-3)\\ \\ V=x^3-2x^2-3x\)