Determine whether each of these proposed definitions is a valid recursive definition of a function f from the set of nonnegative integers to the set of integers. If f is well defined, find a formula for f (n) when n is a nonnegative integer and prove that your formula is valid.
a) f (0) = 1, f (n) = −f (n − 1) for n ≥ 1
b) f (0) = 1, f (1) = 0, f (2) = 2, f (n) = 2f (n − 3)
Answers
a) This is a valid recursive definition of a function f from the set of nonnegative integers to the set of integers. The formula for f(n) is f(n) = f(n-1) for n ≥ 1. To prove that this formula is valid, we can use mathematical induction.
Base case: f(0) = 1, which is true.
Inductive step: Assume that f(k) = f(k-1) for some k ≥ 1. Then f(k+1) = f(k) = f(k-1) = f(k+1-1), which is true.
Therefore, the formula is valid.
b) This is a valid recursive definition of a function f from the set of nonnegative integers to the set of integers. The formula for f(n) is f(n) = 2f(n-3) for n ≥ 3. To prove that this formula is valid, we can use mathematical induction.
Base case: f(0) = 1, f(1) = 0, f(2) = 2, which are all true.
Inductive step: Assume that f(k) = 2f(k-3) for some k ≥ 3. Then f(k+1) = 2f(k+1-3) = 2f(k-2) = 2(2f(k-3)) = 2f(k), which is true.
Therefore, the formula is valid.
c) This is not a valid recursive definition of a function f from the set of nonnegative integers to the set of integers because the recursive step does not define f(n) for all n ≥ 0.
d) This is a valid recursive definition of a function f from the set of nonnegative integers to the set of integers. The formula for f(n) is f(n) = 2f(n-1) for n ≥ 1. To prove that this formula is valid, we can use mathematical induction.
Base case: f(0) = 0, f(1) = 1, which are both true.
Inductive step: Assume that f(k) = 2f(k-1) for some k ≥ 1. Then f(k+1) = 2f(k+1-1) = 2f(k) = 2(2f(k-1)) = 2f(k+1-1), which is true.
Therefore, the formula is valid.
e) This is a valid recursive definition of a function f from the set of nonnegative integers to the set of integers. The formula for f(n) is f(n) = f(n-1) if n is odd and n ≥1 and f(n) = 2f(n-2) if n≥ 2. To prove that this formula is valid, we can use mathematical induction.
Base case: f(0) = 2, which is true.
Inductive step: Assume that f(k) = f(k-1) if k is odd and k ≥ 1 and f(k) = 2f(k-2) if k ≥ 2.
If k is odd, then f(k+1) = f(k) = f(k-1) = f(k+1-1), which is true.
If k is even, then f(k+1) = 2f(k+1-2) = 2f(k) = 2(2f(k-2)) = 2f(k+1-2), which is true.
Therefore, the formula is valid.
a) The formula for f(n) is (-1)ⁿ and b) The formula for f(n) is f(n) = 2k.
a) The proposed definition of function f is a valid recursive definition as it defines f(0) as 1 and then uses the previous value of f(n-1) to determine the value of f(n) for all n greater than or equal to 1. To find the formula for f(n), we can use induction. We can see that f(1) = -f(0) = -1, f(2) = -f(1) = 1, f(3) = -f(2) = -1, and so on. Thus, we can see that f(n) alternates between 1 and -1, depending on whether n is odd or even. Therefore, the formula for f(n) is (-1)ⁿ.
b) The proposed definition of function f is also a valid recursive definition as it defines f(0), f(1), and f(2), and then uses the previous value of f(n-3) to determine the value of f(n) for all n greater than or equal to 3. To find the formula for f(n), we can again use induction. We can see that f(3) = 2f(0) = 2, f(4) = 2f(1) = 0, f(5) = 2f(2) = 4, f(6) = 2f(3) = 4, f(7) = 2f(4) = 0, and so on.
Thus, we can see that f(n) alternates between 0 and 2, depending on whether n is congruent to 1 or 2 mod 3. Therefore, the formula for f(n) is f(n) = 2k, where k is the number of times n-3 can be divided by 3 before reaching a number less than or equal to 2. This formula is valid as it agrees with our observations and satisfies the recursive definition.
For more about formula:
https://brainly.com/question/30098455
#SPJ4
Related Questions
it is known that the population variance equals 522. what is the sample size that needs to be taken if the desired margin of error is 4 or less with 0.95 probability?
Answers
If the intended margin of error equals 4 less than with a 0.95 probability, the sample size is 126.
The \(\alpha\) level is calculated by subtracting 1 from the confidence interval and dividing by 2.
\(\alpha\) = (1 - 0.95) ÷ 2
\(\alpha\) = 0.025
Find z inside the Z-table because it has a p-value of 1 - \(\alpha\).
So, z = 1.96 with a p-value = 1 - 0.025 = 0.975.
Now, consider that margin of error M.
M = z × (σ ÷ √n)
The standard deviation is determined as the square root of variance.
σ = √522 = 22.84
With a 0.95 probability, the sample size that requires to be accepted if the expected margin of error is 4 or less is,
The sample size of at least n, in which n is encountered when M = 4. So,
M = z × (σ ÷ √n)
4 = 1.96 × (22.84 ÷ √n)
4√n = 1.96 × 22.84
√n = (1.96 × 22.84) ÷ 4
√n = 11.1916
n = (11.1916)²
n = 125.25 ≈ 126
A sample size of at minimum 126 people is required.
Learn more about the probability at
https://brainly.com/question/15121653?referrer=searchResults
#SPJ4
Find the slope for the line that passes through the points (-2,5) and (1,0)
Answers
Answer:
\(m=\frac{-5}{3}\)
Step-by-step explanation:
Pre-SolvingWe want to find the slope between the points (-2,5) and (1,0).
The slope (m) can be found using the formula \(\frac{y_2-y_1}{x_2-x_1}\), where \((x_1,y_1)\) and \((x_2,y_2)\) are points.
SolvingWe are already given the values of the points, but let's label their values to avoid any confusion and mistakes.
\(x_1=-2\\y_1=5\\x_2=1\\y_2=0\)
Now, substitute into the formula.
\(m=\frac{y_2-y_1}{x_2-x_1}\)
\(m=\frac{0-5}{1--2}\)
Simplify this to:
\(m=\frac{0-5}{1+2}\)
\(m=\frac{-5}{3}\)
The slope is -5/3.
To convert 120 ounces to pounds, which of the following proportions should you use?
ANSWER VERY QUICKLY PLEASE!!!! NEED ANSWERS ASAP.
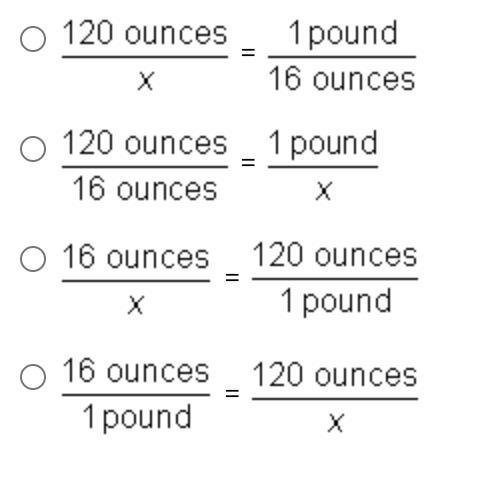
Answers
Answer: you would use the last option
Angel bought 2 books at Rs. 500 each. He sold one of them at 25% profit and the other at 25% loss. Then, find the total profit or loss percent for him.
Answers
Answer And Explanation


Answer:
He neither earn profit nor gain loss
Step-by-step explanation:
Because he gain profit of 25 % by selling at price of 625 and gain loss of 25 % by selling second book at price of 375.
So if you add these profit and loss
625 +375 = 1000
1000 which is his actual money
HELP ASAP!!!!!! AND NO LINKS!!! The Utah Bees discounts tickets 30% for students 14 or younger. If adult tickets cost $23, how much will a student ticket cost after being discounted? Round to the nearest cent if necessary.
Answers
Answer:
$6.90
Step-by-step explanation:
30/100 = x/23
100x = 690
x= $6.90
Write a system of equations to describe the situation below, solve using any method, and fill in the blanks. Norma is a salon owner. Yesterday, she did 1 haircut and colored the hair of 2 clients, charging a total of $217. Today, she did 2 haircuts and colored the hair of 1 client, charging a total of $155. How much does Norma charge for her services? PLEASE ANSWER
Answers
Answer:
Cost of haircut = $93
Cost of colouring hair = $31
Step-by-step explanation:
Let
Cost of haircut = x
Cost of colouring hair = y
The equations
x + 2y = 217 (1)
2x + y = 155 (2)
From (1)
x = 217 - 2y
Substitute x = 217 - 2y into (2)
2x + y = 155
2(217 - 2y) + y = 155
434 - 4y + y = 155
-3y = 155 - 434
-3y = -279
y = -279 / -3
= 93
y = $93
Substitute y = 93 into (1)
x + 2y = 217
x + 2(93) = 217
x + 186 = 217
x = 217 - 186
= 31
x = $31
Cost of haircut = $93
Cost of colouring hair = $31
Using f(x) = -5x + 12, evaluate f (-2)
Answers
Answer:
22Step-by-step explanation:
f(-2) means that the "x" variable in the equation can be substituted for -2
So, we have
-5(-2) + 12
This equals 10 + 12 = 22
So, the answer is 22
please someone help me asap i will give brainliest to correct answer!

Answers
Answer:
C
Step-by-step explanation:
it's c because this is a false statement, which means that the original statement is also a false one
so it doesn't have any answer
Given the function y=-\frac{3\sqrt{x^5}}{4},y=− 4 3 x 5 , find \frac{dy}{dx}. dx dy . Express your answer in radical form without using negative exponents, simplifying all fractions.
Answers
Given:
The function is:
\(y=-\dfrac{3\sqrt{x^5}}{4}\)
To find:
The value of \(\dfrac{dy}{dx}\).
Solution:
We have,
\(y=-\dfrac{3\sqrt{x^5}}{4}\)
It can be written as
\(y=-\dfrac{3}{4}x^{\frac{5}{2}}\) \([\because \sqrt[n]x=x^\frac{1}{n}]\)
Differentiate with respect to x.
\(\dfrac{dy}{dx}=-\dfrac{3}{4}\times \dfrac{5}{2}x^{\frac{5}{2}-1}\) \([\because \dfrac{d}{dx}x^n=nx^{n-1}]\)
\(\dfrac{dy}{dx}=-\dfrac{15}{8}x^{\frac{5-2}{2}}\)
\(\dfrac{dy}{dx}=-\dfrac{15}{8}x^{\frac{3}{2}}\)
\(\dfrac{dy}{dx}=-\dfrac{15}{8}\sqrt{x^3}\)
Therefore, the value of \(\dfrac{dy}{dx}\) is \(-\dfrac{15}{8}\sqrt{x^3}\).
Simplify the expression.
5+6(2x-3) - 4x
A. 8x-13
B. 8x+2
C. -18x-23
D. -18x-8
Answers
The Answer is A. 8x-13
Step-by-step explanation:
Trust
nate has a grid made of shaded and unshaded 2 cm by 2 cm squares, as shown. he randomly places a circle with a diameter of 3 cm on the board so that the centre of the circle is at the meeting point of four squares. the probability that he places the disk so that it is touching an equal number of shaded and unshaded squares is ab. what is a b ?
Answers
The value of a and b is 1.
THE PROBABILITY OF A AND BThe probability that Nate places the disk so that it is touching an equal number of shaded and unshaded squares is ab, where a and b are integers.
To find the value of a and b, we need to determine the total number of ways Nate can place the disk (the denominator of the probability fraction) and the number of ways he can place the disk so that it touches an equal number of shaded and unshaded squares (the numerator of the probability fraction).
Since the center of the circle must be at the meeting point of four squares, the only possible places for the center are the points where four squares meet. Since the grid is made of 2 cm x 2 cm squares, there are 4 shaded squares and 4 unshaded squares. So, there are 4 centers that could be placed on a shaded square and 4 centers that could be placed on an unshaded square.
So the denominator of the probability fraction is 8.
Now, to calculate the numerator, we need to determine the number of ways Nate can place the disk so that it touches an equal number of shaded and unshaded squares.
As the center of the circle is at the meeting point of four squares, the center of the circle is placed at the intersection of 2 shaded and 2 unshaded squares.
So, the numerator of the probability fraction is 8.
Therefore, the probability that Nate places the disk so that it is touching an equal number of shaded and unshaded squares is 8 ÷ 8 =1.
So the value of a and b is 1.
Learn more about Probability here:
https://brainly.com/question/11234923
#SPJ4
PLEASE HELP ITS DISTRIBUTIVE PROPERTY HELPPPPPPPPPPPPPPPPPPPPPPP EXPLAIN YOUR ANSWER PLEASEEE
Answers
Hello! Please see the picture to see the question, Thank you!

Answers
7)
The given function is
\(f(x)=2x^2+4x^3+3x+5\)Recall that the degree of the polynomial is the highest power of the variable.
The degree of the given polynomial function is 3.
we know that a cubic function is a polynomial function with degree 3.
Hence the given function is a cubic function.
Option D is correct.
Which statement(s) is/are correct about the t distribution?.......A. Mean = 0 B. Symmetric C. Based on degrees of freedom D. All of these are correct
Answers
D. All of these are correct.
The t-distribution has the following characteristics:
A. The mean of the t-distribution is indeed 0. This means that the expected value of a t-distributed random variable is 0.
B. The t-distribution is symmetric around the mean of 0. This means that the probability density function (PDF) of the t-distribution is symmetric and has equal probabilities of positive and negative values.
C. The t-distribution is based on degrees of freedom. The shape of the t-distribution depends on the degrees of freedom (df) parameter, which determines the number of independent observations used to estimate a population parameter. As the degrees of freedom increase, the t-distribution approaches the standard normal distribution.
all of the statements A, B, and C are correct about the t-distribution.
to know more about t-distribution visit:
brainly.com/question/15776502
#SPJ11
What is the area of the square
One side has 5 feet
A)10 square feet
B) 25 square feet
C) 20 square feet
D) 5 square feet
Answers
URGENT PLEASE I NEED IT RN!! THANKS
8. Prove the triangles are congruent

Answers
Step-by-step explanation:
Angle BAD = Angle CDA (Alternative angle)
AD=AD (Common side)
AB=CD (Given)
Thus, the given triangles are congruent by SAS.
(5.04×10^12)÷(6.3×10^9) in scientific notation
Answers
Answer:
i think the answer will be = 8 × 10^2
=0.8*10^3
Let the long-run profit function for a representative firm is given by π i
=p 2
−2p−399, where p is the price of computer. The inverse market demand for computer is given by p=39−0.009q, where q is unit of computers. Suppose technology for producing computers is identical for all firms and all firms face identical input prices. (a) Find the firm's output supply function. (b) Find the market-equilibrium price and the equilibrium number of firms. (c) Find the number of computers sold by each firm in the long run.
Answers
(a) The firm's output supply function is given by q = (p + 199) / 2.
(b) The market-equilibrium price is $32.56, and the equilibrium number of firms is 10.
(c) Each firm sells 70 computers in the long run.
To find the firm's output supply function, we need to maximize the firm's profit function, which is given by π = p^2 - 2p - 399. In the long run, firms will produce where marginal cost equals marginal revenue. Marginal revenue can be obtained by differentiating the inverse market demand function with respect to q, and marginal cost is equal to the derivative of the profit function with respect to q. Equating the two, we get:(39 - 0.009q) = (2q - 2) / q
Simplifying the equation, we find:
q = (p + 199) / 2
This represents the firm's output supply function.
To find the market-equilibrium price and the equilibrium number of firms, we need to find the intersection point of the market demand and supply. Substituting the output supply function into the inverse market demand function, we have:p = 39 - 0.009((p + 199) / 2)
Simplifying and solving for p, we get:
p ≈ $32.56
Substituting this price back into the output supply function, we find:
q = (32.56 + 199) / 2 ≈ 115.78
Given that each firm produces 70 computers in the long run, we can calculate the equilibrium number of firms:
Number of firms = q / 70 ≈ 10
Since each firm sells 70 computers in the long run, and there are 10 firms, the total number of computers sold by each firm is:70 * 10 = 700
Learn more about Equilibrium
brainly.com/question/30694482
#SPJ11
36. Mrs. Moore bought one gallon of milk at
$3 per gallon, three loaves of bread at
$2 per loaf, one pound of cheese at $4 per
pound, and six cans of soup at two cans for
$3. What was the total cost of the food?
Answers
Do u know this? Answer if u do

Answers
Answer:
Hi
Step-by-step explanation:
The expression was reduced to it's lowest expression or term or we say we found the common factor amongst them
III Homework: Homework 2 < > Save Part 1 of 2 O Points: 0 of 1 The parametric equations and parameter intervals for the motion of a particle in the xy-plane are given below. Identify the particle's path by finding a Cartesian equation for it. Graph the Cartesian equation. Indicate the portion of the graph traced by the particle and the direction of motion. x= cos (21), y= sin (21), Osts 2.
Answers
The graph of the Cartesian equation x² + y² = 1 is attached in the image.
What is the trigonometric ratio?
the trigonometric functions are real functions that relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others.
The parametric equations for the motion of the particle in the xy-plane are:
x = cos(t)
y = sin(t)
To find the Cartesian equation, we can eliminate the parameter t by squaring both equations and adding them together:
x² + y² = cos²(t) + sin²(t)
Using the trigonometric identity cos²(t) + sin²(t) = 1, we have:
x² + y² = 1
This is the equation of a circle with radius 1 centered at the origin (0,0) in the Cartesian coordinate system.
The graph of the Cartesian equation x² + y² = 1 is a circle with radius of 1. The portion of the graph traced by the particle corresponds to the circle itself.
Since the equations x = cos(t) and y = sin(t) represent the particle's motion in a counterclockwise direction, the particle moves along the circle in the counterclockwise direction.
Hence, the graph of the Cartesian equation x² + y² = 1 is attached in the image.
To learn more about the trigonometric ratio visit:
https://brainly.com/question/13729598
#SPJ4

CC has the following beginning balances in its stockholders' equity accounts on January 1, 2012: Common Stock, $100,000; Additional Paid-in Capital, $4,100,000; and Retained Earnings, $3,000,000. Net income for the year ended December 31, 2012, is $800,000. Court Casuals has the following transactions affecting stockholders' equity in 2012:
May 18 Issues 25,000 additional shares of $1 par value common stock for $40 per share.
May 31 Repurchases 5,000 shares of treasury stock for $45 per share.
July 1 Declares a cash dividend of $1 per share to all stockholders of record on July 15. Hint: Dividends are not paid on treasury stock.
July 31 Pays the cash dividend declared on July 1.
August 10 Reissues 2,500 shares of treasury stock purchased on May 31 for $48 per share.
Taking into consideration all the entries described above, prepare the statement of stockholders' equity for the year ended December 31, 2012.
Answers
Total stockholders’ equity 7,800,000
Statement of stockholders’ equity for CC for the year ended December 31, 2012:Particulars Amount ($)
Common Stock 100,000
Additional Paid-in Capital 4,100,000
Retained Earnings (Opening Balance) 3,000,000
Add: Net Income for the year ended December 31, 2012 800,000
Total retained earnings 3,800,000
Less: Cash Dividend Declared on July 1 and paid on July 31 (200,000)
Retained earnings (Closing balance) 3,600,000
Total stockholders’ equity 7,800,000
Explanation:The given information is as follows:Common Stock on January 1, 2012 = $100,000Additional Paid-in Capital on January 1, 2012 = $4,100,000
Retained Earnings on January 1, 2012 = $3,000,000Net Income for the year ended December 31, 2012 = $800,000Cash Dividend Declared on July 1 and paid on July 31 = $200,000
To prepare the statement of stockholders’ equity for the year ended December 31, 2012, we will begin by preparing the opening balances of each of the equity accounts. We will then add the net income to the retained earnings account.
The closing balance for retained earnings is then computed by subtracting the cash dividend declared and paid from the total retained earnings. Finally, the total stockholders' equity is calculated by adding the balances of all the equity accounts.
Calculations:Opening balance of common stock = $100,000
Opening balance of additional paid-in capital = $4,100,000
Opening balance of retained earnings = $3,000,000
Net Income for the year ended December 31, 2012 = $800,000
Retained earnings (Opening Balance) = $3,000,000
Add: Net Income for the year ended December 31, 2012 = $800,000
Total retained earnings = $3,800,000Less: Cash Dividend Declared on July 1 and paid on July 31 = $200,000Retained earnings (Closing balance) = $3,600,000
Total stockholders’ equity = Common Stock + Additional Paid-in Capital + Retained Earnings (Closing balance) = $100,000 + $4,100,000 + $3,600,000 = $7,800,000
Therefore, the statement of stockholders’ equity for CC for the year ended December 31, 2012, is as follows:Particulars Amount ($)
Common Stock 100,000
Additional Paid-in Capital 4,100,000
Retained Earnings (Opening Balance) 3,000,000
Add: Net Income for the year ended December 31, 2012 800,000
Total retained earnings 3,800,000
Less: Cash Dividend Declared on July 1 and paid on July 31 (200,000)
Retained earnings (Closing balance) 3,600,000
To learn more about : equity
https://brainly.com/question/27821130
#SPJ8
Calculate the (modeled) probability P(E) using the given information, assuming that all outcomes are equally likely.
S = {1, 3, 5, 7, 9}, E = {1, 5, 7}
Answers
The probability P(E) is 13/15.
According to the statement
we have given that the S = {1, 3, 5, 7, 9}, E = {1, 5, 7}
And we have to find the probability P(E).
So, For this purpose
Recall the formula for the probability of an event E in case when all outcomes are equally likely:
P(E)= n(E) /n(S)
in which S is the sample space.
But we have the S = {1, 3, 5, 7, 9},
so, n(S) = Sum of all outcomes / number of outcomes
n(S) = 1+3+5+7+9 /5
n(S) = 25 /5
n(S) = 5 and
For n(E) = Sum of all outcomes / number of outcomes
n(E) = 1+5+7 /3
n(E) = 13 /3
n(E) = 13 /3
Substitute these values in the above written formula then
P(E)= n(E) /n(S)
P(E)= (13/3)/ 5
P(E)= 13 /15
So, The probability P(E) is 13/15.
Learn more about the PROBABILITY here https://brainly.com/question/25870256
#SPJ4
Brian loves to bake blueberry muffins for his friends and family.
there is a proportional relationship between the volume of flour brian uses (in cups), x, and
the number of muffins he bakes, y.
10
9
8
7
9
s
s
3
2
2
s
9
00
9
10
Answers
For a proportional relationship between the volume of flour used (in cups), x, and the number of baked muffins, y, the constant of proportionality is 4.
Constant of proportionality, also known as constant ratio or constant rate, refers to is the ratio that relates two given values in a data set that is represented as a proportional relationship. When two parameters are proportional, either directly or indirectly, the relationship is expressed as a = kb or a = k/b, where k indicates the relationship between the two variables and is known as the proportionality constant. In the given data, the proportionality constant is:
k =b/a = 8/2 =12/3 = 16/4 = 20/4 = 4
Hence, the proportionality constant for the given data is 4.
Notes: The question is incomplete. The complete question is: Brian loves to bake blueberry muffins for his friends and family. There is a proportional relationship between the volume of flour brian uses (in cups), x, and the number of muffins he bakes, y. What is the constant of proportionality. (Refer to the table).
Learn more about Constant of proportionality:
https://brainly.com/question/28413384
#SPJ4

let r be the relation on the set of ordered pairs of positive integers such that ((a, b), (c, d)) ∈ r if and only if ad
Answers
The relation "r" on the set of ordered pairs of positive integers is defined as follows: ((a, b), (c, d)) ∈ r if and only if ad < bc.
In simpler terms, for any two ordered pairs of positive integers (a, b) and (c, d), they are related if and only if the product of the first integer in the first pair and the second integer in the second pair is less than the product of the second integer in the first pair and the first integer in the second pair.
Let's go through an example to better understand this concept. Consider the ordered pairs (2, 5) and (3, 4). To determine if they are related according to the relation "r," we need to compare the products: 2 * 4 = 8 and 5 * 3 = 15. Since 8 is less than 15, we can conclude that ((2, 5), (3, 4)) ∈ r.
It's important to note that the relation "r" compares the products of the integers in the ordered pairs, rather than the integers themselves. The relation checks if the product of the first integer in the first pair and the second integer in the second pair is less than the product of the second integer in the first pair and the first integer in the second pair.
I hope this explanation clarifies the meaning of the relation "r" on the set of ordered pairs of positive integers. If you have any further questions, feel free to ask!
relation and positive integers : https://brainly.com/question/28165413
#SPJ11
Hi I don’t have a protractor right now and I reallyyy need help answering these questions I don’t understand or I’ll get a 0. Can anyone help me please?
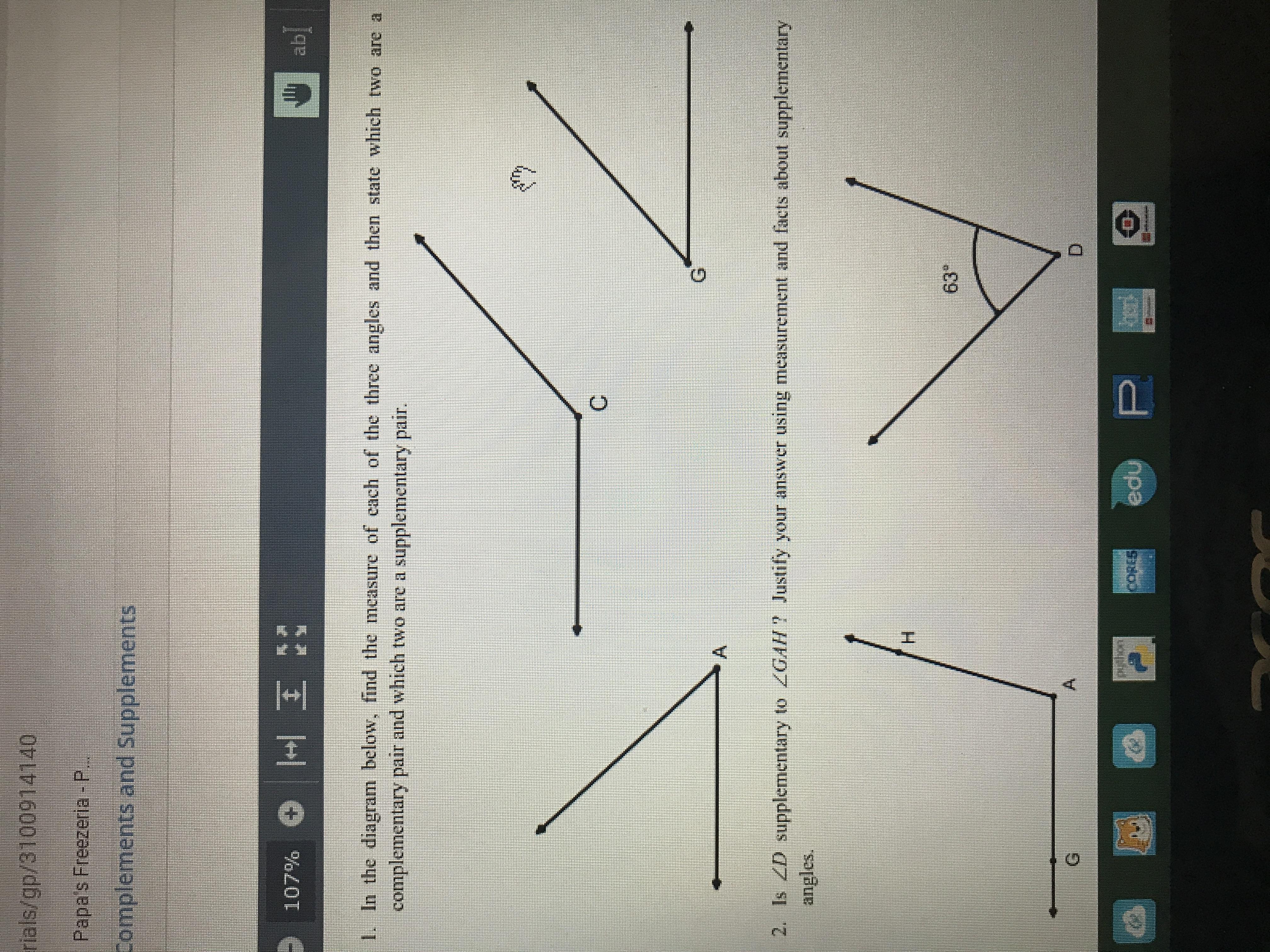
Answers
Answer:
hhrnfg
Step-by-step explanation:
jsfd
Is it non proportional or proportional

Answers
Answer:
proportional I think
Step-by-step explanation:
if it goes straight through the zero it is proportional.
can 133.97 be an answer to a cone with a radius of 4 inches and a height of 8 inches
Answers
Answer:
no
Step-by-step explanation:
the answer is 134.04
A store is having a sale on walnuts and chocolate chips. For 12 pounds of walnuts and 2 pounds of chocolate chips, the total cost is $45. For 3 pounds of walnuts and 5 pounds of chocolate chips, the total cost is $18. Find the cost for each pound of walnuts and each pound of chocolate chips.
cost for each pound of walnuts:
cost for each pound of chocolate chips:
Answers
Answer:
Each pound of walnuts cost $3.50 and each pound of chocolate chips cost $1.50
Step-by-step explanation:
Let the cost of one pound of walnuts = $w
and the cost of one pound of chocolate chips = $c
Cost of 12 pounds of walnuts and 2 pounds of chocolate chips = $45
12w + 2c = 45 ------(1)
Cost of 3 pounds of walnuts and 5 pounds of chocolate chips = $18
3w + 5c = 18 --------(2)
Multiply equation (2) by 4 then subtract it from equation (1)
(12w + 2c) - (12w + 20c) = 45 - 72
-18c = -27
c = \(\frac{27}{18}\)
c = $1.5
Substitute c = 1.5 in equation (1),
12w + 2(1.5) = 45
12w = 45 - 3
w = \(\frac{42}{12}\)
w = $3.5
Therefore, each pound of walnuts cost $3.5 and each pound of chocolate chips cost $1.5
3-4/5X-2/3–3/15+3/5divided by -3/2
Answers
Answer:
-2(6x-13)/15
Step-by-step explanation:
This is done by simplifying the expression as well as combining like terms