Find the first three terms of Taylor series for F(x) = Sin(pnx) + e*-, about x = p, and use it to approximate F(2p)
Answers
The Taylor series for a function f(x) about a point a can be represented as: f(x) = f(a) + f'(a)(x - a)/1! + f''(a)(x - a)²/2! + f'''(a)(x - a)³/3! + ...
For the given function F(x) = Sin(pnx) + e*-, we want to find the first three terms of its Taylor series about x = p, and then use it to approximate F(2p).
To find the first three terms, we need to calculate the function's derivatives at x = p:
F(p) = Sin(pnp) + e*- = Sin(p^2n) + e*-
F'(p) = (d/dx)[Sin(pnx) + e*-] = npCos(pnp)
F''(p) = (d²/dx²)[Sin(pnx) + e*-] = -n²p²Sin(pnp)
Substituting these values into the Taylor series formula, we have:
F(x) ≈ F(p) + F'(p)(x - p)/1! + F''(p)(x - p)²/2!
Approximating F(2p) using this Taylor series expansion:
F(2p) ≈ F(p) + F'(p)(2p - p)/1! + F''(p)(2p - p)²/2!
Simplifying this expression will give an approximation for F(2p) using the first three terms of the Taylor series.
For more information on taylor series visit: brainly.com/question/31585708
#SPJ11
Related Questions
Class A has 20 students, Class B has 15 students, if the average weight of the students of 2 classes is 34.2 kg and the ratio of the total weight of the students of class A to that of class B is 11:8, find the average weight of the students of class A
Answers
Answer:
the average weight of the students in Class A is 25.92 kg.
the resultant data are: forty mothers have taken the suspected drug during their pregnancies. of these mothers, 35 have delivered malformed infants. in addition, 10 other infants are born with malfunctions. what type of study design is this?
Answers
The study is investigating the relationship between the exposure to the suspected drug during pregnancy and the risk
of delivering a malformed infant. This study design is a case-control study design.
The resultant data are: forty mothers have taken the suspected drug during their pregnancies. Of these mothers, 35
have delivered malformed infants. In addition, 10 other infants are born with malfunctions," then the answer would be
as follows:
The type of study design that is described in this scenario is a case-control study design.
A case-control study design is a type of observational study design that compares people with a particular condition
(cases) to people without that condition (controls) to determine whether there is a relationship between the exposure
to a suspected risk factor and the development of the condition.
In this scenario, the cases are the 35 mothers who delivered malformed infants, and the controls are the 5 mothers
who did not deliver malformed infants. The study is investigating the relationship between the exposure to the
suspected drug during pregnancy and the risk of delivering a malformed infant. Therefore, this study design is a case
control study design.
for such more question on case-control
https://brainly.com/question/735261
#SPJ11
Which equation can be represented using the number line?
A number line going from to 1 in increments of one-eighths. Arrows go from each mark on the line to the next up to three-fourths.
Three-fourths divided by one-eighth = 6
One-eighth divided by three-fourths = 6
6 divided by three-fourths = one-eighth
6 divided by one-eighth = three-fourths

Answers
Answer:
a
Step-by-step explanation:
The equation which can be represented using the picture displayed on the number line is Three-fourths divided by one-eighth = 6
The distance between each marked line on the number line is 1/8The length of the number line is 3/4The number of steps or marked points can be obtained using the relation :
Length of line ÷ Distance between each marked points
3/4 ÷ 1/8 = 6
Therefore, the expression which represents the scenario on the number line is 3/4 ÷ 1/8 = 6
Learn more :https://brainly.com/question/18112348
A linear equation determines a line in the xy-plane.A. TrueB. False
Answers
The correct answer is A. True
A linear equation represents a line in the xy-plane. In the form of y = mx + b, where m is the slope and b is the y-intercept, a linear equation defines a straight line relationship between x and y. Each x value corresponds to a unique y value on the line.
By plotting the points that satisfy the equation, a line can be formed. The slope determines the steepness or direction of the line, while the y-intercept represents the point where the line intersects the y-axis.
Therefore, a linear equation does determine a line in the xy-plane.
Learn more about linear equation here
https://brainly.com/question/32634451
#SPJ4
True. A linear equation determines a line in the xy-plane.
A linear equation is an equation that describes a straight line in the xy-plane. It is an equation of the form y = mx + b, where m represents the slope of the line and b represents the y-intercept. The slope-intercept form of a linear equation is commonly used to graph lines.
The equation y = mx + b shows that for every value of x, there is a corresponding value of y that lies on the line. The slope, m, determines the steepness of the line, while the y-intercept, b, represents the point where the line crosses the y-axis.
Therefore, it is true that a linear equation determines a line in the xy-plane.
Learn more:About linear equation here:
https://brainly.com/question/32634451
#SPJ11
i really need help please answer this

Answers
Answer:
Option 1
Step-by-step explanation:
Solve each piece individually first.
4 ^(1/2) = 2
The 4th root of 16 is 2 so 2/2 = 1
So we have:
2 * 1 - 10 ÷ 2
Order of operations.
2 * 1 = 2 10 ÷ 2 = 5
2 - 5 = -3
The answer is the first option.
(b) Given the matrix D = k 0 0 3 k² k³ 0 kª k³ kº k k k 0 0 0 k¹⁰ Find all possible value(s) of k if det(D) = 1024."
Answers
To find the possible values of k, we need to calculate the determinant of matrix D and set it equal to 1024.
Given matrix D:
D = | k 0 0 |
| 3 k² k³ |
| 0 kª k³ kº |
| k k k |
| 0 0 0 |
| k¹⁰ |
The determinant of D can be calculated by expanding along the first row or the first column. Let's expand along the first row:
det(D) = k(det | k³ k k |
| 0 k³ kº |
| 0 0 k¹⁰ |)
- 0(det | 3 k² k³ |
| 0 kª k³ |
| k k k |)
+ 0(det | 3 k² k³ |
| k k k |
| k k k |)
Simplifying further, we have:
det(D) = k(det | k³ k k |
| 0 k³ kº |
| 0 0 k¹⁰ |)
Now, we can calculate the determinant of the 3x3 submatrix:
det | k³ k k |
| 0 k³ kº |
| 0 0 k¹⁰ |
This determinant can be found by expanding along the first row or the first column. Expanding along the first row gives us:
det = k(k³(kº) - 0(k)) - 0(0(k¹⁰)) = k⁴kº = k⁴+kº
Now, we can set det(D) equal to 1024 and solve for k:
k⁴+kº = 1024
Since we are looking for all possible values of k, we need to solve this equation for k. However, solving this equation may require numerical methods or approximations, as it is a quartic equation.
Learn more about matrix here
https://brainly.com/question/2456804
#SPJ11
(1 point) for the system of differential equations x′(t)=−95x 53y 2xy y′(t)=−185x 203y−xy
Answers
The given system of differential equations is:
x'(t) = -95x + 53y - 2xy
y'(t) = -185x - 203y - xy
To solve this system, we can use various methods such as substitution or matrix methods. Let's solve it using the matrix method.
We can rewrite the system of differential equations in matrix form as:
X' = AX
where X = [x y]', X' = [x'(t) y'(t)]', and A is the coefficient matrix:
A = [[-95 53], [-185 -203]]
To find the solutions, we need to find the eigenvalues and eigenvectors of matrix A. The eigenvalues are the roots of the characteristic equation det(A - λI) = 0, where I is the identity matrix. Solving this equation gives us the eigenvalues λ1 = -100 and λ2 = -198.
Next, we find the eigenvectors associated with each eigenvalue. For λ1 = -100, the corresponding eigenvector is [2 1]'. For λ2 = -198, the corresponding eigenvector is [-1 1]'.
Therefore, the general solution of the system of differential equations is:
X(t) = c1e^(-100t)[2 1]' + c2e^(-198t)[-1 1]'
where c1 and c2 are constants determined by initial conditions.
In summary, the solution to the system of differential equations is given by X(t) = c1e^(-100t)[2 1]' + c2e^(-198t)[-1 1]', where c1 and c2 are constants determined by the initial conditions.
Learn more about matrix method here: brainly.com/question/31504272
#SPJ11
If a family has five girls and plans to have another child, answer the following if the probability of the event of a boy being born is \( \frac{1}{2} \), and births are independent events. a. What is
Answers
In a family with five girls and the probability of a boy being born is 1/2, the probability of the next child being a boy is still 1/2.
The previous births do not affect the probability of the next birth since each birth is an independent event.
The probability of an event occurring is determined by the ratio of the number of favorable outcomes to the total number of possible outcomes. In this case, the event of interest is the birth of a boy.
Since each birth is an independent event, the probability of having a boy on any given birth is always 1/2, regardless of the previous children born.
In the given scenario, the family already has five girls. This information is not relevant to the probability of the next child being a boy. The gender of the previous children does not affect the probability of the next child being a boy or a girl.
Therefore, the probability of the next child being a boy remains 1/2, as it is for any independent birth event.
To learn more about independent event visit:
brainly.com/question/32716243
#SPJ11
The five values for a data set are: minimum = 0 lower quartile = 2 median = 3. 5 upper quartile = 5 maximum = 10 Bruno created the box plot using the five values. What error did he make? The right whisker should go from 3. 5 to 10. The left whisker should go from 0 to 2. The box should go from 2 to 3. 5. The box should go from 3. 5 to 5
Answers
The five values for a data set are: minimum = 0 lower quartile = 2 median = 3. 5 upper quartile = 5 maximum = 10 Bruno created the box plot using the five values. Bruno made error. The left whisker should go from 0 to 2.
About quartileQuartiles is a type of quartile that divides data into four parts with approximately the same number. The first quartile or lower quartile (Q1) is the middle value between the smallest value and the median of the data group. The first quartile is a marker that the data in that quartile is 25% below the data group.
The second quartile (Q2) is the median data which marks 50% of the data (dividing the data in half). The third or upper quartile (Q3) is the middle value between the median and the highest value of the data set. The third quartile is a marker that the data in that quartile is 75% below the data group. Quartiles are a form of an ordered statistic because to determine quartiles, data needs to be sorted from smallest to largest value first.
Learn more about quartile at https://brainly.com/question/24329548.
#SPJ4
A company is thinking about offering employee wellness classes during operational hours to boost production. They want to perform an experiment to see if employees attending these classes improve their quality of work. What is the best way to randomly choose a group of employees to attend these classes?
Answers
Answer:
Use a computer software program that will pick employees randomly from a list.
Answer:
Use a computer software program that will pick employees randomly from a list
Step-by-step explanation
i took the test :)
Using integration by parts, rewrite the following integral as fudv = uv-fvdu [in (2x) e 4x² dx
Answers
To rewrite the integral ∫(2x)\(e^{4x^{2} }\)dx using integration by parts, we'll consider the function f(x) = (2x) and g'(x) = \(e^{4x^{2} }\).
Integration by parts states that ∫u dv = uv - ∫v du, where u and v are functions of x.
Let's assign:
u = (2x) => du = 2 dx
dv = \(e^{4x^{2} }\) dx => v = ∫\(e^{4x^{2} }\) dx
To evaluate the integral of v, we need to use a technique called the error function (erf). The integral cannot be expressed in terms of elementary functions. Hence, we'll express the integral as follows:
∫\(e^{4x^{2} }\) dx = √(π/4) × erf(2x)
Now, we can rewrite the integral using integration by parts:
∫(2x)\(e^{4x^{2} }\) dx = uv - ∫v du
= (2x) × (√(π/4) × erf(2x)) - ∫√(π/4) × erf(2x) × 2 dx
= (2x) × (√(π/4) × erf(2x)) - 2√(π/4) × ∫erf(2x) dx
The integral ∫erf(2x) dx can be further simplified using substitution. Let's assign z = 2x, which implies dz = 2 dx. Substituting these values, we get:
∫erf(2x) dx = ∫erf(z) (dz/2) = (1/2) ∫erf(z) dz
Therefore, the final expression becomes:
∫(2x)\(e^{4x^{2} }\) dx = (2x) × (√(π/4) × erf(2x)) - √(π/2) × ∫erf(z) dz
Please note that the integral involving the error function cannot be expressed in terms of elementary functions and requires numerical or tabulated methods for evaluation.
Learn more about integral here:
https://brainly.com/question/31109342
#SPJ11
What are the 2 theoretical quantities of ANOVA?
Answers
The two theoretical quantities of ANOVA (Analysis of Variance) are:
1. Between-group variance.
2. Within-group variance:
1. Between-group variance.
This is the variance that can be attributed to differences between the group means.
It is calculated by comparing the mean of each group to the overall mean of all the data points.
The larger the between-group variance, the more likely there are significant differences between the groups.
2. Within-group variance:
This is the variance that can be attributed to differences within each group, i.e., the individual differences among the data points in each group.
It is calculated by comparing the individual data points in each group to their respective group mean.
The smaller the within-group variance, the more likely the groups are homogeneous.
In ANOVA, these two quantities are compared using an F-ratio.
If the between-group variance is significantly larger than the within-group variance, it indicates that there are significant differences between the group means, and the null hypothesis can be rejected.
For similar question on theoretical quantities.
https://brainly.com/question/30667471
#SPJ11
Please help me with this question step by step on how to solve it. It takes the earth 24 h to complete a full rotation. If it would take Mercury approximately 38 days, 10 h, and 30min to complete a full rotation. How many hours does it take Mercury to complete a full rotation? Show yourwork using the correct conversion factors.
Answers
In order to find the number of hours it takes to do the full rotation we separate into pieces the days, hours, and minutes and convert each of them separately.
using the conversion factor from days to hours we get that
\(1\text{day}=24\text{hours}\)then we get that
\(38\text{days}\cdot\frac{24\text{hours}}{1day}=912hours\)hours does not need a conversion factor, meaning that
\(10\text{hours}=10\text{hours}\)continue by converting the minutes using the following conversion factor
\(1\text{hour}=60\min \)then,
\(30\min \cdot\frac{1\text{hour}}{60\min }=0.5\text{hours}\)To complete add all the results together
\(\begin{gathered} 912+10+0.5 \\ 922.5\text{hours} \end{gathered}\)It takes mercury 922.5 hours to complete a full rotation.
Tom has 25 bumblebee marbles and Marcus has a few more than Tom. If they have 56 marbles in all, how many bumblebee marbles does Marcus have?
Answers
Answer:
56-25
= 31
Step-by-step explanation:
Answer: Marcus has 31 marbles
Step-by-step explanation: Tom has 25 marbles and there is 56 total so you subtract 25 from 56 and it sums up to 31. Your welcome.
Find the volume of this sphere.
Round to the nearest tenth.
16 ft
[ ? ] ft3
![Find the volume of this sphere.Round to the nearest tenth.16 ft[ ? ] ft3](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/4O631UUmVgkRfdb8IFRJJfkkTbGJlnqp.png)
Answers
Answer:
2144.7 ft^3Solution,
Diameter (d)=16 ft
Radius(r)=8 ft
Volume of sphere
\( = \frac{4}{3} \pi \: {r}^{3} \\ = \frac{4}{3} \times 3.14 \times {8}^{3} \\ = \frac{4}{3} \times 3.14 \times 512 \\ = 2144.7 \: {ft}^{3} \)
hope this helps..
Good luck on your assignment..
The answer to the question is 21473.4
Show 2 + 5 in number line.
Answers

A teacher wants to know whether their course helps students on the SAT. The hypothesized population mean for SAT scores is 500. The standard deviation of the population is 77. The sample size is 100. The sample mean for students who took the course is 533. What is the z-score
Answers
The z-score is -0.428
What is a z-score?A z-score, also known as a standard score, provides information on how far a data point is from the mean. Technically speaking, however, it's a measurement of how many standard deviations a raw score is from or above the population mean.
You can plot a z-score on a normal distribution curve.
You must be aware of the mean and population standard deviation to use a z-score.
Z-scores allow results to be compared to a "normal" population.
According to the question,
x=500
μ=533
σ=77
z-score=(x-μ)/σ
On substituting the values,
z-score=(500-533)/77
= -0.428
Learn more about z-scores here:
https://brainly.com/question/25638875
#SPJ4
The given planes intersect in a line. Find parametric equations for the line of intersection. [Hint: The line of intersection consists of all points (x, y, z) that satisfy both equations. Solve the system and designate the unconstrained variable as t .]
x + 2y + z = 1, 2x+5y + 32 = 4
Answers
The parametric equations for the line of intersection are:
x = 61 - 5t
y = 2t - 30
z = t
To find the parametric equations for the line of intersection of the given planes, we first need to solve the system of equations:
1. x + 2y + z = 1
2. 2x + 5y + 32 = 4
Step 1: Solve for x from equation 1:
x = 1 - 2y - z
Step 2: Substitute x in equation 2 with the expression found in step 1:
2(1 - 2y - z) + 5y + 32 = 4
Now we can use elimination to solve for one variable. Let's eliminate y by multiplying the first equation by 5 and subtracting it from the second equation:
Step 3: Simplify and solve for y:
2 - 4y - 2z + 5y + 32 = 4
y - 2z = -30
Step 4: Designate z as the parameter t:
z = t
Step 5: Substitute z with t in the expression for y:
y = 2t - 30
Step 6: Substitute z with t in the expression for x:
x = 1 - 2(2t - 30) - t
x = 1 - 4t + 60 - t
x = 61 - 5t
Now we have the parametric equations for the line of intersection:
x = 61 - 5t
y = 2t - 30
z = t
Note that we can choose any value of z for the parameter t, since z is unconstrained.
Learn more about Parametric:
brainly.com/question/15585522
#SPJ11
You paint four walls. Each wall is a rectangle with a length of 20 feet and a height of 12 feet. One gallon of paint covers about 320 square feet. How many gallons of paint do you need in order to cover the walls?Give explanation
Answers
Answer:
To find out how many gallons of paint are needed to cover the walls, we need to first find the total area of the walls.
The four walls are rectangles with a length of 20 feet and a height of 12 feet. So, the area of one wall is:
20 feet x 12 feet = 240 square feet
Since there are four walls, the total area of the walls is:
4 x 240 square feet = 960 square feet
We know that one gallon of paint can cover approximately 320 square feet. To find how many gallons of paint are needed, we can divide the total area of the walls by the area covered by one gallon of paint:
960 square feet ÷ 320 square feet per gallon = 3 gallons of paint
Therefore, you need approximately 3 gallons of paint to cover the walls.
Divide the polynomials.
Your answer should be a polynomial.

Answers
I hope that this is correct and that it helps✨❤️
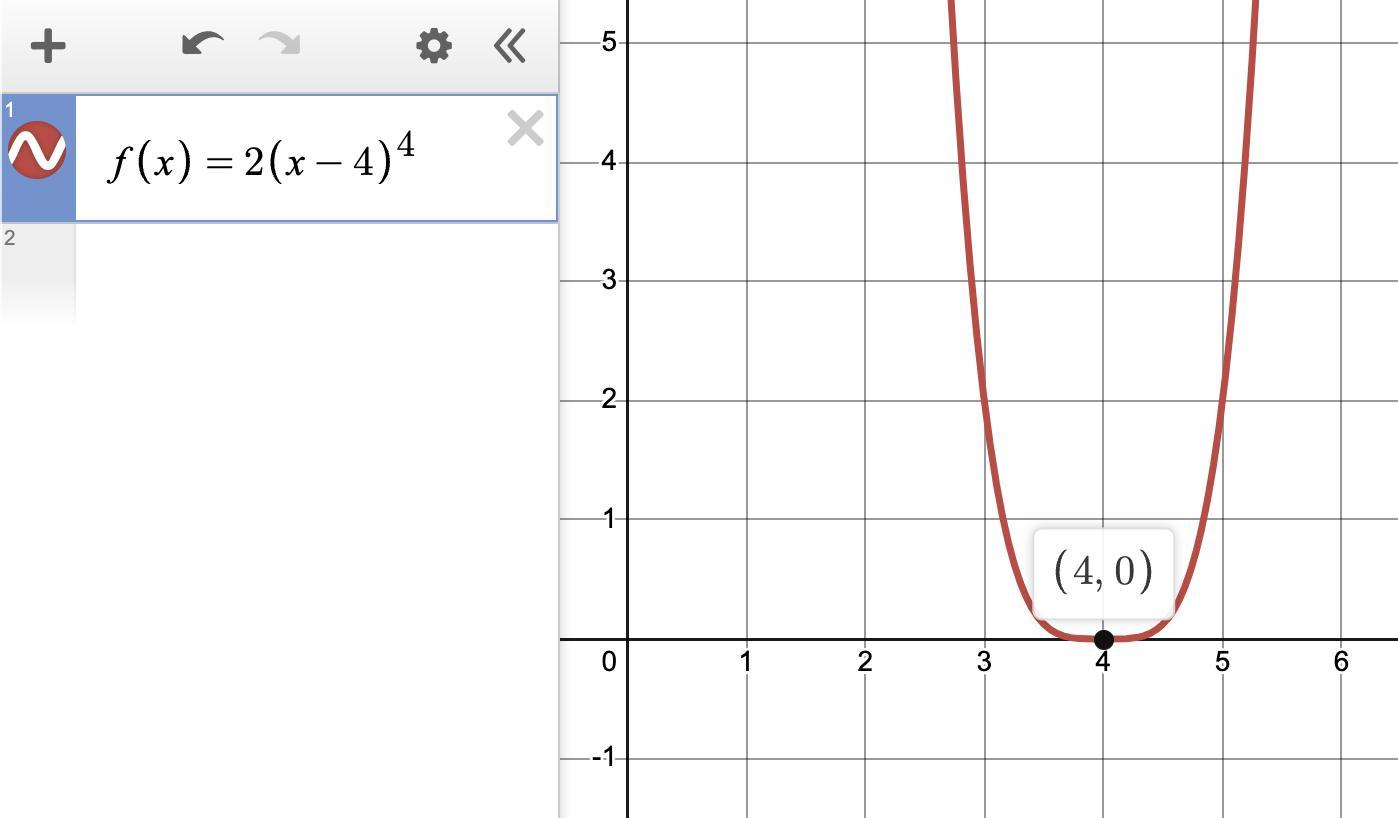
Question 1 of 10 Which statements describe the function f(x) = 2(x-4)4? A. It has 3 zeros and at most 4 relative maximums or minimums. B. It is a translation of the parent function 4 units to the left. C. It has 4 zeros and at most 3 relative maximums or minimums. D. Both ends of the graph of the function go up. E. The left end of the graph of the function goes up, and the right end goes down. F. It is a translation of the parent function 4 units to the right. SUBMiT
Answers
Answer:
C. It has 4 zeros and at most 3 relative maximums or minimums. D. Both ends of the graph of the function go up.F. It is a translation of the parent function 4 units to the right.Step-by-step explanation:
You want the statements that describe the function f(x) = 2(x -4)⁴.
DegreeThe degree of the function is the exponent: 4. This means the function has 4 zeros.
The maximum number of relative extrema is 1 less than the degree. The function has at most 3 relative maximums or minimums.
The even degree means both ends of the graph go in the same direction.
Leading coefficientThe leading coefficient of 2 is positive, so the ends of the function will go up.
Horizontal translationIn the parent function f(x) = x⁴, the value of x has been replaced by (x-4). This causes the graph to be translated 4 units to the right.
__
Additional comment
This function has a zero at (4, 0) with multiplicity 4. There is a flat spot where the graph touches, but does not cross, the x-axis. As a consequence, there is only one minimum and no relative maximums.
<95141404393>
1st quarter has 35 class days. As of today we have completed 28 of the 1st quarter class days. What % of 1st quarter class days have been completed?
Answers
Then multiply that fraction by a hundred this should give you 80%
The average earnings per share (EPS) for 9 industrial stocks randomly selected from those listed on the Dow-Jones Industrial Average (DJIA) was found to be 1.85 with a standard deviation of 0.395.
Calculate a 90% confidence interval for the average EPS of all the industrials listed on the DJIA.
Answers
To calculate the 90% confidence interval for the average EPS of all industrials listed on the DJIA, we will use the formula:
Confidence interval = sample mean ± (critical value * standard deviation / √sample size)
Step 1: Find the critical value.
Since we want a 90% confidence interval, the corresponding critical value can be obtained from the z-table. The critical value for a 90% confidence level is 1.645.
Step 2: Calculate the margin of error.
The margin of error is given by (critical value * standard deviation / √sample size).
Substituting the values, we get: 1.645 * 0.395 / √9 = 0.29175.
Step 3: Calculate the confidence interval.
The confidence interval is given by the sample mean ± margin of error.
Substituting the values, we get: 1.85 ± 0.29175.
The 90% confidence interval for the average EPS of all industrials listed on the DJIA is (1.55825, 2.14175).
We can be 90% confident that the true average EPS of all industrials listed on the DJIA falls within the range of 1.55825 to 2.14175.
To know more about calculate visit
https://brainly.com/question/32553819
#SPJ11
Your freind earn 7 1/2 dollar an hour Will he earn enough money to buy a $56 pair of headphone after working 4 3/4 hour?If not how much more money doe he need
Answers
Your friend does not earn enough money to buy the $56 headphones after working 4 3/4 hours. He will need 24 1/4 dollars more.
Let's first calculate the total amount of money your friend will earn after working 4 3/4 hours.
7 1/2 dollars per hour * 4 3/4 hours = 31 3/4 dollars
Now, let's compare this amount with the cost of the headphones:
31 3/4 dollars < 56 dollars
So, your friend does not earn enough money to buy the $56 headphones after working 4 3/4 hours. He will need 56 - 31 3/4 = 24 1/4 dollars more.
To learn more about earn here:
https://brainly.com/question/29249141
#SPJ4
What is the rectangular equivalence to the parametric equations?
x(θ)=2sinθ+1,y(θ)=3cosθ−2 , where 0≤θ<2π .
Drag a term into each box to correctly complete the rectangular equation.

Answers
Notice that
(x - 1)²/4 + (y + 2)²/9 = (2 sin(θ))²/4 + (3 cos(θ))²/9
… = sin²(θ) + cos²(θ)
… = 1
Solve for y in terms of x :
(x - 1)²/4 + (y + 2)²/9 = 1
(y + 2)²/9 = 1 - (x - 1)²/4
(y + 2)² = 9 - 9/4 (x - 1)²
y + 2 = ± √(9 - 9/4 (x - 1)²)
y + 2 = ± 3/2 √(4 - (x - 1)²)
y = -2 ± 3/2 √(4 - (x - 1)²)
In order for the square root to be defined, one needs
4 - (x - 1)² ≥ 0
(x - 1)² ≤ 4
-2 ≤ x - 1 ≤ 2
-1 ≤ x ≤ 3
so x must belong to the interval [-1, 3].
The height of a triangle is 8 cm more than the base. If the area is 24 cm2, find the height and base of the triangle.
Answers
Answer:
height = 12 cm
base length = 4 cm
Step-by-step explanation:
area of a triangle
base length × height / 2
x = height
y = base length
x = y + 8
24 = y × (y + 8) / 2
48 = y × (y + 8) = y² + 8y
squared equation
y² + 8y - 48 = 0
solution
y = (-b ± sqrt(b² - 4ac))/(2a)
a = 1
b = 8
c = -48
y = (-8 ± sqrt(64 - 4×-48))/2 = (-8 ± sqrt(64 + 192))/2 =
= (-8 ± sqrt(256))/2 = (-8 ± 16)/2 = -4 ± 8
y1 = -4 + 8 = 4 cm
y2 = -4 - 8 = -12
but a negative base length did not make any sense, so only y = 4 remains.
x = y + 8 = 4 + 8 = 12 cm
Solve unit rate problems- what name should be in the correct blank spot?

Answers
Carl types 54 WPM
Max types 52 WPM
Jason types 59 WPM
So the answer is Max-Carl-Jason
Hope this helped
Find the area of ABC with vertices A(4, -3) B(9,-3) , and C(10, −11)
Answers
The area of triangle ABC with vertices is 22 square units
How to find the area of ABC with vertices?The vertices are given as:
A(4, -3) B(9,-3) , and C(10, −11)
The area of the triangle is calculated using
Area = 0.5 * |Ax(By - Cy) + Bx(Ay - Cy) + Cx(Ay - By)|
This gives
Area = 0.5 * |4 * (-3 + 11) + 9 * (-3 + 11) + 10 * (-3 - 3)|
Evaluate the sum of products
Area = 0.5 * |44|
Remove the absolute bracket
Area = 0.5 * 44
Evaluate
Area = 22
Hence, the area of ABC with vertices is 22 square units
Read more about areas at:
https://brainly.com/question/22972014
#SPJ1
For a normal distribution, the skewness and kurtosis measures are as follows: O A. 1 and 2 B. 0 and 3. OC. O and 0. OD. 1.96 and 4.
Answers
For a normal distribution, the skewness and kurtosis measures are as follows: Option B. 0 and 3.
Skewness is a measure of the asymmetry of a probability distribution. Skewness is a measure of the degree of asymmetry in the probability distribution of a random variable around its mean.
When the skewness is 0, the normal distribution is symmetrical.
Kurtosis is a measure of the degree of peakiness, or flatness, of a probability distribution.
For a normal distribution, kurtosis equals 3. In comparison to the normal distribution, distributions with kurtosis greater than 3 have a more pointed peak and longer tails, while distributions with kurtosis less than 3 have a less pointed peak and shorter tails.
Therefore, for a normal distribution, the skewness and kurtosis measures are 0 and 3, respectively. Hence, the correct option is B. 0 and 3.
To more about Skewness:
https://brainly.com/question/15422644
#SPJ11
Someone help me please

Answers
Answer:
option a
Step-by-step explanation:
all positive real numbers