Given: Triangle ABC is similar to triangle DEF, side BC = 19, angle ABC = 48, angle BCA = 73.
If the side DF = 15, then AB - EF = ?
Answers
Answer:
We are given two similar triangles, triangle ABC and triangle DEF, and some measurements of triangle ABC. We are also given that DF, one of the sides of triangle DEF, is equal to 15 units. Using this information, we are asked to find the difference between the lengths of sides AB and EF.
To solve the problem, we can first use the angle-angle similarity theorem to determine that the corresponding angles of the two triangles are equal. Therefore, angle DEF is equal to angle BCA, and angle ABE is equal to angle DFE.
Next, we can use the law of sines to find the length of side AB. The law of sines states that the ratio of the length of a side of a triangle to the sine of the angle opposite that side is equal for all sides and angles in the triangle. Applying this to triangle ABC, we have:
AB/sin(73) = BC/sin(48)
Substituting the value of BC as 19 units, we can solve for AB to get:
AB = 22.78 units
Similarly, we can use the law of sines to find the length of side EF. Since angle DFE is equal to angle ABE, we can use the same ratio as above to get:
EF/sin(73) = DF/sin(48)
Substituting the value of DF as 15 units, we can solve for EF to get:
EF = 18.20 units
Finally, we can subtract EF from AB to get:
AB - EF = 22.78 - 18.20 = 4.58 units
Therefore, the difference between the lengths of sides AB and EF is 4.58 units.
Related Questions
Runge-Kutta method 4th order derivative C program
3. Design a C program for Runge-Kutta method of 4th order to solve a first order Ordinary Differential Equation with initial condition and hence solve the D.E. y' = y - 2xy, y(0) = 1 by R-K method wit
Answers
The C program for RK 4th order .
C program,
#include<stdio.h>
//differential equation "dy/dx = (y-2*x*y)"
float f(float x, float y)
{
return(y-2*x*y);
}
int main()
{
// Finds value of y for a given x using step size h
int i,n;
float x0,y0,x,h,k1,k2,k3,k4;
printf("Enter the value of x:");
scanf("%f",&x);
//initial value y0 at x0.
printf("Enter the initial value of x & y:");
scanf("%f%f",&x0,&y0);
//step size
printf("Enter the value of h:");
scanf("%f",&h);
//prints the initial value of y at x and step size.
printf("x0=%f\t yo=%f\t h=%f\n",x0,y0,h);
//Count number of iterations using step size or
//step height h
n=(x-x0)/h;
// Iterate for number of iterations
for(i=1;i<=n;i++)
{
//Apply Runge Kutta Formulas to find
//next value of y
k1 = h*f(x0,y0);
k2 = h*f(x0+h/2,y0+k1/2);
k3 = h*f(x0+h/2,y0+k2/2);
k4 = h*f(x0+h,y0+k3);
//Update next value of y
y0 = y0+(k1+2*k2+2*k3+k4)/6;
//Update next value of x
x0=x0+h;
}
//print the value of y at entered value of x.
printf("at x=%f\t,y=%f\n",x,y0);
return 0;
}
Solution of DE,
y' = y - 2xy, y(0) = 1
The task is to find value of unknown function y at a given point x.
Below is the formula used to compute next value yn+1 from previous value yn. The value of n are 0, 1, 2, 3, ….(x – x0)/h.
Here h is step height and xn+1 = x0 + h
\(K_{1} = h f(x_{n} ,y_{n} )\)
\(K_{2} = hf( x_{n} + h/2 , y_{n} + K_{1}/2 )\)
Thus,
\(y_{n+1} = y_{n} + K_{1} / 6 + K_{2} / 3 + K_{3} / 3 + K_{4} / 6 +O(h^{5} )\)
Know more about C program,
https://brainly.com/question/30905580?referrer=searchResults
#SPJ4
a. For the function and point below, find f'(a). b. Determine an equation of the line tangent to the graph of f at (a,f(a)) for the given value of a. f(x) = 3x^2 + 2x, a = -2
Answers
For f'(a) is given by f'(a) = 6a + 2 and equation of the line tangent to the graph is y = -10x - 12.
f(x) = 3x² + 2x
f'(x) = 6x + 2
So f'(a) = f'(-2) = -12+2 = -10
In order to find tangent line , we need a slope and a point. We have the x-co-ordinate for our point, so we can plug that in to find Y-coordinate.
F(-2) = 8
The slope of tangent line is the derivative at this point , f'(-2) = -10
Equation of line tangent,
y - 8 = -10(x - (-2))
y = -10x - 12.
The limit of a function in mathematics is a key idea in calculus and analysis regarding the behavior of that function close to a specific input.
Informally, a function f gives each input x an output f(x). If f(x) approaches L as x approaches input p, we say that the function has a limit L at that location. More specifically, any input that is sufficiently close to p when f is applied forces the output value arbitrarily close to L.
The concept of limit is specifically used in the various definitions of continuity. Roughly speaking, a function is continuous if all of its limits agree with the values of the function. The term "limit" is also used in the definition of the mathematical term "derivative," which in one-variable calculus refers to the maximum value of the slope of secant lines on a function's graph.
To learn more about Limits:
brainly.com/question/282767
#SPJ4
Amanda and Alexis live 4 miles apart. They decide to start walking toward each other’s houses at the same time. Amanda walks at a rate of 3.5 miles per hour and Alexis walks at a rate of 4 miles per hour. How long will it take for them to meet? Round to the nearest hundredth of an hour. [Remember: D = (r)(t)]
Answers
Answer:
0.53 hours
Step-by-step explanation:
D = (r)(t), Where
‘D’ is the distance covered
‘r’ is the approach rate
‘t’ is the total time spent
Distance covered, ‘D’ = 4 miles
Approach rate, “r” = 3.5mph + 4mph
r = 7.5mph.
t is unknown
Solving for t,
D = (r)(t)
4 = 7.5t
t = 4/7.5
t = 0.53 hours (to the nearest hundredth)
Therefore, it will take Amanda and Alexis 0.53 hours to meet
Someone help me with this please

Answers
Answer:
Hi, there the answer is -1
Step-by-step explanation:
Need 6 and 7 done please and thank you

Answers
Answer:
black
black
Step-by-step explanation:
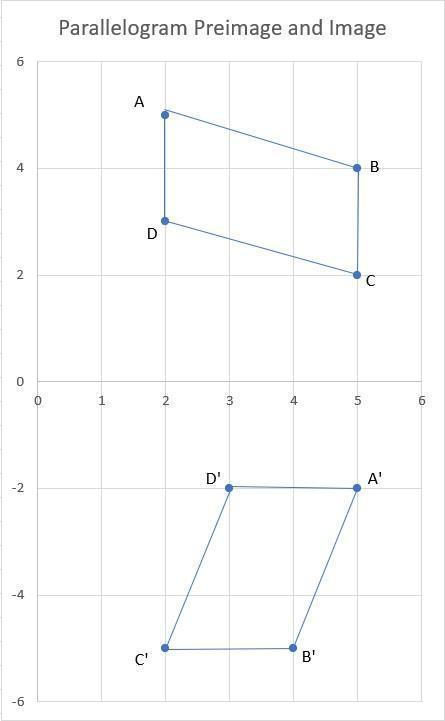
Parallelogram ABCD is rotated to create image A'B'C'D'.
Answers
The transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
The rule that describes the transformation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
To understand this, let's apply the transformation rule to each vertex of the original parallelogram ABCD:
Point A (2, 5) becomes A' (-5, 2).
Point B (5, 4) becomes B' (-4, 5).
Point C (5, 2) becomes C' (-2, 5).
Point D (2, 3) becomes D' (-3, 2).
By applying the transformation rule, we observe that the x-coordinate of each point becomes the negative of the original y-coordinate, and the y-coordinate becomes the original x-coordinate.
This transformation is a 90-degree counterclockwise rotation about the origin (0, 0) on the coordinate plane. The image parallelogram A'B'C'D' is obtained by rotating the original parallelogram ABCD by 90 degrees counterclockwise.
Visually, this transformation can be seen as the original parallelogram being rotated around the origin, where the x-axis becomes the y-axis, and the y-axis becomes the negative x-axis.
Therefore, the transformation rule that describes the rotation from the original parallelogram ABCD to the image parallelogram A'B'C'D' is (x, y) → (–y, x).
For more such questions on parallelogram visit:
https://brainly.com/question/970600
#SPJ8
Can you please simplify these expressions in two forms: radical and simplified without exponents?
I don't really understand how fractional exponents work, so an explanation would be appreciated.
27^4/3
36^3/2
(1/8)^2/3
128^5/7
Thank you :)
Answers
Answer:
(a.) 27^4/3 = 81, (b.) 36^3/2 = 216, (c.) (1/8)^2/3 = 1/4, (d.) 128^5/7 = 32
Step-by-step explanation:
All these expressions can be converted in square roots.
In order to do this, we can picture the fractional exponents as exponent / index
(a.) So for this first problem, we would have the cube root of \(27^{\frac{4}{3} }\) or
\(\sqrt[3]{(27)^{4} }\).
We must do the equation inside the radical first (i.e., \((27)^{4}\)) to get \(\sqrt[3]{531,441}\) = 81
We can follow these same steps for the remaining equations:
(b.) \(36^{\frac{3}{2} }\) = \(\sqrt{(36)^3}\) = \(\sqrt{46,656}\) = 216
(c.) \((\frac{1}{8})^\frac{2}{3}\) = \(\sqrt[3]{(\frac{1}{8})^{2} }\) = \(\sqrt[3]{(\frac{1^2}{8^2}) }\) = \(\sqrt[3]{(\frac{1}{64}) }\) = \(\frac{1}{4}\)
(d.) \(128^{\frac{5}{7} }\) = \(\sqrt[7]{(128)^{5} }\) = 32
The manager of a computer retails store is concerned that his suppliers have been giving him laptop computers with lower than average quality. His research shows that replacement times for the model laptop of concern are normally distributed with a mean of 3.1 years and a standard deviation of 0.5 years. He then randomly selects records on 49 laptops sold in the past and finds that the mean replacement time is 2.9 years. Assuming that the laptop replacement times have a mean of 3.1 years and a standard deviation of 0.5 years, find the probability that 49 randomly selected laptops will have a mean replacement time of 2.9 years or less.
Answers
The probability that 49 randomly selected laptops will have a mean replacement time of 2.9 years or less can be calculated using the z-score and the standard normal distribution.
To find the probability, we first calculate the z-score using the formula:
z = (x - μ) / (σ / √n)
where x is the sample mean (2.9 years), μ is the population mean (3.1 years), σ is the population standard deviation (0.5 years), and n is the sample size (49 laptops).
Plugging in the values, we have:
z = (2.9 - 3.1) / (0.5 / √49)
z = -0.2 / (0.5 / 7)
z = -0.2 / 0.0714
z ≈ -2.80
Next, we use a standard normal distribution table or calculator to find the probability corresponding to the z-score of -2.80. The probability can be found as the area under the curve to the left of the z-score.
By calculating the z-score, we standardize the sample mean with respect to the population mean and standard deviation. This allows us to compare the sample mean to the population distribution.
The negative z-score indicates that the sample mean of 2.9 years is below the population mean of 3.1 years. By looking up the corresponding probability from the standard normal distribution, we find that it is very unlikely to obtain a sample mean of 2.9 years or less by chance alone.
To know more about z-scores , refer here:
https://brainly.com/question/31871890#
#SPJ11
If f(x)=-3x² +1, then which of the following is the value of f(-2)?
a) -11
b) 37
c) -35
d) -37
Answers
Answer:
A, -11
Step-by-step explanation:
f(x)=-3x(-2)+1
=-3(4)+1
=-12+1
=-11
Step-by-step explanation:
f(x)=3x²+1
f(-2)=3(-2)²+1
= -12+1
=-13 ans
Which expression is equal to 75√?
75√25
75√5
355√
4935√
Answers
Answer:
B
Step-by-step explanation:
Assume the probabilities of a child being allergic to the following foods are as follows:
.014 for nuts
.043 for dairy
.031 for gluten
Calculate the probability that a child is NOT allergic to nuts.
Answers
The probability that a child is not allergic to nuts is 0.986, or 98.6%.
The probability that a child is not allergic to nuts can be calculated by subtracting the probability of being allergic to nuts from 1.
Given the probabilities of a child being allergic to nuts, dairy, and gluten, we are interested in finding the probability that a child is not allergic to nuts.
The probability of being allergic to nuts is given as 0.014.
To find the probability that a child is not allergic to nuts, we subtract this value from 1.
P(Not allergic to nuts) = 1 - P(Allergic to nuts) = 1 - 0.014 = 0.986
Therefore, the probability that a child is not allergic to nuts is 0.986, or 98.6%.
This calculation is based on the assumption that being allergic to nuts and being allergic to other foods are independent events.
Learn more about Probability here:
brainly.com/question/15052059
#SPJ11
A membership sales person at a gym is given a choice of two different compensation plans. One plan offers a weekly salary of $300 plus a commision of $15 for each membership sold. The other plan offers no salary but pays $30 commission on each membership sold. How many memberships must the salesperson sell to make the same amount of money under both plans? FAST PLS
Answers
Answer: The salesperson must sell 20 memberships to make the same amount of money under both plans.
Step-by-step explanation:
Let x be the number of memberships.
In first plan,
Weekly salary of $300 plus a commission of $15 for each membership sold.
i.e. Earning (weekly) = 300+15x
In second plan,
The other plan offers no salary but pays $30 commission on each membership sold.
i.e. earning = 30x
According to the question, when \(300+15x=30x\)
\(\Rightarrow\ 300=30x-15x\\\\\Rightarrow\ 300=15x\\\\\Rightarrow\ x=\dfrac{300}{15}\\\\\Rightarrow\ x=20\)
Hence, the salesperson must sell 20 memberships to make the same amount of money under both plans.
Pls help me before brainlly deletes qeustion hurry 10 points for whoever help me

Answers
Answer:
\(x=\frac{2}{7}\)
Step-by-step explanation:
\(x^{2}=\frac{4}{49}\)
\(\sqrt{x^2}=\sqrt{\frac{4}{49}\)
\(x=\pm\frac{2}{7}\)
Since we only want the positive value, then \(x=\frac{2}{7}\) is correct.
Find the midpoint of the segment with the following endpoints.
(2, 4) and (6, 8)
Answers
Answer:
Halfway between x = 2 and x = 4 is x =3 , and halfway between y = 8 and
y = 6 is at y =7, so the midpoint is (3, 7) .
Step-by-step explanation:
Elmer spent the day at the mall. First, he bought five rabbits for $10 each. Later, he bought four cupboards for $70 each. After that, he found a twenty dollar bill. Also, he returned one rabbit. Write the total change to Elmer's funds as an integer.
Answers
Answer:
-300
Step-by-step explanation:
Step 1: Find the amount Elmer's funds decreased after purchasing the rabbits:
Let x represent Elmer's funds.
Since Elmer bought five rabbits for $10 each, he lost $10 5 times.
x - (10 * 5)
x - 50
Thus, Elmer lost (spent) $50 for the 5 rabbits.
Step 2: Find the amount Elmer's funds decreased after purchasing the cupboards:
Since Elmer bought four cupboards for $70 each, he lost $70 4 times:
x - (50 + (70 * 4))
x - (50 + 280)
x - 330
Thus, after purchasing the rabbits and cupboards, Elmer lost $330.
Step 3: Find the amount Elmer's funds increased after finding the twenty-dollar bill:
Since Elmer found a twenty-dollar bill, he gained $20
x - (330 + 20)
x - 310
Step 4: Find the amount Elmer's funds increased after returning one rabbit:
Since Elmer returned one rabbit, he gained $10:
x - (310 + 10)
x - 300
Thus, Elmer's funds changed totally by -$300.
Putting all the information together, we have:
x - 10 - 10 - 10 - 10 - 10 - 70 - 70 - 70 - 70 + 20 + 10
x - 50 - 280 + 30
x - 330 + 30
x - $300
Suppose that a particular brand of 5 inch candles has an average life of 27 hours with a standard deviation of six hours. If all possible samples of 4 candles were selected in the average life of the samples was determined, what would the mean of the distribution of the sample means be?
5
3
4
27
Answers
The mean of the distribution of sample means would be 27 hours, which is the same as the average life of the candles.
This is because the sample means would be expected to be centered around the population mean.
The standard deviation of the distribution of sample means (also known as the standard error of the mean) can be calculated using the formula:
standard deviation of sample means = standard deviation of population / square root of sample size
In this case, the standard deviation of sample means would be:
6 / square root of 4 = 3
So the answer is 3.
So, the mean of the distribution of the sample means would be 3. Your answer: 3.
To learn more about mean : brainly.com/question/31101410
#SPJ11
GIVING BRAINLIEST!!!!!
What type of triangle is shown in the image?
Acute triangle
Right triangle
Equilateral triangle
Obtuse triangle

Answers
Answer:
A. Obtuse triangle
B,C,D. Acute
Step-by-step explanation:
suppose that iq scores have a bell-shaped distribution with a mean of 101 and a standard deviation of 12 . using the empirical rule, what percentage of iq scores are between 77 and 125 ?
Answers
According to the empirical rule of IQ scores no higher than 125 and less than 77, the percentage is found to be 97.5%.
From the above data, we can determine the mean (U) and standard deviation (p), which are respectively 101 and 12.
And we're looking for the percentage that isn't greater than 125. We can utilise the calculation for the z score, which is as follows: z = X-U/p X is the percentage,
And by using the value provided, we obtained: z = (125-101)/12
z = 2.
According to the empirical rule, 95% of the values fall between two standard deviations, while 5% fall in the tails.
As a result the percentage is required to be less than the 2 standard deviation but above the mean which is equal to (100-2.5)=97.5%.
To know more about standard deviation and mean, visit,
https://brainly.com/question/24298037
#SPJ4
Nicholas bought 3 cartons of confetti eggs. Each carton contained 12 confetti eggs. One package
of confetti eggs hadi 4 broken.
Answers
Answer:
3 times 12 equals 36. 36-4=32. The answer is 32
Step-by-step explanation:
how can we use models to estimate percent questions? Give examples to support your answer.
Answers
Answer:
Percent questions can be estimated using models by dividing the given number by the total number of parts in the model. For example, if there are ten students in a classroom and 30 candy bars, then each student would get three candy bars. Another example would be if there are ten students in a classroom and 30 candy bars, and one student takes five candy bars, then the remaining nine students would get two candy bars each.
Answer:
Percent questions can be estimated using models by dividing the given number by the total number of parts in the model. For example, if there are ten students in a classroom and 30 candy bars, then each student would get three candy bars. Another example would be if there are ten students in a classroom and 30 candy bars, and one student takes five candy bars, then the remaining nine students would get two candy bars eac
Step-by-step explanation:
determine the rate constantof inactivation assuming the chick-watson model applies with an n value of 1.0.
Answers
The rate constant of inactivation is -0.6538 \(s^{-1}\).
To determine the rate constant of inactivation using the Chick-Watson model, we need to plot the natural logarithm of the surviving fraction of the virus (N/N₀) against time (t) and fit a linear regression to the data. The Chick-Watson model is given by the equation:
ln(N/N₀) = -kt
Where:
N₀ is the initial number of viruses (\(10^{6}\))
N is the number of viruses at time t
k is the rate constant of inactivation
Let's calculate the surviving fraction (N/N₀) and perform the linear regression:
Time (s) | N/N₀ | ln(N/N₀)
0 | 1.0 | 0.0
2 | 0.2 | -1.61
4 | 0.01 | -4.60
6 | 0.0015 | -6.50
8 | 0.0001 | -9.21
Using the given data, we can perform linear regression on the ln(N/N₀) values against time (t) values to determine the rate constant (k).
Let's calculate the rate constant (k) using linear regression:
Sum of ln(N/N₀) = -21.92
Sum of t = 20
Sum of (\(t^{2}\)) = 120
Mean of ln(N/N₀) = (-21.92) / 5 = -4.384
Mean of t = 20 / 5 = 4
Mean of (\(t^{2}\)) = 120 / 5 = 24
Sum of [(t - mean(t)) * (ln(N/N₀) - mean(ln(N/N₀)))] = -52.304
Sum of \((t-mean(t))^{2}\) = 80
Using the linear regression formula:
k = [Sum of [(t - mean(t)) * (ln(N/N₀) - mean(ln(N/N₀)))]] / [Sum of \((t-mean(t))^{2}\) ]
k = -52.304 / 80 = -0.6538
Therefore, the rate constant of inactivation for NH2Cl disinfection of MS2 bacteriophage at a concentration of 2 mg/L is approximately -0.6538 \(s^{-1}\).
Correct Question :
The data for NH2Cl disinfection of MS2 bacteriophage at a concentration of 2 mg/L is shown below. The temperature was 20 °C, the pH was 6.0. Determine the rate constant of inactivation assuming the Chick-Watson model applies with an n value of 1.0.
Time (s) 0 2 4 6 8
Number of virus \(10^{6}\) 0.2*\(10^{6}\) 0.1*\(10^{5}\) 0.15*\(10^{4}\) 0.1*\(10^{3}\)
To learn more about rate constant here:
https://brainly.com/question/31197553
#SPJ4
what is the answer to 5x-4y=3
Answers
Answer: we need to get the values of x and y
x=(4y+3)/5
y=(5x-3)/4
Step-by-step explanation:
let us consider the quation 5x-4y=3
then on adding 4y on both sides it becomes:
5x=3+4y
this equation is in standard form
divide by 5 on both sides
it becomes
x=(3+4y)/5
in the similar way subtract 5x on both sides
then we get -4y=3-5x
it becomes: 4y=5x-3
y=(5x-3)/4
Step by step
We can solve x and y in standard form by substituting zero (0) for x to solve for y and (0) for y to solve x
5(0) -4y = 3
Simplify
-4y = 3
Divide both sides by -4 to solve for y
-4/-4 y = 3/-4
Simplify
y = -3/4
5x -4(0) = 3
Simplify
5x = 3
Divide both sides by 5 to solve for x
5/5 x = 3/5
Simplify
x = 3/5
Jason is a high school basketball player. In a particular game, he made some free
throws (worth one point each) and some two point shots. Jason made a total of 13
shots altogether and scored a total of 20 points. Write a system of equations that
could be used to determine the number of free throws Jason made and the number of
two point shots he made. Define the variables that you use to write the system.
Answers
The total number of free throws shots Jason made was 6 and the total number of two point shots Jason made was 7.
First, let us understand the variables:
Any number, vector, matrix, function, its argument, set, or one of its elements can be specifically represented by a variable.
Let x and y be the quantity of shorts.
x is the number of attempts at the free throw line.
y is the quantity of two-point attempts.
According to the question, we have;
x + 2y = 20 ............equation 1
x + y = 13 ............equation 2
From equation 2 we can take out the value of x;
x = 13 - y ............equation 3
substituting the value of x in equation 1, we will get;
(13 - y) + 2y = 20
13 - y + 2y = 20
13 + y = 20
y = 20 - 13
y = 7
putting the value of y in equation 3, we will get
x = 13 - 7
x = 6
Thus, the total number of free throws shots Jason made was 6 and the total number of two point shots Jason made was 7.
To learn more about variables visit:
https://brainly.com/question/28248724
#SPJ1
one angle of a triangle measures 20 and the other two angles are in a ratio of 3:5 what are the measures of the 2 angles
Answers
Answer:
60 and 100 degrees.
Step-by-step explanation:
Sum of the other 2 angles = 180-20 = 160 degrees.
3 + 5 = 8
160 / 8 = 20
- so the other 2 angles are:
3*20 = 60 and
5*20 = 100 degrees.
The double number line below shows the approximate number of pounds in a certain number of kilograms: Based on the nunber line, about how many pounds are there In 4.5 kilograms?
1. 8
2. 9
3. 10
4. 11
Answers
Rich Borne teaches Chemistry 101. Last week he gave his students a quiz. Their scores are listed below. 24 31 47 29 31 16 48 41 50 54 37 22 54 38 7 16
Answers
The quiz scores of Rich Borne's Chemistry 101 students are as follows: 24, 31, 47, 29, 31, 16, 48, 41, 50, 54, 37, 22, 54, 38, 7, and 16.the performance of Rich Borne's Chemistry 101 students on the quiz
To analyze this data, we can calculate various descriptive statistics such as the mean, median, mode, range, and standard deviation. The mean (average) score can be obtained by summing up all the scores and dividing by the total number of scores. The median represents the middle value when the scores are arranged in ascending order. The mode refers to the most frequently occurring score. The range is the difference between the highest and lowest scores, indicating the spread of the data. The standard deviation measures the variability or dispersion of the scores around the mean.
By calculating these descriptive statistics, we can gain insights into the performance of Rich Borne's Chemistry 101 students on the quiz and understand the central tendency and variability of their scores.
know more about descriptive statistics :brainly.com/question/30764358
#SPJ11
Jane divides 3 pounds of fudge among 5 people. How much fudge does each person receive?
A)
3
5
lb
B)
2
5
lb
C)
1
2
lb
D)
3
4
lb
Answers
Answer:
A
Step-by-step explanation:
3/5th of a pound each. This is common knowledge but its 100% A
The correct answer is A because everyone will get 3/5 of it
Write the equation of the line perpendicular to y−5=12(x+9) that passes through the point (–1,–1).
Answers
Rewrite the equation in slope-intercept form::
\(y-5=12(x+9)\\y-5=12x+108\\y=12x+108-5\\y=12x+103\)
According to the slope-intercept form of the line equation, slope of the equation is \(m_1=12\).
Because another line is perpendicular to \(y=12x+103\), the slope of another line:
\(m_1 \times m_2=-1\\12\times m_2=-1\\m_2=-\frac{1}{12}\)
Substitute \(m_2=-\frac{1}{12}\) and the point \((-1,-1)\) into the equation form:
\(y-y_1=m_2(x-x_1)\\y-(-1)=-\frac{1}{12}(x-(-1))\\y+1=-\frac{1}{12}(x+1)\\------------\times12\\12y+12=-(x+1)\\12y+12=-x-1\\x+12y+12+1=0\\x+12y+13=0\)
Hence the equation of the line is \(x+12y+13=0\).
Learn more about the equation of a line here: https://brainly.com/question/28695475
#SPJ1
what is the answer to 26= 8 + v
Answers
Explanation: if 26 is equal to 8 + v, then you’d have to subtract 8 from 26 to get v. I know this because then when you add 18 (v) and 8 together, you’ll get an equal if 26.
statistical power is a measure of the ability to reject the null hypothesis when:
Answers
Statistical power is a measure of the ability to reject the null hypothesis when it is false. It represents the probability of correctly identifying a true effect or relationship in a statistical hypothesis test.
A high statistical power indicates a greater likelihood of detecting a significant result if the null hypothesis is indeed incorrect. The power of a statistical test depends on several factors, including the sample size, the effect size (the magnitude of the true effect or difference), the chosen significance level (often denoted as α), and the variability or noise in the data. Increasing the sample size or effect size generally increases the statistical power, while a lower significance level or higher variability decreases it.
Power analysis is commonly used to determine an appropriate sample size for a study, ensuring that it is adequately powered to detect the desired effect. A higher power is desirable as it reduces the chances of a Type II error (failing to reject the null hypothesis when it is false) and increases the chances of correctly detecting real effects or relationships.
Learn more about null hypothesis here:
https://brainly.com/question/29387900
#SPJ11