Answers
Answer:
x=-1
Step-by-step explanation:
I'm weird and love these types of problems.
Ok first off we need to get x alone. To do that we need to first get rid of the 7.
We can do that by adding it because you have to use the opposite operation to get rid of it.
5x - 7 (+7) = -12 (+7)
See if you add -7 + 7 you get 0 which is why you have to use the opposite.
5x = -5
To get x alone you have to divide 5 because 5 is being multiplied by x.
5x(/5) = -5(/5)
x= -1
So x= -1
If you ever need more help, don't be afraid to reach out. I hope that helps!
Answer:
I think it is -1
Step-by-step explanation:
Because -1 x 5 equals -5 and -5 - 7 equals - 12
Related Questions
A basketball team scored 50 points in a game last week. This week, they scored 55 points. What was the percent increase in points scored from last week to this week?
Answers
What is 3 3/7 rounded to the nearest whole number
Answers
Answer:
0
Step-by-step explanation:
If you insist on converting 3/7 to a whole number, the best we can do is round the decimal number up or down to the nearest whole number. 3/7 rounded up to the nearest whole number is 1 and 3/7 rounded down to the nearest whole number is 0.
Help meh plz thx ☝︎︎

Answers
Answer:
sponge b00b
Step-by-step explanation:
Suppose you can spend no more than 15 hours a week at your two jobs. Mowing lawns pays $3 an hour and babysitting pays $5 an hour. You need to earn at least $60 a week.
Answers
The common region to both the graphs represents the solution set of the given inequalities.
What are algebraic expressions?In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context.
Given is that you can spend no more than 15 hours a week at your two jobs. Mowing lawns pays $3 an hour and babysitting pays $5 an hour. You need to earn at least $60 a week.
Assume that you worked {x} hours Mowing lawns and {y} hours babysitting.
We can write the inequalities as -
x + y ≤ 15
3x + 5y ≥ 60
Refer to the graph attached. The common region to both the graphs represents the solution set.
Therefore, the common region to both the graphs represents the solution set of the given inequalities.
To solve more questions on functions & expressions, visit the link below
brainly.com/question/17613163
#SPJ9

PLEASE HeLEp
A six-sided composite figure. A vertical line on the left is labeled 8 meters. The base is labeled 18 meters. There is a small portion from the vertical line that is parallel to the base that is labeled 6 meters. This portion leads to two segments that come to a point, and from that point, there is a height of 8 meters labeled.
What is the total area of the figure?
192 m2
216 m2
288 m2
336 m2
Answers
Answer:
To find the area of the six-sided composite figure, we can divide it into two smaller shapes: a rectangle and a triangle.
The rectangle has a length of 8 meters and a width of 18 meters, so its area is:
8 meters × 18 meters = 144 square meters
The triangle has a base of 18 meters and a height of 8 meters, so its area is:
(1/2) × 18 meters × 8 meters = 72 square meters
The total area of the six-sided composite figure is the sum of the areas of the rectangle and the triangle:
144 square meters + 72 square meters = 216 square meters
Therefore, the total area of the figure is 216 m².
Option (B) 216 m²
Step-by-step explanation:GIVEN
Vertical line on the left is labeled 10 meters. The base is labeled 18 meters. there is a small portion from the vertical line that is parallel to the base that is labeled 5 meters. this portion leads to two segments that come to a point, and from that point, there is a height of 2 meters labeled.
TO FIND
The area of the figure.
SOLUTION
The above problem can be simply solved as follows —
The composite figure is rectangle and 2 triangles.
Length of the Rectangle = 10 meters
Width of Rectangle = 18 meters
Area of Rectangle = Length × Breath
= 10 × 18
= 180 meter²
Base of Triangle = 18 meters
Height of Triangle = 2 meters
Area of Triangle = (1/2) × base × height
= (1/2) × 18 × 2
= (1/2) * 36
= 18 m²
Total number of triangles = 2
Total area of Triangles = Area of triangle * Number of Triangles
= 18 * 2
= 36 m²
Total area of the figure = 36 + 180 = 216 m²
Hence, The answer is 216 m².
Hope my answer helps you.
:)
Please mark my answer as the BRAINLIEST. Plssssssssssssssssssss
find the domain & range, pls helpp
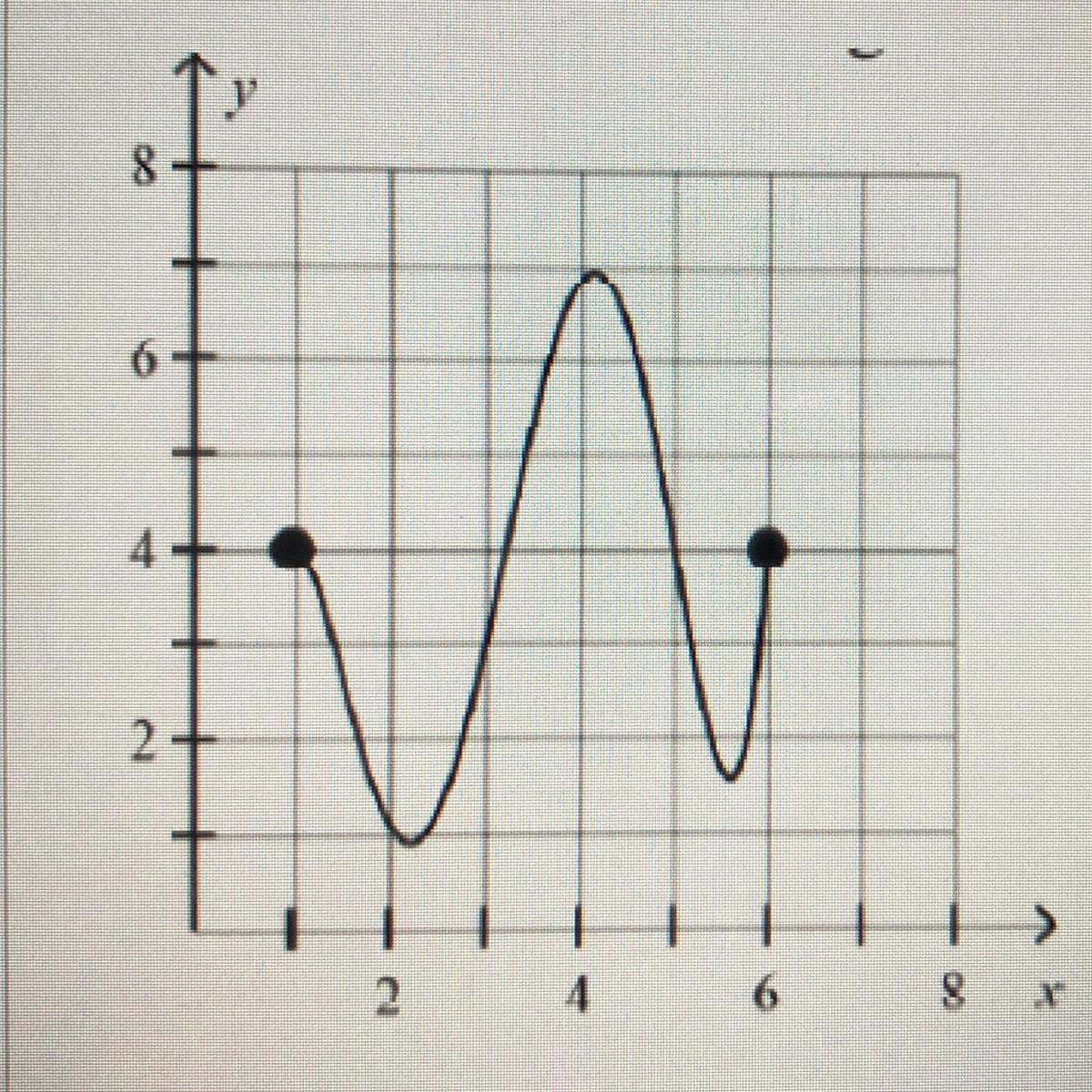
Answers
Answer:
Domain: 1, 6
Range: 4
Step-by-step explanation:
The Domain is the first coordinate which is x
The Range is the second coordinate which is y
The domain is the set of departure of a function into constrained to fall it is the sex X in the notation f:X-Y and is denoted as dom. The range is set of data is the diffrence between largest and smallest values so The domain is 1,6 and range is 4
-1 5/6p + 1 = 2 2/9
THIS IS AN EMERGENCY HELP
Answers
1 = 6/6 = 9/9
2 2/9 = 18/9 + 2/9 = 20/9
-11/6p + 9/9 = 20/9
-11/6p = 20/9 - 9/9
-11/6p = 11/9
p = 11/9 / -11/6
p = -6/9 = -2/3
For each 3 mm of coloured fabric Alex uses to make his curtains, he also uses 2 cm of white
fabric. Express the amount of white fabric to coloured fabric as a ratio in its simplest form.
PLEASE I NEED HELP. XXXXX
Answers
Answer: 20:3
Step-by-step explanation:
=) 2 cm = 20 mm
therefore, 20:3
Chapter 11- Probability Calculating Probability In an experiment an 8 sided die is tossed: a) Write down the sample space for this experiment.
Answers
The sample space for the probability calculation in an experiment with 8 sided die is {1,2,3,4,5,6,7,8}
As per the question statement, we are supposed to find the sample space for the probability calculation in an experiment with 8 sided die.
Before solving it, we need to know about Sample space. It is a collection of all the possible outcomes of an experiment and written in a set form.
In a 8 sided die, number of possible outcomes = 8
Outcomes can be 1, 2, 3, 4, 5, 6, 7 or 8
Therefore sample space = {1,2,3,4,5,6,7,8}
Sample space : It is a set and collection of all the possible outcomes and results of an experiment in a set form.To learn more about this topic, click on the link given below:
https://brainly.com/question/28043513
#SPJ9
a bag contains 6 red, 8 white, and 5 blue marbles. find the probability of picking 3 red marbles if each marble is returned to the bag before the next marble is picked.
Answers
The probability of randomly picking 3 red marbles in a row is:
P = 0.0315
How to find the probability?If all the marbles have the same probability of being randomly selected, then the probability of selecting at random a red marble is equal to the quotient between the number of red marbles and the total number of marbles in the bag.
There are 6red ones and (6 + 8 + 5 = 19) 19 marbles in total, then the probability is:
P = 6/19
And we want to do this thing 3 time (when we get the red marble we return it to the bag).
Then we will have the probabilities:
q = 6/19
k = 6/19
The joint probability of these 3 events is the product between the individual probabilities, we will get:
P = (6/19)*(6/19)*(6/19) = 0.0315
Learn more about probability at:
https://brainly.com/question/25870256
#SPJ1
What is the slope of the line that passes through the points (6, -5)(6,−5) and (6, -4)(6,−4)? Write your answer in simplest form.
Answers
When graphed, one point is on top of the other, creating a vertical line. This could either be ∞ or -∞ .
What is the value of x in the equation Three-fourths (one-fourth x + 8) minus (one-half x + 2) = StartFraction 3 Over 8 EndFraction (4 minus x) minus one-fourth?
Answers
Answer:
x=-44
Step-by-step explanation:
3/4(1/4x+8)-(1/2x+2)=3/8(4-x)-1/4
3/16x+24/4-1/2x-2=12/8-3/8x-1/4
3/16x+6-1/2x-2=3/2-3/8x-1/4
3/16x-1/2x+4=3/2-3/8x-1/4
-5/16x+4=-3/8x+5/4
Add 3/8x to both sides
-5/16x+4+3/8x=-3/8x+5/4+3/8x
1/16x+4=5/4
Subtract 4 from both sides
1/16x+4-4=5/4-4
1/16x=-11/4
Multiply both sides by 16
1/16x(16)=-11/4(16)
x=-44
Answer:
-8
Step-by-step explanation:
I just took it on edge.
8. Probability & Statistics: Brownian motion If we have a Brownian motion, Xt, X0 = 0, X1 > 0, what is the probability of X2 < 0 ?
a. 0
b. ½
c. 1/3
d. ¼
Answers
The correct option is d. ¼, which is the probability of the particle having a negative displacement at time t = 2 if there is Brownian movement.
In this problem, we are given a Brownian motion with X0 = 0 and X1 > 0, and we need to find the probability of X2 < 0.
We can use the properties of Brownian motion to solve this problem. Since X1 > 0, we know that the particle has moved to the right of the origin at time t = 1. Since the process has independent and stationary increments, we can assume that the particle moves from X1 to X2 in the same way as it moved from 0 to X1.
Therefore, the displacement of the particle from X1 to X2 is equivalent to the displacement of the particle from 0 to X1. Since X1 is positive, we know that the particle has a positive displacement at time t = 1.
The probability of the particle having a negative displacement at time t = 2 depends only on the variance of the Brownian motion over the time interval [1,2]. The variance of a Brownian motion over an interval of length t is proportional to t, so the variance of the displacement from X1 to X2 is twice the variance of the displacement from 0 to X1.
Therefore, the probability of X2 < 0 is given by the probability that a standard normal random variable is less than -X1/√2, since the variance of the displacement from X1 to X2 is twice the variance of the displacement from 0 to X1.
This probability can be calculated using a standard normal table or a calculator, and it is given by:
P(X2 < 0) = P(Z < -X1/√2) = 1 - Φ(X1/√2)
where Φ is the standard normal cumulative distribution function.
Substituting X1 = E[X1] = √1 = 1, we get:
P(X2 < 0) = 1 - Φ(1/√2) ≈ 0.25
Therefore, the correct option is d. ¼, which is the probability of the particle having a negative displacement at time t = 2.
Brownian motion is a stochastic process that models the random movement of particles in a fluid. It is a continuous-time process, where the change in position over a small time interval is normally distributed with mean zero and variance proportional to the length of the interval.
Know more about "probability" here:-
https://brainly.com/question/30298017#
#SPJ11
The perimeter of a square courtyard is 144 m. Find the cost of cementing it at the rate of £5 per m². *
Answers
Answer:
the cost is £ 6,480
Step-by-step explanation:
given:
The perimeter of a square courtyard is 144 m
find:
the cost of cementing it at the rate of £5 per m².
Perimeter = 4 Sides
144 = 4 S
S = 144/4
S = 36
Area = S²
A = 36²
A = 1296 m²
cost of cementing the area = 1296 m² x £5 per m² = £ 6,480
therefore,
the cost is £ 6,480
Tisha tried to evaluate an expression. Here is her work: 490÷729–23 = 490÷499–23 Step 1 = 109–23 Step 2 = 90–23 Step 3 = 883 Step 4 = 264 Step 5 Is Tisha's work correct?
Answers
Answer:
No, she made mistake from step 3, going to step 4
Step-by-step explanation:
See attachment for complete expression and Tisha's steps
Required
Is she correct?
The steps up to step 3 is correct.
However, going to step 4; she made a mistake
Her expression is:
Step 3: \(90 - 2 * 3\)
The correct step is to multiply 2 by 3 (using BODMAS)
This will give:
\(90 - 6\)
\(84\)
But instead she evaluated the subtraction first, which is incorrect.

find an equation of the curve that passes through the point (0, 1) and whose slope at (x, y) is 5xy. (note: start your answer with y
Answers
The equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is y = (5/2) * x^2y + 1. This equation represents a curve where the y-coordinate is a function of the x-coordinate, satisfying the conditions.
To determine an equation of the curve that satisfies the conditions, we can integrate the slope function with respect to x to obtain the equation of the curve. Let's proceed with the calculations:
We have:
Point: (0, 1)
Slope: 5xy
We can start by integrating the slope function to find the equation of the curve:
∫(dy/dx) dx = ∫(5xy) dx
Integrating both sides:
∫dy = ∫(5xy) dx
Integrating with respect to y on the left side gives us:
y = ∫(5xy) dx
To solve this integral, we treat y as a constant and integrate with respect to x:
y = 5∫(xy) dx
Using the power rule of integration, where the integral of x^n dx is (1/(n+1)) * x^(n+1), we integrate x with respect to x and get:
y = 5 * (1/2) * x^2y + C
Applying the initial condition (0, 1), we substitute x = 0 and y = 1 into the equation to find the value of the constant C:
1 = 5 * (1/2) * (0)^2 * 1 + C
1 = C
Therefore, the equation of the curve that passes through the point (0, 1) and has a slope of 5xy at any point (x, y) is:
y = 5 * (1/2) * x^2y + 1
Simplifying further, we have:
y = (5/2) * x^2y + 1
To know more about equation of the curve refer here:
https://brainly.com/question/31467851#
#SPJ11
A bottle contains many balls with different colors. Two balls arechosen without replacement. The probability of selecting agreen ball and then a white ball is 0.15, and the probability ofselecting a green ball on the first draw is 0.65. What is theprobability of selecting a white ball on the second draw, giventhat the first ball drawn was green?Enter your answer as a decimal rounded to the nearesthundredth.
Answers
We have to find the probability of selecting a white ball on the second draw given that the first ball drawn was green.
We know that probability of selecting a green ball and then a white ball without replacement is 0.15, so we can write:
\(P(G,W)=0.15\)We also know that the probability of selecting a green ball in the first draw is 0.65:
\(P(G)=0.65\)Then, we can use this to find the conditional probability of selecting a white ball on the second draw given that the first ball drawn was green can be calculated as:
\(P(W|G)=\frac{P(G,W)}{P(G)}=\frac{0.15}{0.65}\approx0.231\)Answer: the probability is 0.231.
How do solve 31 = 5 - 2(3x+4) - x. It can be a fraction.
Answers
first you distribute, then you combine like terms, then get x by itself and then divide but in this problem you keep it in a fraction.

an analysis of variance is used to evaluate the mean differences for a research study comparing three treatment conditions and the same number of scores in each sample. if ssbetween treatments
Answers
The analysis of variance (ANOVA) is a statistical method in a research study. The sum of squares between treatments (SSbetween) is a measure of the variability between the treatment conditions.
ANOVA breaks down the total variability in the data into different components to determine the sources of variation. SSbetween represents the variation between the treatment conditions and provides information about the differences among the means. By comparing the mean square between treatments (MSbetween) with the mean square within treatments (MSwithin), we can determine if the observed differences between the treatment conditions are statistically significant.
If SSbetween is relatively large compared to MSwithin, it suggests that the treatment conditions have a significant effect on the dependent variable. This means that the means of the treatment groups are significantly different from each other, indicating that the treatments are having an impact. On the other hand, if SSbetween is small compared to MSwithin, it suggests that the treatment conditions do not have a significant effect, and any differences observed between the treatment means may be due to random variation or chance.
In conclusion, the SSbetween in an ANOVA analysis provides valuable insights into the differences among treatment conditions in a research study. It helps determine if the observed mean differences are statistically significant, shedding light on the effectiveness or impact of different treatments.
Learn more about variation here:
https://brainly.com/question/29773899
#SPJ11
Nicholas is 5 feet 2 inches tall. On a sunny day he casts a shadow that is 3 feet long. At the same time, a nearby pole casts a shadow 15 feet 6 inches long. How tall is the pole?
Answers
Pole equation was 186-26= 160 and since a foot has 12 inches 160 divided by 12 is 13 feet and 4 inches
Find the surface area of the pyramid shown to the nearest whole number.
6ft 5ft 5ft
Answers
Answer:75,
Step-by-step explanation:
1/2 bh= A for one T 5*5=25 25*6= 150
150/2=75
OR
5*5/2=12.5
12.5*6=75
Find the first derivative for each of the following:
y = 3x2 + 5x + 10
y = 100200x + 7x
y = ln(9x4)
Answers
The first derivatives for the given functions are:
For \(y = 3x^2 + 5x + 10,\) the first derivative is dy/dx = 6x + 5.
For \(y = 100200x + 7x,\) the first derivative is dy/dx = 100207.
For \(y = ln(9x^4),\) the first derivative is dy/dx = 4/x.
To find the first derivative for each of the given functions, we'll use the power rule, constant rule, and chain rule as needed.
For the function\(y = 3x^2 + 5x + 10:\)
Taking the derivative term by term:
\(d/dx (3x^2) = 6x\)
d/dx (5x) = 5
d/dx (10) = 0
Therefore, the first derivative is:
dy/dx = 6x + 5
For the function y = 100200x + 7x:
Taking the derivative term by term:
d/dx (100200x) = 100200
d/dx (7x) = 7
Therefore, the first derivative is:
dy/dx = 100200 + 7 = 100207
For the function \(y = ln(9x^4):\)
Using the chain rule, the derivative of ln(u) is du/dx divided by u:
dy/dx = (1/u) \(\times\) du/dx
Let's differentiate the function using the chain rule:
\(u = 9x^4\)
\(du/dx = d/dx (9x^4) = 36x^3\)
Now, substitute the values back into the derivative formula:
\(dy/dx = (1/u) \times du/dx = (1/(9x^4)) \times (36x^3) = 36x^3 / (9x^4) = 4/x\)
Therefore, the first derivative is:
dy/dx = 4/x
To summarize:
For \(y = 3x^2 + 5x + 10,\) the first derivative is dy/dx = 6x + 5.
For y = 100200x + 7x, the first derivative is dy/dx = 100207.
For\(y = ln(9x^4),\) the first derivative is dy/dx = 4/x.
For similar question on derivatives.
https://brainly.com/question/31399608
#SPJ8
On coordinate plane point located at (- 1, - 2) and point K located at (8, 10) What is the distance, in units from point to point
Answers
Answer:
The answer would be 17
Step-by-step explanation:
Answer:
i belive your answer would be 8.5 units if i did the math correctly, im very sorry if thats wrong.
I hope this helps! :)
If f(x) = 4x + 2 and g(x) = x2 + 7, find each value:
1. f(4)
2. f(-2)
Answers
F(4)=4(4)+2=10
G(4)= (4)2+7=15
2. replace x by -2
F(x)=4(-2)+2= -6
G(x)= (-2)2+7= 3
Please give me brainliest!
i forgot how to do this can someone help.......
i need all four of them answered plz...

Answers
b. I don’t know
c. I also don’t know
d. I only knew the first one sorry
in a recent survey, what reason was given by nearly half of the respondents when asked what their reason was for changing jobs?
Answers
According to a recent survey, nearly half of the respondents cited better pay as their primary reason for changing jobs.
The survey was conducted on a national level and the results indicate that a majority of people are looking to increase their earnings by switching jobs.
Other reasons are:
The increasing cost of living and the desire to make ends meet. Opportunities to increase their skill set and gain experience in a new industry were other major factors that pushed them to seek a new job. Better working conditions were also cited as a primary reason by some survey respondents. This included working hours, location, job security, and organizational culture. To pursue a career path more aligned with their passions and interests. Move to a new location and a job change presented the perfect opportunity to do so.In conclusion, the survey clearly showed that the main reason for job changes among respondents was better pay. However, various other factors also play a role in an individual's decision to switch jobs, such as working conditions, career paths, and location.
To know more about changing jobs refer here:
https://brainly.com/question/20889936
#SPJ11
if the least-squares regression line for predicting y from x is y = 50 – 15x, what is the predicted value of y when x = 3?
Answers
The predicted value of y when x = 3, based on the least-squares regression line equation y = 50 - 15x, is y = 50 - 15(3) = 5.
The given least-squares regression line equation y = 50 - 15x represents a linear relationship between the variables x and y. In this equation, the coefficient of x (-15) represents the slope of the line, and the constant term (50) represents the y-intercept.
To find the predicted value of y when x = 3, we substitute x = 3 into the equation and solve for y. Plugging in x = 3, we have y = 50 - 15(3). Simplifying this expression, we get y = 50 - 45 = 5.
Therefore, when x = 3, the predicted value of y based on the least-squares regression line is 5. This means that according to the regression line, when x is 3, the expected or estimated value of y is 5.
Learn more about slope of the line here:
https://brainly.com/question/16180119
#SPJ11
2^x-2 + 2^3-x = 3
Solve for x
Answers
Answer:
The value of x is 3 or 2.
Step-by-step explanation:
Given equation is 2^(x-2) + 2^(3-x) = 3
On applying exponents rule a^(x-y) = a^x÷a^y
Where, a = 2, x = x and y = -2
a = 2, x = 3 and y = -xSo, using this, we get
⇛{(2^x/2²) + (2³/2^x)} = 3
⇛{(2^x/2*2) + {(2*2*2)/2^x}] = 3
⇛[(2^x)/4} + {(4*2)/2^x}] = 3
⇛[(2^x)/4} + {8/(2^x)}] = 3
Let assume that 2^x = y
So, above equation can be rewritten as
⇛{(y/4) + (8/y)} = 3
⇛{(y²+32)/4y} = 3
⇛{(y²+32)/4y} = (3/1)
On applying cross multiplication then
⇛1(y²+32) = 3(4y)
Multipy the number outside of the brackets with numbers and variables on the brackets on both LHS and RHS.
⇛y²+32 = 12y
⇛y²-12y + 32 = 0
By splitting the middle term, we get
⇛y² - 8y - 4y + 32 = 0
⇛y(y-8) - 4(y-8) = 0
⇛(y-8)(y-4) = 0
➝ y = 8 or y = 4
➝ 2^x = 8 or 2^x = 4
➝ 2^x = 2³ or 2^x = 2²
Therefore, x = 3 or x = 2
Answer: The value of x is 3 or 2.
VERIFICATION:
•If x = 3 the equation is
2^(x-2) + 2^(3-x) = 3
Substitute the value of x = 3 in equation
⇛2^(3-2) + 2^(3-3) = 3
⇛2¹ + 2⁰ = 3
⇛2 + 1 = 3
⇛3 = 3
LHS = RHS
•If x = 2 then the equation is
2^(x-2) + 2^(3-x) = 3
Substitute the value of x = 2 in equation
⇛2^(2-2) + 2^(3-2) = 3
⇛2^0 + 2^1 = 3
⇛1 + 2 = 3
⇛3 = 3
LHS = RHS
Hence, verified.
Please let me know if you have any other questions.
A scuba diver dove from the surface of the ocean to an elevation of −69 9/10
feet at a rate of −21.5 feet per minute. After spending 12.5 minutes at that elevation, the diver ascended to an elevation of −38 9/10
feet. The total time for the dive so far was 19 1/8
minutes. What was the rate of change in the diver's elevation during the ascent? Round your answer to the nearest hundredth.
Answers
The rate of change of the divers elevation = 19.274
Given,
The depth to which the Scuba dove = -69 \(\frac{9}{10}\) feet
The rate at which he dove = -21.5 feet per min.
The time which he spent at the elevation = 12.5min.
The elevation the diver then ascended to -38 \(\frac{9}{10}\) feet
Thee total time for the dove = 19 \(\frac{1}{8}\) minutes.
Therefore, the time \(t_{d}\) with which the scuba diver descended to -69 \(\frac{9}{10}\) feet
is given as follows:
\(t_{d} = \frac{Distance}{speed}\) = \(= \frac{-69\frac{9}{10} }{-21.5}= \frac{-681}{-21.5}\) = 3.167 minutes
The time \(t_{e}\), it took the scuba diver to elevate to -38 \(\frac{9}{10}\) feet is given as follows:
\(t_{e}\) = 19 \(\frac{1}{8}\)minutes - (3.167 + 10.5) minutes = 5.458 minutes
The rate of change of the divers elevation = (Final elevation - Initial elevation)/(Time taken).
∴ The rate of change of the divers elevation
= (-38 \(\frac{9}{10}\) - (-69 \(\frac{9}{10}\) )) / 5.458 min
=(37.1 - (-68.1))/ 5.458 min
= 19.274 feet/minutes to the nearest hundredth.
Hence, The rate of change of the divers elevation = 19.274
Learn more about Elevation at:
https://brainly.com/question/20305317
#SPJ1
A triangle has two sides of length 1 and 14. What is the largest possible whole-number length for the third side?
Answers
Answer:
14
Step-by-step explanation:
The triangle inequality is usually expressed as ...
a +b > c
for any permutation of a, b, c.
Here, that would mean ...
1 + 14 > c
c < 15
The largest whole-number value that the third side (c) can have is 14.
_____
Additional comments
Some authors write the triangle inequality as ...
a +b ≥ c
If you use that version, the longest side could be 15. Such a "triangle" would look like a line segment, and have zero area.
__
We can also check the shortest length:
c +1 > 14
c > 13
The smallest whole-number value for the shortest side is also 14. That is, the only triangle with whole-number side lengths of 1 and 14 will be an isosceles triangle with two sides of length 14.
