Answers
Related Questions
74. At the gym suppose that 10% of adults belong to health clubs, and 40% of these health club members go to the club at least twice a week. What percent of all adults go to a health club at least twice a week?
Write the information given in terms of probabilities,
and use the general multiplication rule.
Answers
The proportion of all adults go to a health club at least twice a week is 4%.
What is percent?
A percentage is a number or ratio expressed as a fraction of 100 in mathematics. Although the abbreviations "pct.", "pct.", and occasionally "pc" are also used, the percent sign, "%," is frequently used to indicate it. A percentage is a number without dimensions and without a standard measurement.
Given:
At the gym suppose that 10% of adults belong to health clubs, and 40% of these health club members go to the club at least twice a week.
The proportion of adults who belong to health clubs is 10% that is 0.10.
The proportion of these adults (health club members) go to the club at least twice a week is 40%, that is 0.40.
Hence, the proportion of all adults go to a health club at least twice a week is
0.10 × 0.40 = 0.04, that is 4%
To know more about percent, click on the link
https://brainly.com/question/14450597
#SPJ1
Perform the integral given: ∭(cos(3x)+e2y−sec(5z))dzdydx
Answers
The integral of ∭(cos(3x) + e^(2y) - sec(5z)) dz dy dx is z[(sin(3x)/3) y + (e\(^(2y)/2\)) y - y ln|sec(5z) + tan(5z)|] + C3.
To perform the integral ∭(cos(3x) + e^(2y) - sec(5z)) dz dy dx, we integrate with respect to z first, then y, and finally x. Let's go step by step:
Integrating with respect to z:
∫(cos(3x) + e^(2y) - sec(5z)) dz = z(cos(3x) + e^(2y) - ln|sec(5z) + tan(5z)|) + C1,
where C1 is the constant of integration.
Now, we have: ∫[z(cos(3x) + e^(2y) - ln|sec(5z) + tan(5z)|)] dy dx.
Integrating with respect to y:
∫[z(cos(3x) + e^(2y) - ln|sec(5z) + tan(5z)|)] dy = z(cos(3x)y + e\(^(2y)y\) - y ln|sec(5z) + tan(5z)|) + C2,
where C2 is the constant of integration.
Finally, we have:
∫[z(cos(3x)y + e\(^(2y)y\) - y ln|sec(5z) + tan(5z)|)] dx.
Integrating with respect to x:
∫[z(cos(3x)y + e\(^(2y)y\) - y ln|sec(5z) + tan(5z)|)] dx = z[(sin(3x)/3) y + (\(e^(2y)/2\)) y - y ln|sec(5z) + tan(5z)|] + C3,
where C3 is the constant of integration.
Therefore, the final result of the integral is z[(sin(3x)/3) y + (e\(^(2y)/2\)) y - y ln|sec(5z) + tan(5z)|] + C3.
LEARN MORE ABOUT integral here: brainly.com/question/31433890
#SPJ11
which number is divisible by both 2 and 4?a.1,022b.1,974c.2,836d.2,918
Answers
The number that is divisible by both 2 and 4 is option c. 2,836.
To determine which number is divisible by both 2 and 4, we need to identify the number that is divisible by the prime factorization of both 2 and 4.
Divisibility by 2To be divisible by 2, a number must be even, meaning it should end with 0, 2, 4, 6, or 8. Looking at the given options, we can eliminate options a. 1,022 and d. 2,918 because they end with 2 and 8 respectively.
Divisibility by 4To be divisible by 4, a number must be divisible by 2 twice. In other words, the last two digits of the number should form a multiple of 4. Examining the remaining options b. 1,974 and c. 2,836, we find that only option c. 2,836 satisfies this condition. The last two digits of 2,836, 36, form a multiple of 4 (9 times 4 is 36).
Therefore, the number 2,836 is divisible by both 2 and 4, hence the correct answer is: c.2,836
Learn more about Divisible
brainly.com/question/2273245
#SPJ11
What is the length of the hypotenuse?If necessary,round to the nearest tenth

Answers
Work Shown:
\(a^2 + b^2 = c^2\\\\40^2 + 75^2 = c^2\\\\1600 + 5625 = c^2\\\\7225 = c^2\\\\c^2 = 7225\\\\c = \sqrt{7225}\\\\c = 85\\\\\)
I used the pythagorean theorem with a = 40 and b = 75. The order of the 'a' and b doesn't matter, as long as c is the largest side.
The 40-75-85 pythagorean triple is the scaled up version of the 8-15-17 triple (multiply each piece by 5).
Answer:
85 yd
Step-by-step explanation:
We know that
\(\pmb{\bf H^2=P^2+B^2}\)
Here,
H = c, P = 75 yd, B = 40 yd
\( \begin{gathered} \: \sf \implies \: {c }^{2} = (75) {}^{2} + {(40)}^{2} \\ \sf \implies {c}^{2} = 5625 + 1600 \\ \sf \implies \: {c}^{2} = 7225 \\ \sf \implies \: c = \sqrt{7225} \\ \sf \implies \: c = 85 \: yd \end{gathered}\)
16. Audrey bought 4 yards of red fabric
, 2 yards of white, and 1 yards of blue. What is the
total amount of yards that she purchased?
Answers
Answer:
Audrey bought 7 yards.
Step-by-step explanation:
Just add 4+2+1 because those are what colors she bought, but all together she bought 7 yards of all colors.
true or false: linearity is justified if the residuals are randomly dispersed across the values of a predictor variable.
Answers
Answer: False
Step-by-step explanation: False. Linearity is a property of a mathematical model or equation, not of the residuals of that model. In general, the residuals of a model should be randomly dispersed across the values of a predictor variable if the model is a good fit for the data, but this is not a justification for linearity. Linearity refers to the relationship between the predictor and response variables in a model, and whether that relationship can be adequately represented by a straight line.
both methods requires two initial guesses x1 and x2, and it is necessary that f(x1)*f(x2) < 0
Answers
The requirement f(x1) * f(x2) < 0 for choosing initial guesses x1 and x2 with opposite signs ensures the validity and convergence of certain numerical root-finding methods such as the bisection method or the regula falsi method.
The statement you provided is true for certain numerical methods used to find roots of equations, such as the bisection method or the regula falsi method. These methods are iterative and require an initial interval or range where the root is expected to be found. To ensure convergence and a valid solution, it is necessary to choose initial guesses x1 and x2 such that the function f(x) evaluated at those points have opposite signs, i.e., f(x1) * f(x2) < 0.
The rationale behind this requirement is based on the Intermediate Value Theorem, which states that if a continuous function f(x) changes sign over an interval [x1, x2], then there exists at least one root within that interval. By ensuring that f(x1) and f(x2) have opposite signs, we guarantee the existence of a root within the interval [x1, x2].
The bisection method works by repeatedly bisecting the interval and selecting a new subinterval that contains the root. At each iteration, the method narrows down the interval by halving it, based on the sign change observed in the function evaluations.
Similarly, the regula falsi (or false position) method also operates by iteratively refining the interval based on the linear interpolation between the function values at the endpoints. The method adjusts the interval based on the sign change of the function, converging to the root.
Both methods rely on the property of opposite signs to guarantee convergence and avoid getting stuck in a non-converging or incorrect solution. If the initial guesses do not satisfy the condition f(x1) * f(x2) < 0, it is possible that the method fails to converge or converges to a different root or solution.
Learn more about bisection method at: brainly.com/question/30320227
#SPJ11
Describe the transformation:
A-Translation, 2 units down
B-Reflection across y-axis
C-Reflection across y=x
D-Reflection across x-axis
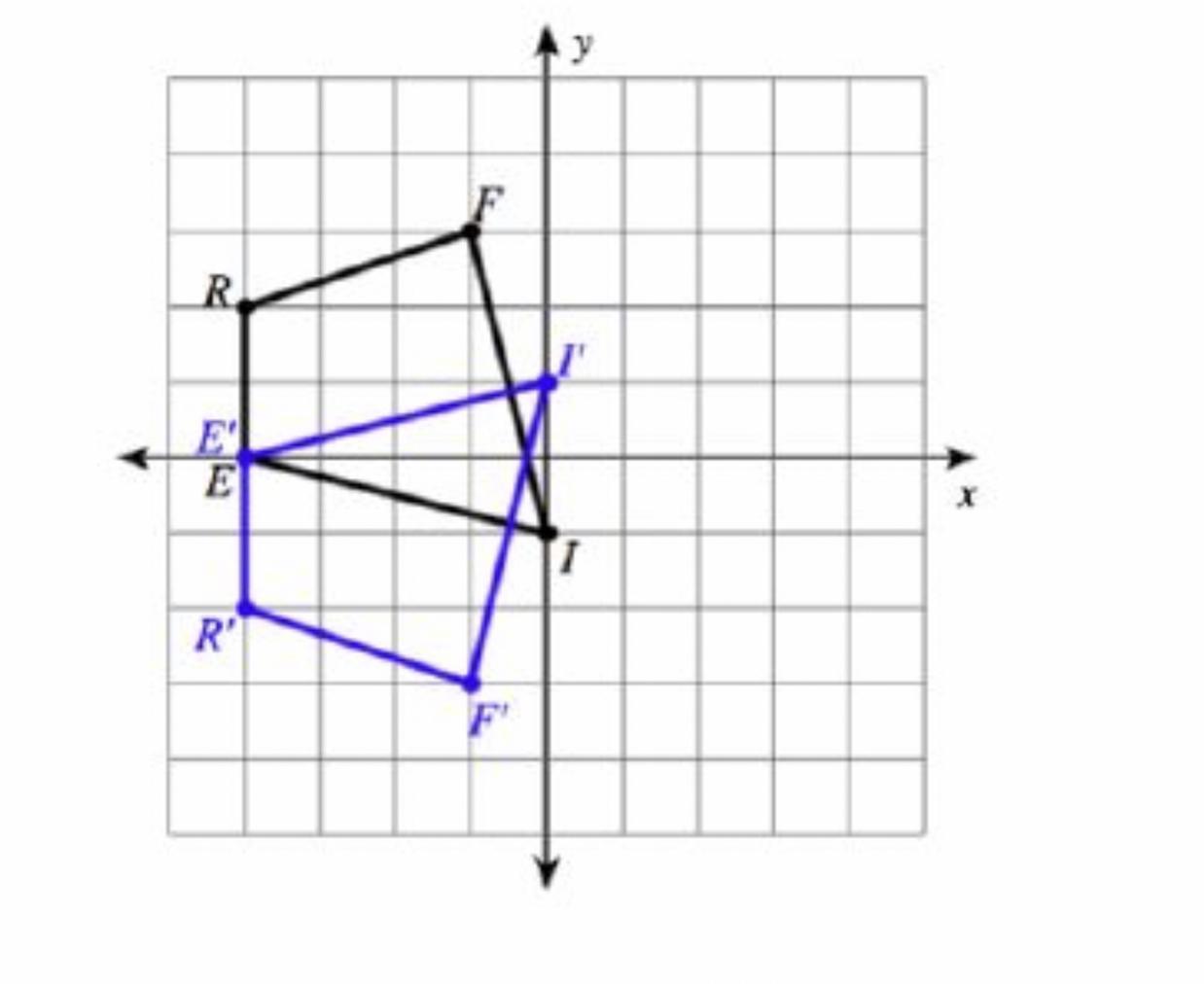
Answers
Answer:
D-Reflection across x-axis
I NEED HELP. Find the Values of a,b, que and v

Answers
Answer:
a=118
b=64
q=84
v=84
Step-by-step explanation:
b=62
a=18-=b
a=180-62
a=118
q=180-s or r
q=180-96
q=84
v=q
v=84
Which of the following is correct for determining the length of x to the nearest tenth of a metre?
cos 42 = x/6
tan 48 = x/5
sin 48 = x/5
tan 42 =x/6

Answers
The lifetime of a product can be estimated using a normal distribution. What is the probability that the product will last between 16.536 and 8.054 years if the average lifetime has a mean of 14.242 years and a standard deviation of 3.978 years?
Answers
The to your question is that we can use the normal distribution to estimate the probability that the product will last between 16.536 and 8.054 years.
In this case, we want to calculate the probability for x = 16.536 and x = 8.054. The mean (μ) is 14.242 years, and the standard deviation (σ) is 3.978 years.
Using the formula, we can calculate the z-scores for both values:
For x = 16.536: z = (16.536 - 14.242) / 3.978
For x = 8.054: z = (8.054 - 14.242) / 3.978
Once we have the z-scores, we can look up the corresponding probabilities in the standard normal distribution table or use a calculator. Subtracting the probability for the lower z-score from the probability for the higher z-score will give us the probability that the product will last between 16.536 and 8.054 years.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
"I am thinking of a number. If you
multiply my number by 4 and then add 3
times my number, you will get 175. What is
my number?"
Answers
Answer:
y =25Step-by-step explanation:
y×4+3×y=175 4y+3y=175 7y=175 divide by 7 both side with make value of y y=25. this is my answerWhat evidence is needed to prove two triangles are similar by the SSS similarity theorem?
Answers
Consider the same figure as given above. It is observed that DP/PE = DQ/QF and also in the triangle DEF, the line PQ is parallel to the line EF.
So, ∠P = ∠E and ∠Q = ∠F.
Hence, we can write: DP/DE = DQ/DF= PQ/EF.
The above expression is written as
DP/DE = DQ/DF=BC/EF.
It means that PQ = BC.
Hence, the triangle ABC is congruent to the triangle DPQ.
(i.e) ∆ ABC ≅ ∆ DPQ.
Thus, by using the AAA criterion for similarity of the triangle, we can say that
∠A = ∠D, ∠B = ∠E and ∠C = ∠F.
To know more about triangle check the below link:
https://brainly.com/question/1058720
#SPJ4
PLS HELP DUE IN 15-20 MINS!!

Answers
The negation of the product of five times a number divided by two is ten?
Answers
The algebraic expression that can be represented by the statement is -5x/2 = 10
How to make a algebraic expression that can be represented by the statement?From the question, we have the following statement that can be used in our computation:
The negation of the product of five times a number divided by two is ten
Represent the variable with y
So, we have the following representation
The negation of the product of five times x divided by two is ten
Express the product as an actual product
So, we have the following representation
The negation of 5x divided by two is ten
Express the quotient as an actual quotient
So, we have the following representation
The negation of the 5x/2 is ten
Lastly, we have
-5x/2 = 10
Hence, the expression is -5x/2 = 10
Read more about word problems at
brainly.com/question/21405634
#SPJ1
What is the distance between the points (2, -7) and (-3, -2) on the coordinate plane?
Answers

Use the Pythagorean Theorem to write an equation to find the mission side of the triangle, then find the missing side. Round final answer to the nearest hundredth if necessary.

Answers
Answer:
x ≈ 5.50
Step-by-step explanation:
\(x^2=11.7^2-10.3^2\)
\(x^2=30.8\)
\(x=\sqrt{30.8}\)
\(x=5.4977477\)
x ≈ 5.50
Answer:
\( \boxed{\sf x \approx 5.50} \)
Step-by-step explanation:
According to Pythagoras Theorem, "In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides"
\( \therefore \\ \sf \implies x^{2} + 10.3^{2} = 11.7^{2} \\ \\ \sf 10.3 ^{2} = 106.09: \\ \sf \implies {x}^{2} + \boxed{106.09} = 11.7^{2} \\ \\ \sf 11.7^{2} = 138.89: \\ \sf \implies {x}^{2} + 106.09 = \boxed{138.89} \\ \\ \sf Subtracting \ 106.09 \ from \ both \ sides: \\ \sf \implies {x}^{2} = 138.89 - 106.09 \\ \\ \sf 138.89 - 106.09 = 30.8 \\ \sf \implies {x}^{2} = \boxed{30.8} \\ \\ \sf Taking \ square \ root \ of \ both \ sides: \\ \sf \implies x = \sqrt{30.8} \\ \\ \sqrt{30.8} = 5.5497: \\ \sf \implies x = \boxed{5.5497} \\ \\ \sf \implies x \approx 5.50 \)
Y-(5-(y-x)) x = 4 y = 6
I need the steps please, this is a little bit confusing..
Answers
Answer:
3
Step-by-step explanation:
substitute x = 4 , y = 6 into the expression
y - (5 - (x - y))
= 6 - (5 - (6 - 4))
= 6 - (5 - 2))
= 6 - 3
= 3
X + 3 + 7 (X-5) Step by step
Answers
Answer: 8x - 32
Step-by-step explanation: x + 3 + 7(x - 5)
x + 3 - 35
which gives you 8x - 32
A hemisphere bowl is made of brass,0. 25cm thickness the inner radius of the bowl is 5cm find the ratio of outer surface area to inner surface area
Answers
With the information of hemisphere bowl, The ratio of outer surface area to inner surface area is approximately 1.385
The inner surface area of the hemisphere bowl can be calculated as follows:
A = 2 x π x r²
where r is the radius of the hemisphere, which is 5cm.
So, the inner surface area is:
A = 2 x π x 5² = 2 x π x 25 = 50π cm²
The outer surface area of the hemisphere bowl can be calculated by finding the surface area of a full sphere with the same radius and subtracting the surface area of the inner part of the bowl.
The surface area of a sphere can be calculated as:
A = 4 x π x r²
where r is the radius of the sphere, which is 5cm + 0.25cm (the thickness of the bowl).
So, the surface area of the full sphere is:
A = 4 x π x (5 + 0.25)^2 = 4 x π x (5.25)² = 138.5π cm²
The outer surface area of the hemisphere bowl is half the surface area of a full sphere, which is 138.5π / 2 = 69.25π cm²
Finally, the ratio of outer surface area to inner surface area is:
69.25π / 50π = 1.385
So, the ratio of outer surface area to inner surface area is approximately 1.385.
To learn more about inner surface area click here:
brainly.com/question/19577114
#SPJ4
Consider a 1-D harmonic oscillator and a trial wavefunction of the form ψ(x)=A/(x^2 + α^(2)), [20] where A is the normalization constant and α is an adjustable parameter. (a) Determine A. [3] (b) Estimate the ground-state energy of the harmonic oscillator. [12] (c) Check whether ⟨H⟩ overestimates or underestimates the solution you obtained in 3(b), and hence describe the validity of the variational principle in this case. [5]
Answers
a.we get, `A = √(2α³/π)`.
b.`⟨H⟩ = (3/4)hω - (h²/4ma²)` where `a = α/√(mω/h)`.
c.we can say that the variational principle is valid in this case.
(a) Let's find the normalization constant A.
We know that the integral over all space of the absolute square of the wave function is equal to 1, which is the requirement for normalization. `∫⟨ψ|ψ⟩dx= 1`
Hence, using the given trial wavefunction, we get, `∫⟨ψ|ψ⟩dx = ∫ |A/(x^2+α²)|²dx= A² ∫ dx / (x²+α²)²`
Using a substitution `x = α tan θ`, we get, `dx = α sec² θ dθ`
Substituting these in the above integral, we get, `A² ∫ dθ/α² sec^4 θ = A²/(α³) ∫ cos^4 θ dθ`
Using the identity, `cos² θ = (1 + cos2θ)/2`twice, we can write,
`A²/(α³) ∫ (1 + cos2θ)²/16 d(2θ) = A²/(α³) [θ/8 + sin 2θ/32 + (1/4)sin4θ/16]`
We need to evaluate this between `0` and `π/2`. Hence, `θ = 0` and `θ = π/2` limits.
Using these limits, we get,`⟨ψ|ψ⟩ = A²/(α³) [π/16 + (1/8)] = 1`
Therefore, we get, `A = √(2α³/π)`.
Hence, we can now write the wavefunction as `ψ(x) = √(2α³/π)/(x²+α²)`.
(b) Using the wave function found in part (a), we can now determine the expectation value of energy using the time-independent Schrödinger equation, `Hψ = Eψ`. We can write, `H = (p²/2m) + (1/2)mω²x²`.
The first term represents the kinetic energy of the particle and the second term represents the potential energy.
We can write the first term in terms of the momentum operator `p`.We know that `p = -ih(∂/∂x)`Hence, we get, `p² = -h²(∂²/∂x²)`Using this, we can now write, `H = -(h²/2m) (∂²/∂x²) + (1/2)mω²x²`
The expectation value of energy can be obtained by taking the integral, `⟨H⟩ = ⟨ψ|H|ψ⟩ = ∫ψ* H ψ dx`Plugging in the expressions for `H` and `ψ`, we get, `⟨H⟩ = - (h²/2m) ∫ψ*(∂²/∂x²)ψ dx + (1/2)mω² ∫ ψ* x² ψ dx`Evaluating these two integrals, we get, `⟨H⟩ = (3/4)hω - (h²/4ma²)` where `a = α/√(mω/h)`.
(c) Since we have an approximate ground state wavefunction, we can expect that the expectation value of energy ⟨H⟩ should be greater than the true ground state energy.
Hence, the value obtained in part (b) should be greater than the true ground state energy obtained by solving the Schrödinger equation exactly.
Therefore, we can say that the variational principle is valid in this case.
To know more about time-independent Schrödinger equation,visit:
https://brainly.com/question/31642338
#SPJ11
Find the area of the figure.
2 cm
3 cm
6 cm
12 cm

Answers
Answer:
66 cm^2
Step-by-step explanation:
12*6=72 cm^2 and to find the missing pience of the rectangle you multiply 3*2= 6 cm^2.
72 - 6 = 66
An ice cream tore ell 3 drink, in 5 ize, and 6 flavor. In how many way can a cutomer order a drink?
Answers
Total number of ways in which a customer can order a unique drink is 90
The number of drinks= 3
The number of Size= 5
The number of Flavors = 6
Using the formula of combination from permutation and combination
ₙ\(C_{r}\)= n!/r!(n-r)!
where,
n= total number of objects
r= number of selected objects
and n!= n factorial
where factorial is: n!= nx(n-1)x(n-2)x......x3x2x1
for eg. 4!=4X3X2X1 = 24
we use combination here instead of permutation as the order in which the choices are made is not important.
ₙ\(C_{r}\)= n!/r!(n-r)!
ₙ\(C_{r}\)= 3!x5!x6!/1!(3-1)!(5-1)!(6-1)!
ₙ\(C_{r}\)= 3!x5!x6!/2!x4!x5!
ₙ\(C_{r}\)= 3 x 2! x 5 x4! x 6 x 5!/2!x4!x5!
ₙ\(C_{r}\)= 3x5x6
ₙ\(C_{r}\)= 90
It can also be understood as:
Let the total number of ways in which a customer can order a drink be c
The first choice that the customer makes in the drink, as there are 3 types of drinks, c=1x3 (where 1 is the number of ways selected)
The next choice to be made is the size of the drink, as there are 5 sizes, c=3x5=15
c=15
The last choice is the flavor of the drink, the given question has 6 flavors, so, c=3x5x6
c=3x5x6
c=15x6
c=90
Learn more about Permutation and Combination at:
brainly.com/question/28720645
#SPJ4
If we have an effect, would error variance go away?
Answers
No, the presence of an effect does not necessarily imply that error variance will go away.
Why could not error variance go away?The presence of an effect does not necessarily imply that error variance will go away. In fact, error variance is an inherent part of any statistical model and represents the amount of variation in the response variable that is not explained by the predictor variables.
Even if a predictor variable has a significant effect on the response variable, there may still be some unexplained variation in the response that is attributable to error variance.
It is important to take into account and control for error variance in any statistical analysis, as it can affect the precision and accuracy of the estimates of the model parameters and can also influence the interpretation of the results.
One way to control for error variance is to use appropriate statistical methods, such as analysis of variance (ANOVA), regression analysis, or other modeling techniques that take into account the variability in the data.
Learn more about error variance
brainly.com/question/31592090
#SPJ11
Find the slope of the line

Answers
Answer:
1/2
Step-by-step explanation:
Pick two points on the line
I picked (0, 2) and (2, 3)
m = (3-2)/(2 -0) = 1/2
In Rebecca's neighborhood, 85% of the houses have garages and 34% have a garage and a pool. What is the probability (in percent) that a house in her neighborhood has a pool, given that it has a garage? Round your answer to 1 decimal place
Answers
Given that 85% of the houses have garages and 34% have a garage and a pool, we can use conditional probability to determine the probability that a house in Rebecca's neighborhood has a pool, given that it has a garage. Conditional probability is the probability of an event given that another event has occurred.
Mathematically, conditional probability is given by the formula:P(A|B) = P(A and B) / P(B), where A and B are two events. P(A|B) represents the probability of A given B. P(A and B) represents the probability of A and B occurring together. P(B) represents the probability of B.Let's assume that A represents the event of having a pool, and B represents the event of having a garage. We are interested in finding the probability of having a pool given that a house has a garage. We can represent this mathematically as:P(A|B) = P(A and B) / P(B)We know that 34% of the houses have a garage and a pool. This means that P(A and B) = 0.34.We also know that 85% of the houses have garages. This means that P(B) = 0.85.Substituting these values into the conditional probability formula:P(A|B) = 0.34 / 0.85 = 0.4 = 40%Therefore, the probability that a house in Rebecca's neighborhood has a pool, given that it has a garage, is 40%. Rounded to one decimal place, the answer is 40.0%.For such more question on probability
https://brainly.com/question/30390037
#SPJ8
A container built for transatlantic shipping is constructed in the shape of a right rectangular prism. Its dimensions are 10.5 ft by 7 ft by 10 ft. If the container is entirely full and, on average, its contents weigh 0.24 pounds per cubic foot, find the total weight of the contents. Round your answer to the nearest pound if necessary.
Answers
Answer: 3062 pounds
Step-by-step explanation: 10.5x7x10 is 735 and divided by 0.24 is 3062.2 pounds rounded to 3062
Use the diagram below to answer questions 1-3. 60 C b If a=5, then the value of b is 2.9 8.7 C 17.3 D 5.8 2. If C= 10. then the exact value of b is B 5 с A 5.8 D 17.3 3. If b=7, then the value of a is 3.5 С 14 12.1 A B 4.04

Answers
Answer:
1. A
2. B
3. D
Sort of explanation:
This is a 30° 60° 90° triangle, so the rules below apply:
x is the short leg of the triangle, located across from the 30° angle. (In this problem, the short leg is labled b)
The hypotenuse leg is across from the right angle, and is always 2x (In this problem, the hypotenuse leg is labled c)
The long leg of the triangle is located across the 60° angle and is always x√3. (in this problem, the long leg is labeled a)
below the paraboloid z = 18 − 2x2 − 2y2 and above the xy-plane
Answers
Answer:
y
2
=−
2
z
+7
Steps for Solving Linear Equation
z=18−2×2−2y2
Multiply 2 and 2 to get 4.
z=18−4−2y
2
Subtract 4 from 18 to get 14.
z=14−2y
2
Swap sides so that all variable terms are on the left hand side.
14−2y
2
=z
Subtract 14 from both sides.
−2y
2
=z−14
Divide both sides by −2.
−2
−2y
2
=
−2
z−14
Dividing by −2 undoes the multiplication by −2.
y
2
=
−2
z−14
Divide z−14 by −2.
y
2
=−
2
z
+7
Step-by-step explanation:
the given equation defines a paraboloid that lies below the plane z=0. Specifically, it is situated above the xy-plane, which means that the z-values of all points on the surface are greater than or equal to zero.
we can break down the equation z=18-2x^2-2y^2. This equation represents a paraboloid with its vertex at (0,0,18) and axis of symmetry along the z-axis. The first term 18 is the z-coordinate of the vertex and the last two terms -2x^2 and -2y^2 determine the shape of the paraboloid.
Since the coefficient of x^2 and y^2 terms are negative, the paraboloid is downward facing and opens along the negative z-axis. Therefore, all points on the paraboloid have z-values less than 18. Additionally, since the paraboloid is situated above the xy-plane, its z-values are greater than or equal to zero.
the paraboloid defined by the equation z=18-2x^2-2y^2 is situated below the plane z=0 and above the xy-plane. Its vertex is at (0,0,18) and it opens along the negative z-axis.
To know more about paraboloid, visit:
https://brainly.com/question/30925041
#SPJ11
An airplane travels at a constant speed of 540 miles per hour. How far, in
miles, will the
airplane travel in 20 minutes?

Answers
Answer:
27
Step-by-step explanation:
540/20=27
