Answers
The measure of the missing angle a is 155 degrees.
What is the measure of the missing angle?The sum of angles on a straight line is equal to 180 degrees.
From the diagram;
Supplement angle to a = 25°Angle a = ?Since the sum of angles on a straight line is equal to 180 degrees.
Supplement angle to a + angle a = 180
25° + a = 180°
Solve for a by subtracting 25° from both sides.
25° - 25° + a = 180° - 25°
a = 180° - 25°
a = 155°
Therefore, the measure of angle a is 155°.
Learn more about supplementary angles here: https://brainly.com/question/18164299
#SPJ1
Related Questions
Determine if certain size requirements are met to use the normal distribution. The probability that at least 92 people recognize McDonald's brand name, the probability of a random person doing so is 95%
Answers
Yes, the normal distribution can be used to approximate the probability of at least 92 people.
How to determine size of normal distribution?To determine if the normal distribution can be used to solve this problem, we need to check if the sample size is sufficiently large and if the sample proportion is not too close to 0 or 1.
The sample size is not given in the problem statement, but we can assume that it is large enough for the normal distribution to be a reasonable approximation. A general rule of thumb is that the normal distribution can be used if the sample size is at least 30.
The problem states that the probability of a random person recognizing the McDonald's brand name is 0.95. We can interpret this as the sample proportion (p-hat) being equal to 0.95. The normal distribution can be used to approximate the probability of at least 92 people recognizing the brand name if the following conditions are met:
np >= 10, where n is the sample size and p is the population proportion (or the estimated sample proportion if the population proportion is unknown). In this case, we can assume that the population proportion is equal to the sample proportion, so np = n(0.95) >= 10. As long as the sample size is large enough, this condition should be met.n(1-p) >= 10. This condition is also known as the "success-failure" condition, and it ensures that both the number of "successes" (in this case, people who recognize the brand name) and the number of "failures" (people who do not recognize the brand name) are sufficiently large. In this case, n(1-0.95) = 0.05n >= 10. As long as the sample size is large enough, this condition should also be met.Since we can assume that the sample size is large enough, and both np >= 10 and n(1-p) >= 10, we can use the normal distribution to approximate the probability of at least 92 people recognizing the McDonald's brand name.
Learn more about Normal distribution
brainly.com/question/14012161
#SPJ11
2. Choose 3 integers less than or equal to 8?
a). x = 8,9,10
b). x =-3,0,10
c), x = 0,1,8
d) x = 2,3,9
Answers
Answer:
c
Step-by-step explanation:
because 8 is equal to 8. 0 and 1 are less than 8.
10. Find the parallel slope: (-2.9) and (1.-3).
Answers
What is the fraction to this equation 0.020
Pls help fast.
Answers
Answer: 1/50
Step-by-step explanation:
0.020 = 20/1000 = 1/50
According to the graph, what is the experimental probability of selecting tho color yellow
35%
14%
20%
88%

Answers
Answer:
35%
Step-by-step explanation:
The number of yellow is 35% of the total items.
Find the cost of 2 1/2 metres of cloth at 47 5/4 rupee per metre.
Answers
Answer:
Therefore, the cost of 2 1/2 metres of cloth at 47 5/4 rupee per metre is 955/8 rupee.
Step-by-step explanation:
We can solve this problem using multiplication and addition as follows:
The cost of 1 metre of cloth is 47 5/4 rupee.
So, the cost of 2 1/2 metres of cloth is:
2 1/2 * 47 5/4
To multiply mixed numbers, we first convert them to improper fractions.
2 1/2 = 5/2
47 5/4 = 191/4
So, 2 1/2 * 47 5/4 = 5/2 * 191/4
To multiply fractions, we multiply the numerators together and the denominators together.
5/2 * 191/4 = (5 * 191)/(2 * 4) = 955/8
Therefore, the cost of 2 1/2 metres of cloth at 47 5/4 rupee per metre is 955/8 rupee.
y=225(1.23)^2
growth or decay
Answers
Answer:
Growth
Step-by-step explanation:
You can simply look at this and say that this is growth because the number in the parenthesis is greater than 1.00.
It would only be decay if the parenthesis^2 resulted in a number less than 1
if a figure can be rotated 360° to be mapped onto itself, is it considered to have rotational symmetry? explain.
Answers
Yes, if a figure can be rotated 360° to be mapped onto itself, it is considered to have rotational symmetry.
This is because a 360° rotation means that the figure will return to its original position, making it symmetrical. Rotational symmetry is a type of symmetry where a figure can be rotated about a central point and still look the same. The degree of rotational symmetry depends on the number of times a figure can be rotated to match its original appearance. Therefore, if a figure can be rotated 360° and maintain its original appearance, it is said to have rotational symmetry of degree 1. This is true regardless of the size, orientation, or position of the figure. Yes, a figure that can be rotated 360° to be mapped onto itself is considered to have rotational symmetry. Rotational symmetry occurs when an object can be rotated around a central point and still appear the same as its original position. In the case of a 360° rotation, the figure returns to its initial configuration, confirming its rotational symmetry.
To know more about symmetry visit:
https://brainly.com/question/29044130
#SPJ11
What inequality is on the number line?

Answers
y ≥ -5
Explanation:
y is greater than -5 because the darkened line is heading towards the positive side.
(The positives are greater than the negatives.)
(The smaller negative numbers are greater than the larger negative numbers.)
tofurkey is a vegan turkey substitute, usually made from tofu. at a certain restaurant, the number of calories in a serving of tofurkey with wild mushroom stuffing and gravy is normally distributed with mean 482 and standard deviation 30. find the 92nd percentile of the number of calories. find the 30th percentile of the number of calories. find the third quartile of the number of calories.
Answers
(a) The 92nd percentile of the number of calories is 524.3.
(b) The 30th percentile of the number of calories is 466.4.
(c) The third quartile of the number of calories is 502.1.
What is the percentile of the distribution?To find percentiles in a normally distributed population, we use the standard normal distribution and the z-score formula:
z = (x - μ) / σ
where;
x is the value we want to find the percentile for, μ is the population mean, σ is the population standard deviation, and z is the corresponding z-score.To find the 92nd percentile of the number of calories:
We want to find the value x such that 92% of the servings have fewer calories than x.
This means that we need to find the z-score such that the area to the left of z is 0.92.
Using a standard normal distribution table or calculator, we can find that the z-score corresponding to an area of 0.92 is approximately 1.41.
Then, we use the z-score formula to solve for x:
1.41 = (x - 482) / 30
x - 482 = 42.3
x = 524.3
To find the 30th percentile of the number of calories:
We want to find the value x such that 30% of the servings have fewer calories than x.
This means that we need to find the z-score such that the area to the left of z is 0.30.
Using a standard normal distribution table or calculator, we can find that the z-score corresponding to an area of 0.30 is approximately -0.52.
Then, we use the z-score formula to solve for x:
-0.52 = (x - 482) / 30
x - 482 = -15.6
x = 466.4
To find the third quartile of the number of calories:
The third quartile, denoted Q3, is the value such that 75% of the servings have fewer calories than Q3.
This means that we need to find the z-score such that the area to the left of z is 0.75.
Using a standard normal distribution table or calculator, we can find that the z-score corresponding to an area of 0.75 is approximately 0.67.
Then, we use the z-score formula to solve for x:
0.67 = (x - 482) / 30
x - 482 = 20.1
x = 502.1
Learn more about standard normal distribution here: https://brainly.com/question/26822684
#SPJ1
A businesswoman wants to determine the difference between the costs of owning and leasing an automobile. She can lease a car for $420 per month (on an annual basis). Under this plan, the cost per mile (gas and oil) is $0. 6. If she were to purchase the car, the fixed annual expense would be $4700, and other costs would amount to $0. 08 per mile. What is the least number of miles she would have to drive per year to make leasing no more expensive than purchasing?.
Answers
The least number of miles she would have to drive per year to make leasing no more expensive than purchasing is 48500 miles.
Given:
She can lease a car for $420 per month (on an annual basis). Under this plan, the cost per mile (gas and oil) is $0.06. If she were to purchase the car, the fixed annual expense would be $4700, and other costs would amount to $0. 08 per mile.
Let x be the least miles.
420 * 12 + 0.06x < > 4700 + 0.08x
multiply by 100 on both sides.
504000+6x < > 470000+8x
97000 < > 2x
48500=x
Therefore the least number of miles she would have to drive per year to make leasing no more expensive than purchasing is 48500 miles.
Learn more about the number of miles here:
https://brainly.com/question/620351
#SPJ4
Julia went to the grocery store and purchased cans of soup and frozen dinners. Each
can of soup has 350 mg of sodium and each frozen dinner has 500 mg of sodium.
Julia purchased twice as many cans of soup as frozen dinners and they all collectively
contain 4800 mg of sodium. Write a system of equations that could be used to
determine the number of cans of soup purchased and the number of frozen dinners
purchased. Define the variables that you use to write the system.
Answers
Answer:
2f =c
350c + 500f = 4800
Step-by-step explanation:
Twice as many cans of soup as frozen dinners
All food combined contain 4800 (mg of sodium)
2f =c
350c + 500f = 4800
These are the systems of equations.
Hello can you help me solve this question please

Answers
Answer: Radius=19.2 diameter=38.39
Step-by-step explanation: :DDD
the null hypothesis for the single factor anova states that all means are equal.
T/F
Answers
The null hypothesis for the single factor ANOVA states that all means are equally true.
The null hypothesis for a single-factor ANOVA (analysis of variance) states that all means are equal.
The alternative hypothesis, on the other hand, suggests that at least one of the means is different from the others.
The purpose of the ANOVA test is to determine whether there is sufficient evidence to reject the null hypothesis and conclude that there are significant differences between the means. A statistical formula used to compare variances across the means (or average) of different groups.
Hence, the statement is true .
To know more about null hypothesis click here :
https://brainly.com/question/30821298
#SPJ4
f(n) =5n + 8 when writing a mini prove what first step in evaluating f(-2)
Answers
Please mark it as brainliest

What is half of a 3/4 cup?
Answers
Answer:0.375
Step-by-step explanation:
3/4=0.75
0.75/2=0.375
(3/4)/2=0.375
Can someone help me with this problem?

Answers
Explanation:
The 2 polygons are similar
So 25/30 = 25.5/30.6 = 5/6 or 5:6
what is 6.42 x 10^23 in standard notation
Answers
Answer:
642000000000000000000000
Step-by-step explanation:
Assume propositions p, q, and r have the following truth values: p is true q is false r is true Which compound proposition is true?
Answers
The compound proposition that is true is "p OR q".
To determine which compound proposition is true, we need to analyze the truth values of the individual propositions and apply logical operators to form compound propositions. Let's examine each compound proposition based on the given truth values of p, q, and r: p is true, q is false, and r is true.
1. Proposition 1: (p ∧ q) ∨ r
We have:
p is true (T)
q is false (F)
r is true (T)
Now let's evaluate the compound proposition:
(p ∧ q) ∨ r
Step 1: Evaluate (p ∧ q)
(p ∧ q) is false because q is false. (T ∧ F) is F.
Step 2: Evaluate (p ∧ q) ∨ r
Since (p ∧ q) is false (F) and r is true (T), (p ∧ q) ∨ r is true (T).
Therefore, Proposition 1, (p ∧ q) ∨ r, is true.
2. Proposition 2: ¬p ∧ (q ∨ r)
We have:
p is true (T)
q is false (F)
r is true (T)
Now let's evaluate the compound proposition:
¬p ∧ (q ∨ r)
Step 1: Evaluate ¬p
¬p is false because p is true. ¬T is F.
Step 2: Evaluate (q ∨ r)
(q ∨ r) is true because r is true. F ∨ T is T.
Step 3: Evaluate ¬p ∧ (q ∨ r)
Since ¬p is false (F) and (q ∨ r) is true (T), ¬p ∧ (q ∨ r) is false (F).
Therefore, Proposition 2, ¬p ∧ (q ∨ r), is false.
3. Proposition 3: (p ∨ q) ∧ r
We have:
p is true (T)
q is false (F)
r is true (T)
Now let's evaluate the compound proposition:
(p ∨ q) ∧ r
Step 1: Evaluate (p ∨ q)
(p ∨ q) is true because p is true. T ∨ F is T.
Step 2: Evaluate (p ∨ q) ∧ r
Since (p ∨ q) is true (T) and r is true (T), (p ∨ q) ∧ r is true (T).
Therefore, Proposition 3, (p ∨ q) ∧ r, is true.
Based on the given truth values of p, q, and r, Proposition 1 and Proposition 3 are true, while Proposition 2 is false.
It's important to note that the truth values of the individual propositions and the logical operators used to form the compound propositions determine their overall truth value. In this case, Proposition 1 and Proposition 3 have at least one true component, which makes them true. Proposition 2, on the other hand, has a false component, resulting in a false truth value.
Analyzing the truth values and evaluating compound propositions is a fundamental aspect of propositional logic. It allows us to reason about the relationships between propositions and determine the overall truth or falsity of complex statements based on the truth values of their components.
In this example, by carefully evaluating the truth values of p, q, and r and applying logical operators, we have determined the truth values of the compound propositions. This exercise demonstrates the importance of understanding the principles of propositional logic and how truth values interact when forming compound propositions.
Learn more about compound propositions:
https://brainly.com/question/30545470
#SPJ11
I need help I keep getting it wrong
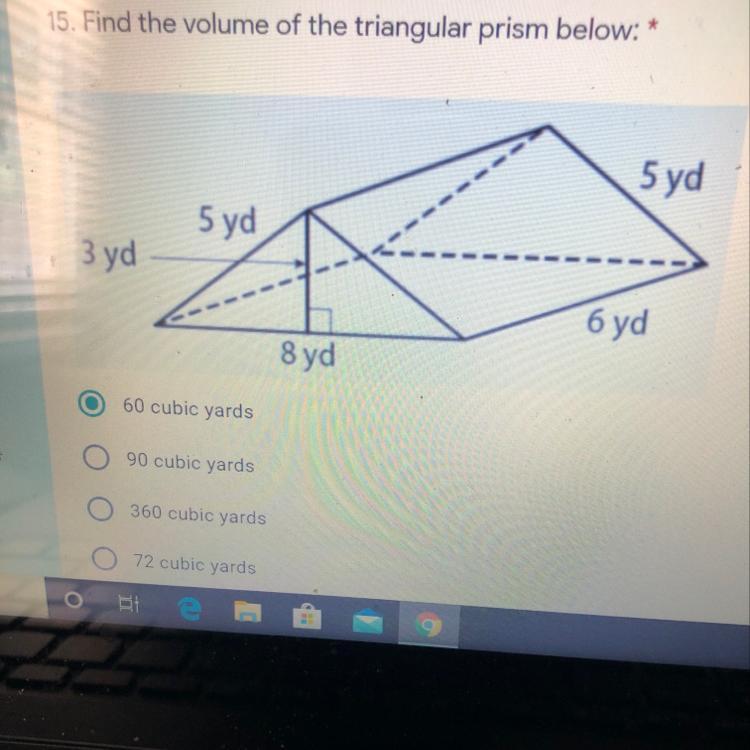
Answers
Find the area of the triangle and multiply by the length of the prism.
Area = 1/2 x 8x3 = 12 square yds.
Volume = 12 x 6 = 72 cubic yards.
A Premier League footballer is value £30 million and after a bad season his transfer value depreciates by 20%. His next season is a good one and his transfer value appreciates by 20%. how Find the value of the footballer after his good season.
How to work out Sir
Answers
Answer:
£28.8 Milllion
Step-by-step explanation:
£30,000,000 × 0.8 = £24,000,000 (Depreciates by 20%)
£24,000,000 × 1.2 = £28,800,000 (Appreciates by 20%)
a matrix consisting entirely of zeros is called a
Answers
A matrix consisting entirely of zeros is called a zero matrix, or an all-zero matrix.
It is denoted with the symbol O and can be written in a matrix form, such as O = [0 0 0 0] where the number of columns and rows depends on the size of the matrix. A zero matrix is a matrix which has all its elements equal to zero. It has a number of special properties that make it useful in linear algebra. For instance, the sum of any two zero matrices is a zero matrix, and any scalar multiple of a zero matrix is a zero matrix. Additionally, the product of two zero matrices is a zero matrix, and the product of a zero matrix and an identity matrix is a zero matrix. These properties make it useful in solving systems of linear equations where all the coefficients are zero. Finally, the inverse of a zero matrix does not exist since its determinant is zero.
Learn more about zero matrix here:
https://brainly.com/question/4470545
#SPJ4
biocalculus [calculus, probability, statistics for the life sciences] by james stewart and troy day webassign
Answers
"Biocalculus: Calculus, Probability, and Statistics for the Life Sciences" by James Stewart and Troy Day is a comprehensive textbook designed to introduce the concepts of calculus, probability, and statistics within the context of life sciences.
"Biocalculus" is specifically tailored for students pursuing life science disciplines, such as biology, biochemistry, and genetics. The book covers essential mathematical topics including limits, derivatives, integration, and differential equations, emphasizing their relevance to biological phenomena and processes. The authors incorporate numerous examples and exercises that focus on real-world applications in areas such as population dynamics, genetics, epidemiology, and pharmacokinetics.
By integrating calculus with probability and statistics, the book equips students with the necessary tools to analyze and interpret data in the life sciences. It introduces key concepts such as probability distributions, hypothesis testing, regression analysis, and experimental design, highlighting their importance in biological research. The authors take a step-by-step approach, providing clear explanations and detailed calculations, ensuring that students grasp the mathematical concepts and their practical implications.
Overall, "Biocalculus: Calculus, Probability, and Statistics for the Life Sciences" serves as an invaluable resource for life science students, helping them develop a strong mathematical foundation and enabling them to apply quantitative methods effectively in their future research and careers.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
What are the missing parts that correctly complete the proof?
Given: Point P is on the perpendicular bisector of segment A B. Prove: Point P is equidistant from the endpoints of segment A B. Art: A horizontal line segment A B with X as the midpoint is drawn. A vertical line X P is drawn. P is above the horizontal line. The angle P X B is labeled as a right angle. The line segments A X and B X are labeled with a single tick mark. A dotted line is used to connect point P with point A. Another dotted line is used to connect point P with point B.
Drag the answers into the boxes to correctly complete the proof.
Statement Reason
1. Point P is on the perpendicular bisector of AB¯¯¯¯¯. Given
2. Response area Definition of bisector
3. ∠PXA and ∠PXB are right angles. Response area
4. Response area All right angles are congruent.
5. PX¯¯¯¯¯≅PX¯¯¯¯¯ Reflexive Property of Congruence
6. Response area SAS Congruence Postulate
7. Response area Corresponding parts of congruent triangles are congruent.
8. Point P is equidistant from the endpoints of AB¯¯¯¯¯. Definition of equidistant
What are the missing parts that correctly complete the proof?
Given: Point P is on the perpendicular bisector of segment A B. Prove: Point P is equidistant from the endpoints of segment A B. Art: A horizontal line segment A B with X as the midpoint is drawn. A vertical line X P is drawn. P is above the horizontal line. The angle P X B is labeled as a right angle. The line segments A X and B X are labeled with a single tick mark. A dotted line is used to connect point P with point A. Another dotted line is used to connect point P with point B.
Drag the answers into the boxes to correctly complete the proof.
Statement Reason
1. Point P is on the perpendicular bisector of AB¯¯¯¯¯. Given
2. Response area Definition of bisector
3. ∠PXA and ∠PXB are right angles. Response area
4. Response area All right angles are congruent.
5. PX¯¯¯¯¯≅PX¯¯¯¯¯ Reflexive Property of Congruence
6. Response area SAS Congruence Postulate
7. Response area Corresponding parts of congruent triangles are congruent.
8. Point P is equidistant from the endpoints of AB¯¯¯¯¯. Definition of equidistant
Answers
Answer:
1. point p is on the perpendicular bisector of AB¯¯¯¯¯- given
2. AXP≅BXP. definition of bisector
3. ∠PXA and ∠PXB are right angles. definition of perpendicular
4. ∠PXA≅ ∠PXB. All right angles are congruent.
5.PX¯¯¯¯¯≅PX¯¯¯¯¯ Reflexive Property of Congruence
6.AXP≅AXQ. SAS Congruence Postulate
7.AX¯¯¯¯¯≅BX¯¯¯¯¯
8.Point P is equidistant from the endpoints of AB¯¯¯¯¯. Definition of equidistant
Step-by-step explanation:
Answer:
1. Point P is on the perpendicular bisector of AB¯¯¯¯¯. Given
2. AX¯¯¯¯¯≅BX¯¯¯¯¯¯ . Definition of bisector
3. ∠PXA and ∠PXB are right angles . Definition of Perpendicular
4. ∠PXA and ∠PXB . All right angles are congruent.
5. PX¯¯¯¯¯≅PX¯¯¯¯¯ . Reflexive Property of Congruence
6. △AXP≅△BXP . SAS Congruence Postulate
7. PA¯¯¯¯¯≅PB¯¯¯¯¯ . Corresponding parts of congruent triangles are congruent
8. Point P is equidistant from the endpoints of AB¯¯¯¯¯ . Definition of equidistant
Step-by-step explanation:
Find the area of the circle.
18 ft
A
1017.9 ft2
B
254.5 ft?
С
113.1 ft2
D
339.3 ft2

Answers
Answer:
A.
Step-by-step explanation:
The formula for trying to find the area of a circle is Area= r^2
Sooo:
Area=3.14 x 18 x 18
18 x 18 is the first part of the equation
=324
Then:
3.14(pi) x 324 = 1017.36 = 1017 ft2
the following data represent the weight of a child riding a bike and the rolling distance achieved after going down a hill without pedaling. weight (lbs.) rolling distance (m.) 59 26 83 43 97 49 56 20 103 65 87 44 88 48 91 42 52 39 63 33 71 39 100 49 89 55 103 53 99 42 74 33 75 30 89 30 102 40 103 33 99 33 102 35 86 37 85 37 can it be concluded at a 0.01 level of significance that there is a linear correlation between the two variables?
Answers
Yes, it can be concluded at a 0.01 level of significance that there is a linear correlation between the two variables.
The following is a solution to the given question. The weight of a child riding a bike and the rolling distance achieved after going down a hill without pedaling is given by the data. The correlation coefficient between the two variables is to be tested to conclude if there is a linear correlation between the two variables at a 0.01 level of significance.
Linear correlation between the two variables A correlation coefficient, r, is used to determine if two variables have a linear correlation. A value of r=1 indicates a perfect positive correlation, while a value of r=-1 indicates a perfect negative correlation. A value of r=0 indicates no correlation between the two variables.To find the correlation coefficient, we use the following formula:
\($r = \frac{n\sum xy - \sum x\sum y}{\sqrt{(n\sum x^2 - (\sum x)^2)(n\sum y^2 - (\sum y)^2)}}$\)
Where
n is the number of data points x and y are the two variables.Weight, \($x$\) Rolling Distance \($y$59 2683 4397 4956 20103 6587 4488 4891 4252 3963 3371 39100 4989 55103 5399 4274 3375 3089 30102 40103 3399 3386 3785 37\)
We need to find n,
\($\sum x$\) \($\sum y$\) \($\sum x^2$\)\($\sum y^2$\)
\(\sum xy$.n=30$\\ \sum x=2792$$\\ \sum y=1129$$\\ \sum x^2=221506$$\\ \sum y^2=86223$$\\ \sum xy=106883$r = 0.91\)
Correct to two decimal places.
Decision RuleWe have to check if the value of r lies in the critical region for a 0.01 level of significance. The value of r that separates the critical region from the non-critical region is found using the following formula:
\($$r_c = \frac{1}{\sqrt{n-2}}$$\)
Where n is the sample size.
Substituting the values, we get
\($$r_c = \frac{1}{\sqrt{30-2}} = 0.366$$\)
The critical region is when r is greater than 0.366 or less than -0.366.
Conclusion The value of r (0.91) is greater than the critical value (0.366). Hence, we conclude that there is a linear correlation between the two variables at a 0.01 level of significance. Therefore, the answer is: Yes, it can be concluded at a 0.01 level of significance that there is a linear correlation between the two variables.
See more about linear correlation at: https://brainly.com/question/13828699
#SPJ11
can someone help me on this please

Answers
Answer:
The answer is Option A
Step-by-step explanation:
Start by dividing 54 by 6 which will give you 9
then divide b² by b^5 which will give you b³ at the denominator
then a^8÷a^-4
using indices...
=a^8-(-4)
=a^12
at the numerator
put everything together and you'll have...
9a^12/b³
A. \( \frac{9 \: {a}^{12} }{ {b}^{3} }\) ✅
\(\large\mathfrak{{\pmb{\underline{\red{Step-by-step\:explanation}}{\orange{:}}}}}\)
\(54 {a}^{8} {b}^{2} \div 6 {a}^{ - 4} {b}^{5} \)
To solve the expression in a simpler way, single out the like terms.
Now, we have
\( \frac{54}{6} . \frac{ {a}^{8} }{ {a}^{ - 4} } . \frac{ {b}^{2} }{ {b}^{5} } \\ \\ = 9 \: {a}^{8 - ( - 4)} {b}^{2 - 5} \\ \\ (∵ \frac{ {a}^{m} }{ {a}^{n} } = {a}^{m - n} ) \\ \\ = 9 \: {a}^{8 + 4} {b}^{ - 3} \\ \\ = 9 \: {a}^{12} {b}^{ - 3} \\ \\ ( \: or \: ) \\ \\ = \frac{9 \: {a}^{12} }{ {b}^{3} } \\ \\ (∵ {a}^{ - m} = \frac{1}{ {a}^{m} } )\)
\(\large\mathfrak{{\pmb{\underline{\orange{Happy\:learning }}{\orange{!}}}}}\)
Solution: The set of all elements in the universal set that is not in set A is called the complement of set A.
Answers
The complement of set A, denoted by ​ A`, is the collection of all elements that belong to the universal set but are not part of set A. It's not necessary to mention the universe (also known as U) if it's understood which set of elements is being referred to.
The complement of a set A is the collection of all elements that belong to the universal set but not to set A. It is denoted as ​ A` and does not include any elements that are already in set A. The universal set, also known as U, contains all possible elements and is assumed to be known. Therefore, when referring to the complement of a set, it is not necessary to mention the universal set explicitly. The complement of a set is useful in determining the set of elements that are not part of a particular set, and it can be used in various mathematical operations.
Learn more about mathematics here: brainly.com/question/24600056
#SPJ4
A small class has 9 students, 6 of whom are girls and 3 of whom are boys. The teacher is going to choose two of the students at random. What is the probability that the teacher will choose two boys? Write your answer as a fraction in simplest form.
Answers
The probability of selecting the first boy is 3/9 (since there are 3 boys out of 9 students). After selecting the first boy, there will be 2 boys left out of the remaining 8 students.
Therefore, the probability of selecting the second boy, given that the first boy was chosen, is 2/8.
To find the probability of both events occurring (selecting two boys in a row), we multiply the probabilities:
(3/9) * (2/8) = 6/72 = 1/12
So, the probability that the teacher will choose two boys is 1/12.
A football is punted from a height of 3.5 feet about the ground with an initial velocity of 45 feet per second. This situation can be represented by the function h(t)=- 16t^2 + 45t + 3.5, where t is the number of seconds elapsed since the football was kicked. If the football is caught at a height of 5.5ft on the ball's descent, how long was the football in the air? Round to the nearest hundredth.
*show me how you did it not just the answer please
Answers
The time at which the ball was in the air for the two cases of being dropped and being caught are respectively; t = 0.05 s and t = 2.77 s
What was the time of descent?We are given the function to represent the given height as;
h(t)= -16t² + 45t + 3.5
Since the football is caught at a height of 5.5ft on the ball's descent, then;
-16t² + 45t + 3.5 = 5.5
⇒ -16t² + 45t - 2 = 0
From online quadratic equation solver, we have;
t = 0.05 s and t = 2.77 s
Read more about projectile motion at; https://brainly.com/question/11049671
