How many pairs of parallel lines are in the image below
Answers
A pair of parallel lines are the ones that never meet on the plane, they can never intersect regardless of how much we extend both lines.
So, using the definition above, we can notice that there is a line that intersects the other three lines. Therefore, that one cannot be parallel with any of the others three lines.
As for the remaining three lines, we see that each of those is parallel to any of the others, so, the three lines are parallel. However, we need to identify pairs of parallel lines, since we have 3 parallel lines, there are 3 different pairs that we can form with them (1,2), (2,3), (3,1).
Therefore, there are 3 pairs of parallel lines in the image.
Related Questions
Find the exact value of the expression. cos(160°) cos(10°) + sin(160°) sin(10°)
Answers
Answer:
Step-by-step explanation:
cos a cos b+sin a sin b=cos (a-b)
cos 160 cos 10+sin 160 sin 10=cos (160-10)
=cos 150
=cos (180-30)
=-cos 30
=-√3/2
The value of the given trigonometric expression is -0.8659.
What are trigonometric angles?Trigonometric angles are the angles in a right-angled triangle using which different trigonometric functions can be represented. Some standard angles used in trigonometry are 0º, 30º, 45º, 60º, 90º.
The given expression is cos(160°) cos(10°) + sin(160°) sin(10°).
Here, cos160° = -0.9396
cos10° = 0.9848
sin160° = 0.3420
sin10° = 0.1736
(-0.9396)×0.9848+0.3420×0.1736
= -0.8659
Therefore, the value of the given trigonometric expression is -0.8659.
Learn more about the trigonometric angles visit:
brainly.com/question/24174128.
#SPJ2
Rework problem 17 from section 2.1 of your text, involving an experiment with three possible outcomes. For this problem, assume that outcome O1 has frequency 4/a, outcome O2 has frequency 12/a, and outcome O3 has frequency 3/a.
What is the value of a?
Answers
If outcome O₁ has a frequency 4/a, outcome O₂ has a frequency 12/a, and outcome O₃ has frequency 3/a, then the value of a is 19
Frequency of outcome O₁ = 4/a
Frequency of outcome O₂ = 12/a
Frequency of outcome O₃ = 3/a
Let's say 1/a = x
Now, the Frequency of outcome O₁ = 4x
Frequency of outcome O₂ = 12x
Frequency of outcome O₃ = 3x
The sum of the respective frequencies must equal 1.
So, 4x + 12x + 3x = 1
19x = 1
x = 1/19
That means that the “a” in the problem is 19.
To learn more about frequency here:
brainly.com/question/14169579
#SPJ4
Rajan baut a book for Rs 180 and sold it to sajan at a profit of 20%. Sajan sold that book to nirajan at a lost 20%. At what price nirajan should sell the book to receive 5% profit ?
Answers
Solution,
CP for rajan=180 rs
Sp for rajan=(20%+1)×180
=216
Cp for niranjan=216
And, Sp=.8×216
=172.8
Cp for niranjan=172.8
For 5% profit,
Sp for Niranjan=(5%+1)×172.8
=181.44
Hence, for Niranjan to gain 5% profit, he must sell it for 181.44 rs
Answer - 181.44
Explanation - For Rajan,
Cost Price = Rs 180
Profit Percent = 20%
Profit Percent = (S.P - C.P/C.P)*100
20 = (S.P - 180/180) *100
S.P = Rs 216
For Sajan,
C.P = Rs 216
Loss Percent= 20%
Loss = (C.P - S.P/C.P)*100
20 = (216-S.P/216)*100
S.P = Rs 172.8
For Niranjan to Sell Book and get 5% profit,
C.P = Rs 172.8
Profit Percent = (S.P - C.P/C.P)*100
5 = (S.P-172.8/172.8)*100
S.P = 181.44
URGENT!!!!! WILL MARK BRAINLIEST!!!!
Options:
AAS
SAS
AAA
ASA

Answers
The large solid below is made from small cubes. Each has a side length of 1/5. Answer the questions below. Write your answers in simplest form. (c) What is the volume of the large solid?
Answers
The volume of the large solid is equal to 8/25 cm³.
How to calculate the volume of a cube?In Mathematics, the volume of a cube can be calculated by using the following formula:
V = m³
Where:
V represents the volume of a cube.m is the side lengths of a cube.By substituting the given points into the formula for the volume of a cube, we have the following;
Volume of cube, V = m³
Volume of cube, V = (1/5)³
Volume of cube, V = 1/125 cm³.
For the volume of the large solid, we have:
Volume of large solid = 5 × 2 × 4 × 1/125
Volume of large solid = 8/25 cm³.
Read more on volume of a cube here: brainly.com/question/25248189
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

I NEED HELP PLEASE, THANKS! :)

Answers
Answer:
\(\frac{6^2-3^2}{2} =\frac{27}{2}\)
(the third answer in your list of options)
Step-by-step explanation:
The area of the region between y = x, and the x axis, between x= 3 and x=6 is the area of the trapezoid shown in the attached image.
It therefore can be calculated via the area of a trapezoid:
\((B+b)\,H/2=(6+3)*3/2=27/2\)
or doing the integral (which it seems is what they want you to do):
\(\int\limits^6_3 {x} \, dx =\frac{x^2}{2} ]\limits^6_3=\frac{6^2-3^2}{2} =\frac{27}{2}\)

Write this number in standard form 3 thousands, 16 tens,7 ones
Answers
Please can someone explain this question to me step-by step, i have a exam this Wednesday so pleasee help me!! Help is greatly greatly appreciated ^^
Thankyou!!
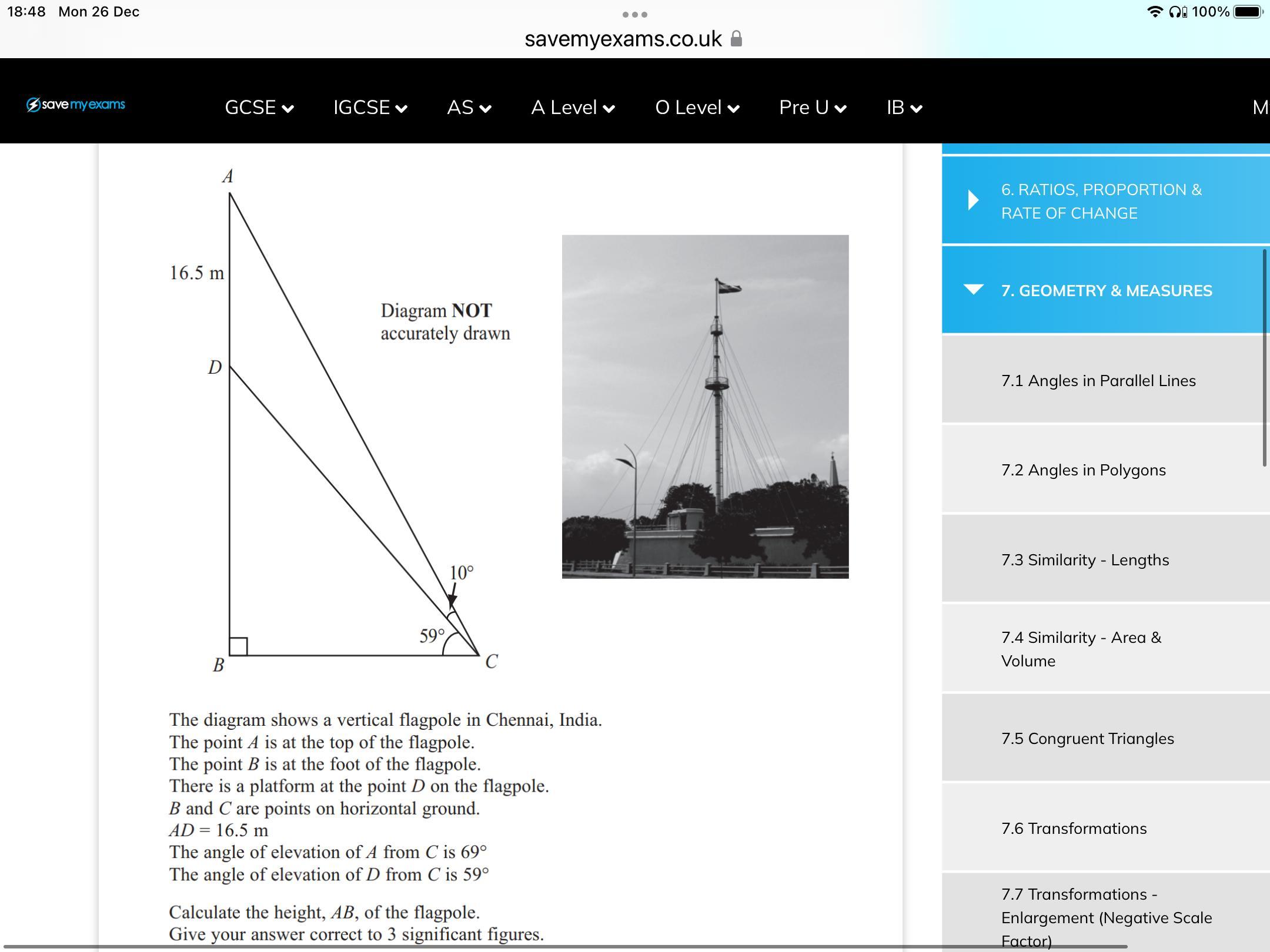
Answers
Answer:
AB = 45.688 metres
Step-by-step explanation:
* i used a scientific calculator for my working. i am not sure if calculators are permitted for your exam on Wednesday *
⭐AB = AD + DB
⭐AB = 16.5 + DB
Thus, we need to find DB in order to solve for AB.
First, I utilized the triangle sum theorem to find ∠BDC:
\(< BDC + < DCB + < B = 180\\ < BDC + 59 + 90 = 180\\ < BDC + 149 = 180\\ < BDC = 31\)
Then, I utilized the linear pair sum to find ∠ADC:
\(< ADC + < BDC = 180\\ < ADC + 31 = 180\\ < ADC = 149\)
Next, I utilized the triangle sum theorem to find ∠DAC:
\(< DAC + < ADC + < ACD = 180\)
\(< DAC + 149 + 10 = 180\)
\(< DAC + 159 = 180\)
\(< DAC = 21\)
After, I utilized the law of sines to find DC:
\(\frac{sin10}{16.5} = \frac{sin21}{DC}\)
\(DCsin10 = 16.5sin21\)
\(DC = \frac{16.5sin21}{sin10}\)
\(DC = 34.052\)
Then, I utilized the sine function to find DB for ΔBDC:
\(sin(59) = \frac{DB}{34.052}\)
\(34.052sin(59) = DB\)
\(29.188 = DB\)
Finally, I substituted DB into our original equation for AB:
\(AB = AD + DB\)
\(AB = 16.5 + 29.188\)
\(AB = 45.688 metres\)
Good luck on your exam on Wednesday! :-)
The height of the pole will be equal to 45 meters.
What are trigonometric identities?
Trigonometric Identities are equality statements that hold true for all values of the variables in the equation and that use trigonometry functions. There are numerous distinctive trigonometric identities that relate to a triangle's side length and angle.
Given that the angle BCD is 59 and the angle BCA is 69. The height will be calculated as,
tan(59) = BD / BC
BC = BD / tan(59)
BC = 0.6BD
tan(69) = AB / BC
tan(69) = ( 16.5 + BD ) / BC
BC = 0.38( 16.5 + BD )
Equate the values of BC,
0.6BD = 0.38 ( 16.5 + BD )
0.6BD = 6.27 + 0.38BD
0.22BD =6.27
BD = 28.5 meters
The height of the pole is,
AB = AD + DB
AB = 16.5 + 28.5
AB = 45 meters
The height is 45 meters.
To know more about trigonometry follow
https://brainly.com/question/25224151
#SPJ2
SELECT ALL of the numbers that are included within the range of the line segment.
ANSWERS ↓
-6
-4
-3
-2
0.5
1.5
3.5

Answers
Answer: -2, -3, and -4.
Step-by-step explanation:
The range is all the Y Values the graph uses, and the Y values range from -0.5 to -5.5, making every number in between those included.
The airport security randomly selected 36 suitcases from the security line. Of these bags, they screened 8 suitcases. What is the most reasonable prediction for the number of suitcases they will screen in a group of 180?
Answers
find the value of 3√x +7 if x = 25

Answers
Given the expression
\(\begin{gathered} 3\sqrt[]{x}+7 \\ \end{gathered}\)Given that x = 25
Substitute 25 for x into the expression above
\(\begin{gathered} \text{Where x = 25} \\ 3\sqrt[]{x}+7=3\sqrt[]{25}+7 \\ =3\sqrt[]{25}+7=3(5)+7 \\ =3(5)+7=15+7 \\ =15+7=22 \end{gathered}\)Hence, the answer is 22
Question
2. Determine
the
acute
angle
between the planes
x - 2y + 5z = 3
2x + y - 3z = 15.
Distance of a plane from the origin:
Answers
Answer:
Acute angle between the two planes: approximately \(43^\circ\).
Step-by-step explanation:
Find the normal vector of each plane:
The normal vector of the plane \(x - 2\, y + 5\, z = 3\) is \(\displaystyle \begin{bmatrix}1 \\ -2 \\ 5\end{bmatrix}\).The normal vector of the plane \(2\, x + y - 3\, z = 15\) is \(\displaystyle \begin{bmatrix}2 \\ 1\\ -3\end{bmatrix}\).As the name suggests, there is a \(90^\circ\) angle between a plane and its normal vector. The following four angles will correspond to the vertices of a quadrilateral:
The \(90^\circ\) angle between the first plane and its normal vector.The angle between the normal vector of each plane.The \(90^\circ\) angle between the second plane and its normal vector.The smallest angle between these two planes.The sum of these four angles should be \(360^\circ\). Two of these four angles were known to be \(90^\circ\). Once the third angle (the angle between the two normal vectors) is found, subtractions would give the measure of the other angle (the smallest angle between these two planes.)
Make use of the dot product to find the angle between these two normal vectors. Let \(\theta\) denote the angle between these two vectors.
\(\displaystyle \cos \theta = \frac{\begin{bmatrix}1 \\ -2 \\ 5\end{bmatrix} \cdot \begin{bmatrix}2 \\ 1 \\ -3\end{bmatrix}}{\sqrt{1^2 + (-2)^2 + 5^2} \cdot \sqrt{2^2 + 1^2 + (-3)^2}} \approx -0.73193\).
Before continuing, notice that the smallest angle between the two planes would be \(360^\circ - 90^\circ - 90^\circ - \theta = 180^\circ - \theta\).
Consider the identity: \(\cos\left(180^\circ - \theta\right) = -\cos \theta\).
In other words, \(\cos\left(180^\circ - \theta\right)\), the cosine of the smallest angle between the two planes (which the question is asking for) will be the opposite of \(\cos \theta\), the cosine of the angle between the two normal vectors.
Therefore, the cosine of the smallest angle between the two planes will be \(-(-0.73193) = 0.73193\).
Apply the inverse cosine function to find the size of that angle:
\(\arccos(0.73193) \approx 43^\circ\).
A school spent $780,000 in one year to pay all of its teachers and administrators. The school has a total of twenty-four teachers and administrators combined. If teachers make $35,000 per year and administrators make $40,000 per year, how many teachers and how many administrators does the school have?
Answers
Answer: Impossible
Step-by-step explanation: Even if 24 people were on the teacher salary, 780,000 still couldn't cover them all.
Add, answer as a fraction:
1/15 + 3/12
A) 10/67
B) 12/27
C) 19/60
D) 4/27
Answers
Answer:
Hello, There! I'll be glad to help!
Question1/15 + 3/12
Answer\(\boxed{Option ~C. ~19/60}\)
Step-by-step explanation:
\(\frac{1}{15} +\frac{3}{12} =\frac{1 ~x~4}{15~x~4} +\frac{3~x~5}{12~x~5} =\)
\(\frac{4}{60} +\frac{15}{60} = \frac{19}{60}\)
Therefore, Your Answer is (Option C.)
Enter a number in each blank M(x)=(2x-6)(x-4) true statements when M(x)=0 when x=
Answers
Answer:
{3, 4}
Step-by-step explanation:
"M(x)=(2x-6)(x-4) true statements when M(x)=0 when x= ?" asks us to find the "roots" of M(x); that is, the x values at which M(x) = 0. Thus, we set
(2x - 6)(x - 4) = 0, which is equivalent to 2(x - 3)(x - 4) = 0.
Thus, x - 3 = and x = 3; also x - 4 = 0, so that x = 4.
The roots of M(x) are {3, 4}
Using the language of the original problem: "true statements when M(x)=0 when x=" the correct results, inserted into the blanks, are x = 3 and x = 4.
Help its urgent i need to get these done

Answers
The planes that are parallel in the cube shown would be C. NOR and LMP.
What are parallel planes ?Two planes that are located on a cube and are always opposite and never intersect; they remain continuously at the same distance from each other. A cube consists of three pairs of parallel planes in correspondence with its triplet of opposing faces.
From the given options, the only parallel planes would be NOR and LMP. One of the reasons for this, is that these planes have no point of intersection unlike the planes in the other options.
Find out more on parallel planes at https://brainly.com/question/29329147
#SPJ1
Question 7
Jorge earned 91, 84, 87 on his first three out of four Algebra tests. He wants to get an
average of 90 in the class. What should he make on his last test to achieve this goal?
Answers
To earn an average score of 90, the score on the fourth test needs to be 98.
What is average?The core value of a set of data is expressed mathematically as the average of a list of data. It is defined mathematically as the ratio between the total number of units in the list and the sum of all the data. The term "mean" in statistics also refers to the average of a particular set of numerical data.
Given the score of the first three tests as:
91, 84, 87.
The average is given by the following formula:
Average = Sum of scores ÷ total number of tests
Let us suppose the score of fourth test as x.
Given that A = 90:
90 = (91 + 84 + 87 + x) ÷ 4
x = 98
Hence, the score on the fourth test must be equal to 98, to get an average score of 90.
Learn more about average here:
https://brainly.com/question/24057012
#SPJ1
How can I solve this? Thank you in advance!!
One number is randomly selected from {1, 2, 3, 4, 5, 6, 7, 8, 9}. Find the probability that the selected number is an odd number or a multiple of 3.
Answers
Answer:
The probability that the selected number is an odd number or a multiple of 3 is 6/9, or 2/3. This is because there are 6 numbers that meet the criteria out of the 9 numbers in the set: 1, 3, 5, 7, 9, and 3.
i really need help on this problem! reply asap!!!

Answers
A big = 112.5
A shaded = 112.5 - 32.5 = 80
718.012 in expanded form and written form
Answers
Answer:
Expanded Form BelowWritten Form BelowStep-by-step explanation:
Expanded Form = 700 + 10 + 8 + 0.01 + 0.002
Written Form = Seven-Hundred Eighteen, Point Twelve-Hundredths
Hope this helps! <3
Use the power-reducing formulas to rewrite the expression in terms of first powers of the cosines of multiple angles.
sin^8(x)

Answers
The answer for the given expression is =1/128[35-56cos2x+28cos4x-8cos6x+cos8x]
What is trignomatric functions?
All trigonometric identities are built upon the foundation of the six trigonometric ratios. Some of their names are sine, cosine, tangent, cosecant, secant, and cotangent. The adjacent side, opposite side, and hypotenuse side of the right triangle are used to define each of these trigonometric ratios.
What is multiple angles?
If angle A is taken as a given, then many angles are 2A, 3A, 4A, etc. The many angle formulas employ the double and triple angles formulas. Sine, cosine, and tangent are the often utilised trigonometric functions for the multiple angle formula.
Answer is attached as a image must check:
To know more about tangent visit:
https://brainly.com/question/14022348
#SPJ1

We can rewrite sin⁸x in terms of first powers of the cosines of multiple angles as:
sin⁸x = 1/128 (35 - 4cos²x + 40cos⁴x - 64cos⁶x + cos⁸x)
What is power reducing formula?Trigonometric functions raised to powers can be rewritten using double-angle, half-angle, and Pythagorean identities in power lowering formulas. Equations can be made simpler using them, and trigonometric expressions can be precisely determined.
We can use the power-reducing formulas to rewrite sin⁸x in terms of cosines of multiple angles as follows:
sin²x = 1 - cos²x (first power-reducing formula)
sin⁴x = (sin²x)² = (1 - cos²x)²
= 1 - 2cos²x + cos⁴x (second power-reducing formula)
sin⁶x = (sin⁴x)(sin²x)
= (1 - 2cos²x + cos⁴x)(1 - cos²x)
= 1 - 3cos²x + 3cos⁴x - cos⁶x (third power-reducing formula)
sin⁸x = (sin⁶x)(sin²x)
= (1 - 3cos²x + 3cos⁴x - cos⁶x)(1 - cos²x)
= 1 - 4cos²x + 6cos⁴x - 4cos⁶x + cos⁸x
Now we can substitute the expression for sin⁸x into the given expression and simplify it:
1/128 (35 - 56 cos2x + 28 cos4x - 8 cos6x + cos8x)
= 1/128 (35 - 56(2cos²x-1) + 28(4cos⁴x-3cos²x) - 8(8cos⁶x-8cos⁴x+cos²x) + cos⁸x)
= 1/128 (35 - 112cos²x + 56 + 112cos⁴x - 84cos²x - 64cos⁶x + 64cos⁴x - 8cos²x + cos⁸x)
= 1/128 (35 - 4cos²x + 40cos⁴x - 64cos⁶x + cos⁸x)
Therefore, we can rewrite sin⁸x in terms of first powers of the cosines of multiple angles as:
sin⁸x = 1 - 4cos²x + 6cos⁴x - 4cos⁶x + cos⁸x
= 1/128 (35 - 4cos²x + 40cos⁴x - 64cos⁶x + cos⁸x)
Learn more about power reducing formulas on:
https://brainly.com/question/29586028
#SPJ1
PLEASE HELP ME RIGHT NOW ASAP

Answers
Answer:
Step-by-step explanation:
Let's just say this circle has value x.
x increases by 5%, or 0.05 of x.
x + 0.05x = 1.05x
1.05x now increases by 5% again:
1.05x + 0.05(1.05x) = 1.1025x
The total increase is equal to (1.1025-1)*100 = 10.25%
Hope this helps!
Geometry question, question in photo attachment

Answers
Answer:
323/7 or about 46.143
Step-by-step explanation:
We can infer that the measure of B + C is 90 degrees, so 6x + 1 + 8x - 11 must be equal to 90.
6x + 1 + 8x - 11 = 90
14x - 10 = 90
14x = 100
x = 100/14
x = 50/7
Solve for the measure of C by substituting x with 50/7.
50/7 * 8 = 400/7
400/7 - 11 = 323/7
the measure of C is 323/7
Help! Quick! Find the area of the composite figure

Answers
Answer:
60m
Step-by-step explanation:
To find the area of the triangle you multiply the base by height and divide by two, but we don’t know the base of the triangle!
Luckily, the bottom of the triangle is a rectangle. Rectangles are symmetrical, and the other side of the rectangle is 8.
So, the base of the triangle is 8.
Now let’s find the area of the triangle:
8 x 5 = 40
40/2 = 20
20 is the area of the triangle
Now, we must find the area of the rectangle!
The formula for rectangle area is just width x length:
8 x 5 = 40
Add them together:
40 + 20 = 60
Therefore, the area is 60m.
Is 0.3682 a non-repeating decimal?
Answers
Answer:
its a non-repeating decimal
Step-by-step explanation:
repeating decimals continue you on for a while, if decimals have a line over top of the last ending number that means it kept repeating so they cut it short, this one however doesn't have that symbol.
A particular disease is tested for and the results determine that it occurs in about 1 of every 750 Hispanic females and about 1 of every 138,000 non-Hispanic females 26,000 Hispanic females were to be tested, about how many of them would you expect to have this particular disease?
Answers
Approximately 34.658 Hispanic females out of 26,000 to have this particular disease.
Hispanic female;A woman or girl who identifies as Hispanic or Latino, which usually refers to persons of Spanish-speaking origin or lineage from Latin America or Spain, is referred to as a "Hispanic female."
The proportion of Hispanic females with the disease is 1 in 750, which can be expressed as:
1 / 750 = 0.001333
This means that for every 750 Hispanic females, one is expected to have the disease.
To calculate the expected number of Hispanic females with the disease in a group of 26,000, we can multiply the proportion by the total number of Hispanic females:
0.001333 * 26,000 = 34.658
So we would expect approximately 34.658 Hispanic females out of 26,000 to have this particular disease.
To know more about proportion:
https://brainly.com/question/24232216
#SPJ1
Compare the investment below to an investment of the same principal at the same rate compounded annually.
principal: $5,000, annual interest: 9%, interest periods: 4, number of years: 18
After 18 years, the investment compounded periodically will be worth $? more than the investment compounded annually.
(Round to two decimal places as needed.)
Answers
After 18 years, the investment compounded periodically (quarterly) will be worth $1,230.23 more than the investment compounded annually.
What is compounded interest?Compounded interest refers to the interest system that charges interest on both principal and accumulated interest.
The period of compounding in a year determines the worth of the future value.
The future value can be ascertained using an online finance calculator as follows:
Interest periods: = 4 times yearly (Quarterly)
Principal = $5,000
Annual interest rate = 9%
Number of years: 18
N (# of periods) = 72 quarters (18 years x 4)
I/Y (Interest per year) = 9%
PV (Present Value) = $5,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $24,815.83
Total Interest = $19,815.83
Interest periods: = Annually
N (# of periods) = 18 years
I/Y (Interest per year) = 9%
PV (Present Value) = $5,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $23,585.60
Total Interest = $18,585.60
Difference in Future Values $1,230.23 ($24,815.83 - $23,585.60)
Thus, an investment compounded periodically earns more than an investment compounded annually.
Learn more about compounded interest at https://brainly.com/question/28020457.
#SPJ1
what is between fractions 6/6 and 6/7
Answers
The fraction 13/7 lies between the fractions 6/6 and 6/7.
We have,
Between the fractions 6/6 and 6/7, there are infinitely many fractions.
To find a fraction that lies between these two fractions, we can take their average.
The fraction 6/6 simplifies to 1, and the fraction 6/7 cannot be simplified further.
To find the average, we add the two fractions and divide the sum by 2:
(6/6 + 6/7) / 2
To add the fractions, we need a common denominator, which is the least common multiple (LCM) of 6 and 7, which is 42.
Converting the fractions to have a common denominator:
(6/6) x (7/7) + (6/7) x (6/6) / 2
Simplifying the expression:
(42/42 + 36/42) / 2
Combining the numerators:
(78/42) / 2
Dividing:
78/42 = 13/7
Thus,
The fraction 13/7 lies between the fractions 6/6 and 6/7.
Learn more about fractions here:
https://brainly.com/question/24370499
#SPJ1
Opal saves $7. A week for 16 weeks. Her brother saves $27. A month for 4 months. Who saves more money?
Answers
Answer:
Opal saves more
Step-by-step explanation:
Eastern Ice Company sells 10 pound blocks of ice in the shape shown. The volume of the block of ice is 375 Inches cubed. What is the height of the block of ice?
A block of ice has a length of 10 inches and a width of 7.5 inches.
Use the formula Height = StartFraction Volume Over length times width EndFraction, where l is the length of the prism, w is the width, V is the volume, and h is the height.
2.5 inches
4 inches
5 inches
7.5 inches
Answers
Answer:
2.5
Step-by-step explanation:
A block of ice has a length of 10 inches and a width of 7.5 inches. Therefore, the height of the ice is 5 inches.
How to find the volume of the cuboid?Let the three dimensions(height, length, width) be x, y,z units respectively.
Then the volume of the cuboid is given as
\(V = x \times y \times z \: \rm unit^3\)
Eastern Ice Company sells 10-pound blocks of ice in the shape shown. The volume of the block of ice is 375 inches cubed.
A block of ice has a length of 10 inches and a width of 7.5 inches.
Let z be the height of the ice.
Then the volume of the is given as
\(V = x \times y \times z \: \rm unit^3\)
\(375 = 10 \times 7.5 \times z \: \rm unit^3\\\\z = 5\)
Therefore, the height of the ice is 5 inches.
Learn more about cuboid here:
https://brainly.com/question/13522634
#SPJ2