I don’t know if this is correct !!!!!!! Please answer correctly !!!!!!! Will mark Brianliest !!!!!!!!!

Answers
And it can be proven
Answer:
It is correct how you put it
Related Questions
What is the midpoint between 0 and n?
Answers
Find the distance if the rate is 78.5 mph and the time is 4.5 hours.
Answers
Answer:
353.25 miles.
Step-by-step explanation:
multiply 78.5 mph by 4.5 hours
find a function f such that f '(x) = 3x^3 and the line 81x + y = 0 is tangent to the graph of f.
Answers
A function f such that f '(x) = 3x^3 and the line 81x + y = 0 is tangent to the graph of f is f(x) = 3x^4/4 + 729/4.
In the given question, we have to find a function f such that f'(x) = 3x^3 and the line 81x + y = 0 is tangent to the graph of f.
The given function is f'(x) = 3x^3.
No integrating on both side,
f(x) = \(\int3x^3dx\) + C
f(x) = 3x^4/4 + C
As given, the line 81x + y = 0 is tangent to the graph of f.
So, slope at point of tangent; f'(x) = -81
So, 3x^3 = -81
Divide by 3 on both side, we get
x^3 = -27
Taking cube root on both side, we get
x = -3
So putting the value of x in 81x + y = 0, we get
y = 243
Thus, f(x) passes through (-3, 243).
So, 243 = 3/4(81) + C
Multiply by 4 on both side, we get
972 = 243 + 4C
Subtract 243 on both side, we get
4C = 729
Divide by 4 on both side, we get
C = 729/4
So, f(x) = 3x^4/4 + 729/4
To learn more about function link is here
brainly.com/question/21145944
#SPJ4
3) Kites are manufactured by identical firms. Each firm's total and marginal cost functions for weekly production are given by TC=0.01q2+100MC=0.02q In the long-run equilibrium, how many kites will each firm produce? Describe the long-run supply curve for kites. a. Suppose the weekly demand for kites is given by QD=4000−1000P. How many kites will be sold? How many firms will there be in the kite industry? b. Suppose that the weekly demand for kites suddenly goes up to QD=5000−500P. In the very short run, when it is impossible to manufacture any more kites than those produced for that weck, what will the price of kiter be? How much profit will cach kite maker cam? In the market short run, what will the price of kites be? How much profit will cach kite maker carn'? d. In the market long run, what will the price of kites be? How many new firms will enter the kite-making industry? How much profit will they carr? Be sure to show your work.
Answers
To determine the long-run equilibrium for each firm's production of kites, we need to find the level of output where marginal cost (MC) equals marginal revenue (MR). In perfect competition, firms maximize their profit by producing at the level where MC = MR.
Given the marginal cost function MC = 0.02q, we equate it to the marginal revenue, which is equal to the market price (P) in perfect competition. So, we have:
0.02q = P
Now, we need to find the price at which the quantity demanded (QD) equals the quantity supplied (QS) in the market. To do this, we set QD equal to QS:
QD = QS
Substituting the demand function QD = 4000 - 1000P into the equation, we get:
4000 - 1000P = QS
Now, we can solve for the price (P):
4000 - 1000P = 0.02q
Simplifying further:
1000P = 4000 - 0.02q
P = (4000 - 0.02q) / 1000
Now, we can substitute the value of P into the equation for MC to find the level of output (q):
0.02q = P
0.02q = (4000 - 0.02q) / 1000
Solving for q:
0.02q = 4 - 0.00002q
1.00002q = 4
q = 4 / 1.00002
q ≈ 3999.8
In the long-run equilibrium, each firm will produce approximately 3999.8 kites.
The long-run supply curve for kites in perfect competition is horizontal at the minimum average total cost (ATC) of the firms. This is because in the long run, firms have enough time to adjust their inputs and optimize their production processes, leading to production at the lowest possible cost.
a. To find the number of kites sold and the number of firms in the kite industry, we substitute the price (P) into the demand function QD = 4000 - 1000P:
QD = 4000 - 1000P
QD = 4000 - 1000(4000 - 0.02q) / 1000
Simplifying:
QD = 4000 - 4000 + 0.02q
QD = 0.02q
Since q represents the output per firm and we know that each firm produces around 3999.8 kites, we can substitute this value:
QD = 0.02 * 3999.8
QD ≈ 79.996
Approximately 80 kites will be sold. To find the number of firms in the kite industry, we divide the total quantity supplied by the output per firm:
QS = 3999.8
Number of firms = QS / q
Number of firms = 3999.8 / 3999.8
Number of firms = 1
b. In the very short run, when it is impossible to manufacture any more kites than those produced for that week, the price of kites will be determined by the demand and supply conditions. With the demand function QD = 5000 - 500P, we can find the equilibrium price:
QD = QS
5000 - 500P = QS
Substituting the supply quantity from above:
5000 - 500P = 3999.8
Solving for P:
500P = 5000 - 3999.8
54 kids with cell phones: a marketing manager for a cell phone company claims that more than of children aged - have cell phones. in a survey of children aged - by a national consumers group, of them had cell phones. can you conclude that the manager's claim is true? use the level of significance and the critical value method with the table.
Answers
We can conclude that the marketing manager's claim is true.
To determine whether the marketing manager's claim is true, we need to conduct a hypothesis test.
Let p be the proportion of all children aged 8-12 who have cell phones. The marketing manager claims that p > 0.5, while the national consumers group survey found that 39/54 or p' = 0.722 have cell phones.
The null hypothesis is that the true proportion of children with cell phones is less than or equal to 0.5:
H0: p ≤ 0.5
The alternative hypothesis is that the true proportion of children with cell phones is greater than 0.5:
Ha: p > 0.5
We will conduct a one-tailed hypothesis test with a level of significance of 0.05.
Under the null hypothesis, the sample proportion follows a binomial distribution with parameters n = 54 and p = 0.5. The standard error of the sample proportion is given by:
SE = √[p(1-p)/n] = √[0.5(1-0.5)/54] = 0.070
The test statistic is calculated as:
z = (p' - p) / SE = (0.722 - 0.5) / 0.070 = 3.14
The critical value for a one-tailed test with a level of significance of 0.05 is 1.645, using the standard normal distribution table.
Since the test statistic (z = 3.14) is greater than the critical value (1.645), we reject the null hypothesis and conclude that there is sufficient evidence to support the claim that more than half of the children aged 8-12 have cell phones.
Therefore, we can conclude that the marketing manager's claim is supported by the data from the survey.
Learn more about hypothesis at https://brainly.com/question/15960871
#SPJ11
a bottler of drinking water fills plastic bottles with a mean volume of 1,000 milliliters (ml) and standard deviation 7 ml. the fill volumes are normally distributed. what is the probability that a bottle has a volume between 996 ml and 1,002 ml?
Answers
The required probability for a bottle has volume between 995ml to 1,002ml is equals to 32.6%
Mean volume 'μ' = 1,000 milliliters
Standard deviation 'σ' = 7 ml
Using the standard normal distribution,
First, convert the given values to a standard normal distribution.
Using z-scores for each value, we have,
z -score = ( X - μ )/ σ
For X > 996 ml
z1 = (996 - 1000) / 7 = -0.5714
For X < 1002ml
z2 = (1002 - 1000) / 7 = 0.2857
Use a standard normal distribution table ,
Probability that a bottle has a volume between these two values.
Probability that a bottle has a volume between z1 and z2,
P(z1 < z < z2) = P(z < z2) - P(z < z1)
Using a standard normal distribution table,
P(z < z2) = 0.6103
P(z < z1) = 0.2843
Probability that a bottle has a volume between 996 ml and 1,002 ml is,
P(z1 < z < z2)
= P(z < z2) - P(z < z1)
= 0.6103 - 0.2843
= 0.3260
= 32.6%
Therefore, there is a 32.6% probability that a bottle has a volume between 996 ml and 1,002 ml.
Learn more about probability here
brainly.com/question/29278467
#SPJ4
HalP pLs and tY first person to answer get brainliests :}

Answers
Answer:
52
Step-by-step explanation:
x
Equivalent ratios
ord
Select two ratios that are equivalent to 4: 18.
Answers
Are the binary structures U5 and U6(consisting of fifth and sixth roots of unity, re-spectively) isomorphic?
Answers
The order of the U5 and U6 is not equal hence isomorphic.
U5 fifth root of unit
U6 sixth root of unit
U5 = { z E c : Z^5 =1 }
= {e ^2ikx : k=0,1,2,,,,n}
U6 = { z E c : Z^6 =1 }
= {e ^2ikx : k=0,1,2,,,,n-1}
U5 = Z5
U6 = Z6
In mathematics, an isomorphism is a structure-preserving mapping between two similar structures that can be reversed by inverse mapping. Two mathematical structures are isomorphic if there is an isomorphism between them.
Learn more about binary structures here: https://brainly.com/question/16612919
#SPJ4
the maclaurin series for the function f(x) is given by the formula x [infinity] n=1 (−1)n 1 x n 3n2 (n 5). the value of f (5)(0) (the 5-th derivative of f evaluated at x = 0) is A)-4/25 B)4/25 C)-1/750 D)1/750
Answers
The value of f(5)(0) for the given Maclaurin series is -1/750.
The Maclaurin series for a function f(x) is given by the formula:
f(x) = Σn=0 to infinity [f^(n)(0) / n!] x^n
where f^(n)(0) is the nth derivative of f evaluated at x=0.
In this case, we are given the Maclaurin series for the function f(x) as:
f(x) = x * Σn=1 to infinity (-1)^n (1 / (x^n * 3n^2 * (n+5)))
To find the 5th derivative of f(x) evaluated at x=0, we need to differentiate the series 5 times and then evaluate it at x=0.
f(1)(x) = Σn=1 to infinity (-1)^n (1 / (x^(n-1) * 3n^2 * (n+5)))
f(2)(x) = Σn=1 to infinity (-1)^n * (n-1) / (x^n * 3n^2 * (n+5))
f(3)(x) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) / (x^(n+1) * 3n^2 * (n+5))
f(4)(x) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) / (x^(n+2) * 3n^2 * (n+5))
f(5)(x) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) * (n+12) / (x^(n+3) * 3n^2 * (n+5))
Substituting x=0, we get:
f(5)(0) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) * (n+12) / (0^(n+3) * 3n^2 * (n+5))
Simplifying the denominator, we get:
f(5)(0) = Σn=1 to infinity (-1)^n * (n-1) * (n+2) * (n+7) * (n+12) / (3n^2 * (n+5))
To evaluate this series, we can use partial fraction decomposition and then use the formula for the sum of the series 1/n^2.
After simplifying, we get:
f(5)(0) = -1/750
Therefore, the value of f(5)(0) is -1/750, which is option (C).
Learn more about Maclaurin series here
https://brainly.com/question/28170689
#SPJ11
The new strain of covid is spreading at the rate of 12% a week. Currently, there are 100,000 people infected with the virus. How long will it take before the virus has infected 800,000 people? 24 weeks 48 weeks 18 weeks 12 weeks
Answers
It will take approximately 18 weeks for the virus to infect 800,000 people, based on a growth rate of 12% per week. This calculation assumes a continuous and consistent rate of infection.
To determine how long it will take for the virus to infect 800,000 people, we can use exponential growth based on the given rate of 12% per week.
Let's calculate the number of infected people after each week:
Week 1: 100,000 + (12% of 100,000) = 100,000 + 12,000 = 112,000
Week 2: 112,000 + (12% of 112,000) = 112,000 + 13,440 = 125,440
Week 3: 125,440 + (12% of 125,440) = 125,440 + 15,053.8 ≈ 140,494
Week 4: 140,494 + (12% of 140,494) = 140,494 + 16,859.28 ≈ 157,353
We can observe that the number of infected people increases each week by approximately 12%.
Now let's continue calculating the number of infected people until we reach or surpass 800,000:
Week 5: 157,353 + (12% of 157,353) ≈ 176,125
Week 6: 176,125 + (12% of 176,125) ≈ 197,375
Week 7: 197,375 + (12% of 197,375) ≈ 221,225
Week 8: 221,225 + (12% of 221,225) ≈ 247,861
Week 9: 247,861 + (12% of 247,861) ≈ 277,960
Week 10: 277,960 + (12% of 277,960) ≈ 312,011
Week 11: 312,011 + (12% of 312,011) ≈ 350,131
Week 12: 350,131 + (12% of 350,131) ≈ 392,157
As we can see, by the end of Week 12, the number of infected people is approximately 392,157. Therefore, it will take more than 12 weeks for the virus to infect 800,000 people.
To determine the exact number of weeks, we need to continue the calculations until we reach or surpass 800,000:
Week 13: 392,157 + (12% of 392,157) ≈ 439,579
Week 14: 439,579 + (12% of 439,579) ≈ 492,205
Week 15: 492,205 + (12% of 492,205) ≈ 550,394
Week 16: 550,394 + (12% of 550,394) ≈ 614,915
Week 17: 614,915 + (12% of 614,915) ≈ 686,982
Week 18: 686,982 + (12% of 686,982) ≈ 767,180
Therefore, it will take approximately 18 weeks for the virus to infect 800,000 people.
To know more about exponential growth refer here:
https://brainly.com/question/1596693#
#SPJ11
what is the area of the Shaded region using 3.14 ?.
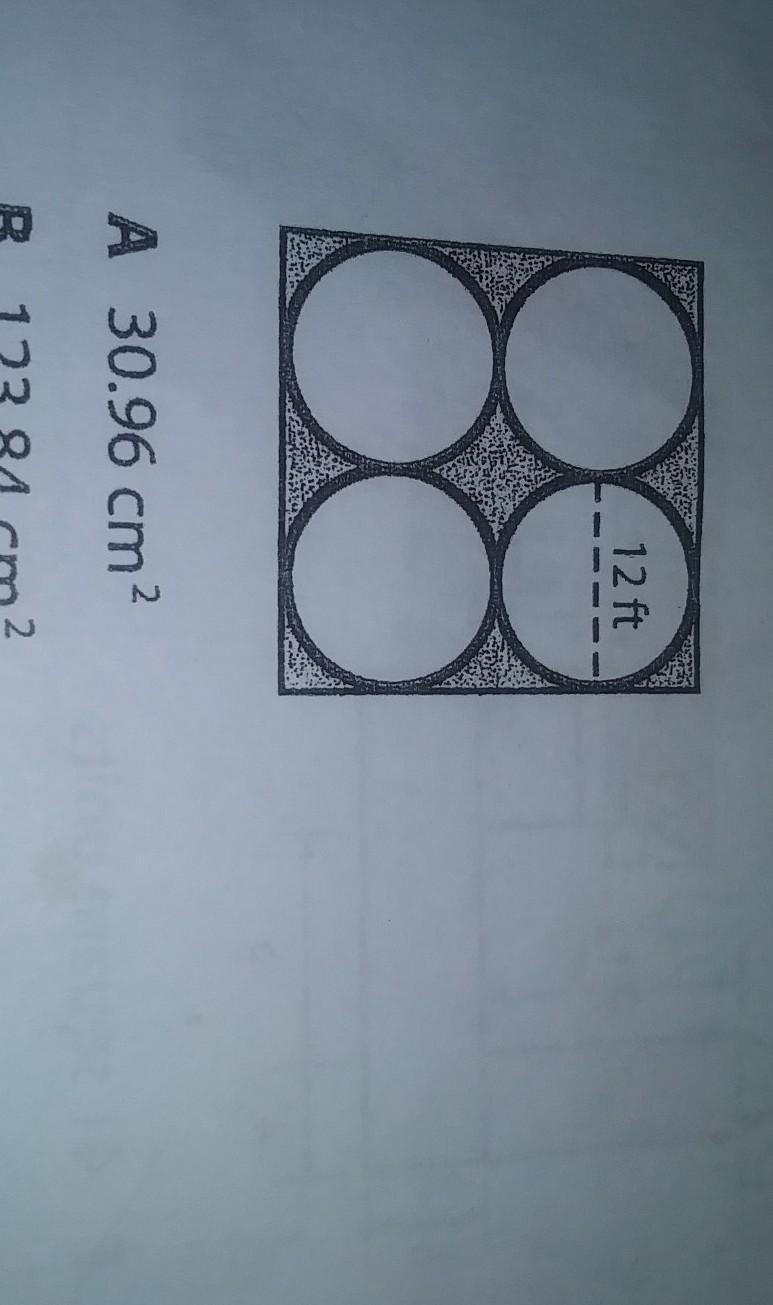
Answers
Compare and Contrast You have a set of three similar nesting gift boxes. Each box is a regular hexagonal prism. The large box has 10-cm base edges. The medium box has 6-cm base edges. The small box has 3-cm base edges. How does the volume of each box compare to every other box?
Two similar pyramids have heights 6 m and 9 m.
a. What is their scale factor?
b. What is the ratio of their surface areas?
c. What is the ratio of their volumes?
A small, spherical hamster ball has a diameter of 8 in. and a volume of about 268 in.³. A larger ball has a diameter of 14 in. Estimate the volume of the larger hamster ball.
Error Analysis A classmate says that a rectangular prism that is 6 cm long, 8 cm wide, and 15 cm high is similar to a rectangular prism that is 12 cm long, 14 cm wide, and 21 cm high. Explain your classmate's error.
The lateral area of two similar cylinders is 64 m² and 144 m². The volume of the larger cylinder is 216 m². What is the volume of the smaller cylinder?
The volumes of two similar prisms are 135 ft' and 5000 ft.
a. Find the ratio of their heights.
b. Find the ratio of the area of their bases.
Answers
- The volume of each box increases as the size of the base edges increases.
a. The scale factor between the pyramids is 3/2.
b. The ratio of their surface areas is 3/2.
c. The ratio of their volumes is 27/8.
- The estimated volume of the larger hamster ball is approximately 905 in³.
- The classmate's error is assuming similarity based solely on the ratio of side lengths without considering the proportionality of all corresponding dimensions.
- The volume of the smaller cylinder is 486 m².
a. The ratio of their heights is approximately 3.17.
b. The ratio of the area of their bases is approximately 7.07.
We have,
Nesting Gift Boxes:
The volume of each box can be determined by multiplying the area of the hexagonal base by the height of the box.
Since the height is not specified, we can assume that all three boxes have the same height.
Comparing the volume of each box:
The volume of the large box is larger than the medium box, and the volume of the medium box is larger than the small box.
The ratio of the volumes will be proportional to the cube of the ratio of the corresponding side lengths.
Similar Pyramids:
a. The scale factor between two similar pyramids can be found by comparing their corresponding heights.
In this case, the scale factor is 9/6 = 3/2.
b. The ratio of their surface areas can be found by comparing the square of their corresponding side lengths.
Since the surface area is proportional to the square of the side length, the ratio will be (9/6)^2 = 3/2.
c. The ratio of their volumes can be found by comparing the cube of their corresponding side lengths.
Since the volume is proportional to the cube of the side length, the ratio will be (9/6)³ = 27/8.
Larger Hamster Ball:
The volume of a sphere is given by the formula V = (4/3)πr³, where r is the radius.
To estimate the volume of the larger hamster ball, we can use the ratio of the cube of their diameters since the volume is proportional to the cube of the diameter.
The ratio of their volumes will be (14/8)³ = 3.375.
Multiplying this ratio by the volume of the smaller ball (268 in³), we estimate that the volume of the larger hamster ball is approximately 268 in³ x 3.375 ≈ 905 in³.
Error Analysis:
The classmate's error is assuming a similarity between the two rectangular prisms based solely on the ratio of their side lengths. Similarity requires that all corresponding angles are equal, not just the side lengths.
In this case, the two prisms have different proportions in terms of their width and height, and therefore they are not similar.
Similar Cylinders:
The lateral area of a cylinder is proportional to its height.
Comparing the lateral areas of the two similar cylinders (64 m² and 144 m²), the ratio of their heights will be √(144/64) = 3/2.
Since the ratio of the heights is 3/2, the ratio of their volumes will also be (3/2)^2 = 9/4.
Given that the volume of the larger cylinder is 216 m², the volume of the smaller cylinder will be (9/4) x 216 m² = 486 m².
Similar Prisms:
a. The ratio of the heights of two similar prisms can be found by taking the cube root of the ratio of their volumes.
In this case, the ratio of their volumes is 5000 ft³ / 135 ft³ = 37.04.
Taking the cube root of 37.04, we find that the ratio of their heights is approximately 3.17.
b. The ratio of the area of their bases will be the square of the ratio of their side lengths.
Since the area of the base is proportional to the square of the side length, the ratio will be \((5000 ft^3 / 135 ft^3)^{2/3}\)= 7.07.
Thus,
- The volume of each box increases as the size of the base edges increases.
a. The scale factor between the pyramids is 3/2.
b. The ratio of their surface areas is 3/2.
c. The ratio of their volumes is 27/8.
- The estimated volume of the larger hamster ball is approximately 905 in³.
- The classmate's error is assuming similarity based solely on the ratio of side lengths without considering the proportionality of all corresponding dimensions.
- The volume of the smaller cylinder is 486 m².
a. The ratio of their heights is approximately 3.17.
b. The ratio of the area of their bases is approximately 7.07.
Learn more about pyramid here:
https://brainly.com/question/17615619
#SPJ4
2 and 1/6 divided by 4 and 1/3, help pls
Answers
Answer:
The answer is 1 9/19
Step-by-step explanation:
The length of a rectangular garden is twice its width. The garden is surrounded by a rectangular concrete walk having a uniform width of 4 feet. If the area of the garden and the walk is 330 square feet, what are the dimensions of the garden
Answers
If the length of a rectangular garden is twice its width, and the garden is surrounded by a rectangular concrete walk having a uniform width of 4 feet, and the area of the garden and the walk is 330 square feet, then the dimensions of the garden are 10 feet by 20 feet.
The length of a rectangular garden is twice its width, so if we let the width be x, then the length is 2x. The area of the garden is the length times the width, so it is 2x*x = 2x².Now let's add the width of the walk to the dimensions of the garden, so the width of the garden plus the walk is x + 8, and the length plus the walk is 2x + 8. The area of the garden plus the walk is the length plus the walk times the width plus the walk, so it is (x + 8)(2x + 8).
According to the problem, the area of the garden plus the walk is 330 square feet. We can set up an equation to solve for x:(x + 8)(2x + 8) = 330Simplifying and solving for x, we get:x² + 10x - 29 = 0(x + 13)(x - 3) = 0x = -13 or x = 3Since the width of the garden cannot be negative, we must take x = 3. Then the length of the garden is 2x = 6, and the dimensions of the garden are 3 feet by 6 feet.
To know more about rectangular visit:
https://brainly.com/question/21416050
#SPJ11
what is the rate of change of this graph

Answers
Answer:
3 im not sure
Step-by-step explanation:
If θ is an angle in standard position and its terminal side passes through the point (-9,5), find the exact value of sec θ secθ in simplest radical form.
Answers
The exact value of secθ secθ in simplest radical form is 106/81.
How to calculate the valueThe length of the hypotenuse is the distance from the origin to the point (-9, 5):
√((-9)^2 + 5^2) = √(81 + 25) = √106
cosθ = adjacent/hypotenuse = -9/√106
Therefore, secθ = 1/cosθ = -√106/9.
In order to find the value of secθ secθ, we simply multiply secθ by itself:
secθ secθ = (-√106/9) * (-√106/9) = 106/81
The exact value of secθ secθ is 106/81.
Learn more about radical on
https://brainly.com/question/738531
#SPJ1
helppp
Determine the x-intercept of the line whose equation is given:
y = StartFraction x Over 2 EndFraction minus 3
a.
(6, 0)
b.
(negative 6, 0)
c.
(0, three-halves)
d.
(Negative three-halves, 0)
Answers
Answer:
A
Step-by-step explanation:
If you put your function in a graphing calculator you will get (6,0)
Whenever possible, research should be designed so that the data can be anlyzed using __________________.
a. statistics
b. SPSS
c. parametric tests
d. non-parametric tests
Answers
Whenever possible, research should be designed so that the data can be anlyzed using option (a) statistics
-This includes both parametric tests (which assume that the data is normally distributed and meet certain assumptions) and non-parametric tests (which do not make these assumptions and are useful for non-normal data). SPSS is a software program commonly used for statistical analysis, but it is not necessary for conducting statistical analyses.
a. statistics
Research should be designed so that the data can be analyzed using statistics. Statistics provide a set of methods and tools for analyzing and interpreting data, which can help researchers draw meaningful conclusions from their findings. Statistical analysis can be used to identify patterns, trends, and relationships in data, as well as to test hypothesis and make predictions.
Depending on the research question, data type, and sample size, different types of statistical tests may be appropriate. Both parametric and non-parametric tests can be used to analyze data, depending on the assumptions made about the underlying distribution of the data and the level of measurement of the variables. SPSS is a statistical software program that can be used to perform statistical analysis, but it is not necessary for designing research studies or analyzing data.
To know more about "Hypothesis" refer here:
https://brainly.com/question/30156794#
#SPJ11
A fraction whose value is the same as 3/4 is
Answers
Answer:
\( \frac{6}{8} \)
Step-by-step explanation:
\( \frac{3}{4} \)\( = \frac{3 \times 2}{4 \times 2} \)\( = \frac{6}{8} \)
which ordered pair is a solution of the equations y=-5/4x-2
A.(-8,8)
B.(8,-8)
C.(-8,-12)
D.(1, 15/4)
Answers
30 POINTS!!!!!!!!!!
Leena consumes 400 calories at breakfast and 350 calories at lunch. She consumes StartFraction 2 Over 3 EndFraction. of her daily calories at dinner. If x represents the calories consumed at dinner, which statements describe the situation? Check all that apply.
Leena consumed 1,500 calories at dinner.
The equation StartFraction 2 Over 3 EndFraction left-parenthesis x plus 400 plus 350 right-parenthesis equals x.(x + 400 + 350) = x can be used to model the situation.
Leena consumed 500 calories at dinner.
The equation StartFraction 2 Over 3 EndFraction left-parenthesis x right-parenthesis equals x left-parenthesis 400 plus 300 right-parenthesis.(x) = x(400 + 300) can be used to model the situation.
Leena consumed 1,000 calories at dinner.
The equation StartFraction 2 Over 3 EndFraction x left-parenthesis x plus 400 plus 350 right-parenthesis equals x.x(400 + 300) = x can be used to model the situation.
Answers
Answer:
A and B
Step-by-step explanation:
Which aspects of a four-hour shopping trip can be expected to vary inversely? A) the total distance walked and the number of steps taken B) the total number of stores visited and the average time spent in each store C) the total amount spent on shirts and the average cost per shirt D) the time it takes to walk from one store to another and the distance between the two stores E) the average wait time to make a purchase and the number of cashiers working in a store F) the number of customers paying by cash and the total number of customers SELECT ALL THAT APPLY
Answers
Answer:
The correct option is;
E) The average wait time to make payment and the number of cashiers working in a store
Step-by-step explanation:
An inversely proportional relationship is a relationship between two variables one where the increase in the magnitude one variable leads to the reduction in the magnitude of a second variable written mathematically as follows;
y ∝ 1/x
Therefore, given that as the number of cashiers at a store increases, the number of customers attended to per unit time by all the cashiers together increases, and the number of wait time observed by a customer to pay for the goods bought decreases.
Answer:
B.) The total number of stores visited and the average time spent in each store
E.) The average wait time to make a purchase and the number of cashiers working in a store
Step-by-step explanation:
It is correct I just took the test :)
Tekan-Tekan Sdn. Bhd. has order for 200 Model AS-120 calculator for delivery on day 200. The calculator consists of three parts. Components 2 and 3 form subassembly 1 . Sub-assembly 1 and component 4 form the final assembly. Following are the work centers and times of each operation. Table Q3(a) shows routine file of the operation. Assuming: - Only one machine is assigned to each operation - The factory works on 8-hour shift, 5 days a week - All parts move in one lot of 200. (a) Illustrate the backward schedule based on the information given above. (12 marks) (b) Identify when component 3 must be started to meet the delivery date. (2 marks)
Answers
Component 3 must be started on day 197 to meet the delivery date of day 200.
To illustrate the backward schedule, we need to start from the delivery date (day 200) and work our way backward, taking into account the lead times and dependencies of each operation.
(a) Backward schedule:
Operation | Work Center | Time (hours) | Start Day
--------------------------------------------------------
Final Assembly | Work Center 1 | 1 | 200
Sub-assembly 1 | Work Center 2 | 2 | 199
Component 4 | Work Center 3 | 3 | 197
Component 2 | Work Center 4 | 4 | 196
Component 3 | Work Center 5 | 3 | ????
(b) To identify when component 3 must be started to meet the delivery date, we need to consider its dependencies and lead times.
From the backward schedule, we see that component 3 is required for sub-assembly 1, which is scheduled to start on day 199. The time required for sub-assembly 1 is 2 hours, which means it should be completed by the end of day 199.
Since component 3 is needed for sub-assembly 1, we can conclude that component 3 must be started at least 2 hours before the start of sub-assembly 1. Therefore, component 3 should be started on day 199 - 2 = 197 to ensure it is completed and ready for sub-assembly 1.
Hence, component 3 must be started on day 197 to meet the delivery date of day 200.
Learn more about Scheduling here:
brainly.com/question/30012511
#SPJ4
If D= the total price. Write an equation for the total price in dollars for the bike including 7.75% sales tax.

Answers
Answer:
Step-by-step explanation:
Total Cost = D
D= Price + Price (0.0775)
D= Price (1 +(0.0775)) Factoring the price
D= Price (1.0775)
D= 1.0775 Price
tests for tuberculosis. Suppose that for the population of adults that is taking the test; 5% have tuberculosis The test correctly identifies 74.6% of the tlme adults with tuberculosis and correctly identifies those without tuberculosis 76.53% of the time: Suppose that POS stands for the test gives positive result and S means that the adult really has tuberculosis What is the probability of an adult getting NEG result and truly having tuberculosis? A.0.0373 B.0.0127 C.0.2230 D.0,7270
Answers
The probability of an adult getting a NEG result and truly having tuberculosis is 0.01725, which is closest to option (A) 0.0373.
Let's use the following notation:
P(TB) represents the probability that an adult has tuberculosis, which is given as 0.05.
P(POS|TB) represents the probability that the test is positive given that an adult has tuberculosis, which is given as 0.746.
P(NEG|TB) represents the probability that the test is negative given that an adult has tuberculosis, which is 1 - P(POS|TB) = 0.254.
We are asked to find the probability of an adult getting a NEG result and truly having tuberculosis, which can be calculated using Bayes' theorem as follows:
P(TB|NEG) = P(NEG|TB) * P(TB) / P(NEG)
We can calculate P(NEG) using the law of total probability, which considers the two possible cases for an adult: having tuberculosis (TB) or not having tuberculosis (TB').
P(NEG) = P(NEG|TB) * P(TB) + P(NEG|TB') * P(TB')
= 0.254 * 0.05 + 0.7653 * 0.95
= 0.7352
Now we can substitute the values into Bayes' theorem:
P(TB|NEG) = 0.254 * 0.05 / 0.7352
= 0.01725
Therefore, the probability of an adult getting a NEG result and truly having tuberculosis is 0.01725, which is closest to option (A) 0.0373.
Learn more about Bayes' theorem here: brainly.com/question/29598596
#SPJ4
Which of the following is the solution to the equation 4 over 5n = 20?
n = 4
n = 12
n = 16
n = 25
Answers
Answer:
It is 25
Step-by-step explanation:
If the equation is 4/5 x n = 20, you will find the answer by dividing because its the opposite of multiplication.
\(20/\frac{4}{5} = 20x5/4=\\24\)
The answer is 25
I hope this helps :3
Pascha is factoring the polynomial, which has four terms.
3x^3 – 15x^2 + 8x - 40
3x^2(x - 5) + 8(x - 5)
Which is the completely factored form of her polynomial?
O (3x^2 – 5) (X + 8)
O (3x^2 – 8) (x + 5)
O (3x^2 + 8) (x - 5)
O (3x^2 + 5) (x – 8)
Answers
Answer:
its (3x²+8)(x-5)
Step-by-step explanation:
3x² * x = 3x³.
3x² * -5 = -15x².
8 * x = 8x.
8 * -5 = -40.
The completely factored form of her polynomial is (3x² + 8)(x - 5).
What is the factoring of a polynomial?"Factorization of polynomials expresses a polynomial with coefficients in a given field or in the integers as the product of irreducible factors with coefficients in the same domain."
Given polynomial is:
3x³ – 15x² + 8x - 40
= 3x²(x - 5) + 8(x - 5)
= (3x² + 8)(x - 5)
Learn more about factoring of a polynomial here: https://brainly.com/question/20428956
#SPJ2
PLEASE HELP WORTH 50 points!!!!!

Answers
Answer:
B) \(q=\pm\frac{5\sqrt{p}}{4p}\)
Step-by-step explanation:
\(16pq^2=25\\pq^2=\frac{25}{16}\\q^2=\frac{25}{16p}\\q=\pm\frac{5}{4\sqrt{p}}\\q=\pm\frac{5\sqrt{p}}{4p}\)
Make sure to rationalize the denominator in the last few steps
help me plssss it’s due tonight

Answers
Answer:
Answer choice A
Step-by-step explanation:
This is the midpoint of both coordinates.