I give Brainliest!!
Using Angle Side Relationship Theorem, use the angle measures to list the side lengths of the triangle in order from longest to shortest. (First you must find the value of angle
AB BC AC

Answers
Answer:
side BCside ABside ACStep-by-step explanation:
list the side lengths of the triangle in order from longest to shortest
from the given triangle.
find angle A∠A = 180 - 65 - 30
∠A = 85
angle side relationship theorem:
In a triangle, the side opposite the larger angle is the longer side
∠A = 85 = side BC∠C = 65 = side AB∠B = 30 = side AC
Related Questions
Which of the following are assumptions underlying the simple linear regression model y = Bo B1x e? Check all that apply The variance of the error term e varies for differing values of x. The error term is a random variable with an expected value of zero. The error term is normally distributed. The error term E follows a chi-square distribution.
Answers
The error term is a random variable with an expected value of zero.2. The error term is normally distributed
The assumptions underlying the simple linear regression model `y = Bo + B1x + e` are: 1.
The variance of the error term e is constant across all values of x.Thus, the assumptions that are underlying the simple linear regression model `y = Bo + B1x + e` are the second and the third options, which are "The error term is normally distributed." and "The variance of the error term e is constant across all values of x." respectively.
Learn more about random variable
https://brainly.com/question/30789758
#SPJ11
Ms. Carlson is planning a dance recital for her students. The maximum duration for the recital is 76 minutes. Group dance numbers last 6 minutes and a solo performance lasts 2 minutes.
Write the inequality in standard form that describes this situation. Use the given numbers and the following variables.

Answers
The inequality that describes this situation will be 6x + 2s ≤ 76
How to compute the inequality?Inequalities are simply created through the connection of two expressions. In this case, it should be noted that the expressions in an inequality are not always equal. Inequalities implies that the expressions are not equal. Here, they are denoted by the symbols ≥ < > ≤.
x = number of group dance numbers
s = number of solo performances
The inequality will be 6x + 2s ≤ 76
This inequality can be read as "the total duration of the group dance numbers (6 minutes per group dance number) plus the total duration of the solo performances (2 minutes per solo performance) is less than or equal to 76 minutes."
Learn more about inequalities on:
https://brainly.com/question/24372553
#SPJ1
The equation for line p can be written as y = 1/4x + 3. Line q includes the point (-1, 5) and is
perpendicular to line p. What is the equation of line q?
Answers
Answer:
\(y=-4x+1\)
Step-by-step explanation:
To get this, use the following steps:
1) Knowing that line q is perpendicular to the line p, the slope of line q must be the negative reciprocal of the slope of line p. Thus the slope is \(-(\frac{1}{4})^{-1} = -4\)
2) To find the equation, plug in the point given:
\(5 = -4(-1) + b\)
\(b = 1\)
3) The equation of line q is thus:
\(y= -4x+1\)
In a single-component pressure-temperature diagram for a pure substance, which of the following phase boundaries will reside at the lowest pressure-temperature conditions?
Sublimation curve
Supercritical curve
Vaporization curve
Fusion (a.k.a. melting) curve
Answers
The sublimation curve will reside at the lowest pressure-temperature conditions in a single-component pressure-temperature diagram for a pure substance.
Explanation: In a pressure-temperature diagram, the sublimation curve represents the phase boundary between the solid and gas phases of a substance. It indicates the conditions at which a substance can undergo sublimation, which is the direct transition from the solid phase to the gas phase without passing through the liquid phase.
At the lowest pressure-temperature conditions, where the pressure and temperature are relatively low, the sublimation curve will be encountered. This is because sublimation generally occurs at lower pressures and temperatures compared to other phase transitions.
In contrast, the vaporization curve represents the phase boundary between the liquid and gas phases, and the fusion (or melting) curve represents the phase boundary between the solid and liquid phases. These curves generally occur at higher pressure-temperature conditions compared to the sublimation curve.
The supercritical curve represents the region where the substance exists as a supercritical fluid, which is a state above the critical temperature and pressure. This curve is typically found at higher pressure and temperature conditions compared to the sublimation curve.
Learn more about curve here:
https://brainly.com/question/31012623
#SPJ11
where are module variables, parameters, and temporary variables introduced and initialized in a program?
Answers
Answer:
Step-by-step explanation:
Module variables, parameters, and temporary variables are introduced and initialized in different parts of a program. Module variables are typically declared at the beginning of a module or file and are accessible throughout that module.
Parameters are introduced when defining functions or subroutines, serving as placeholders for values that will be passed into the function. Temporary variables are created within the scope of a function or subroutine to store intermediate values during the execution of the program.
Module variables are usually declared at the beginning of a module or file, outside of any specific function or subroutine. They are initialized with a value or left uninitialized, depending on the programming language. Module variables can be accessed and modified by any function or subroutine within the module, making them useful for storing data that needs to be shared across different parts of the program.
Parameters, on the other hand, are introduced when defining functions or subroutines. They are listed within the parentheses after the function/subroutine name and are separated by commas if there are multiple parameters. When a function is called, values are passed into these parameters, which then serve as variables within the function's scope. Parameters are initialized with the values provided at the function call, allowing the function to operate on different input data each time it is invoked.
Temporary variables are typically created within the body of a function or subroutine to store intermediate values during program execution. They are declared and initialized as needed within the function's block of code. Temporary variables are used for calculations, storage, or transformations of data within the function and are usually not accessible outside of the function's scope. Once the function completes its execution, the temporary variables are no longer available in memory.
Learn more about Module Variables here :
brainly.com/question/28320134
#SPJ11
Who knows how to do this I TRULY NEED HELP

Answers
Answer: The answer is #3
Step-by-step explanation:
Solve the first order linear differential equation dy/ dx +3y=2x+8 y(0)=0 y(x)=
Answers
The general solution to the first-order linear differential equation dy/dx + 3y = 2x + 8 is y(x) = x^2 + 8x.
To obtain the general solution, we start by rearranging the equation to the standard form of a linear first-order differential equation:
dy/dx + 3y = 2x + 8
The integrating factor μ(x) is given by
μ(x) = e^(∫3 dx) = e^(3x).
We multiply both sides of the equation by μ(x) to make the left-hand side exact:
e^(3x)dy/dx + 3e^(3x)y = 2xe^(3x) + 8e^(3x)
Applying the product rule, we can rewrite the left-hand side as d(ye^(3x))/dx = 2xe^(3x) + 8e^(3x)
Integrating both sides with respect to x, we have
∫d(ye^(3x))/dx dx = ∫(2xe^(3x) + 8e^(3x)) dx
Simplifying, we get ye^(3x) = ∫(2xe^(3x) + 8e^(3x)) dx
Integrating and applying the constant of integration, we have
ye^(3x) = x^2e^(3x) + 8xe^(3x) + C.
Dividing both sides by e^(3x), we obtain
y(x) = x^2 + 8x + Ce^(-3x).
Since y(0) = 0, we can substitute this initial condition into the equation to find the specific value of C:
0 = 0 + 0 + Ce^(-3*0).
Solving for C, we have C = 0.
Therefore, the particular solution satisfying the initial condition is y(x) = x^2 + 8x.
Learn more about differential equation here:
brainly.com/question/33433874
#SPJ11
find the taylor polynomials p1, ..., p4 centered at a0 for f(x).
Answers
The Taylor polynomials P1, P2, P3, and P4 centered at a0 for f(x) are given as:P1(x) = 1P2(x) = 1 - x²/2!P3(x) = 1 - x²/2! + x⁴/4!P4(x) = 1 - x²/2! + x⁴/4! - x⁶/6!
We will apply the Taylor's theorem formula, which is supplied as follows, to determine the Taylor polynomials P1, P2, P3, and P4 centred at a0 for f(x) in the given question:f'(a)(x-a)/1 = f(x) = f(a) + f'(a)! + f''(a)(x-a)²/2! + ... + fⁿ(a)(x-a)ⁿ/n!We have f(0) = 1f'(0) = 0f''(0) = -1f'''(0) = 0f4(0) = 1 for f(x) = cos(x) at x = 0.We can get the following polynomial expressions by using these values in the Taylor's theorem formula:P1(x) = 1P2(x) = 1 - x²/2!P3(x) = 1 - x²/2! + x⁴/4!P4(x) = 1 - x²/2! + x⁴/4! - x⁶/6!Consequently, the Taylor polynomials P1, P2, P3, and P4 for f(x) are provided as follows:P1(x) = 1P2(x) = 1 - x²/2!P3(x) = 1 - x²/2! + x⁴/4!P4(x) = 1 - x²/2! + x⁴/4! - x⁶/6!
To know more about Taylor polynomials Visit:
https://brainly.com/question/30481013
#SPJ11
4
2
2468
-10
2 4
A. y = (x+4)³(x + 2)(x - 1)
C. y = (x+4)(x + 2)(x - 1)³
Identify the equation
for the graph.
B. y = (x+4)(x + 2)²(x - 1)
D. y = (x+4)(x + 2)(x-1)

Answers
Answer:
D
Step-by-step explanation:
given the roots of a polynomial x = a, x = b , x = c
then the factors are (x - a) , (x - b) , (x - c)
the polynomial is then the product of the factors
y = (x - a)(x - b)(x - c)
here the roots , where the graph crosses the x- axis, are
x = - 4 , x = - 2 , x = 1
then the factors are
(x - (- 4) ) , (x - (- 2) ) , (x - 1) , that is
(x + 4) , (x + 2) , (x - 1)
Then
y = (x + 4)(x + 2)(x - 1)
Find the solution of the initial value problem y" + 4y = t^2 + 2e^t, y(0) = 0, y' (0) =1
Answers
The solution to the initial value problem is: y(t) = -1/2 cos(2t) + 1/2 t² +\(e^t\)
To solve the initial value problem y" + 4y = t² + \(2e^{t}\), y(0) = 0, y' (0) = 1, we first find the complementary function (CF) and the particular integral (PI), and then combine them to get the general solution.
Step 1: Find the complementary function
The characteristic equation is r² + 4 = 0, which has roots r = ±2i. Therefore, the complementary function is:
yCF(t) = c1 cos(2t) + c2 sin(2t)
where c1 and c2 are constants determined by the initial conditions.
Step 2: Find the particular integral
We look for a particular integral of the form:
yPI(t) = at² + b + \(ce^{t}\)
where a, b, and c are constants to be determined.
Substituting yPI(t) into the differential equation, we get:
2a + 2c = t² + \(2e^t\)
Solving for a and c, we get:
a = 1/2
c = \(e^t\)
Substituting these values into yPI(t), we get:
yPI(t) = 1/2 t² + \(e^t\)
Step 3: Find the general solution
The general solution is the sum of the complementary function and the particular integral:
y(t) = yCF(t) + yPI(t) = c1 cos(2t) + c2 sin(2t) + 1/2 t² + \(e^t\)
Step 4: Find the constants c1 and c2 using the initial conditions
Using the initial condition y(0) = 0, we get:
c1 + 1/2 = 0
c1 = -1/2
Using the initial condition y'(0) = 1, we get:
2c2 + 1 = 1
c2 = 0
Therefore, the solution to the initial value problem is:
y(t) = -1/2 cos(2t) + 1/2 t² +\(e^t\)
To know more about complementary function refer here:
https://brainly.com/question/29083802
#SPJ11
this graph represents the maximum number of children that are allowed on a field trip depending on the number of adults present to supervise. a trip is allowing for a maximum of 12 children. how many adults will be present? enter your answer in the box.
Answers
Based on the given information, the graph represents the relationship between the number of adults present and the maximum number of children allowed on a field trip. Since the trip is allowing for a maximum of 12 children, we will analyze the graph to determine how many adults will be present.
Without the graph, we cannot provide the exact number of adults needed for 12 children. However, once you have the graph in front of you, simply locate the point on the graph where the number of children allowed (y-axis) is equal to 12. Then, trace the point horizontally to the corresponding number of adults on the x-axis. This will give you the number of adults required to supervise the 12 children during the field trip.
Remember to follow any guidelines or ratios that may be established by your school or organization regarding adult-to-child ratios on field trips, as this can impact the number of adults needed for the trip.
this graph represents the maximum number of children that are allowed on a field trip depending on the number of adults present to supervise. a trip is allowing for a maximum of 12 children. how many adults will be present? enter your answer in the box.
To learn more about graph : brainly.com/question/17267403
#SPJ11
HELP ME!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
H
Step-by-step explanation:
If they are similar that means that they are racially the same so just divide 60 by 84 to find the rate and then multiply the rate by 210 to get your answer
which of the following is a factor of 12x2 − 4x − 1?
Answers
To find the factors of the expression 12x^2 - 4x - 1, we can use the factor theorem. The factor theorem states that if a polynomial expression evaluates to zero when a certain value is substituted for the variable, then that value is a factor of the polynomial.
To determine if a certain value is a factor of the expression, we can use synthetic division. Synthetic division involves dividing the polynomial expression by the possible factor to check if the remainder is zero. If the remainder is zero, then the value is a factor.
Let's start by checking if x = 1 is a factor of the expression:
1 | 12 - 4 - 1
| 12 8
|____________
12 8 7
Since the remainder is not zero, x = 1 is not a factor of the expression.
Next, let's check if x = -1 is a factor of the expression:
-1 | 12 - 4 - 1
| -12 16
|____________
12 -16 15
Again, the remainder is not zero, so x = -1 is not a factor of the expression.
Now, let's check if x = 2 is a factor of the expression:
2 | 12 - 4 - 1
| 24 40
|____________
12 20 39
Once again, the remainder is not zero, so x = 2 is not a factor of the expression.
Finally, let's check if x = -2 is a factor of the expression:
-2 | 12 - 4 - 1
| -24 56
|____________
12 -28 55
As we can see, the remainder is not zero, so x = -2 is not a factor of the expression.
After checking all the possible factors, we can conclude that none of the values tested (1, -1, 2, -2) are factors of the expression 12x^2 - 4x - 1.
to know more about factors here:
brainly.com/question/30517179
#SPJ11
arrange the steps in the correct order to compute 3^302 mod 11.3302 32 330091 9 (mod 5) 3300(37515 (mod 5) 34 E1 (mod )2 3mod 5 4
Answers
Answer:
3^302 mod 11 = 9.
Step-by-step explanation:
The correct order to compute 3^302 mod 11 is:
Find the remainder of 302 divided by 10 using modular arithmetic: 302 mod 10 = 2.
Use Euler's totient theorem to find the remainder of 11^(10-1) divided by 10: 11^(10-1) mod 10 = 1.
Raise 3 to the power of the remainder from step 1: 3^2 = 9.
Divide the result from step 3 by the result from step 2: 9/1 = 9.
Take the remainder of the result from step 4 divided by 11 using modular arithmetic: 9 mod 11 = 9.
Therefore, 3^302 mod 11 = 9.
To know more about remainder refer here
https://brainly.com/question/30302805#
#SPJ11
describe how to convert decimal numbers to their binary representations, using the amazing binari as an exampl
Answers
Convert decimal numbers to their binary representations suppose 112 binary representation is 1110000.
Convert decimal numbers to their binary representations:
we can simply convert decimal to binary by simply dividing by 2 and remainder is noted and continuing this until the end of the number and writing the result in reverse order we get binary values.
example:
112 remainder
112/2 = 56 0
56/2 = 28 0
28/2 = 14 0
14/2 = 7 0
7/2 = 3 1
3/2 = 1 1
1/2 = 0 1
write the remainder in reverse order.
Binary = 1110000
Learn more about the decimal here:
https://brainly.com/question/548650
#SPJ1
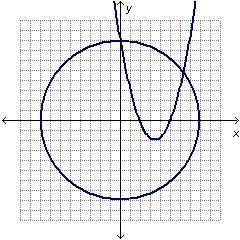
How many solutions exist for the system of equations in the graph?
Answers
Answer:
Two solutions
Step-by-step explanation:
The number of points of intersections represents the number of solutions to the system of equations. Since the parabola intersects the circle at two points, there are two solutions to the circle.
Furthermore, these two points of intersection are exactly the solutions to the system of equations. Finding the coordinates of the points of intersection will give you the solutions to the system of equations.
I need another answer asap! Please and thank you if you answer this and you will get 15 points! So what is the answer to this question? Dax is buying coffee for 5
people in his office. He also leaves a $2.00
tip for the barista.
If his total, with tip, is $18.25,
how much is each cup of coffee, not including the tip?
Enter your answer as a decimal, like this: 42.53
Answers
Answer:
3.25
Step-by-step explanation:
total 18.25 - 2.00 tip = 16.25
16.25/5=3.25
90 to the nearest tenth
Answers
Answer:
90
Step-by-step explanation:
90 has 0 ones so it is already rounded.
Answer:
90
Step-by-step explanation:
Hey there!
Well 90.000 to the nearest tenth is just 90 because there is decimal places to round.
Hope this helps :)
Find the area K of the triangle
Find the area \( K \) of the triangle. \( K= \) square-units (Round to two decimal p aces as neoded.)
Answers
To find the area \( K \) of a triangle, we need to know the lengths of its base and height. The first paragraph provides a summary of the approach, while the second paragraph explains the process in detail.
To find the area \( K \) of a triangle, we can use the formula:
\( K = \frac{1}{2} \times \text{base} \times \text{height} \)
The base of a triangle is the length of one of its sides, and the height is the perpendicular distance from the base to the opposite vertex.
If the base and height are given, we can simply substitute their values into the formula and calculate the area \( K \). However, if the base and height are not provided directly, we need additional information about the triangle, such as the lengths of its sides or angles, to determine the base and height.
Once we have the base and height values, we can substitute them into the formula and evaluate the expression to find the area \( K \). Make sure to round the result to the desired number of decimal places, as specified in the question.
know more about area of the triangle :brainly.com/question/24865193
#SPJ11
To find the area \( K \) of a triangle, we need to know the lengths of its base and height Once we have the base and height values, we can substitute them into the formula and evaluate the expression to find the area \( K \)..
To find the area \( K \) of a triangle, we can use the formula:
\( K = \frac{1}{2} \times \text{base} \times \text{height} \)
The base of a triangle is the length of one of its sides, and the height is the perpendicular distance from the base to the opposite vertex.
If the base and height are given, we can simply substitute their values into the formula and calculate the area \( K \). However, if the base and height are not provided directly, we need additional information about the triangle, such as the lengths of its sides or angles, to determine the base and height.
Once we have the base and height values, we can substitute them into the formula and evaluate the expression to find the area \( K \). Make sure to round the result to the desired number of decimal places, as specified in the question.
know more about area of the triangle :brainly.com/question/24865193
#SPJ11
He height in meters of a model rocket on a particular launch can be modeled by the equation h(t) = −4. 9t2 + 102t + 100, where t is the time in seconds after its engine burns out 100 m above the ground
Answers
The height will be 600 meters at the times:
t = 7.9 seconds
t = 12.9 seconds
How to find the time?We know that the height is modeled by the quadratic function:
h = -4.9t² + 102t + 100
We want to find the value of t such that the height is 600m. then we need to solve the quadratic equation:
600 = -4.9t² + 102t + 100
We can rewrite that to get:
-4.9t² + 102t + 100 - 600 = 0
-4.9t² + 102t - 500 = 0
Using the quadratic formula we will get the solutions:
\(t = \frac{-102 \pm \sqrt{102^2 - 4*-4.9*-500} }{2*-4.9} \\t = \frac{-102 \pm 24.6 }{-9.8}\)
The first time at which the height is 600 meters is:
t = (-102 + 24.6)/-9.8 = 7.9 seconds
The second time is:
t = (-102 - 24.6)/-9.8 = 12.9 seconds
Learn more about quadratic functions at:
https://brainly.com/question/1214333
#SPJ4
Complete question:
"The height above the ground in meters of a model rocket on a particular launch can be
modeled by the equation h = -4.9t² + 102t + 100, where t is the time in seconds after its engine
burns out 100 m above the ground. Will the rocket reach a height of 600 m?"
please answer question with explanation

Answers
Answer:
Domain: \(\{x|x\in\mathbb{R}\}\)
Range: \(\{y|y\in\mathbb{R},y\leq -2\}\)
Step-by-step explanation:
The domain is the span of x-values the graph covers.
The range is the span of y-values the graph covers.
The given graph is a quadratic. We can see that the x-values will extend infinitely in both directions.
Thus, the domain is all real numbers.
In set notation, this is:
\(\{x|x\in\mathbb{R}\}\)
From the graph, we can see that the maximum value is y=-2. The graph won't ever go above this.
So, the range is all real numbers less than or equal to -2.
In interval notation, this is:
\(\{y|y\in\mathbb{R},y\leq -2\}\)
And we are done :)
Which statement is true about the value of |-5|? It is the distance that -5 is form 0 on the number line. It is the distance that -5 from 5 on the number line. It is less than 5. It is greater than 5.
Answers
Answer: It is the distance that -5 is form 0 on the number line
Step-by-step explanation:
We can define the absolute value of any number:
IxI as:
"The distance between the point x and the origin in the coordinate axis"
If we are in one dimension, x is just a value, and the coordinate axis will be a number line.
Then we could rewrite this as:
"is the distance between the value x and the 0 in the number line"
So:
IxI = x if x > 0
IxI = -x if x < 0.
Then:
I -5 I
Is the distance between the number -5, and the 0 in the number line, and this is:
I - 5 I = 5.
The correct option is:
"It is the distance that -5 is form 0 on the number line"
Answer:
Answer: It is the distance that -5 is form 0 on the number line
Step-by-step explanation:
Change the word phrase to an algebraic expression. Use x to represent the number. The product of 9 and two more than a number
Answers
The algebraic expression for "The product of 9 and two more than a number" is 9(x + 2).
In the given word phrase, "a number" is represented by the variable x. The phrase "two more than a number" can be translated as x + 2 since we add 2 to the number x. The phrase "the product of 9 and two more than a number" indicates that we need to multiply 9 by the value obtained from x + 2. Therefore, the algebraic expression for this word phrase is 9(x + 2).
"A number": This is represented by the variable x, which can take any value.
"Two more than a number": This means adding 2 to the number represented by x. So, we have x + 2.
"The product of 9 and two more than a number": This indicates that we need to multiply 9 by the value obtained from step 2, which is x + 2. Therefore, the algebraic expression becomes 9(x + 2).
In summary, the phrase "The product of 9 and two more than a number" can be algebraically expressed as 9(x + 2), where x represents the number.
Learn more about algebraic expression:
https://brainly.com/question/4344214
#SPJ11
For every 1 sheet of paper you have 4 markers. You have 10 sheets of paper. How many markers do you have?
Answers
you have 40 markers........
\(\sf Solve\: the\: following:-\)
\(\sf 16-2t=t+9+4t\)
\(\sf THANKS! :)\)
Answers
Step-by-step explanation:
\(\sf 16-2t=t+9+4t \\ \: \: \: \: \: \: \: \: \: \: \: \:16 = 9 + 5t + 2t \\16 - 9=7t \\ 7t = 7 \\ t = \frac{7}{7} \\ t = 1\)
t=1
Answer:
solution given:
16-2t=t+9+4t
keeping like terms on one side.
16-9=t+4t+2t
7=7t
dividing both side by 7,we get
7/7=7t/7
we get t=1
Step-by-step explanation:
The cost of renting a car for one day is $39 plus 15 cents per mile driven. In a graph of the situation, what does the cost per mile driven represent?
Answers
Answer:
It will represent the slope of the graph
Step-by-step explanation:
Here, we are interested in getting what the cost per mile driven represent
From the information, we can represent the cost as;
C = 15d + 39
In this case we have a representation of the cost using the fixed daily cost(y-intercept) and the cost depending on the number of miles driven which will change based on the number of miles.
Since it is changing, it represents the slope of the function for cost
There are 20 beetles in an area of rainforest. The number of beetles is expected to increase by 66% every year compared to the year before. a) How many beetles are expected to be in the area of rainforest in 5 years' time? b) How many beetles are expected to be in the area of rainforest in 20 years' time? Round your answers to the nearest 100.
Answers
Answer: Your welcome!
Step-by-step explanation:
a) In 5 years' time, there are expected to be 136 beetles in the area of rainforest (20 * 1.66^5 ≈ 135.9, rounded to 136).
b) In 20 years' time, there are expected to be 8,000 beetles in the area of rainforest (20 * 1.66^20 ≈ 8,002.2, rounded to 8,000).
Helpy helps me with this question

Answers
Answer:
it's the third one cuz the rest aren't divisible by 5:00 because the five usually goes up by then by fives then zeros so the end since it's a zero it's divisible by five
Answer:#3 5990
Step-by-step explanation:
5 10 15 20 25 the others dont have a five or a zero at the end
Which of these is not a geometric sequence? 3, 6, 12, 24, ... 250, 50, 10, 2, .... 5, 15, 45, 135, ... 4, 12, 20, 28, ...
Answers
250, 50, 10, 2 is not a geometric sequence
Step-by-step explanation:
It's the only one that doesnt make sence.
Answer:
4, 12, 20, 28
Step-by-step explanation:
The 1st one has the pattern of 2x
3 * 2 = 6
6 * 2 = 12
12 * 2 = 24
Everything in this sequence is true
The 2nd one has the pattern of divided by 5
250/5 = 50
50/5 = 10
10/5 = 2
The 2nd one is true
The 3rd one has the pattern of 3x
5 * 3 = 15
15 * 3 = 45
45 * 3 = 135
The 3rd one is true
The 4th one however, I don't seem to see a pattern
4 * 3 = 12
But...
12 * 3 ≠ 20
20 * 3 ≠ 28
Which makes it false
Hope this helps!!!
A deposit of $2,000 is made in a trust fund that pays 5.5% interest, compounded continuously. It is specified that the balance will be given to the college from which the donor graduated after the money has earned interest for 30 years. How much will the college receive? (Round your answer to the nearest cent.)
Answers
What is given?
(A)mount = ?
(P)rincipal = $2000
e = 2.7183 (always)
(r)ate = .05 (turn into decimal)
(t)imd = 20 years
Plug into formula:
A = 2000*2.7183^(.05*20)
A = $5436.60