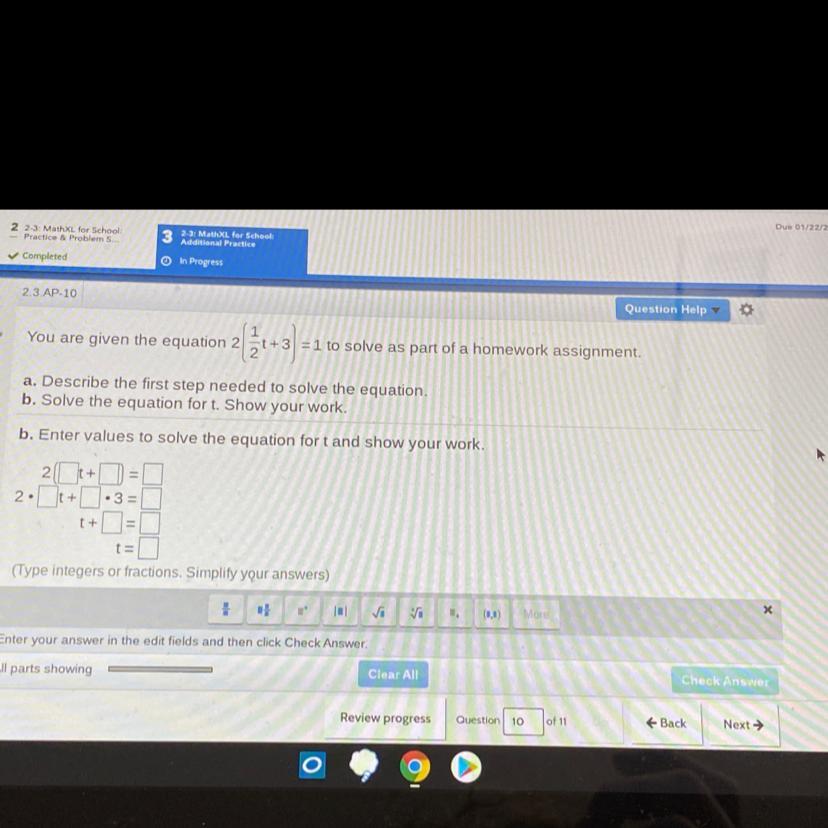
Answers
Answer:
2{\(\frac{1}2}\)t+3}=1
2\(\frac{1}{2}\)t+2 * 3=1
t+6=1
t=-5
Step-by-step explanation:
2{\(\frac{1}2}\)t+3}=1
2\(\frac{1}{2}\)t+2 * 3=1
t+6=1
t=-5
Related Questions
(-9.5) to the power of 0
Answers
What is the equation in point-slope form for the line parallel to y=5x-4 that contains p(-6,1)
Answers
Answer:
\(\displaystyle{y-1=5(x+6)}\)
Step-by-step explanation:
A point-slope form is written in the equation of \(\displaystyle{y-y_1=m(x-x_1)}\). Where \(\displaystyle{(x_1,y_1)}\) is a coordinate point and \(\displaystyle{m}\) is slope.
The definition of parallel is to both lines have same slope. The given line equation has slope of 5. Therefore, we can write the equation in point-slope form as:
\(\displaystyle{y-y_1=5(x-x_1)}\)
Next, we are also given the point p(-6,1). Substitute \(\displaystyle{x_1}\) = -6 and \(\displaystyle{y_1}\) = 1 in:
\(\displaystyle{y-1=5[x-(-6)]}\\\\\displaystyle{y-1=5(x+6)}\)
Hence, the line equation that’s parallel to y = 5x - 4 and passes through a point (-6,1) is y - 1 = 5(x + 6)
Answer:
y - 1 = 5 ( x + 6 )
Step-by-step explanation:
We know that when two lines are parallel the slope of both lines is equal.The formula that we use to find an equation of a line is y = m x + cHere,
m ⇒ slope
Now let us take a look at the given equation which is already drawn.y = 5x - 4 ← equation of the old line
Now it is clear to us that,
m ⇒ slope of the line ⇒ 5
c ⇒ y-intercept ⇒ -4
Therefore, the slope of the new line also will be 5.That is, m = 5
The question asked us to write the equation in point-slope form.The formula to write the equation in the line in point-slope form is :y - y₁ = m ( x - x₁ ).
Here,m = slope
Also, we can use the given coordinates to write the equation in point-slope form( -6 , 1 ) ⇔ ( x₁ , y₁ )
So, to find the equation of the new line we can replace m, y₁ & x₁ with 5, 1 & -6 respectively.Let us solve this now
y - y₁ = m ( x - x₁ )
y - 1 = 5 ( x - ( -6) )
y - 1 = 5 ( x + 6 )
And now let us write the equation of the new line in point - slope form.y - 1 = 5 ( x + 6 )
A Bayesian network on N variables is a complete binary tree, i.e all internal nodes have one edge coming into the node from its parent and exactly two edges leading out into its children. The root node has exactly two edges coming out of it, and each leaf node has exactly one edge leading into it. If each node models a binary random variable, calculate the total number of non-redundant parameters in the network. What is the total number of non-redundant parameters in the unfactored joint probability distribution of all the N variables? Show all steps in your calculation. [6 Marks]
Answers
A complete binary tree is a Bayesian network on N variable, which contains non-redundant parameters. The total number of non-redundant parameters is found using the formula 2 × (N − 1).
A Bayesian network on N variables can be represented as a complete binary tree. This means that all internal nodes have one edge that comes into the node from its parent and exactly two edges leading out into its children. The root node has exactly two edges coming out of it, and each leaf node has exactly one edge leading into it.
Each node models a binary random variable, and the network contains non-redundant parameters. To find the total number of non-redundant parameters, we can use the formula 2 × (N − 1). This is because each internal node has two children and therefore contributes two parameters to the network.
However, the root node only has one parent, and the leaf nodes do not have any children. Therefore, we subtract one from the total number of nodes to account for the root node and subtract the number of leaf nodes to account for the fact that they only have one parent.
The resulting formula is 2 × (N − 1).The total number of non-redundant parameters in the unfactored joint probability distribution of all the N variables can be calculated by taking the product of the number of possible values for each variable.
Subtracting one for each variable to account for the fact that the probabilities must sum to one, and subtracting the number of non-redundant parameters in the Bayesian network. This is because the unfactored joint probability distribution contains all the probabilities for all possible combinations of the N variables, and therefore contains more information than the Bayesian network, which only contains conditional probabilities.
To know more about variable refer here:
https://brainly.com/question/15078630
#SPJ11
Would f(x) be the answer for both and how do you graph the g(x) table graph. What I have to solve for is on top in bold. I am asking for number 12
Algerba 1

Answers
The graph of f(x)=√x+3+2 is shifted 3 units up and 2 units to the right from the parent graph of f(x)=√x.
We have,
Graph is a type of data structure that consists of a set of nodes (also called vertices) and edges. Each node is connected to other nodes by edges. Graphs are used to represent networks of communication, data organization, computational devices, the flow of computation, etc. They are also very useful for visualizing relationships between data points in a variety of fields.
The translation of the parent graph of f(x)=√x+3+2 is a vertical shift upward 3 units, followed by a horizontal shift to the right 2 units. This is represented by the bold line in the graph. In terms of the equation, the translation is represented by the addition of the 3 and the 2 to the function. The 3 causes the graph to shift vertically upward and the 2 causes the graph to shift horizontally to the right. As a result, the graph of f(x)=√x+3+2 is shifted 3 units up and 2 units to the right from the parent graph of f(x)=√x.
To know more about graph click-
brainly.com/question/19040584
#SPJ1
complete question:
Below, the graph of f(x) = √x +3 + 2 is sketched in bold. Its parent function f(x)=√x is represented
by the thin curve.
1) Describe the
translation of the parent
graph.
2) How does the translation relate to the equation?
please answer will give brainliest

Answers
Answer: 29152332 ≡ 0 (mod 3)
Step-by-step explanation:
In modular arithmetic, there is the form a ≡ b (mod m) where b is the remainder.
To solve this problem, we want to divide 29152332 by 3 and find the remainder.
29152332 ÷ 3 = 9717444
Since we get an integer with no remainder, we know the answer is 29152332 ≡ 0 (mod 3).
Lines AB and CD are parallel. Determine the measures of the three angles in the diagram

Answers
Answer:
Step-by-step explanation:

Help with some of my homework, please and thank you

Answers
Area = length x width
Substitute in the values & expressions you know:
(12m + 18) = length x 6
Divide both sides of the equation by 6:
(12m + 18)/6 = length
2m + 3 = length
Answer:
C is right
Step-by-step explanation:
:))
Corinne is making a juice drink from pineapple juice and orange juice
in a ratio 5:3.
- pineapple juice costs £4.70 for 5 litres
- orange juice costs £2.50 for 2 litres
- Corinne makes 32 litres. How much does this
cost her?
Answers
£70.08 is the answer.
Answer:
interesting
you play cod
I don't believe it
The lengths of two sides of a triangle are shown.
Side 1: 8x2 − 5x − 2
Side 2: 7x − x2 + 3
The perimeter of the triangle is 4x3 − 3x2 + 2x − 6.
Part A: What is the total length of the two sides, 1 and 2, of the triangle? Show your work. (4 points)
Part B: What is the length of the third side of the triangle? Show your work. (4 points)
Part C: Do the answers for Part A and Part B show that the polynomials are closed under addition and subtraction? Justify your answer. (2 points)
Answers
Answer:
To find the total length of the two sides, we simply add them together:
Total length = Side 1 + Side 2
Total length = (8x^2 - 5x - 2) + (7x - x^2 + 3)
Total length = -x^2 + 8x^2 - 5x + 7x - 2 + 3
Total length = 7x^2 + 2x + 1
Therefore, the total length of the two sides of the triangle is 7x^2 + 2x + 1.
Step-by-step explanation:
To find the length of the third side of the triangle, we need to use the formula for the perimeter of a triangle:
Perimeter = Side 1 + Side 2 + Side 3
We are given the perimeter of the triangle as 4x^3 - 3x^2 + 2x - 6 and we know the lengths of Side 1 and Side 2. Therefore, we can rewrite the formula as:
4x^3 - 3x^2 + 2x - 6 = (8x^2 - 5x - 2) + (7x - x^2 + 3) + Side 3
Simplifying the right-hand side:
4x^3 - 3x^2 + 2x - 6 = 7x^2 + 2x + 1 + Side 3
Side 3 = 4x^3 - 3x^2 + 2x - 6 - 7x^2 - 2x - 1
Simplifying further:
Side 3 = 4x^3 - 7x^2 - x - 7
Therefore, the length of the third side of the triangle is 4x^3 - 7x^2 - x - 7.
Yes, the answers for Part A and Part B show that the polynomials are closed under addition and subtraction.
Closure under addition means that when two polynomials are added, the result is also a polynomial. In Part A, we added the two polynomials 8x^2 - 5x - 2 and 7x - x^2 + 3 to get the total length of the two sides of the triangle, which is 7x^2 + 2x + 1. Since the total length is also a polynomial, this shows that the polynomials are closed under addition.
Closure under subtraction means that when one polynomial is subtracted from another polynomial, the result is also a polynomial. In Part B, we subtracted the two polynomials 8x^2 - 5x - 2 and 7x - x^2 + 3 from the given perimeter of the triangle, 4x^3 - 3x^2 + 2x - 6, to get the length of the third side of the triangle, which is 4x^3 - 7x^2 - x - 7. Since the length of the third side is also a polynomial, this shows that the polynomials are closed under subtraction.
Therefore, the answers for Part A and Part B demonstrate that the polynomials are closed under addition and subtraction.
a church has 7 bells in its bell tower. before each church service 3 bells are rung in sequence. no bell is rung more than once. how many sequences are there?
Answers
There are 210 sequences for 7 church bells to rung with the given conditions. Using permutations, the required number of sequences is calculated.
What are permutations?A sequence or arrangement that can be framed by taking some or all of a finite set of things (or objects) is called a permutation.
The formula for finding the number of such arrangements is,
ⁿPₓ = n!/(n - x)!
Calculation:It is given that, a church's bell tower has 7 bells. 3 of them will ring in a sequence before each service and no bell is rung more than once.
So, the number of sequences that the bells will form is calculated by using the permutations formula. I.e., ⁿPₓ = n!/(n - x)!
Here, n = 7; x = 3
Then,
ⁿPₓ = n!/(n - x)! ⇒ ⁷P₃ = 7!/(7 - 3)! = 7!/4!
⇒ ⁷P₃ = (7 × 6 × 5 × 4!)/4! = 7 × 6 × 5 = 210
Therefore, there are 210 sequences for ringing the bells.
Learn more about permutations here:
https://brainly.com/question/1216161
#SPJ4
Determine whether A and B are inverse matrices.

Answers
The matrices A and B are not inverse matrices
How to determine if the matrices are inverse matrices?From the question, we have the following parameters that can be used in our computation:
\(A = \left[\begin{array}{cc}-2&-3&2&-2\end{array}\right]\)
\(B = \left[\begin{array}{cc}1&-1&-1&2\end{array}\right]\)
To determine if the matrices are inverse matrices, we simply calculate the inverse of matrix A and then make the comparison.
The matrix A is given as
\(A = \left[\begin{array}{cc}-2&-3&2&-2\end{array}\right]\)
Calculate the determinant of the matrix A
So, we have the following representation
|A| = -2 * -2 + 3 * 2
Evaluate the sum of products
|A| = 10
The inverse is then calculated as
\(A^{-1} = \frac 1{10} * \left[\begin{array}{cc}-2&3&-2&-2\end{array}\right]\)
Evaluate
\(A^{-1} = \left[\begin{array}{cc}-\frac 1{5}&\frac 3{10}&-\frac 1{5}&-\frac 1{5}\end{array}\right]\)
When compared to matrix B, both matrices are different
Hence, the matrices are not inverse matrices
Read more about matrices at
https://brainly.com/question/11989522
#SPJ1
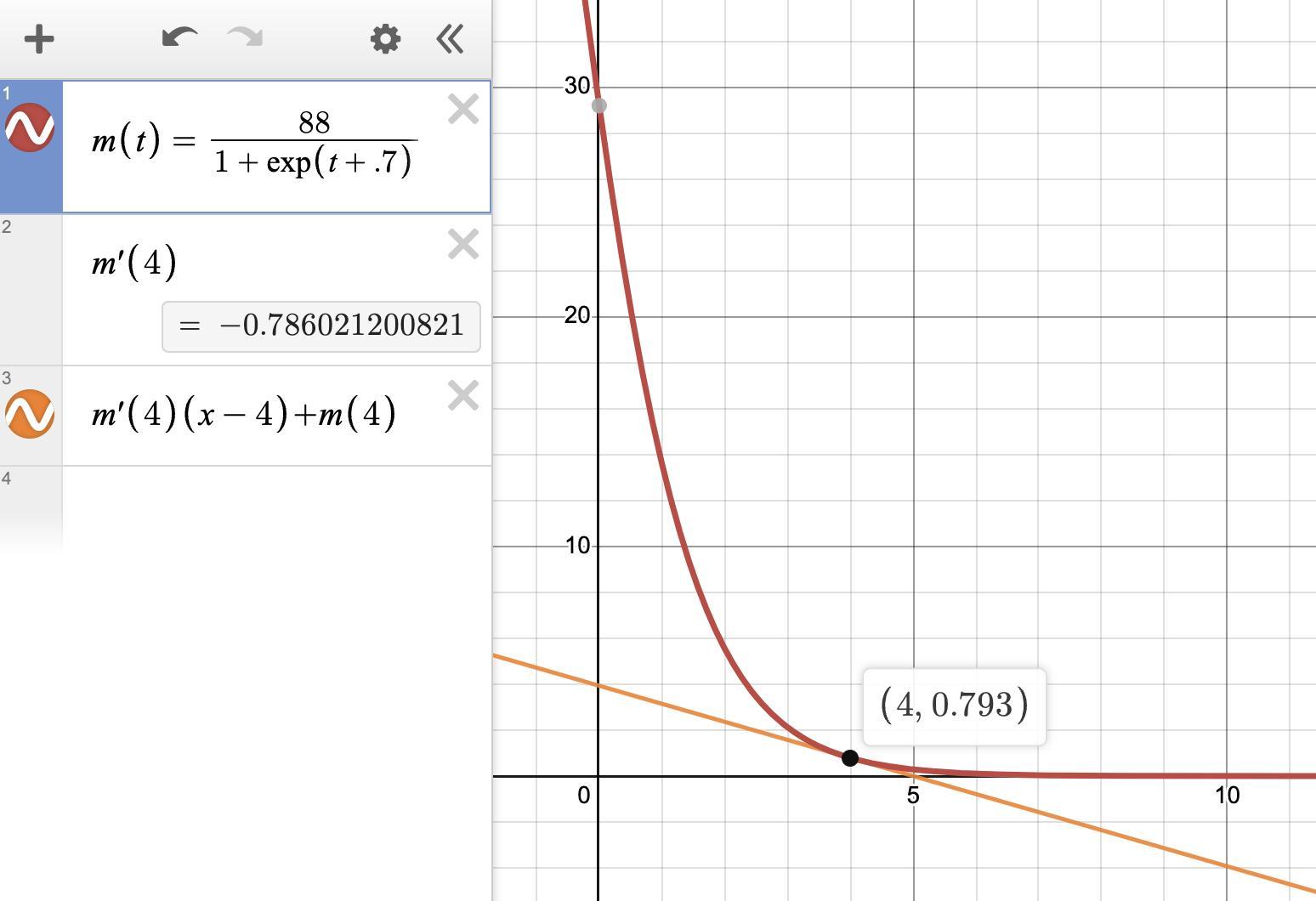
the amount of medication, in milligrams, in a patient's bloodstream after t hours, can be represented by the following function: m of t equals 88 over the quantity 1 plus e to the x plus 7 tenths power end quantity what is the rate of change for the amount of medication in the patient's bloodstream after 4 hours?
Answers
Answer:
about -0.79 mg/hour
Step-by-step explanation:
You want the rate of change of the amount of medication in a patient after 4 hours if the amount after t hours is modeled by y=88/(1+e^(t+0.7)).
Rate of changeThe rate of change is found by taking the derivative of the function with respect to time. Let u = 1+e^(t+0.7). Then du/dt = e^(t +0.7).
The function can be written ...
y = 88/u = 88·u^-1
so its derivative is ...
dy/dt = (-88·u^-2)·du/dt
dy/dt = -88(e^(t +0.7))/(1 +e^(t +0.7))^2
At t=4The value of the rate of change at t=4 is ...
dy/dt = -88(e^(4 +0.7))/(1 +e^(4 +0.7))^2 ≈ -88(109.95)/(1 +109.95)^2
dy/dt ≈ -0.78602 ≈ -0.79 . . . . . . mg/h
The rate of change in the amount of medication is about -0.79 mg/h.

On June 1, Year 1, Decker verbally guaranteed the payment of a $5,000 promissory note, which Decker's cousin owed Baker. On June 3, Year 1, Baker wrote Decker confirming Decker's guarantee. Decker did not object to the confirmation. On August 23, Year 1, Decker's cousin defaulted on the promissory note. Which of the following statements is true? a. Decker is not liable under the verbal agreement if it expired more than 1 year after June 1. b. Decker is not liable under the verbal agreement because Decker's promise was not in writing, Oc Decker is liable under the verbal guarantee because Decker did not object to Baker's June 3 letter. O d. Decker is liable under the verbal agreement because Baker demanded payment within 1 year of the date the guarantee was given
Answers
The correct statement is d. Decker is liable under the verbal agreement because Baker demanded payment within 1 year of the date the guarantee was given.
In this scenario, Decker verbally guaranteed the payment of a $5,000 promissory note owed by Decker's cousin to Baker on June 1, Year 1. On June 3, Year 1, Baker wrote a letter confirming Decker's guarantee, and Decker did not object to the confirmation. Therefore, there is a valid contract between Decker and Baker, even though the guarantee was not in writing.
On August 23, Year 1, Decker's cousin defaulted on the promissory note, and Baker demanded payment from Decker. Under the Statute of Frauds, certain contracts must be in writing to be enforceable. However, this rule does not apply to contracts for guarantees or suretyship, as long as the main obligation being guaranteed is not within the Statute of Frauds. In this case, the main obligation is the promissory note, which is not within the Statute of Frauds.
Moreover, Decker's guarantee was confirmed in writing by Baker's letter on June 3, Year 1, and Decker did not object to it. Therefore, Decker is liable under the verbal agreement. Additionally, Baker demanded payment within 1 year of the date the guarantee was given, which is within the statute of limitations for contract claims.
To know more about payment visit:-
https://brainly.com/question/30884652
#SPJ11
PLZ HELP, GIVING BRAINLIEST!! Look at the pic below to answer the question.

Answers
Answer:
D
Step-by-step explanation:
The square root of x in radical form is \(\sqrt{x}\)
In exponent form the square root of x is \(x^{\frac{1}{2} }\)
Answer:
D
Step-by-step explanation:
When you put x to a fraction for example x to the 1/2 power is the same thing as the square root of x, another example is x to 1/3 power this is the same thing as the cube root of x
Therefore x to the 1/2 power is the square root of x
Next a way to wright the square root of x is \(\sqrt{x}\)
This means that the answer is D
FIND THE VOLUME OF EACH FIGURE THANK UUU

Answers
Answer:
32
Step-by-step explanation:
Evaluate the following expression

Answers
The correct answer is 6
Answer:
6
Step-by-step explanation:
Order of Operations: BPEMDAS
Step 1: Write out expression
[9 × (10 - 2)] ÷ [2 + (5 × 2)]
Step 2: Bracket Parenthesis
[9 × 8] ÷ [2 + 10]
Step 3: Brackets
72 ÷ 12
Step 4: Divide
6
Simplify g³ x g³‼️‼️‼️
Answers
Answer:
\(g^6\)
Step-by-step explanation:
When multiplying exponents, for example
\(x^2 * x^5\)
Their power values are added together to get
\(x^2 * x^5 = x * x * x* x* x* x* x = x^7\)
Answer:
\(g^6\)
Step-by-step explanation:
because, \(g^3*g^3\) is basically \(g^(^3^+^3^)\) which is \(g^(^6^)\) = \(g^6\)
let be the tangent plane to the graph of (,)=26−132−262 at the point (4,2,−286). let (,)=26−2−2. find the point on the graph of where the tangent plane is parallel to .
Answers
The point on the graph where the tangent plane is parallel is (52, 52, -5382).
What is the tangent plane?
The surface that contains all tangent lines of the curve at a point, $P$, that lies on the surface and passes through the point is represented by the tangent plane. We discovered earlier in our talks of derivatives and tangent lines that we can use tangent lines to mimic the behavior of a graph. We may employ tangent planes for a similar reason now that we're working with multivariable functions and three-dimensional coordinate systems.
Here, we have
Given: Let P be the tangent plane to the graph of g(x, y) = 26 – 13x² – 26y² at the point (4, 2, –286). Let f(x, y) = 26 – x² - y².
We have to find the point on the graph where the tangent plane is parallel.
Let P be the tangent plane to the graph z = g(x, y) = 26 – 13x² – 26y² at the point (4, 2, –286).
φ(x,y,z) = 13x² + 26y² + z - 26
Δφ = 26xi + 52yj + k
Δφ(4, 2, –286) = 104i + 104j + k
Then,
P: 104(x-4) + 104(y-2)+1(z+286) = 0
104x + 104y + z = 338...(1)
Now, Let
ψ(x,y,z) = x² + y² + z - 26
Δψ = 2xi + 2yj + k
Let (x₀,y₀,z₀) be the point of the graph z = f(x,y) = 26 – x² - y² where the tangent plane in the plane is parallel to equation (1).
Δψ (x₀,y₀,z₀) = (2x₀,2y₀,1)
= 2x₀/104 = 2y₀/104 = 1/1
x₀ = 52 = y₀
Now, z₀ = 26 – x₀² - y₀² = 26 – 52² - 52²= -5382
Hence, the point on the graph where the tangent plane is parallel is (52, 52, -5382).
To learn more about the tangent plane from the given link
https://brainly.com/question/30452856
#SPJ4
the length of human pregnancies from conception to birth is, on average, 266 days with a standard deviation of 16 days. suppose a random sample of 25
Answers
The student question is asking about the average length of human pregnancies and the standard deviation based on a random sample of 25 pregnancies. This means that the actual average length of pregnancies for this sample could vary within 3.2 days above or below the given mean of 266 days.
To answer this question, first, we'll restate the provided information:
- The average length of human pregnancies is 266 days.
- The standard deviation is 16 days.
- We have a random sample of 25 pregnancies.
Now, we'll use this information to find the mean and standard error for the sample.
Step 1: Calculate the mean of the sample.
The mean of the sample is the same as the population mean, which is 266 days.
Step 2: Calculate the standard error.
Standard error (SE) is calculated using the following formula:
SE = (standard deviation) / sqrt(sample size)
In this case:
SE = 16 / sqrt(25)
SE = 16 / 5
SE = 3.2 days
So, the standard error for the sample is 3.2 days.
In conclusion, based on the random sample of 25 pregnancies, the average length of human pregnancies is 266 days with a standard error of 3.2 days.
For more questions on standard deviation
https://brainly.com/question/475676
#SPJ11
Leo Gandolfi takes out a short-term loan of $1,800 at 12 percent
for 6 months. The monthly payment is $310.50. The balance of the loan after 4 payments is
$612.34. How much does he save by paying off the loan when the next payment is due?
A $6.12
R2 $18.00
C
2,353
SCIO
Answers
In a linear equation, 9.14 does he save by paying off the loan when the next payment is due .
What in mathematics is a linear equation?
An algebraic equation with simply a constant and a first-order (linear) term, such as y=mx+b, where m is the slope and b is the y-intercept, is known as a linear equation.
Sometimes, the aforementioned is referred to as a "linear equation of two variables," where x and y are the variables.
Jan 293 18 311 1,507 16.25%
Feb 296 15 311 1,212 32.67%
Mar 298 12 311 913 49.25%
Apr 301 9 311 612 66.00%
May 304 6 311 308 82.92%
Jun 308 3 311 0 100.00%
Learn more about a linear equation
brainly.com/question/29739212
#SPJ1
a1 =4 and an=-1+1 then find the value of a5
Answers
The value of a5 is 8.
Given that,
a₁ = 4
aₙ = aₙ₋₁ + 1
So, we can find the second term a₂ using the equation of nth term,
a₂ = a₍₂₋₁₎ + 1
a₂ = a₁ + 1
Applying the value of a₁,
a₂ = 4 + 1
a₂ = 5
So, finding the value of a₃,
a₃ = a₍₃₋₁₎ + 1
a₃ = a₂ + 1
a₃ = 5 + 1
a₃ = 6
So, the value of a₄ will be,
a₄ = a₃ + 1 = 6 + 1
a₄ = 7
Therefore,
a₅ = a₄ + 1 = 7 + 1
a₅ = 8
To learn more about arithmetic sequence, click:
https://brainly.com/question/15412619
#SPJ1
let g and h be the functions defined by g(x)=sin(π2(x 2)) 3 and h(x)=−14x3−32x2−94x 3. if f is a function that satisfies g(x)≤ f(x) ≤ h(x) for −2
a. 3
b. 3,5
c. 4
d. The limit cannot be determined from the information given
Answers
The limit of the given function is (c) 4.
To determine the limit, we need to find the value of f(x) as x approaches 2. From the given inequality, we know that g(x) is the lower bound of f(x), while h(x) is the upper bound.
Let's first evaluate g(2):
g(2) = sin(π/2 * (2^2)) ^3 = sin(2π) ^3 = 0
Now let's evaluate h(2):
h(2) = -(1/4)(2^3) - (3/2)(2^2) - (9/4)(2) = -5
Since f(x) is bounded between g(x) and h(x), we know that the limit of f(x) as x approaches 2 must be between 0 and -5. Therefore, the only possible answer is (c) 4, which lies between 0 and -5. However, we cannot determine the exact value of the limit from the given information.
For more questions like Function click the link below:
https://brainly.com/question/16008229
#SPJ11
The regular price of a camera is 180.00 the camera is on sale for 25% off the regular price. What is the sales price of the camera in dollars and cents
Answers
Answer:
$135
Step-by-step explanation:
180 decrease 25% =
180 × (1 - 25%) = 180 × (1 - 0.25) = 135
CAN u pls pls pls help its easy for yall not me im slow

Answers
Answer:
A
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
2.25/.5
28 days = ? Weeks 339 days = ? Months 14 months = ? Days 8 weeks = ? Days 90 days = ? Months 3 minutes = ? Seconds 3days = ? Hours 48 days = ? Days 5 minutes = ? Seconds
Answers
Answer:
28 days = 4 weeks
339 days = 11 month
14 months = 420 days
8 weeks = 56 days
90 days = 3 months
3 minutes = 90 seconds
3 days = 72 hours
48 days = 48 days
5 minutes = 300 seconds
Find an equation of the ellipse with foci (3,2) and (3,-2) and
major axis of length 8
Answers
The equation of the ellipse is \((x - 3)^2 / 16 = 1\)
How to o find the equation of the ellipse?To find the equation of the ellipse with the given foci and major axis length, we need to determine the center and the lengths of the semi-major and semi-minor axes.
Given:
Foci: (3, 2) and (3, -2)
Major axis length: 8
The center of the ellipse is the midpoint between the foci. Since the x-coordinate of both foci is the same (3), the x-coordinate of the center will also be 3. To find the y-coordinate of the center, we take the average of the y-coordinates of the foci:
Center: (3, (2 + (-2))/2) = (3, 0)
The distance from the center to each focus is the semi-major axis length (a). Since the major axis length is 8, the semi-major axis length is a = 8/2 = 4.
The distance between each focus and the center is also related to the distance between the center and each vertex (the endpoints of the major axis). This distance is the semi-minor axis length (b).
The distance between the foci is given by 2c, where c is the distance from the center to each focus. In this case, 2c = 2(2) = 4. Since the center is at (3, 0), the vertices are located at (3 ± a, 0). Therefore, the distance between each focus and the center is b = 4 - 4 = 0.
We now have the center (h, k) = (3, 0), the semi-major axis length a = 4, and the semi-minor axis length b = 0.
The equation of an ellipse with its center at (h, k) is given by:
\(((x - h)^2 / a^2) + ((y - k)^2 / b^2)\) = 1
Substituting the values, we have:
\(((x - 3)^2 / 4^2) + ((y - 0)^2 / 0^2)\) = 1
Simplifying the equation, we get:
\((x - 3)^2 / 16 + 0 = 1\)
Therefore, the equation of the ellipse is:
\((x - 3)^2 / 16 = 1\)
To know more about ellipse , refer here:
https://brainly.com/question/20393030
#SPJ4
You buy 1.65 pounds of apples and 1.85 pounds of plums. Apples and plums sell for the same price per pound. The total cost, after using a 65cents-off coupon, is $3.20. If c represents the cost of the fruit in dollars per pound, what equation could you use to find the value of c?
Answers
Answer:the value is 20
Step-by-step explanation:
Please help
will put brainliest to who answers in the next 10 - 20 minutes

Answers
3) See this number pattern carefully. Every row of numbers has a certain
relation with the numbers in the row just above it.
What number should replace ‘x’?
a) 7.5
b) 5
c) 4
d) 3

Answers
Answer:
x = 5Step-by-step explanation:
the sum of the hexes above results in the hex below
x + 2x = 15
3x = 15
x = 15 . 3
x = 5
----------
check
x + 2x = 15
5 + 2* 5 =
5 + 10 =
15
The answer is good
find the centroid of the region in the first quadrant bounded by the given curves. y = x8, x = y8
Answers
The centroid of the region in the first quadrant bounded by the given curves is (81/170, 81/170).
In the given question, we have to find the centroid of the region in the first quadrant bounded by the given curves.
The given curves are:
y = x^8, x = y^8
We can write the curves as
y = x^8...........................(1)
y = x^{1/8}.......................(2)
Now putting the value of y from equation 1 in equation 2, we get
x^8 = x^{1/8}
Now simplifying,
x^{64} = x
x^{64}-x = 0
x(x^{63} - 1) = 0
After equating equal to zero,
x = 0, x = 1
My = \(\int_{a\rightarrow b}x[f(x)-g(x)]dx\)
My = \(\int_{0}^{1}x[x^{1/8} - x^{8}]dx\)
My = \(\int_{0}^{1}[x^{9/8} - x^{9}]dx\)
My = \([(8/17)x^{17/8} - (1/10)x^{10}]_{0}^{1}\)
My = (8/17)-(1/10)
My = 63/170
Mx = 1/2\(\int_{a\rightarrow b}[(f(x))^2-(g(x))^2]dx\)
Mx = 1/2\(\int^{1}_{0}[x^{1/4} - x^{16}]dx\)
Mx = 1/2 \([(4/5)x^{5/4} - (1/17)x^{17}]^{1}_{0}\)
Mx = (1/2)[(4/5)- (1/17)]
Mx = 63/170
M = \(\int_{a\rightarrow b}[f(x)-g(x)]dx\)
M = \(\int^{1}_{0}[x^{1/8} - x^{8}] dx\)
M = \([(8/9)x^{9/8} - (1/9)x^{9}]^{1}_{0}\)
M = [(8/9) - (1/9)]
M =7/9
Center of mass(x',y') = (My/M, Mx/M)
Center of mass(x',y') = ((63/170)/(7/9), (63/170)/(7/9))
Center of mass(x',y') = (81/170, 81/170)
To learn more about Center of mass link is here
brainly.com/question/23160538
#SPJ4