Answers
Answer:
The answer to the problem is Leah had the shortest distance.
Step-by-step explanation:
Okay to solve this problem we must covert the fractions into decimals
(Maria) 5/6 as a decimal = 0.83
(Leah) 2/3 as a decimal = 0.66
(Jonas) 3/4 as a decimal 0.75
So who had the shortest distance??? Leah had the shortest distance.
Hope that helps. Please mark me brainliest I would appreciate it.
Related Questions
Help me solve this and if you could explain it would be great

Answers
Answer: the equation is 3x=12
Step-by-step explanation:
The coefficient is 3 because the coefficient is the number being multiplied by the variable (x).
To find the solution you have to divide both sides of the equation by 3 to find what times 3 will give you 12. After dividing both sides by 3 you get this equation. X=4
So this means that the solution is 4.
Hope this helps :)
The function g is defined by g(x) = 3x+4.
Find g(z+3).
I really need help with these Aleks assignments, can someone help me with them?
Answers
Answer:g(x) = (x+3)/(x2-4)
The domain refers to all of the x values that the function can take on. In a rational expression like the one above, we have to be careful that the denominator is never 0, since division by 0 is undefined. We can factor the denominator of g(x) as follows:
g(x) = (x+3)/((x+2)(x-2)
The denominator will be zero when x = 2 or -2. Otherwise, g(x) is defined on all other values of x. So the domain of g(x) is "x = all x not equal to -2 or 2". In interval notation, the domain is:
(-∞,-2)U(-2,2)U(2,+∞)
On a number line, draw it as follows:
-∞ <======o=====o=======> +∞
-2 2
Step-by-step explanation:
Please help me thanks

Answers
Answer: Choice B
Step-by-step explanation:
The formula for the area of a circle is πr², and the radius is 1/2 of the diameter.
In the circle shown, the diameter is 18 m. Since the radius is half the diameter, the circle's radius is 9 m.
Inputting this value into this equation gives us π·9², or 81π. Putting this into a calculator or solving it with an approximation of pi gives us a number close to 254.46 m².
The closest option to that is B, so that is your answer.
Does anyone know how much does a Toyota AE86 car gets for monthly car payments??
not math-related sorry
Answers
Answer:
$464
Step-by-step explanation:
When a number is increased by 9.5%, the result is 58. What is the original number to the nearest tenth?
(I've seen other questions like this, but the answer is wrong. It's not 50 or 52.49 or 52.5.)
Answers
Answer:
53
Step-by-step explanation:
58÷1.095= 53 is the answer
Answer:
5.03196347032
Step-by-step explanation:
We do:
.095x+x=58
1.095x=58
x=52.96
52.96 is a approximation and when you do the math and see what 9.5 of 52.96 plus 52.96 is you get 57.9912 which is super close to 8 The exact answer is x = 5.03196347032
On the map, 0.1 inches represents
25 miles. If the real distance between
two cities is 112.5 miles, what is the
distance between their locations on
the map?
A. 0.45 in
B. 2 in
C. 0.2 in
D. 1 in
Answers
The distance between the two cities on the map is 0.45 inches , the correct option is (A) 0.45inches .
In the question ,
it is given that
the scale factor of the map is 25 miles = 0.1 inches
So, 1 mile = 0.1/25 inches
= 0.004 inches
So , on the map 1 mile is represented by 0.004 inches
Given that the real distance between the two cities is 112.5 miles
So , on the map 112.5 miles = 112.5*0.004 inches
= 0.45 inches
Therefore , the distance between the two cities on the map is 0.45 inches , the correct option is (A)0.45inches .
Learn more about Scale Factor here
https://brainly.com/question/4526389
#SPJ1
please help me with this

Answers
Measure of angle I greater than angle K and J. Therefore, option D is the correct answer.
Given that, in triangle IJK, JK=18, KI=11, and IJ=14.
What is the triangle inequality theorem?If one side of a triangle is longer than another side, then the angle opposite the longer side will be larger than the angle opposite the shorter side.
Here, JK is the longest side and KI is the shortest side
So, opposite to side JK, angle I is the biggest and opposite to the side KI angle J is the smallest
Here, the measure of IJ is greater than the side KI, then the angle K opposite to side IJ is greater than the angle J
Thus, m∠I>m∠K>m∠J
Measure of angle I greater than angle K and J. Therefore, option D is the correct answer.
To learn more about the triangle inequality theorem visit:
https://brainly.com/question/1163433.
#SPJ1
Find the slope of the line that passed through (5,8) and (1,13)
Answers
Answer:
Slope is -5/4
Step-by-step explanation:
to find the slope of two points, you subtract the y values/x values. So 8-13/5-1 which ends up as -5/4 which is the answer.
please help me
"Use the graph to write a linear function that relates y to x."

Answers
Answer:
y = -4x-2
Step-by-step explanation:
from the graph
four $12$-sided dice are rolled. what is the probability that the number of dice showing a two digit number is equal to the number of dice showing a one digit number? express your answer as a common fraction. (assume that the numbers on the $12$ sides are the numbers from $1$ to $12$ expressed in decimal.)
Answers
27/128 is the probability that the number of dice showing a two-digit number is equal to the number of dice showing a one-digit number.
Probability means Possibility. It states how likely an event is about to happen.
The probability of an event can exist only between 0 and 1 where 0 indicates that the event is not going to happen i.e. Impossibility and 1 indicates that it is going to happen for sure i.e. Certainty.
I'll take a stab at this one. if the number of dice showing a two-digit number = the number of dice showing a one-digit number, then 2 must show a two-digit number and 2 must show a one-digit number
There are 3 two-digit numbers and 9 one-digit numbers on each die
So....the probability is
C(4,2) (3/12)^2 (9/12)^2
C(4,2) (1/4)^2 (3/4)^2
=27/128.
To learn more about probability:
https://brainly.com/question/28019908
#SPJ4
f(x) = (x-2)(x+1)
————-
x+1
Which statements describe the end behavior of the graph of the function shown? Check all that apply.
• As x to infinity, y to 1.
•As x to infinity, y to infinity
•As x to infinity, y to negative infinity
•As x to negative infinity, y to - 1
•As x to negative infinity, y to infinity
•As x to negative infinity, y to negative infinity
Answers
Answer:
As x to negative infinity, y to negative infinity
Step-by-step explanation:
Project Profit (in million $) Investment (in million $)1 0.50 22 1.40 53 1.70 124 1.10 25 4.00 156 0.60 37 2.50 108 1.10 1BeFair wants to decide which projects to fund so that the total profit will be maximized. Formulate this problem in the space provided on the answer sheet.
Answers
The total profit will be maximized by using the objective function Z = 22x₁ + 53x₂ + 124x₃ + 25x₄ + 156x₅ + 37x₆ + 108x₇ + x₈
To formulate this problem mathematically, we need to define the decision variables, objective function, and constraints.
We will define a binary decision variable, \(x_i\), which indicates whether or not to invest in project i. If \(x_i\) = 1, the project i will be funded, and if \(x_i\) = 0, the project i will not be funded.
The objective is to maximize the total profit earned by investing in the selected projects. Thus, the objective function can be written as:
Maximize Z = 22x₁ + 53x₂ + 124x₃ + 25x₄ + 156x₅ + 37x₆ + 108x₇ + x₈
This objective function adds the profit of all the projects that will be funded based on the decision variable \(x_i\).
The total investment cannot exceed the available investment budget of $1 million, which can be written as:
0.50x₁ + 1.40x₂ + 1.70x₃ + 1.10x₄ + 4.00x₅ + 0.60x₆ + 2.50x₇ + 1.10x₈ <= 1
Additionally, the decision variables are binary, which means that x_i can only be either 0 or 1. Therefore, we can add binary constraints for each decision variable as follows:
x_i = 0 or 1 for i = 1,2,3,4,5,6,7,8
To know more about profit here
https://brainly.com/question/15522421
#SPJ4
Rachana has a set of ten mugs the set up is made of 3 different mugs
Answers
If Rachana randomly selects two mugs from the set, the probability that she gets two different mugs is 0.1556 or 15.56%.
To solve this problem, we can use the concept of combinations. Since there are 10 mugs in the set, there are 10 choose 2 = 45 ways to select two mugs without considering order.
Out of these 45 ways, we need to count the number of ways Rachana can select two different mugs. Since there are 3 different types of mugs, Rachana can choose any one of the three types for the first mug. There are 10 mugs in the set, out of which 3 belong to the chosen type. Therefore, the probability of choosing a mug of the chosen type is 3/10.
For the second mug, Rachana can choose from the remaining 9 mugs. Since she needs to choose a different type of mug, she can choose any one of the 2 remaining types. There are 7 mugs left from the other 2 types. Therefore, the probability of choosing a mug of a different type is (7/9) * 2/3 = 14/27.
Therefore, the probability of selecting two different mugs is the product of the probabilities of selecting a mug of the chosen type and a mug of a different type. This is given by (3/10) * (14/27) = 7/45, which is approximately 0.1556 or 15.56%.
To learn more about probability click on,
https://brainly.com/question/25905476
#SPJ4
Complete question is:
Rachana has a set of ten mugs the set up is made of 3 different mugs. If Rachana randomly selects two mugs from the set, what is the probability that she gets two different mugs?
Q4) Given three vectors A = - ax + 2ay +3az and B = 30x + 4ay + 5z and C=2ax - 2ay +7az. Compute: a. The scalar product A.B b. The angle between A and B. c. The scalar projection of A on B.
Answers
To compute the given quantities, let's use the properties of vector operations:
a. The scalar product (dot product) of two vectors A and B is given by the formula:
A · B = |A| |B| cos(∅),
where |A| and |B| are the magnitudes of vectors A and B, and ∅ is the angle between them.
Calculating the scalar product:
A · B = (-a)(30) + (2)(4) + (3)(5) = -30a + 8 + 15 = -30a + 23.
b. The angle between two vectors A and B can be found using the formula:
cos(∅) = (A · B) / (|A| |B|),
where ∅ is the angle between A and B.
Calculating the angle:
cos(∅) = (-30a + 23) / √((\(a^2\) + 4 + 9)√(900 + 16 + 25))
∅= acos((-30a + 23) / √((\(a^2\) + 13)(941)))
c. The scalar projection of vector A onto vector B is given by the formula:
scalar projection of A onto B = |A| cos(∅),
where ∅ is the angle between A and B.
Calculating the scalar projection:
scalar projection of A onto B = √(\(a^2\) + 4 + 9) cos(∅)
Learn more about scalar product here:
https://brainly.com/question/30176252
#SPJ11
Each unit of food A contains 120 milligrams of sodium, 1 gram of fat, and 5 grams of protein. Each unit of food B contains 60 milligrams of sodium, 1 gram of fat, and 4 grams of protein. Suppose that a meal consisting of these two types of food is required to have at most 480 milligrams of sodium and at most 6 grams of fat. Find the combination of these two foods that meets the requirements and has the greatest amount of protein. 1) Define your variables. 2) Create an organizational chart of information. 3) Create an objective equation (what is to be maximized or minimized). 4) Write constraint inequalities. Don't forget the non-negative restrictions if applicable. 5) Graph the constraints in order to identify the feasible region. 6) Find the vertices of the feasible region. 7) Test all vertices in the objective equation to identify the point of optimization. 8) Write the complete solution with clear and concise language.
Answers
The combination of food A and food B that meets the requirements and has the greatest amount of protein is 2 units of food A and 1 unit of food B, with a total of 30 grams of protein.
We can approach the problem of finding the combination of food A and food B that meets the requirements and has the greatest amount of protein using linear programming.
1) Variables:
Let x be the number of units of food A.
Let y be the number of units of food B.
2) Organizational chart:
Food A:
Sodium: 120 mg/unit
Fat: 1 g/unit
Protein: 5 g/unit
Food B:
Sodium: 60 mg/unit
Fat: 1 g/unit
Protein: 4 g/unit
Meal requirements:
Sodium: ≤ 480 mg
Fat: ≤ 6 g
Objective: Maximize protein
3) Objective equation:
Maximize z = 5x + 4y
4) Constraint inequalities:
120x + 60y ≤ 480 (sodium constraint)
x + y ≤ 6 (fat constraint)
x ≥ 0, y ≥ 0 (non-negative constraint)
5) Graph the constraints:
To graph the constraints, we can first graph the boundary lines.
120x + 60y = 480
x + y = 6
Then we can shade the feasible region, which is the region that satisfies all the constraints.
The feasible region is a polygon with vertices at (0,0), (4,2), (6,0), and (3,3).
6) Find the vertices:
The vertices of the feasible region are (0,0), (4,2), (6,0), and (3,3).
7) Test the vertices:
We can test each vertex by substituting its coordinates into the objective equation and finding the maximum value.
(0,0): z = 0
(4,2): z = 30
(6,0): z = 30
(3,3): z = 27
The maximum value of the objective function is 30, which occurs at the points (4,2) and (6,0).
8) Write the complete solution:
To maximize protein while satisfying the sodium and fat constraints, we need to use 4 units of food A and 2 units of food B, or 6 units of food A and 0 units of food B. Both of these combinations have a total of 30 grams of protein.
Know more about protein here:
https://brainly.com/question/29776206
#SPJ11
Increased by 75% is 35 ?
Answers
Answer:
20
Step-by-step explanation:
20 + (75% × 20) =
20 + 75% × 20 =
(1 + 75%) × 20 =
(100% + 75%) × 20 =
175% × 20 =
175 ÷ 100 × 20 =
175 × 20 ÷ 100 =
3,500 ÷ 100 =
35;
ii.) 2 ( x + 3 ) = 15
Answers
Answer:
2(x+3)=15
2x+6=15
2x=9
x= 4.5
Step-by-step explanation:
please pass this on... ( #helpsavelives )
Who ever is reading this:
I love u.
U matter.
The world needs u
hang in there ik it may be bad but u deserve the world <3
ur beautiful no matter ur shape, size, color, gender.. anything
don't give up i need u to live.
i wish i could take everyones problems so yall wouldn't have to have em but i cant so just know ily and if anyone needs to talk u can talk to me
Pls pass this on. Everyone deserves to know this. ♥️♥️
just copy and paste its not hard pls this could save someones life
What is the part of line having 1 endpoint and extending in one direction?
Answers
A part of a line that has 1 endpoint and extends indefinitely in only one direction is called a ray.
A ray is named using its endpoint first, and then any other point on the ray
Properties of ray:
A line is a series of points placed together that continue infinitely.When this line is restricted from one direction and is extended in the other direction indefinitely, it forms a ray.It has just one starting point and does not have an opposite end and goes through and cuts many points and lines and is often used to draw angles, and we cannot measure the length of a ray.To know more about ray:
https://brainly.com/question/28045419
#SPJ4
A clay specimen, 25 mm thick, has been tested in an oedometer apparatus with two way rainage, and it is observed that 50% of the consolidation settlement occurs in 1 hour. A ayer of the same clay is observed to settle 10 mm in 10 years and after many years to settle (total primary consolidation) by 35 mm. Determine the thickness of the clay layer if it drains only from upper surface
Answers
The thickness of the clay layer, which drains only from the upper surface, can be determined based on the consolidation settlement observations. With 50% of consolidation settlement occurring in 1 hour for a 25 mm thick specimen, and a total primary consolidation settlement of 35 mm occurring over many years, the thickness of the clay layer is approximately 87.5 mm.
The consolidation settlement of a clay specimen can be used to estimate the thickness of a clay layer that drains only from the upper surface. In this case, the observed settlement data provides valuable information.
Firstly, we know that 50% of the consolidation settlement occurs in 1 hour for a 25 mm thick clay specimen. This is an important parameter for calculating the coefficient of consolidation (Cv) using Terzaghi's theory. From the Cv value, we can estimate the time required for full consolidation settlement.
Secondly, we are given that the same clay settles 10 mm over 10 years and eventually settles a total of 35 mm over a longer period. This long-term settlement is known as the total primary consolidation settlement. By comparing this settlement value with the settlement data from the oedometer test, we can determine the thickness of the clay layer.
To calculate the thickness, we can use the concept of the consolidation settlement ratio. The ratio of the total primary consolidation settlement to the consolidation settlement at 50% completion is equal to the ratio of the total thickness to the thickness at 50% completion. Applying this ratio, we can determine that the thickness of the clay layer, which drains only from the upper surface, is approximately 87.5 mm.
To learn more about thickness click here: brainly.com/question/23622259
#SPJ11
Add/Subtract the following polynomials.
1. (3x^2– 5x) + (-x^2- 7X +5)
Answers
hope this helps<3
Use the given graph to complete the table. Then write an equation representing the relationship.
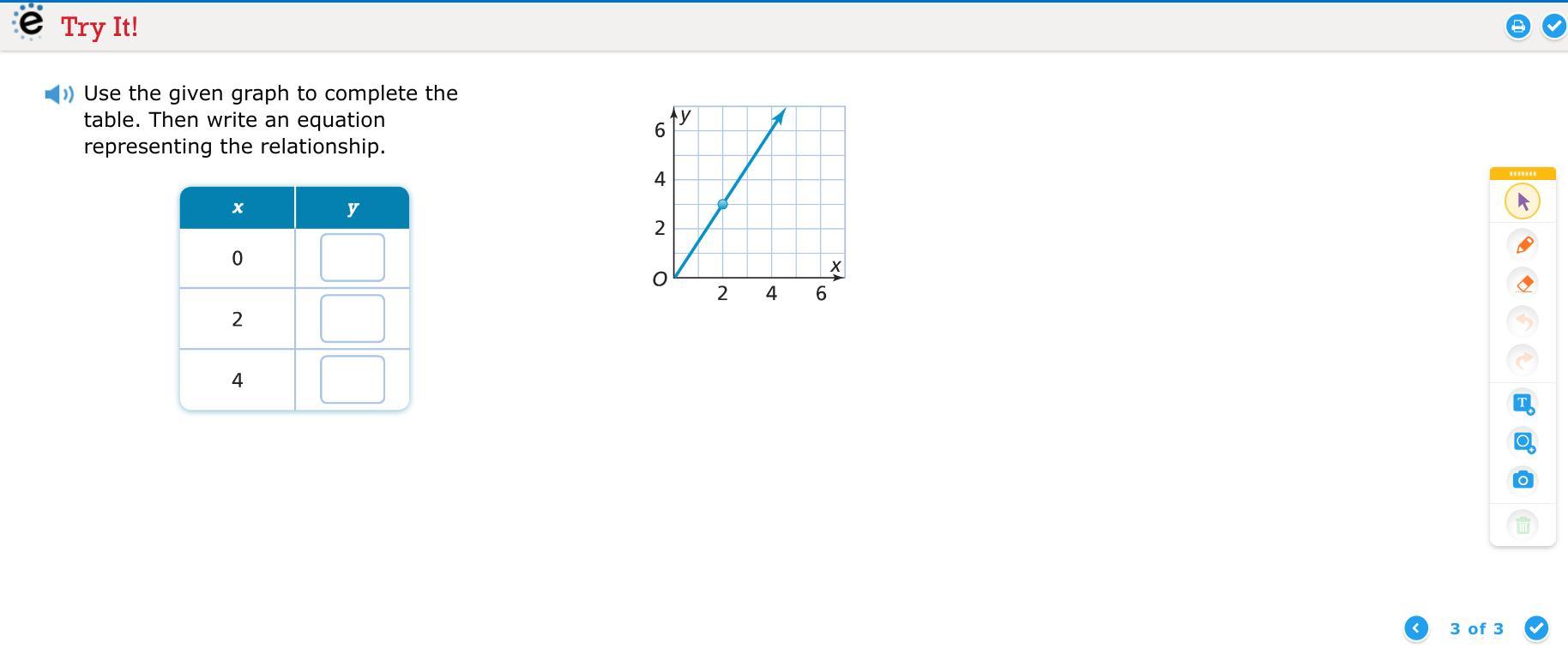
Answers
The equation of the relation is y = 3/2x.
x | y
0 0
2 3
4 6
How to Write the Equation that Represents a Proportional Relationship?To write the equation for the proportional relationship between two variables, x and y, find the unit rate, k, which is k = y/x.
Substitute the value of k into y = kx to write the equation of the relationship.
Using a point on the line, (2, 3):
k = y/x = 3/2
Substitute k = 3/2 into y = kx:
y = 3/2x
Using the equation, substitute each of the values of x in the table to get the corresponding value of y:
For 0:
y = 3/2(0)
y = o
For 2:
y = 3/2(2)
y = 3
For 4:
y = 3/2(4)
y = 6
The table is:
x | y
0 0
2 3
4 6
Learn more about equation of relationship on:
https://brainly.com/question/6869319
#SPJ1
Helppppppp meee plsss

Answers
Answer:
C
Step-by-step explanation:
an 11 foot ladder is placed against the wall. the ladder is on ground level at an angle of 73.5° to the horizontal. about how far up the wall will the top of the ladder be
Answers
The 10.547 feet up the wall will the top of the ladder be if the 11-foot ladder is placed against the wall. The ladder is on ground level at an angle of 73.5° to the horizontal.
What is trigonometry?Trigonometry is a branch of mathematics that deals with the relationship between sides and angles of a right-angle triangle.
Length of the ladder = 11 foot
The angle between ladder and horizontal = 73.5 degree
The height of the wall, the top of the ladder be(h):
From the sin ratio:
sin73.5 = h/11
h = 11sin73.5 = 10.547 feet
Thus, the 10.547 feet up the wall will the top of the ladder be if the 11-foot ladder is placed against the wall. The ladder is on ground level at an angle of 73.5° to the horizontal.
Learn more about trigonometry here:
brainly.com/question/26719838
#SPJ1

(HELP PLEASE!! answer all the questions) Mr. Smith decorates his U.S. History classroom by putting up pictures of the presidents. The wall is 9.75 feet long. In the center, there is a window that is 5 34feet long.
Each president's picture is 6 inches wide.
If the pictures are placed side by side on either side of the window, how many pictures can he fit on this wall?
Answer the questions to solve this problem.
1. How many feet long is the space Mr. Thuman wants to fill with pictures? Explain how you know.
Write your answer in the space below.
2. Convert this length to inches. (There are 12 inches in 1 foot)
Write your answer in the space below.
3. How many pictures will Mr. Thuman use? Explain how you found your answer.
Write your answer in the space below.
4. How would your answer change if the pictures were 10 inches wide? Explain.
Write your answer in the space below.

Answers
9514 1404 393
Answer:
4.00 feet48 inches8 pictures4 picturesStep-by-step explanation:
1. The available wall space is the difference between the length of the wall and the length of the window:
9.75 ft - 5.75 ft = 4.00 feet
__
2. At 12 inches per foot, this is ...
(4 ft)(12 in/ft) = 48 in
__
3. If the pictures are 6 inches wide, Mr. Smith can use ...
(48 in)/(6 in/picture) = 8 pictures
__
4. If the pictures are 10 inches wide, Mr. Smith can use ...
(48 in)/(10 in/picture) = 4.8 pictures
There is room for 4 pictures. Space for a fraction of a picture is not useful. This number is even, so 4/2 = 2 pictures can be placed on either side of the window.
Write a quadratic function h whose zeros are 10 and 3
Answers
The quadratic function is x² - 13x + 30.
What is a quadratic function?A polynomial function with one or more variables, where the largest exponent of the variable is two, is referred to as a quadratic function.
A quadratic function is one of the form:
f(x) = ax²+ bx + c,
where a, b, and c are numbers with a not equal to zero.
Let m and n be the zeros of the quadratic function.
So, the quadratic function is
f(x) = c(x-m)(x-n),
where c is the constant common term and m, n are zeros.
Simplifying,
f(x) = x² -mx - nx + mn.
Here, given zeros of the quadratic equation are 10 and 3.
That means,
if function is subjected to x.
Then (x-10) and (x-3) are factors of the quadratic function.
To write a quadratic function:
we multiply the factors,
(x-10)(x-3)
= x² -10x - 3x + 30
= x² - 13x + 30
Therefore, the quadratic function is x² - 13x + 30.
To learn more about the quadratic function;
https://brainly.com/question/29775037
#SPJ1
Two point charges of 6.73 x 10-9 C are situated in a Cartesian coordinate system. One charge is at the origin while the other is at (0.85, 0) m. What is the magnitude of the net electric field at the location (0, 0.87) m?
Answers
When calculating the electric field, we use the principle of superposition. Superposition is an idea in physics that says that when two waves pass through each other, the result is the sum of the amplitudes of the two waves. Superposition is also relevant to the addition of forces and fields, and can be used to find the net electric field produced by two charges. Therefore, the net electric field is the sum of the electric fields of the two charges. We can use Coulomb’s law to determine the electric field created by each point charge. Coulomb’s law states that the magnitude of the electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.
The equation for Coulomb’s law is F=kQ1Q2/r².
where F is the force, Q1 and Q2 are the charges of the two particles, r is the distance between the two particles, and k is Coulomb’s constant.
To find the net electric field at the location (0,0.87) m, we have to use the distance formula to find the distance between the point charge and the location.
The distance between the point charge at the origin (0,0) and the point (0,0.87) m is d = 0.87 m
The distance between the point charge at (0.85,0) and the point (0,0.87) m is d = sqrt[(0.85 m)² + (0.87 m)²] = 1.204 m
Now, we can find the electric field due to each charge and add them up to get the net electric field.
Electric field due to the point charge at the origin:
kQ/r² = (9 x 10⁹ N·m²/C²)(6.73 x 10⁻⁹ C)/(0.87 m)² = 5.99 x 10⁴ N/C
Electric field due to the point charge at (0.85,0) m:
kQ/r² = (9 x 10⁹ N·m²/C²)(6.73 x 10⁻⁹ C)/(1.204 m)² = 3.52 x 10⁴ N/C
The net electric field is the vector sum of the electric fields due to each charge.
E = E1 + E2
E = (5.99 x 10⁴ N/C)i + (3.52 x 10⁴ N/C)j
E = (5.99 x 10⁴ N/C)i + (3.52 x 10⁴ N/C)k
E = sqrt[(5.99 x 10⁴ N/C)² + (3.52 x 10⁴ N/C)²]
E = 7.02 x 10⁴ N/C
Therefore, the magnitude of the net electric field at the location (0,0.87) m is 7.02 x 10⁴ N/C.
Learn more about Cartesian coordinate system here
https://brainly.com/question/4726772
#SPJ11
Susan paints a stack of 30 blocks in a pattern. Starting from the bottom, she paints every 3rd block red and every 5th block green. Wherever red and green land on the same block, she paints that block yellow.
The 3rd block from the bottom that is painted green is how many blocks up from the bottom?
Answers
Answer:
20 blocks
Step-by-step explanation:
Help if you know thanks

Answers
x= - 1/2,-1
or
x= - 0.5, -1
Answer:
x = -1/2 x=-1
Step-by-step explanation:
2x( x+1.5) = -1
Distribute
2x^2 + 3x = -1
Add 1 to each side
2x^2 +3x+1 = 0
Factor
(2x+1) (x+1) =0
Using the zero product property
2x+1 = 0 x+1=0
2x = -1 x=-1
x = -1/2 x=-1
se polar coordinates to find the volume of the solid below the cone z=x^2 y^2 and above the ring 1 x^2y≤
Answers
The volume of the solid below the cone z = x²y² and above the ring 1 ≤ x² + y² ≤ 4 in polar coordinates is (64π/15).
To find the volume of the solid, we integrate the function representing the cone over the region defined by the ring in polar coordinates.
In polar coordinates, the cone equation z = x²y² can be expressed as z = r²cos²(θ)sin²(θ), where r represents the radial distance and θ represents the angle.
The region defined by the ring can be expressed as 1 ≤ r² ≤ 4.
To find the volume, we integrate the function z = r²cos²(θ)sin²(θ) over the region of the ring in polar coordinates.
V = ∫∫∫ r²cos²(θ)sin²(θ) r dr dθ
= ∫[0,2π] ∫[1,2] r³cos²(θ)sin²(θ) dr dθ
= ∫[0,2π] ∫[1,2] r³(cos²(θ))(sin²(θ)) dr dθ
= ∫[0,2π] ∫[1,2] r³cos²(θ)sin²(θ) dr dθ
To evaluate this integral, we can use the property cos²(θ)sin²(θ) = (1/4)sin²(2θ), so the integral becomes:
V = (1/4) ∫[0,2π] ∫[1,2] r³sin²(2θ) dr dθ
Now, we integrate with respect to r:
V = (1/4) ∫[0,2π] [(1/4)r⁴sin²(2θ)] [1,2] dθ
= (1/4) ∫[0,2π] [(1/4)(2⁴ - 1⁴)sin²(2θ)] dθ
= (1/4) ∫[0,2π] [(15/4)sin²(2θ)] dθ
= (15/16) ∫[0,2π] [1 - cos(4θ)]/2 dθ
= (15/32) [θ - (1/4)sin(4θ)] [0,2π]
= (15/32) [2π - (1/4)sin(8π) - 0 + (1/4)sin(0)]
= (15/32) (2π - 0)
= 15π/16
learn more about Volume of solid here:
https://brainly.com/question/32140285
#SPJ4
Please answer correctly !!!!!!!! Will mark brainliest !!!!!!!!!!!!

Answers
2 - x + 6 - 1 + y - x
Answer: 7 - 2x + y
