If the average price of a new one-family home is $246,300 with a standard deviation of $15,000, find the minimum and maximum prices of the houses that a contractor will build to satisfy the middle 60% of the market. Assume that the variable is normally distributed.

Answer: Show the table

Step-by-step explanation:

SHow the table

Answer:

\( \frac{25}{2} \)

Step-by-step explanation:

Given 15 ÷6/5

\(15 \div \frac{6}{5} \\ = > 15 \times \frac{5}{6} \\ = > 5 \times \frac{5}{2} \\ = > \frac{25}{2} \\ therefore \: the \: answer \: is \: \frac{25}{2} \\ this \: is \: because \: it \: cannot \: be \: broken \: down \: into \: lowest \: term \: again\)

6.3 units

The formula for calculating the distance between two points is given as:

Given the following coordinate points

A(2,4) and B(8,2)

Substitute the given parameters into the formula to have:

Hence the distance between the points (2,4) and (8,2) round to the nearest tenth is 6.3 units

Answer:

\(\frac{24}{7}\)

Step-by-step explanation:

Tanθ=Opposite/Adjacent

we have the adjacent side but need the oppsoite

We will use a²+b²=c²

25²=7²+b²

576=b²

b=24

Therefore the answer is

\(\frac{24}{7}\)

Answer:

Step-by-step explanation:

The standard error of the mean is defined as the ratio of standard deviation to the square root of the sample size of a data. The standard error of the mean is mathematically expressed as shown below;

\(X = \frac{\sigma}{\sqrt{n} }\)

X is the standard error of the mean

\(\sigma\) is the standard deviation

n is the sample size.

Given;

\(\sigma = 121\\n = 256\)

On substitution into the formula we have;

\(X = \frac{121}{\sqrt{256} }\)

\(X = \frac{121}{16} }\\\)

X ≈ 7.56

The length of BD is 18.5 units.

In the given right triangle ABC, with altitude BD drawn to hypotenuse AC, we are given the lengths AD = 22 and DC = 15. We need to find the length of BD.

Let's consider triangle ABD. Since BD is the altitude, it divides the right triangle ABC into two smaller right triangles: ABD and CBD.

In triangle ABD, we have the following sides:

AB = AD = 22 (given)

BD = ?

Now, let's consider triangle CBD. In this triangle, we have the following sides:

BC = DC = 15 (given)

BD = ?

Since triangles ABD and CBD share the same base BD, and their heights are the same (BD), we can say that the areas of these triangles are equal.

The area of triangle ABD can be calculated as:

Area(ABD) = (1/2) * AB * BD

Similarly, the area of triangle CBD can be calculated as:

Area(CBD) = (1/2) * BC * BD

Since the areas of ABD and CBD are equal, we can equate their expressions:

(1/2) * AB * BD = (1/2) * BC * BD

We can cancel out the common factor (1/2) and solve for BD:

AB * BD = BC * BD

Dividing both sides of the equation by BD (assuming BD ≠ 0), we get:

AB = BC

In triangle ABC, the lengths AB and BC are equal, which implies that triangle ABC is an isosceles right triangle. In an isosceles right triangle, the leg's length are congruent, so AB = BC = AD = DC.

BD is equal to half of the hypotenuse AC:

BD = (1/2) * AC

Substituting the given values, we have:

BD = (1/2) * (AD + DC) = (1/2) * (22 + 15) = (1/2) * 37 = 18.5

Therefore, the length of BD is 18.5 units.

For more questions on length

https://brainly.com/question/28322552

#SPJ8

Remove the parentheses and add like terms:

Answer:

Step-by-step explanation:

(A)  subtract larger arc and smaller arc, divide by 2 and that gives angle

<VYX =(1/2)(VW-VX)

<VYX = (1/2)(145-51)

<VYX =(1/2)(94

<VYX = 47

(b) The 2 arcs added then divided by 2 = angle in middle

<AEB=(1/2)(CD+AB)

69 = (1/2)(CD+87)

138=CD+87

CD=51

Answer:

33 units²

Refer to the attached page

I've shown the complete calculation over there.

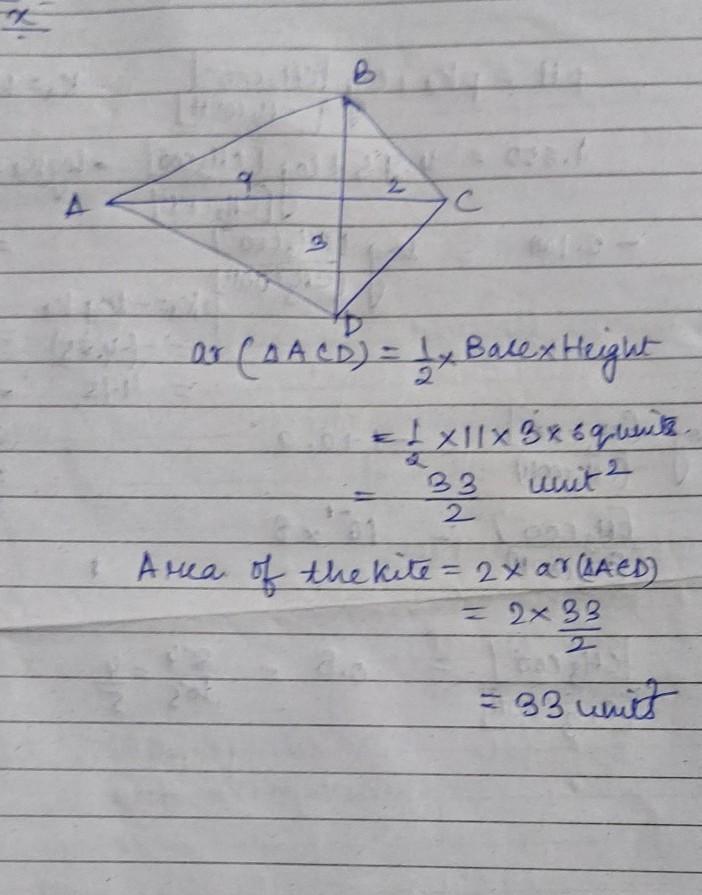
Answer: 33

Step-by-step explanation:

one easy way to do it is by finding the area of the 4 triangles.

because the top two and the bottom two are the same that helps a lot. The first triangle is 9 times three and then cut your answer in half. Do the same thing for the other 9 times three triangle you will end up with 27. for the top two you would multiply 3 times two to get 6 cut 6 in half to get 3. do the same or the other triangle and now you just have to add.

3 plus 3 plus 13.5 plus 13.5

to get 33

Answer:

distance(miles) = number of hours driven * 55

Step-by-step explanation:

Answer:

She needs 16 recipe to make 8 gallons

Answer:

Step-by-step explanation:

18-5=13

18-9=9

Answer:

today

Step-by-step explanation:

ez  " what would tomorrow's yesterday's tomorrow be?" this is telling us that we are thinking about yesterday

if we were to add a day to yesterday lets say its the first it would be the second lets say we were the 3rd and we add one day to yesterday we would call it today

Answer:

\(\displaystyle \frac{1}{\pi}\approx0.318\)

Step-by-step explanation:

The velocity of an object moving on a line is given by the function:

\(\displaystyle v(t)=\frac{1}{\pi}+\sin(3t),\; \frac{\pi}{2}\leq x\leq\pi\)

And we want to determine the velocity of the object when its acceleration is 3.

So, we will need to determine our acceleration function. Remember that acceleration is simply the derivative of speed. Therefore, our acceleration function a(t) will be:

\(\displaystyle a(t)=v^\prime(t)=\frac{d}{dt}[\frac{1}{\pi}+\sin(3t)]\)

Differentiate. We will use the chain rule on the second part. Hence, our acceleration function is:

\(\displaystyle a(t)=3\cos(3t)\)

We want to find the velocity when the acceleration is 3.

So, let’s set a(t) equal to 3 and determine at what time t our function equals 3. Hence:

\(3=3\cos(3t)\)

Divide both sides by 3:

\(\cos(3t)=1\)

Take the inverse cosine of both sides.

Remember that cosine is 1 for every 2π. Hence:

\(3t=2\pi n\)

Where n is an integer.

Divide both sides by 3. Therefore, our solutions are:

\(\displaystyle t=\frac{2\pi n}{3}\)

However, our domain was π/2≤x≤π.

Hence, we can test values of n such that it is within our domain.

Testing for n=0, 1, and 2, we see that:

\(\displaystyle t=0, \, t=\frac{2\pi}{3},\, t=\frac{4\pi}{3}...\)

However, the only solution that is within our domain is the second solution.

Hence, the acceleration is 3 when the t is 2π/3.

Therefore, our velocity at that time t is:

\(\begin{aligned}\displaystyle v(\frac{2\pi}{3})&=\frac{1}{\pi}+\sin(3(\frac{2\pi}{3}))\\ &=\frac{1}{\pi}+\sin(2\pi)\\&=\frac{1}{\pi}+0\\&=\frac{1}{\pi}\approx 0.318\end{aligned}\)

Answer:

i think it might be C

Step-by-step explanation:

a) There are 2 x 2 = 4 sample points in the sample space

b) Tree Diagram

O D.\nH\nHe\nT\nH\nT\n

Sample space: D. HH, HT, TH, TT

c) P(no tails) = P(HH)

= 1/4

d) P(exactly one tail) = P(HT, TH)

= 2/4

= 1/2

e) P(2 tails) = P(TT)

= 1/4

f) P(at least one tail) = P(HT, TH, TT)

= 3/4

In mathematics, tree diagrams are often used in probability and statistics to show all the possible outcomes of an event. In computer science, they are used to represent the hierarchical structure of files and directories in a file system

Read more about probability here:

https://brainly.com/question/24756209

#SPJ1

The number of people that nare expected to vote in the election is 260,000. people.

Simply put, a fraction is a portion of a whole. Mathematically, the number is represented as a quotient with split numerator and denominator. The numerator and denominator of a simple fraction are both integers. On the other hand, a complex fraction has a fraction in either the numerator or the denominator.

In this situation, the pre-election survey showed that two out of every three eligible voters would cast ballots in the county election and there are 390,000 eligible voters in the county.

The number of people expected to vote will be:

= Fraction of expected voters × Total number of people

= 2/3 × 390000

= 2 × 130000

= 260000

Learn more about fractions on:

brainly.com/question/78672

#SPJ1

Answer:

it would probably be t series

Answer:

mutiply

Step-by-step explanation:

Answer:

0.674 means that it 674/1000

Step-by-step explanation:

which mean that if the model consist of 1000 squares, you have to shade 674 of the squares.

If the model consist of 100 squares, you have to shade 337 of the squares  ( you get the number after dividing both 674 and 1000 with 2)

A catering business must generate $611,473 in sales to make a 10 percent profit, which is also the break-even point for this operation.

To determine the sales needed to make a 10 percent profit and the break-even point for the catering business, we can utilize the concept of contribution margin.

The contribution margin is the amount remaining from sales revenue after deducting variable costs.

Let's denote the sales needed to make a 10 percent profit as "S."

The contribution margin can be calculated by subtracting the variable operating costs from the sales revenue.

In this case, the variable operating costs are $245,650.

Therefore, the contribution margin is S - $245,650.

To calculate the break-even point, we need to consider the point at which the business neither makes a profit nor incurs a loss.

At the break-even point, the total revenue generated will exactly cover both the variable and fixed costs.

The fixed operating costs are given as $365,823.

Thus, the equation for the break-even point can be expressed as:

S - $245,650 - $365,823 = 0.

By rearranging the equation, we find:

S = $245,650 + $365,823

S = $611,473

Therefore, the catering business needs to generate $611,473 in sales to make a 10 percent profit.

This amount will also be the break-even point, as it covers all the variable and fixed costs without resulting in a profit or loss.

For similar question on percent profit.

https://brainly.com/question/31618610  

#SPJ8

Answer:

\(\frac{dy}{dx} =-\sqrt[3]{\frac{y}{x} }\)

Step-by-step explanation:

Recall that using the chain rule we can state:

\(\frac{dy}{dt} =\frac{dy}{dx}*\frac{dx}{dt}\)

and therefore solve for dy/dx as long as dx/dt is different from zero.

Then we find dy/dt  and dx/dt,

Given that

\(x=sin^3(t)\\dx/dt = 3 sin^2(t)* cos(t)\)

And similarly:

\(y=cos^3(t)\\dy/dt=-3\,cos^2(t)*sin(t)\)

Therefore, dy/dx can be determined by the quotient of the expressions we just found:

\(\frac{dy}{dx} =\frac{dy/dt}{dx/dt} =\frac{-3\,cos^2(t)*sin(t)}{3\,sin^2(t)*cos(t)} =-\frac{cos(t)}{sin(t)}\)

now notice that we can find   \(cos(t) = \sqrt[3]{y}\)  from the expression for y,

and   \(sin(t) = \sqrt[3]{x}\)  from its expression for x.

Therefore dy/dx can be written in terms of x and y as:

\(\frac{dy}{dx} =-\frac{cos(t)}{sin(t)}=-\sqrt[3]{\frac{y}{x} }\)

Answer:

208 cubic units

Step-by-step explanation:

The composite figure in the picture is composed of a triangular prism and a rectangular prism, both which can be calculated by the base * height formula.
First, let’s calculate the volume of the triangular prism:

The base is the area of the triangle base, which is dc/2, or 4*3/2, which is 6. Next, multiply the area of the base by the height “b”: 6 * 8 = 48.

Now, let’s calculate the volume of the rectangular prism:

The base is the rectangular base’s area, which is a*c, or 5*4, which is 20. Next multiply the base by the height “b”: 20 * 8 = 160

Now, add up the volumes of the rectangular and triangular prisms:

160 + 48 = 208 cubic units

Answer:

-y+11

Step-by-step explanation:

Answer:-1y + 11

Step-by-step explanation:

7y + 5 - 8y + 6

-simplify

7y - 8y = -1y

5+6=11

= -1y + 11

Answer:

\(2^{-4}\) = 1/16

\(6^{-5}\) × \(6^{5}\) = 1

Step-by-step explanation:

\(2^{-4}\) = 0.0625

0.0625 = 1/16

\(6^{-5}\) × \(6^{5}\) = 1

Step-by-step explanation:

The situation described can be modeled using a linear equation, where the balance of the savings account increases by a fixed amount every month. Specifically, the equation that represents this situation is:

balance = $5000 + $825 * months

where "months" represents the number of months that have passed since the account was opened. The slope of this line is constant at $825, indicating that the balance is increasing by the same amount every month.

Therefore, the model for this situation is linear.

The table with correct values of A, B and C is,

⇒ Donuts   2        4        5        8

    Cost     13.80 27.60 34.50 55.20

A ratio indicates how many times one number contain in another number. The ratio of two number is written as x : y, which is equivalent to x/y. Where, x and y are individual amount of two quantities. And, Total quantity gives after combine as x + y.

We have to given that;

The table below shows the ratios of boxed donuts to the cost.

Donuts    A       4        5     C

Cost    13.80  27.60   B   55.20

Now, By definition of ratio, we get;

⇒ A / 13.80 = 4 / 27.60

⇒ A = 13.80 × 4 / 27.60

⇒ A = 2.00

And,

⇒ 4 / 27.60 = 5 / B

⇒ B = 5 × 27.60 / 4

⇒ B = 34.5

⇒ 4 / 27.60 = C / 55.20

⇒ C = 55.20 × 4 / 27.60

⇒ C = 8

Thus, The table with correct values of A, B and C is,

⇒ Donuts   2        4        5        8

    Cost     13.80 27.60 34.50 55.20

Learn more about the ratio visit:

https://brainly.com/question/12024093

#SPJ1

Answer:

a

Step-by-step explanation:

i took the test :)

Answer:

1. similar

2. different

3, 2/5

The amount that you will have in 3 years, given the interest rate and the amount won, is 1, 195, 618. 17 currency units

To find the amount earned in three years as a result of your lottery being invested, use the future value formula which is:

= Amount won x ( 1 + periodic  rate ) ^ number of periods

Periodic rate :

= 6 % / 4 quarters per year

= 1. 5 %

The number of periods is:

= 3 years x 4 quarters per year

= 12 quarters

The amount you will have in 3 years is:
= 1,000,000 x ( 1 + 1. 5 %) ¹²

= 1, 195, 618. 17 currency units

Find out more on compounding quarterly at https://brainly.com/question/2455673

#SPJ1

Answer:

688.19 inches

Step-by-step explanation: