If you flip the graph of the absolute value parent function, f(x)=|x|, over the x-axis, what is the equation of the new function?
Answers
The equation of the new function is f'(x) = -|x|
How to determine the equation of the new function?The function is given as:
f(x) = |x|
The rule of flipping the graph over the x-axis
(x, y) = (x, -y)
So, we have:
f'(x) = -f(x)
Substitute f(x) = |x|
f'(x) = -|x|
Hence, the equation of the new function is f'(x) = -|x|
Read more about function transformation at:
https://brainly.com/question/13810353
#SPJ1
Related Questions
Multiply the polynomial
(4x2-4)(2x+1)
PLEASE HELP!!! ASAP!!!
Answers
Answer:
4(2x^3+ x^2-2x-1)
Step-by-step explanation:
the explanation is given above in the picture
pls do mark me the brainliest.

Answer:
4(2x^3+x^2-2x-1)
Step-by-step explanation:
Mulitply each term:
8x^3+4x^2-8x-4
Now simplify: 4(2x^3+x^2-2x-1)
Please mark me brainliest!!
a manufacturing machine has a 5% defect rate. if 7 items are chosen at random, what is the probability that at least one will have a defect?
Answers
The probability of selecting at least one defective item at random is 0.3017.
The probability of an event occurring at least once will be calculated as the complement of the probability of the event never occurring. You can use exponents to multiply the number of events that occurred when calculating this amount.
Defect rate = P(defect) = 0.05
Probability is defined as the required outcome divided by the total number of possible outcomes.
P( at least 1 is defective) = 1 - P(none is defective)
P(not defective) = 1 - P(defective) = 1 - 0.05 = 0.95
P(none is defective) = P(non defective)^7
P(none defective) = 0.95× 0.95 × 0.95 × 0.95 × 0.95× 0.95× 0.95=0.6983
P(at least one is defective) = 1 - 0.6983 = 0.3017
Therefore, probability of at least one defective item is 0.3017.
For more information on Probability, visit :
https://brainly.com/question/11443428
#SPJ4
Mathematical methods that allow us to determine whether we can generalize findings from our sample to the full population are called.
Answers
Statistical inference methods. These methods help us determine if findings from a sample can be generalized to the full population by using mathematical techniques to make inferences about population parameters based on sample data.
Mathematical methods that allow us to determine whether we can generalize findings from our sample to the full population are called statistical inference methods. These methods involve making inferences and drawing conclusions about population parameters based on sample data. Statistical inference helps us make statements about the population based on the information obtained from a representative sample. Common techniques in statistical inference include hypothesis testing, confidence intervals, and estimation.
learn more about Statistical inference methods here:
https://brainly.com/question/30881181
#SPJ11
Can someone please give me the (Answers) to this? ... please ...
I need help….

Answers
Answer:
1. C. 8.06
2.
a: obtuse
b: acute
3. 50 miles
\(48^{2} +14^{2} = c^{2}\)
\(2304 + 196 = c^{2}\)
\(2500 = c^{2}\)
\(\sqrt{2500} = \sqrt{c}\)
\(50 = c\)
the length of a rectangle is six times its width. if the perimeter of the rectangle is , find its area.
Answers
If the perimeter of the rectangle is given, then we can find the sum of all sides, which is 2 times the length plus 2 times the width.
Perimeter = 2l + 2w = 2(6w) + 2w = 14w
Given perimeter = 28
So, 14w = 28, which means w = 2. Then, l = 6w = 12.
Therefore, the area of the rectangle is A = l x w = 12 x 2 = 24 square units.
To find the area of a rectangle, we need to know both the length and width. In this case, we are given a relationship between the length and the width of the rectangle. Specifically, the length is six times the width, or l = 6w.
We are also given the perimeter of the rectangle. The perimeter is the sum of all four sides of the rectangle, which is 2 times the length plus 2 times the width. So, we can write:
Perimeter = 2l + 2w
Substituting l = 6w, we get:
Perimeter = 2(6w) + 2w = 14w
We are told that the perimeter of the rectangle is 28, so we can set 14w equal to 28 and solve for w:
14w = 28
w = 2
Once we know the value of w, we can find the value of l:
l = 6w = 6(2) = 12
Now that we know both the length and the width, we can calculate the area of the rectangle:
A = l x w = 12 x 2 = 24
Therefore, the area of the rectangle is 24 square units.
Learn more about rectangle here: brainly.com/question/15019502
#SPJ11
In a games shop, a board game that normally sells for $25 is marked ‘10% off’. What is the discount on the game? What is the new sale price?
Answers
Answer:
Discount is $2.50
Sale price is $22.50
Step-by-step explanation:
You can write 10% as 0.10.
Figure out the discount.
$25 x 0.10 = $2.50
The discount is $2.50
The new sale price is the original (normal) price minus the discount.
$25 - $2.50 = $22.50 is the new sale price
How tall is the school?

Answers
Suppose two vectors point in opposite directions. This means their cross product must be zero. True or false?
Answers
It is true if two vectors point in opposite directions. This means their cross product must be zero.
What is cross product?Cross product is a vector product of two vectors in the three dimensional vector space.
In the case when the two vectors point in opposite directions so there cross product should be zero.
Impact on two points:
In the case when the two vectors point in opposite directions so there cross product should be zero.
Like
A*B = [A][B] sin
Here theta is be the angle that lies between them
So,
A*B = [A][B] sin 180
So, A*B = 0
hence, the given statement is true.
learn more about vectors here:
brainly.com/question/21797532
#SPJ4
What is the vertex of the graph of f x )=[ x 5 ]- 6?
Answers
The vertex of the graph of f(x) = |x - 5| - 6 is (5, -6). It lies in the fourth quadrant.
Therefore the answer is (5, -6).
The graph f(x) = |x - 5| - 6 is symmetrical about the axis x = 5.
A vertex of a graph is a node of a graph. For a graph of the form f(x) = a|x - h| + k, the vertex is (h, k). So in this case where f(x) = |x - 5| - 6, a = 1, h = 5 and k = -6. Therefore the vertex of the given graph f(x) is
(5, -6)
We can observe that was added 5 units to the x, that is, a negative translation through the horizontal axis. So, our function is located at x = -5, because a horizontal translation to the left is when we add to the x certain units.
Then, we observe that the function subtracted 6 units to the vertical variable, that is, the function is translated 6 units downside.
Therefore, our functions is locate in (-5;-6), it starts there, which is the vertex.
--The question is incomplete, answering to the question --
"What is the vertex of the graph of f(x) = |x - 5| - 6?"
To know more on vertex here
https://brainly.com/question/6248714
#SPJ4
heyy! i’ll give brainliest help asap pls

Answers
Answer:
I'm not sure if its A or C but C sounds like it could be the right answer
Step-by-step explanation:
Answer: Planting vegations near riverbanks
Step-by-step explanation:
because everything else is harmful to the earth .-.
Find a unit vector normal to the surface ze^(x2−y2) = 3 at (1,1,3). Also find the standard form of the equation of the tangent plane at the given point.
Note that there are two expressions for the unit normal that differ by a minus sign. To fix a unique answer we give the coefficient of the k component.
Similarly, the equation of the tangent plane ax + by + cz + d =0 is only unique up to a constant multiple. In order to clarify your answer we give the coefficient of the z so that there is a unique solution.
Unit normal: N=____i+____j + 1/√73k Tangent Plane: __x + __y + z – 3 = 0
Answers
Unit normal: N= 2i+3j + 1/√73k
The standard form of the equation of the tangent plane at (1,1,3) is x - 4y + z - 3 = 0.
To find the normal vector, we first need to find the partial derivatives of the surface equation with respect to x and y. Using the chain rule, we get:
∂z/∂x = 2xe^(x²−y²) ∂z/∂y = -2ye^(x²−y²)
At the given point (1,1,3), these partial derivatives evaluate to:
∂z/∂x = 2e^0 = 2 ∂z/∂y = -2e^0 = -2
So the gradient vector of the surface at (1,1,3) is:
grad(z) = <2, -2, ze^(x²−y²)> = <2, -2, 3>
To find a unit normal vector, we need to divide the gradient vector by its magnitude:
|grad(z)| = √(2² + (-2)² + 3²) = √(17 + 9 + 4) = √(30)
So the unit normal vector is:
N = (1/√(30)) <2, -2, 3> = (1/√(30)) <2, -2, 3>
Note that there are two possible unit normal vectors, since we could also multiply this vector by -1.
Now we need to find the equation of the tangent plane. We know that the tangent plane has the form:
ax + by + cz + d = 0
where (a, b, c) is the normal vector we just found, and (x, y, z) is any point on the plane. We also know that the plane passes through the point (1,1,3), so we can substitute these values into the equation to get:
a(1) + b(1) + c(3) + d = 0
Simplifying this equation, we get:
a + b + 3c + d = 0
To fix a unique solution, we are given the coefficient of the z component, which is 1. So we can set c = 1 and solve for the other coefficients:
a + b + 3 = 0 a + b = -3
We can choose any values for a and b that satisfy this equation, as long as they are not both zero. For example, we can choose a = 1 and b = -4, or a = -3 and b = 0. Either way, we get:
Tangent plane: x - 4y + z - 3 = 0
To know more about vector here
https://brainly.com/question/29740341
#SPJ4
Shade ______ line
for greater than (>).
Answers
\(above \: the \: line\)
Each side of a square painting is 6 feet long. A frame shop charges $2.21 per foot for a metal frame. How much would it cost to buy a frame for the painting?
Answers
A frame shop charges $2.21 per foot for a metal frame, it would cost approximately $53.04 to buy a frame for the painting.
We must calculate the square's perimeter and multiply it by the frame's price per square foot in order to establish the cost of purchasing a frame for the square artwork.
Since a square's sides are all equal, the perimeter of the square painting can be calculated as follows:
Perimeter = 4 * side length
Given,
Side = 6 feet
Perimeter = 4 * 6 = 24 feet
Cost = Perimeter * Cost per foot
Cost = 24 * $2.21
Cost ≈ $53.04
Thus, the answer is $53.04.
For more details regarding perimeter, visit:
https://brainly.com/question/7486523
#SPJ1
Which property is illustrated by this problem? 99.78 + 0 = 99.78
Answers
Answer:
Identity property of addition.
Step-by-step explanation:
The identity property of addition says that the sum of 0 and any number is that number. So 99.78 + 0 = 99.78 is identity property of addition. This is true because the definition of 0 is "no quantity", so when we add 0, the number doesn't change.
Rewrite one eighteenthx3y + seven eighteenthsxy2 using a common factor.
one thirdxy(6x2 + 7y)
one thirdx2y(6x2 + 9y)
one eighteenthxy(x2 + 7y)
one eighteenthx3y2(y + 7)
Answers
Answer:
C
Step-by-step explanation:
1/18 x³y + 7/18 xy²
1/18 xy (x² + 7y)
when we use the word automobile to refer to a category of transport vehicles, we are using this word as a(n)
Answers
When we use the word automobile to refer to a category of transport vehicles, we are using this word as a concept. The correct answers is concept
A concept is an abstract idea that takes form in your mind. This is known as the structures of thoughts and beliefs. They are important because it gives a clear explanation of a particular subject.
An automobile, byname auto, also called motorcar or car, a usually four-wheeled vehicle designed primarily for passenger transportation and commonly propelled by an internal-combustion engine using a volatile fuel, this term is generally used for an vehicle when refering to its category.
When we think of the word automobile, the first thing that comes to your mind is a category of transport. The mind connects the thoughts around the structures build. That’s a concept
Thus, when we use the word automobile to refer to a category of transport vehicles, we are using this word as a concept.
To learn more about abstract idea refer here
https://brainly.com/question/13291061
#SPJ4
Math school please need help

Answers
Answer:
r² = (9 - 4)² + (6 - 4)² = 5² + 2² = 25 + 4 = 29
So the equation of this circle is
(x - 4)² + (y - 4)² = 29
Translate algebraic words to symbols.
Six times y divided by x squared
A. 6y - X2
B. 6y + 2x
C. (6 + y)/2x
D. 6y/x2

Answers
Answer:
D
Step-by-step explanation:
Answer:
D. 6y/x²
Step-by-step explanation:
6×y= 6y
x squared =x²
charlotte denning earns both $13/hour and $26 for every sale she completes. during the most recent week, she worked 47 hours and made a total of 71 sales.
Answers
Answer: nice for her
Step-by-step explanation:
NEED HELP ASAP! will rate 5 stars!!

Answers
The answer is C cause it makes ore sense against the other answers
Greatest common factor
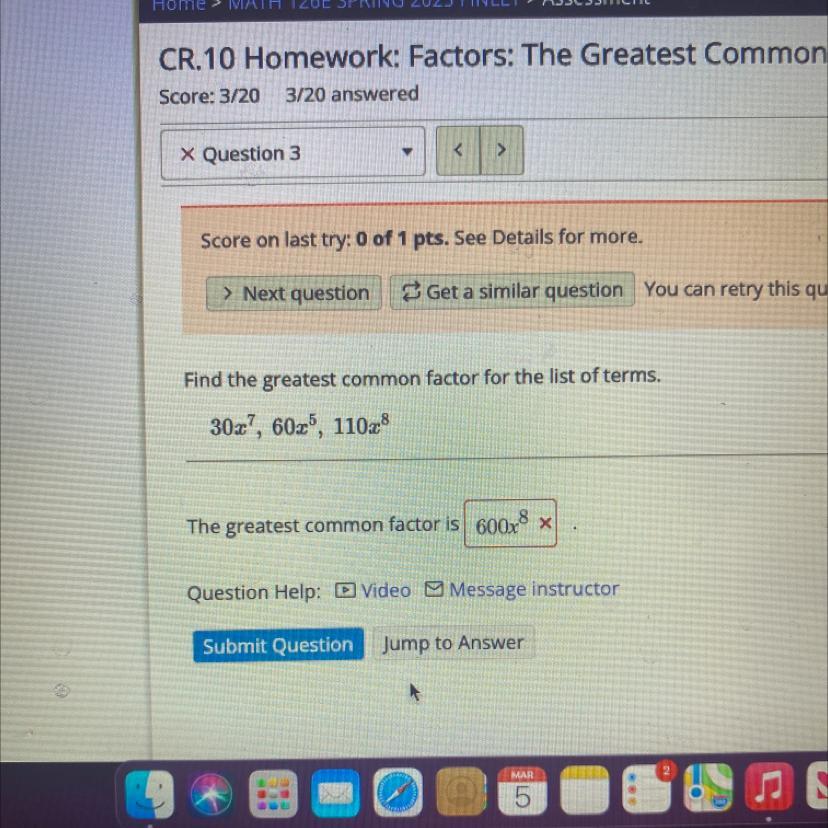
Answers
Answer:
10\(x^{5}\)
Step-by-step explanation:
The list is: 30\(x^{7}\), 60\(x^{5}\), 110\(x^{8}\)
Find the GCF
We see
30, 60, and 110 have the greatest common factor is 10.
\(x^{7}\), \(x^{5}\), \(x^{8}\) have the greatest common factor is \(x^{5}\)
So, the greatest common factor for the list of terms is 10 \(x^{5}\)
Simplify this expression:
4(1 - 3x) + 7 x - 8
Answers
4(1-3x) + 7x -8
Use distributive property:
4 -12x + 7x -8
Now combine like terms:
-5x -4
Answer:
\(-5x-4\)
Step-by-step explanation:
With the expression \(4(1-3x) + 7x - 8\), we can simplify it down by applying the distributive property, then combining like terms.
\(4(1-3x)+7x-8\\\\4-12x+7x-8\\\\4-5x-8\\\\-5x-4\)
Hope this helped!
Which of the following has a value between 10 over three and 11 over three
Answers
1/2 w + 2 ; w = 1/9 what is the answer because i have been on this problem for an hour
Answers
Answer:
its -1/5
Step-by-step explanation:
Answer:
Step-by-step explanation:
1/2 (1/9) + 2=
1/18 + 2=
2 1/18
How do you check if an inverse is a function?
Answers
If a value of y relates only to one value of x, then the function does have an inverse function.
Define the term function and its inverse?A relation between such a collection of inputs and outputs is known as a function.
A function is, to put it simply, a connection between inputs in which each input is connected to precisely one output. Each function has a range, codomain, and domain. The usual way to refer to a function is as f(x), where x is just the input.If and only if the outcome of reflecting a function's graph about the line y = x is the function's graph, then the function f does have an inverse (passing from the vertical line test).Thus, if a value of y relates only to one value of x, then the function does have an inverse function.
To know more about the function and its inverse, here
https://brainly.com/question/3831584
#SPJ4
the area of a circle is 25 ft. what is the circumference of the circle?
Answers
Answer: Circumference would be 17.72
Step-by-step explanation:
Formulas for area and circumference:
A=πr2
C=2πr
Which would look like this for your problem:
2·\(\sqrt{\pi*\\25}\)≈17.72454
Round up 17.72454 to 17.72
There's your answer, hope this helps
Suppose $P$ is the point $(5,3)$ and $Q$ is the point $(-3,6)$. Find point $T$ such that $Q$ is the midpoint of segment $\overline{PT}$.
help qwikly
Answers
Answer:
(1,4.5)
(\(\frac{5+(-3)}{2} ,\frac{3+6}{2}\))
Suppose we create a box model for the outcome of a game of darts. The player has a 1/3 chance of throwing a dart in the inner ring, and a 2/3 chance of the dart landing in the outer ring. In our model, we have two unique tickets marked "inner" and "outer." We put in 1 ticket marked "inner." How many tickets do we put in that are marked "outer?"
a. 0
b. 1
c. 2
d. 3
Answers
As per the combination method, the number of tickets that we put in that are marked "outer" is 3 (option d).
In this case, we want to choose the number of tickets marked "outer." Let's call this number k. We know that we already put one ticket marked "inner" in the box, so the total number of tickets in the box is 2. Therefore, n = 2.
Now we need to determine k. We want to know how many tickets we need to put in that are marked "outer." We can represent this as a. So we have:
ᵃC₁ = a! / ((1!)(a-1)!) = a
We want to find the value of a that satisfies the condition that the probability of choosing an "inner" ticket is 1/3 and the probability of choosing an "outer" ticket is 3/2.
Since we already put in 1 ticket marked "inner," the probability of choosing an "inner" ticket is 1/2, which means the probability of choosing an "outer" ticket is also 1/2.
We know that the probability of choosing an "outer" ticket is 3/2, so we can set up the following equation:
ᵃC₁ / 2 = 3/2
Solving for a, we get:
a = 3
In conclusion, the answer is (d) 3.
To know more about combination here
https://brainly.com/question/28998705
#SPJ4
Find the minimum and maximum value of the functiony=(x−9)²+9. Enter infinity or -infinity if thefunction never stops increasing or decreasing.Maximum value =Minimum value =
Answers
The minimum value of the function is 9, and the function never stops increasing.
The given function is y=(x−9)²+9.
We need to find the minimum and maximum value of the function. The given function is a quadratic function whose graph is a parabola. Since the coefficient of x² is positive, the graph of the quadratic function will be in the form of an upward parabola whose vertex is at the point (h,k).
The vertex form of the quadratic function is given byy = a(x - h)² + k, where(h,k) is the vertex of the parabola.
a is the coefficient of (x - h)².
In the given function,y = (x-9)² + 9, the vertex of this function is (9,9) and a=1.
Therefore, the minimum value of the function is 9 at x=9, which is the vertex of the parabola.
The function y=(x−9)²+9 is an upward parabola, and hence it never stops increasing, which means that the function has no maximum value.
Thus, the minimum value of the function is 9, and the function never stops increasing.
To know more about minimum value refer here:
https://brainly.com/question/12321880
#SPJ11
Calculate the costs of these home improvement and maintenance costs.
Annual real estate taxes on a property are $2046. Insurance premiums total $1236. Required flood insurance protection premiums are $380 annually. The county assesses an annual special assessment landfill fee of $125. Trash collection costs $65 quarterly. Annual homeowner's association is $720 for common area maintenance of the subdivision. The pool company charges $45 quarterly to maintain the pool. Ongoing termite and pest protection costs $39 monthly. How much should a buyer save each month to cover these fees?
Answers
Answer: To calculate the total amount a buyer should save each month to cover these fees, we need to add up all the costs and divide by 12 (the number of months in a year).
Annual real estate taxes = $2046
Insurance premiums = $1236
Flood insurance premiums = $380
Annual special assessment landfill fee = $125
Quarterly trash collection costs = $65 x 4 = $260
Annual homeowner's association fee = $720
Quarterly pool maintenance costs = $45 x 4 = $180
Monthly termite and pest protection costs = $39 x 12 = $468
Total annual costs = $2046 + $1236 + $380 + $125 + $260 + $720 + $180 + $468 = $5405
Total monthly costs = $5405 / 12 = $450.42
Therefore, a buyer should save $450.42 each month to cover these fees.
Step-by-step explanation: