In Northern California, Oceana's scientists tested 89
samples of fish labeled as snapper, and 38 came back
as rockfish. What's the experimental probability of buying
snapper mislabeled as rockfish?
Answers
The experimental probability of buying snapper mislabeled as rockfish is 0.427.
What distinguishes theoretical from experimental probability?The chance of an event based on real results from an experiment or observation is known as experimental probability. It is derived by subtracting the total number of trials from the number of times the event happened. The likelihood of an event based on mathematical analysis or reasoning is known as theoretical probability, on the other hand. It is computed by dividing the total number of outcomes by the number of ways the event might happen. While experimental probability considers real possibilities that might not be equally likely, theoretical probability is predicated on the idea that all alternatives are equally likely.
Given that, total fish = 89 and mislabeled fish = 38, thus:
P(mislabeled as rockfish) = 38/89 ≈ 0.427
Hence, the experimental probability of buying snapper mislabeled as rockfish is 0.427.
Learn more about experimental probability here:
https://brainly.com/question/3733849
#SPJ1
Related Questions
IV Find the citical points at which profit (pie) is maximized given the total revenue TR=4700−302 and Total CostTC =320/10,500 (2pts) 1. Compute Marginal Revenue and Marginal Cost 2. Equate MR=MC to find Q
∗
3. Verify that Q* is a relative maximum point 4. Compute the maximum profit level (pie) )
∗
by establishing (pie)* =9( (pie) (Q
∗
)
Answers
To find the critical points at which profit is maximized given the total revenue TR = 4700 - 302 and total cost TC = 320/10,500, we need to compute the marginal revenue and marginal cost, equate MR = MC to find the optimal quantity Q∗, verify if Q∗ is a relative maximum point, and compute the maximum profit level (π) by evaluating π∗ = 9(π(Q∗)).
Marginal Revenue (MR) is the derivative of the total revenue function with respect to quantity (Q). In this case, MR = dTR/dQ. By taking the derivative of TR = 4700 - 302 with respect to Q, we can find the expression for MR.
Marginal Cost (MC) is the derivative of the total cost function with respect to quantity (Q). In this case, MC = dTC/dQ. By taking the derivative of TC = 320/10,500 with respect to Q, we can find the expression for MC.
To find the optimal quantity Q∗, we equate MR and MC by setting MR = MC and solve for Q. This is because profit is maximized when MR equals MC.
Once we have found Q∗, we need to verify if it is a relative maximum point. This can be done by checking the second derivative of the profit function and determining if it is negative at Q∗. If the second derivative is negative, it confirms that Q∗ is a relative maximum point.
Finally, to compute the maximum profit level (π∗), we evaluate π(Q∗) by substituting Q∗ into the profit function. In this case, we can multiply the value of π(Q∗) by 9 to obtain the maximum profit level (π∗).
Learn more about relative maximum point here:
https://brainly.com/question/32310828
#SPJ11
Chile please help me cuz I’m lost ash

Answers
Answer:
1. acute angle, 2.right angle, 3.obtuse angle
Step-by-step explanation:
I If the game with 3 hits is considered to be recorded in error, it might be removed from the data set. If that happens a. What happens to the mean of the data set? b. What happens to the median of the data set? plot data- 2(0) 3(1) 4(0) 5(0) 6(0) 7(2) 8(4) 9(5) 10(4) 11(4) 12(0) 13(0) .please help
Answers
Answer:
If the game with 3 hits is ignored the data becomes:
7, 7, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 10, 10, 11, 11, 11, 11a) The mean will increase.
With 3:
(3 + 7*2 + 8*4 + 9*5 + 10*4 + 11*4)/20 = 8.9Without 3:
(7*2 + 8*4 + 9*5 + 10*4 + 11*4)/19 = 9.21b) The median will remain as is.
With 3 and without the median is same = 9help me please . i hope to find a solution :((

Answers
Answer:
277.778 m/s
Step-by-step explanation:
just divide by 3.6
Determine which integers in the set S:{-4, 4, 6, 21) make the inequality 3(-5) > 3(7-2j)true.
OS:{6, 21}
OS:{4, 21}
OS:{-4, 6}
OS:{-4,4}
Answers
The integers in the set S that make the inequality 3(-5) > 3(7-2j) true are {-4, 6}.
To determine which integers in the set S = {-4, 4, 6, 21} make the inequality 3(-5) > 3(7-2j) true, we can simplify the inequality and compare the values.
First, let's simplify the inequality:
3(-5) > 3(7-2j)
-15 > 21 - 6j
Now, let's compare the values of -15 and 21 - 6j:
Since -15 is less than 21 - 6j, we can conclude that the inequality 3(-5) > 3(7-2j) is true.
Now, let's determine which integers in the set S satisfy the inequality. The integers in the set S that are less than 21 - 6j are:
-4 and 6
Therefore, the integers in the set S that make the inequality 3(-5) > 3(7-2j) true are {-4, 6}.
for such more question on inequality
https://brainly.com/question/17448505
#SPJ8
i need help if you can answer all please do

Answers
The z-score corresponds to 0.275 is -0.63.
The specific number of skateboards corresponding to the z-score from part (a) is 20,468.
We have,
(a)
To find the z-score corresponding to a specific percentage of days, we can use the standard normal distribution table or a calculator.
In this case, we are given that 45% of the days had a production of skateboards less than the specific value.
Since the standard normal distribution is symmetrical, we can find the z-score corresponding to 45% by finding the z-score that corresponds to
(1 - 0.45) / 2 = 0.275, which is the area to the left of the z-score.
Using the standard normal distribution table or a calculator,
We find that the z-score corresponds to 0.275 is:
= -0.63.
(b)
To find the specific number of skateboards corresponding to the z-score, we can use the formula:
x = μ + zσ
where x is the specific number of skateboards, μ is the mean (20,500), z is the z-score (-0.63), and σ is the standard deviation (55).
Substituting the values.
x = 20,500 + (-0.63) x 55
x = 20,468.35
Rounding to the nearest whole number,
x = 20,468.
Therefore,
The z-score corresponds to 0.275 is -0.63.
The specific number of skateboards corresponding to the z-score from part (a) is 20,468.
Learn more about normal distribution here:
https://brainly.com/question/31327019
#SPJ1
The eqution of the diagonal of a parallelogram is 3y=5x +k. The two opposite vertices of a parallelogram are the points (1,-2), (-2,1).Find the value of k
Answers
Answer:
\(k = 1\)
Step-by-step explanation:
Given
\(3y = 5x + k\)
Opposite points: \((1,-2)\) and \((-2,1)\)
Required
Find k
First, calculate the midpoint of the opposite points.
\((x,y) = 0.5(x_1 + x_2,y_1 + y_2)\)
This gives:
\((x,y) = 0.5(1 -2,-2 + 1)\)
\((x,y) = 0.5(-1,-1)\)
Open bracket
\((x,y) = (-0.5,-0.5)\)
The equation \(3y = 5x + k\) becomes:
\(3 * -0.5 = 5 * -0.5 + k\)
\(-1.5 = -2.5 + k\)
Solve for k
\(k = 2.5-1.5\)
\(k = 1\)
I need help with these

Answers
The 15 and 9 units side lengths of the parallelogram ABCD, and the 36° measure of the acute interior angle, A indicates the values of the ratios are;
1. AB:BC = 5:3
2. AB:CD = 1:1
3. m∠A : m∠C= 1 : 4
4. m∠B:m∠C = 4:1
5. AD: Perimeter ABCD = 3:16
What is a ratio?A ratio is a representation of the number of times one quantity is contained in another quantity.
The shape of the quadrilateral ABCD in the question = A parallelogram
Length of AB = 15
Length of BC = 9
Measure of angle m∠A = 36°
Therefore;
1. AB:BC = 15:9 = 5:3
2. AB ≅ CD (Opposite sides of a parallelogram are congruent)
AB = CD (Definition of congruency)
AB = 15, therefore, CD = 15 transitive property
AB:CD = 15:15 = 1:1
3. ∠A ≅ ∠C (Opposite interior angles of a parallelogram are congruent)
Therefore; m∠A = m∠C = 36°
∠A and ∠D are supplementary angles (Same side interior angles formed between parallel lines)
Therefore; ∠A + ∠D = 180°
36° + ∠D = 180°
∠D = 180° - 36° = 144°
∠D = 144°
m∠A : m∠C = 36°:144° =1:4
m∠A : m∠C = 1:4
4. ∠B = ∠D = 144° (properties of a parallelogram)
m∠B : m∠C = 144° : 36° = 4:1
5. AD ≅ BC (opposite sides of a parallelogram)
AD = BC = 9 (definition of congruency)
The perimeter of the parallelogram ABCD = AB + BC + CD + DA
Therefore;
Perimeter of parallelogram ABCD = 15 + 9 + 15 + 9 = 48
AD:Perimeter of the ABCD = 9 : 48 = 3 : 16
Learn more about ratios here:
https://brainly.com/question/19220252
#SPJ1
PLEASE ANSWER ASAP!
LOOK AT THE PIC ATTACHED:
(please show work!)

Answers
Explanation: Reduce the expression, if possible, by cancelling the common factors.
y2-y1/x2-x1 = ?
-20-20/30-10 = -2
a company has a policy of retiring company cars; this policy looks at number of miles driven, purpose of trips, style of car and other features. the distribution of the number of months in service for the fleet of cars is bell-shaped and has a mean of 58 months and a standard deviation of 3 months. using the empirical rule (as presented in the book), what is the approximate percentage of cars that remain in service between 61 and 64 months?
Answers
Approximately 99.7% ( or 99.73% ) population lies within 3 standard deviation ( μ - 3σ , μ + 3σ ) = ( 38, 68 ) .
Why is there a standard deviation?
The term "standard deviation" (or "") refers to the degree of dispersion of the data from the mean. Data are grouped around the mean when the standard deviation is low, and are more dispersed when the standard deviation is high.Empirical rule holds only for normal populations and states that
approximately 68% ( or 68.27%) population lies within standard deviation
( μ - σ , μ + σ ) = ( 48 , 58 )
Approximately 95% ( or 95.45% ) population lies within 2 standard deviation
( μ - 2σ , μ + 2σ ) = ( 43, 63 )
Approximately 99.7% ( or 99.73% ) population lies within 3 standard deviation
( μ - 3σ , μ + 3σ ) = ( 38, 68 )
Learn more about standard deviation
brainly.com/question/16555520
#SPJ4
Find a monthly payment on a 48 month new car loan for $15,000 with a credit score of 700Find a monthly payment on a 48 month new car loan for $15,000 with a credit score of 600
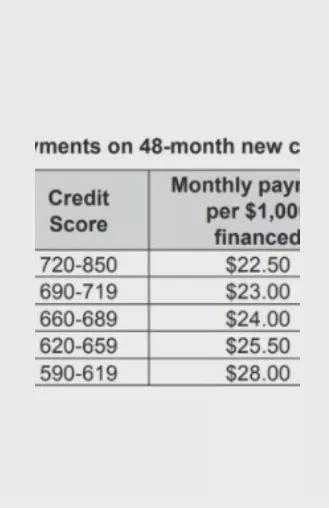
Answers
We know that with a 700 credit score we pay $23 per $1000 financed, then the monthly payment will be:
\(\frac{15000+48\cdot15\cdot23}{48}=657.50\)Therefore for a 700 credit score tour monthly payment is $657.50
Answer : $28.00
Step-by-step explanation: because it says on the chart the 590-619 it would be $28.00.
A population of measurements is approximately normal with a mean of 95 and a standard deviation of 15. The percentage of measurements that are 124. 4 or higher is.
Answers
The percentage of Measurements that are 124.4 or higher is approximately 0.99%.
In order to determine the percentage of measurements that are 124.4 or higher in a population of measurements that is approximately normal with a mean of 95 and a standard deviation of 15, we need to use the z-score formula.
The z-score formula is used to standardize a distribution so that it can be compared to a normal distribution with a mean of 0 and a standard deviation of 1.
The formula for calculating the z-score is: z = (x - μ) / σWhere:x is the measurement we want to standardize.μ is the population mean.σ is the population standard deviation.
The first step is to calculate the z-score for the measurement of 124.4:z = (124.4 - 95) / 15z = 2.2933The second step is to find the percentage of measurements that are 124.4 or higher using a standard normal distribution table. We look up the area to the right of the z-score of 2.2933 in the table.
The closest value in the table is 0.9901, which corresponds to a z-score of 2.33. We know that the area to the left of a z-score of 2.33 is 0.9901, so the area to the right of a z-score of 2.33 is:1 - 0.9901 = 0.0099
This means that approximately 0.99% of the measurements are 124.4 or higher.
Therefore, the percentage of measurements that are 124.4 or higher is approximately 0.99%.
For more quesions on Measurements .
https://brainly.com/question/27233632
#SPJ8
May currently has a balance of $1,817.43 on her credit card. if she must make a minimum monthly payment of 3.44% of her total balance, what is her minimum payment, to the nearest cent? a. $5.21 b. $62.52 c. $40.84 d. $51.49 please select the best answer from the choices provided a b c d
Answers
She makes a minimum monthly payment of 62.52 dollars. Then the correct option is B.
What is the percentage?The amount of something is expressed as if it is a part of the total which is a hundred. The ratio can be expressed as a fraction of 100. The word percent means per 100. It is represented by the symbol ‘%’.
May currently has a balance of $1,817.43 on her credit card.
If she must make a minimum monthly payment of 3.44% of her total balance.
Then the minimum payment will be given as
Minimum payment = 0.0344 × 1817.43
Minimum payment = 62.519 ≅ 62.52
More about the percentage link is given below.
https://brainly.com/question/8011401
SOMEONE PLSS HELP WITH MY ZEARN ITS 5TH GRADE MATH BTW! can be decimal or mixed number!!

Answers
Answer:
\(64 \frac{1 3}{21} ft {}^{2} \)
Step-by-step explanation:
Area of the garden:
\((8 \frac{3}{7} \times 7 \frac{2}{3} )ft {}^{2} \\ \\ ( \frac{59}{7} \times \frac{23}{ 3} )ft {}^{2} \\ \\ = \frac{1357}{21} ft {}^{2} \\ \\ = 64 \frac{13}{21} ft {}^{2} \: (ans)\)
to find the area you multiply the length by the width.
so 8 3/7 * 7 2/3
you just multiply both. so you get 64 13/21 or 64.619
Is the relation represented in this table a function?
Is the relation in this set of points a function?


Answers
Answer:
the relation in the table is a function
the relation in the set of points is not a function
Step-by-step explanation:
the definition of a function is that one input (x) can only have one output (y). In the set of points, the input 4 appears twice, which means it is not a function.
Question 3: Complex numbers (10 marks) a. Which of the following is a definition of the modulus of a complex number z? A. The real part of z.
B. The distance between z and the origin in the Argand plane. C. The result of turning each imaginary part of a negative. D. The angle between the x-axis and the line from the origin to z. (1 mark)
Answers
The modulus of a complex number is defined as the distance between the complex number and the origin in the Argand plane.
The correct definition of the modulus of a complex number is option B: the distance between the complex number, denoted as z, and the origin in the Argand plane. The Argand plane is a two-dimensional plane where the real part of the complex number is represented on the x-axis, and the imaginary part is represented on the y-axis. In this plane, the complex number z is represented as a point with coordinates (a, b), where 'a' is the real part and 'b' is the imaginary part.
The modulus of z, denoted as |z|, can be calculated using the distance formula from Euclidean geometry. It is given by the square root of the sum of the squares of the real and imaginary parts of z. Mathematically, |z| = √(a^2 + b^2). This modulus represents the length of the line segment connecting the origin to the point (a, b) in the Argand plane.
In summary, the modulus of a complex number is defined as the distance between the complex number and the origin in the Argand plane. It is calculated using the square root of the sum of the squares of the real and imaginary parts of the complex number.
Learn more about Argand plane here:
https://brainly.com/question/31973424
#SPJ11
a couple decided to have 4 children. (a) what is the probability that they will have at least one girl? (b) what is the probability that all the children will be of the same gender?
Answers
(a) The probability of having at least one girl is 1 - 0.0625 = 0.9375 or 93.75%.
(b) The probability that all the children will be of the same gender is 0.0625 + 0.0625 = 0.125 or 12.5%.
The probability of having at least one girl can be calculated by finding the probability of having no girls and subtracting it from 1.
Assuming that the probability of having a boy or a girl is equal (0.5), the probability of having no girls is (0.5)^4 = 0.0625.
Therefore, the probability of having at least one girl is 1 - 0.0625 = 0.9375 or 93.75%.
(b) The probability that all the children will be of the same gender is 0.0625 + 0.0625 = 0.125 or 12.5%.
The probability that all the children will be of the same gender can be calculated by finding the probability of having all boys and adding it to the probability of having all girls.
The probability of having all boys is (0.5)^4 = 0.0625, and the probability of having all girls is also 0.0625.
Therefore, the probability that all the children will be of the same gender is 0.0625 + 0.0625 = 0.125 or 12.5%.
Learn more about Probability:
https://brainly.com/question/13604758
#SPJ1
help me please??????

Answers
Answer:
Step-by-step explanation:
what is the slope of the line parallel to the line whose equation is -y = -4x + 7 ?
Answers
-y = -4x + 7
Solve for y
y = 4x - 7
Since the line is parallel to this one, they would have the same slope.
Hello there!
Parallel lines have the same slope.
So if one line has a slope of 4, then the slope of the line parallel to it has a slope of 4 as well.
Hope it helps!
Please mark Brainliest!
~Just a determined gal
\(MysteriousNature\) here to help
Christina is packing different books into boxes. The paperback booksweigh 0.8 pounds each. The hardcover books weigh 1.3 pounds each.Christina needs to pack the boxes so there are at least 20 books in each box, but the boxes cannot weigh more than 30 pounds. If x represents thenumber of paperback books, and y represents the number of hardcoverbooks, identify Christina's set of constraints (Check all that apply).

Answers
Step 1. Identify the variables.
\(\begin{gathered} x\longrightarrow\text{ Number of }paperback\text{ books} \\ y\longrightarrow\text{Number of }hardcover\text{ books} \end{gathered}\)Step 2. Find the first constraint using the condition for the total number of books in each box.
The problem states "Christina needs to pack the boxes so there are at least 20 books in each box" This means that the sum of x and y must be at least 20, this is represented in the following inequality:
\(x+y\ge20\)That is the first constraint.
Step 3. Find the second constraint using the condition for the weight of each box.
The problem states: "the boxes cannot weigh more than 30 pounds" and since the paperback books weigh 0.8 pounds and the hardcover books weigh 1.3 pounds each, the sum of their weights is:
\(0.8x+1.3y\)This sum cannot be more than 30, which is represented by the following inequality:
\(0.8x+1.3y\leq30\)Answer:
The set of constraints is
\(\begin{gathered} x+y\ge20 \\ 0.8x+1.3y\leq30 \end{gathered}\)
A summer camp basketball coach is hired to work 10 hours per week. During a really busy first week, they were required to work 15 hours. What percentage of time did they work during the busy week? Show your work.
Answers
Answer:
150%
Step-by-step explanation:
15 / 10 =
1.5 =
150%
Evaluate the expression
a:1/2
5a
Answers
Answer:
5a^2/2
Step-by-step explanation:
Answer: 3.2
Step-by-step explanation:
1/2 a = 5a
f(x) = x ^ 2 + 5x + 6

Answers
b)-294
this is the answer to the two questions on the provided picture
the probability that a married couple pays for their honeymoon is 0.56. you randomly select 5 couples and ask each if they paid for their honeymoon themselves. find the probability that exactly 4 of the couples said that they paid for their honeymoon.
Answers
0.2164 is probability that exactly 4 of the couples said that they paid for their honeymoon.
What are examples and probability?
It is based on the probabilities that something could happen. The logic underpinning probability serves as the foundation for theoretical probability. The theoretical likelihood of receiving a head, for instance, is 12 when a coin is tossed.If x = no of married couples out of 5 who paid for their honeymoon .
then X ~ ( 5 , 0.56 )
P (X = 4 ) = 5C4( 0.56 )⁴ ( 0.44)¹
= 0.2164
Learn more about probability
brainly.com/question/11234923
#SPJ4
In what direction is the derivative of f(x,y) = xy + y2 at P(4,9) equal to zero?
Answers
In what direction is the derivative of f(x,y) = xy + y2 at P(4,9) equal to zero
then, the value is (5,22).
Directional Derivative:
The directional derivative of a function
\(D_u\) f(x, y) at a point (x0,y0) in the direction of the unit vector \(u^{-}\), denoted
f(x0,y0), can be calculated by first evaluating the gradient of f at this
point :
∇f(x₀, y₀) = ⟨∂f/∂x(x₀, y₀),∂f/∂y (x₀, y₀)⟩
and then computing the dot product of this with the given unit vector:
\(D_u\) f(x₀, y₀) = ∇f(x₀, y₀) × \(u^{-}\)
If the directional derivative of a function at a point is zero in some direction, then the unit vector must be perpendicular to the gradient at that point.
Given that:
f(x, y) = xy + y² at P(4,9)
Now,
f(x, y) = xy + y²
⇒ fₓ = δ/δₓ f(x, y)
= y
And,
(fₓ)₍₅,₉₎ = 4
\(δ_y\) = \(δ\)/\(δ_y\) f(x, y)
= (x + 2y)
= 4 + 2× 9
= 22
Therefore,
Δf₍₅,₉₎ = { y, x+2y}
= {4,22}
Learn more about Derivative:
https://brainly.com/question/25324584
#SPJ4
Will Mark brainliest if answer both correctly / What is X= ? / conditional statement

Answers
Explanation:
For the 1st question:
tan = opposite / adjacent
tan 30 = x / 18
18 tan 30 = x
x = 10.4
For the 2nd question,
If a triangle as an angle of 90 degree, it is 100% a right triangle.
Hope it helps :), mark me brainliest please!
20,000 people voted in each county, and there
are 7 counties. What is the order of magnitude
for the total number of people who voted?
Answers
Answer:
5
Step-by-step explanation:
20000*7=140,000
1.4 * 10 to the 5 power,
So its order of magnitude is 5.
Write the following expressions in a more compact way (i.e.,
using index i, j as above).
c1x1 + c2x2 + c3x3 = 40
Answers
Using index notation, the expression can be written more compactly as:
∑(c_ix_i) = 40
How to explain the notationIn the given expression, we have three terms: \(c_{1}\)\(x_{1}\), \(c_{1}\)\(x_{2}\), and \(c_{3}\)\(x_{3}\). Each term represents the product of a coefficient (c₁, c₂, or c₃) and a variable (x₁, x₂, or x₃). The sum of these three terms equals 40.
In order to write this expression using index notation, we introduce the index i to represent the three variables. We can rewrite the terms as c_ix_i, where i takes the values 1, 2, and 3.
The notation ∑(c_ix_i) represents the sum of all terms c_ix_i over the range of i. In this case, it represents the sum of \(c_{1}\)x₁, \(c_{2}\)\(x_{2}\), and \(c_{3}\)\(x_{3}\).
Learn more about notation on
https://brainly.com/question/1767229
#SPJ4
Barney just bought stock in Purple Dinosaur Industries. He paid a total of $7,380. The price of the stock is $12 for one share. How many shares did he buy?
Answers
The number of shares he buy is $615.
Given that Barney just bought stock in Purple Dinosaur Industries and he paid a total of $7,380 and the price of the stock is $12 for one share.
We want to find the number of shares Barney buys.
The total amount barney should pay is $7380.
The price of the stock for one share is $12.
The total number of shares barney buy is 7380/12=615.
Hence, the number of shares barney should buy when he paid a total $7380 and the price of stock for one share is $12 is $615.
Learn more about the word problem from here brainly.com/question/25693822
#SPJ9
A
company expects to receive $40,000 in 10 years time. What is the
value of this $40,000 in today's dollars if the annual discount
rate is 8%?
Answers
The value of $40,000 in today's dollars, considering an annual discount rate of 8% and a time period of 10 years, is approximately $21,589.
To calculate the present value of $40,000 in 10 years with an annual discount rate of 8%, we can use the formula for present value:
Present Value = Future Value / (1 + Discount Rate)^Number of Periods
In this case, the future value is $40,000, the discount rate is 8%, and the number of periods is 10 years. Plugging in these values into the formula, we get:
Present Value = $40,000 / (1 + 0.08)^10
Present Value = $40,000 / (1.08)^10
Present Value ≈ $21,589
This means that the value of $40,000 in today's dollars, taking into account the time value of money and the discount rate, is approximately $21,589. This is because the discount rate of 8% accounts for the decrease in the value of money over time due to factors such as inflation and the opportunity cost of investing the money elsewhere.
Learn more about discount
brainly.com/question/13501493
#SPJ11