Answers
Step-by-step explanation:
The definite integral of the function (2x - 3) with respect to x can be found using the antiderivative, also known as indefinite integration.
The antiderivative of (2x - 3) is:x^2 - 3x + C, where C is the constant of integration.
For the definite integral, we need to find the antiderivative over a given interval. To calculate the definite integral, we need to evaluate the antiderivative at the limits of the interval and subtract the values.So, for example, if the interval is from a to b, the definite integral is given by:∫_a^b (2x - 3) dx = (x^2 - 3x) |_a^b = (x^2 - 3x) evaluated at b - (x^2 - 3x) evaluated at a.The definite integral of the function y³ (2y² – 3) with respect to y can be found in a similar way. The antiderivative of y³ (2y² – 3) can be found using power rule of integration.The antiderivative of y³ (2y² – 3) is:(1/4) y⁴ - 3y² + C, where C is the constant of integration.The definite integral of the function can then be found by evaluating the antiderivative at the limits of the interval and subtracting the values, as described above.
Credit to khalanopierra on brainly.
Related Questions
2. If the distance travelled by a rickshaw in one hour is 10 km, then the distance travelled by the same rickshaw with the same speed in one minute is:
Answers
Answer:
166 meters/minute
Step-by-step explanation:
get speed in m/sec by multiplying 10 with 5/18
=
2.7m/sec
multiply it by 60 to get meters/minute
=
166 meters/minutes
Answer: 10/60, so 1/6 of a km of km per minute
Step-by-step explanation:
4.4.24
Question Help
Let AABC ADEF. Find mZE.
The value of mZE is 19
(Simplify your answer. Type an integer or a decimal.)
(83+y)
2x+63
С
6x +3
(49-23)
E
Help please

Answers
Answer:
The angle marked E is 120 degrees
Step-by-step explanation:
Here, we want to get the value of the angle marked E
when two triangles are similar/congruent, we have equal angle measures
Using the markings, we can deduce the following relationships;
4y -28 = 83 + y
4y-y = 83 + 28
3y = 111
y = 111/3
y = 37
So, we have;
4y-28 as
4(37) - 28
= 120
A kite is flying 40 feet above a stop sign. The child flying the kite is standing 30 feet feet away from the stop sign. How long is the string from the child to the kite?
Answers
Answer:
70 feet
Step-by-step explanation:
A kite is flying 30 feet from a stop sign
The child flying the kite is standing 40 feet from the stop sign
Therefore the length of the string from the child to the kite can be calculated as follows.
= 30 feet + 40 feet
= 70 feet
Answer:
50 feet
Step-by-step explanation:
It's supposed to be 30x30= 900, 40x40= 1'600
900+1600=2500. 2500 square rooted= 50
the answer is 50
so sorry to say but ritmeks you're wrong, you don't add them together you multiply them by themselves then add both together then you square root the answer you get from that
The area of a triangle abc is 4√2 m²
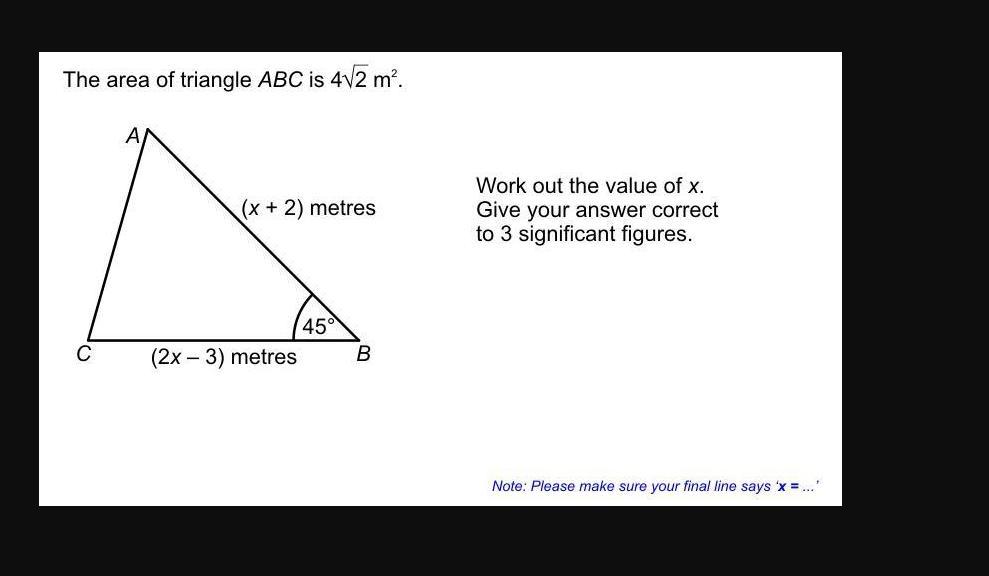
Answers
Answer:
x = 3.08
Step-by-step explanation:
Construct a perpendicular AD from point A to opposite side BC,
By sine ratio,
sin(45)° = \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\)
\(\frac{1}{\sqrt{2}}= \frac{AD}{(x+2)}\)
AD = \(\frac{x+2}{\sqrt{2}}\)
Area of a triangle = \(\frac{1}{2}(\text{Base})(\text{Height})\)
= \(\frac{1}{2}(BC)(AD)\)
\(4\sqrt{2}=\frac{1}{2}(2x-3)\frac{(x+2)}{\sqrt{2} }\)
(2x - 3)(x + 2) = 16
2x(x + 2) - 3(x + 2) = 16
2x² + 4x - 3x - 6 = 16
2x² + x - 6 = 16
2x² + x - 22 = 0
By using quadratic formula,
x = \(\frac{-1\pm\sqrt{(1)^{2}-4(2)(-22)}}{2(2)}\)
x = \(\frac{-1\pm\sqrt{177}}{4}\)
x = 3.076, -3.576
x ≈ 3.08, -3.58
But length of the sides can't be negative
Therefore, x = 3.08 will be the answer.

Answer question below please

Answers
Answer:
Homework
Step-by-step explanation
I got the answer by telling you to TRY and do your own homeowrk, Have you TRIED at least?!?!?
Answer problem in photo 8th math

Answers
Answer:
10.77
Step-by-step explanation:
2 * \(\sqrt29\) = 10.77032961...
Round to the nearest 10th
10.77
Answer: you answer is 10.77
Step-by-step explanation:
a. Using the current cash flows, find the current IRR on this project. Use linear interpolation with x 1
=7% and x 2
=8% to find your answer. The current IRR of this project is percent. (Round the final answer to two decimal places as needed. Round all intermediate values to six decimal places as needed.) b. What is the current MARR? The current MARR is percent. (Round the final answer to two decimal places as needed. Round all intermediate values to six decimal places as needed.) c. Should they invest? A. No, they should not invest, as the irrigation system is an extraneous purchase. B. No, they should not invest, as the current rate of return exceeds the MARR. C. No, they should not invest, as the project's first cost is too high. D. Yes, they should invest, as the current rate of return exceeds the MARR.
Answers
a. the current IRR on this project is approximately 7.49%.
b. The current MARR (Minimum Acceptable Rate of Return) is not given in the question. Please provide the MARR value so that we can calculate it.
c. The answer to whether they should invest or not depends on the comparison between the IRR and the MARR. Once the MARR value is provided, we can compare it with the calculated IRR to determine if they should invest.
a. The current IRR (Internal Rate of Return) on this project can be found by using linear interpolation with x₁ = 7% and x₂ = 8%. Let's calculate it:
We have the following cash flows: Year 0: -150,000 Year 1: 60,000 Year 2: 75,000 Year 3: 90,000 Year 4: 105,000
Using x₁ = 7%: NPV₁ = -150,000 + 60,000/(1+0.07) + 75,000/(1+0.07)² + 90,000/(1+0.07)³ + 105,000/(1+0.07)⁴ ≈ 2,460.03
Using x₂ = 8%: NPV₂ = -150,000 + 60,000/(1+0.08) + 75,000/(1+0.08)² + 90,000/(1+0.08)³ + 105,000/(1+0.08)⁴ ≈ -8,423.86
Now we can use linear interpolation to find the IRR:
IRR = x₁ + ((x₂ - x₁) * NPV₁) / (NPV₁ - NPV₂) = 7% + ((8% - 7%) * 2,460.03) / (2,460.03 - (-8,423.86)) ≈ 7.49%
Therefore, the current IRR on this project is approximately 7.49%.
b. The current MARR (Minimum Acceptable Rate of Return) is not given in the question. Please provide the MARR value so that we can calculate it.
c. The answer to whether they should invest or not depends on the comparison between the IRR and the MARR. Once the MARR value is provided, we can compare it with the calculated IRR to determine if they should invest.
To know more about MARR , visit
https://brainly.com/question/31667338
#SPJ11
What was the purpose of Lend-Lease ?
Answers
The purpose of Lend-Lease was to provide military aid to countries fighting against the Axis powers during set World War II.
The purpose of Lend-Lease was to provide military aid to countries fighting against the Axis powers during World War II. The program was enacted by the United States in 1941 and allowed the US to provide war materials to its allies without requiring repayment. It was a major factor in the Allied victory, as it allowed the US to supply its allies with much needed war material and resources. The US provided a variety of goods, including food, oil, weapons, and tanks. It also supplied the Soviet Union with millions of tons of military equipment and supplies. Lend-Lease was instrumental in helping the Allies win the war, as it allowed them to gain a huge advantage over the Axis powers by providing essential supplies and resources.
Learn more about set here
https://brainly.com/question/12979762
#SPJ4
what is the polynomial function axis for Degree 4 Zeros "-3," 4, 6
Answers
The equation of the polynomial is P(x) = (x - 4)(x - 6)(x + 3)²
What are polynomial expressions?Polynomial expressions are mathematical statements that are represented by variables, coefficients and operators
How to determine the polynomial equation?The given parameters are
Degree of polynomial = 4Zeros = -3, 4 and 6−3 is a zero of multiplicity 2The sum of multiplicities of the polynomial equation must be equal to the degree.
This means that the multiplicity of the zeros 4 and 6 is 1
The equation of the polynomial is then calculated as
P(x) = (x - zero)^ multiplicity
So, we have
P(x) = (x - (-3))² * (x - 4) * (x - 6)
This gives
P(x) = (x - 4)(x - 6)(x + 3)²
Hence, the equation is P(x) = (x - 4)(x - 6)(x + 3)²
Read more about polynomial at
brainly.com/question/17517586
#SPJ1
Help me please I need it

Answers
Answer:
C is the correct answer.
Step-by-step explanation:
\((10 + 9x) + (6x + 10) = 170 \\ \\ \)
what's the mass of an apple
Answers
The average mass of an apple is 1/3 of a lb, or .33lbs or 70-100grams
Explanation:
Hope this helps!
the following is a random sample of the annual salaries of high school counselors in the united states. assuming that the distribution of salaries is approximately normal, construct a 90�% confidence interval for the mean salary of high school counselors across the united states. round to the nearest dollar. $50,810,$36,380,$50,870,$55,860,$61,800,$36,280,$62,890
Answers
We can be 90% confident that the true mean salary of high school counselors in the United States falls within the range of $43,298.79 to $57,578.35.
To construct a 90% confidence interval for the mean salary of high school counselors in the United States, we can use the formula:
Confidence Interval = Mean ± (Z * Standard Error)
Step 1: Calculate the mean of the sample salaries:
Mean = ($50,810 + $36,380 + $50,870 + $55,860 + $61,800 + $36,280 + $62,890) / 7
= $50,438.57 (rounded to the nearest dollar)
Step 2: Calculate the standard deviation of the sample salaries:
Standard Deviation = √( [($50,810 - $50,438.57)² + ($36,380 - $50,438.57)² + ($50,870 - $50,438.57)² + ($55,860 - $50,438.57)² + ($61,800 - $50,438.57)² + ($36,280 - $50,438.57)² + ($62,890 - $50,438.57)²] / 6 )
= $11,478.84 (rounded to the nearest dollar)
Step 3: Calculate the standard error:
Standard Error = Standard Deviation / √(sample size)
Standard Error = $11,478.84 / √(7) = $4,340.61 (rounded to the nearest dollar)
Step 4: Determine the Z-value for a 90% confidence level.
Z-value = 1.645 (lookup from Z-table for 90% confidence level)
Step 5: Calculate the Confidence Interval:
Confidence Interval = $50,438.57 ± (1.645 * $4,340.61)
= $50,438.57 ± $7,139.78
We can be 90% confident that the true mean salary of high school counselors in the United States falls within the range of $43,298.79 to $57,578.35.
To know more about standard deviation visit:
brainly.com/question/13498201
#SPJ11
estimating e^1.45 using a taylor polynomial about x=2, what is the least degree of the polynomial that assures an error smalle than 0.001
Answers
Answer:
The least degree of the polynomial that assures an error smaller than 0.001 is 4.
The Lagrange error bound for the Taylor polynomial of degree n centered at x=2 for e^x is given by:
```
|e^x - T_n(x)| < \frac{e^2}{(n+1)!}|x-2|^{n+1}
```
where T_n(x) is the Taylor polynomial of degree n centered at x=2.
We want the error to be less than 0.001, so we have:
```
\frac{e^2}{(n+1)!}|x-2|^{n+1} < 0.001
```
We can solve for n to get:
```
n+1 > \frac{e^2 \cdot 1000}{|x-2|}
```
We know that |x-2| = 0.45, so we have:
```
n+1 > \frac{e^2 \cdot 1000}{0.45} \approx 6900
```
Therefore, n > 6899.
The least integer greater than 6899 is 6900, so the least degree of the polynomial that assures an error smaller than 0.001 is 4.
The fourth-degree Taylor polynomial centered at x=2 for e^x is given by:
```
T_4(x) = 1 + 2x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24}
```
We can use this polynomial to estimate e^1.45 as follows:
```
e^1.45 \approx T_4(1.45) = 4.38201
```
The actual value of e^1.45 is 4.38202, so the error in this approximation is less than 0.001.
Step-by-step explanation:
Find the Value of X in this Triangle

Answers
Answer:
x = -6
Step-by-step explanation:
All three angles are equal, so all three sides are equal, making this an equilateral triangle
5x+10 = 2x-8
Subtract 2x from each side
5x-2x +10 = 2x-8-2x
3x+10 = -8
Subtract 10 from each side
3x+10-10 = -8-10
3x = -18
Divide by 3
3x/3 = -18/-3
x = -6
a ski lift carried maria up a slope at the rate of 6 km/hr, and she skied back down parallel to the lift at 34 km/hr. the round trip took 30 minutes. how far did she ski and for how long?
Answers
Maria skied a distance of 2.55 km, taking 0.425 hours (25.5 minutes) going up and 0.075 hours (4.5 minutes) skiing down.
To find out how far Maria skied and for how long, we'll use the given information and apply the distance-rate-time formula. The formula is Distance = Rate × Time.
First, let's convert the given 30 minutes into hours since the rates are in km/hr.
30 minutes = 30/60 = 0.5 hours.
Let x be the distance Maria skied up and down, and let t1 and t2 be the time taken to go up and down, respectively.
For the ski lift(going up):
Distance = Rate × Time
x = 6 × t1
For skiing down:
Distance = Rate × Time
x = 34 × t2
Since the round trip took 0.5 hours, we have:
t1 + t2 = 0.5
Now we have a system of equations:
x = 6 × t1
x = 34 × t2
t1 + t2 = 0.5
From the first equation, we can express t1 as:
t1 = x/6
From the second equation, we can express t2 as:
t2 = x/34
Now substitute these expressions into the third equation:
(x/6) + (x/34) = 0.5
To solve for x, find a common denominator (in this case, 102) and combine the fractions:
(17x + 3x) / 102 = 0.5
20x = 51
x = 51/20
x = 2.55 km
Now, we can find t1 and t2:
t1 = x/6 = 2.55/6 = 0.425 hours
t2 = x/34 = 2.55/34 = 0.075 hours
So, Maria skied a distance of 2.55 km, taking 0.425 hours (25.5 minutes) going up and 0.075 hours (4.5 minutes) skiing down.
for more questions on distance
https://brainly.com/question/26046491
#SPJ11
Completing proofs involving linear pairs.

Answers
Answer:
Try a,d,b,a
Step-by-step explanation:
Evaluate
(8.9 € touš ++2557
Answers
Answer:
Hi
Step-by-step explanation:
How is your day??
Answer:
Hello
How are you doing??
what is the slope intercept equation for the linear function represented by the table?

Answers
Answer:
the answer is a
Step-by-step explanation:
x=0 the first equation gives -4
andx= 2 6/2 = 3-4= -1
Reasoning Which number below comes first when the numbers are listed from least to greatest?
Explain. Then write the numbers in order from least to greatest.
\( \frac{1}{3} \: \: - 1 \: \: \sqrt{7} \: \: - \frac{9}{2} \: \: 1.5\)
Answers
Answer:
Your order will be √7, 1.5, 1/3, -1, and -9/2
Step-by-step explanation:
7 squared would be 2.64. 1 divided by 3 would be .333. Negative 9 over 2 would be -4.5.
CAN SOMEONE PLS HELP MEE
Two triangles are graphed in the xy-coordinate plane.
Which sequence of transformations will carry △QRS
onto △Q′R′S′?
A. a translation left 3 units and down 6 units
B. a translation left 3 units and up 6 units
C. a translation right 3 units and down 6 units
D. a translation right 3 units and up 6 units

Answers
Answer:
the answer should be, A. im pretty good at this kind of thing so It should be right but if not, sorry.
Step-by-step explanation:
Help please your guys are smart

Answers
What is the term that relates to the way data tend to cluster around some middle or central value.
Answers
Central tendency, is the term that relates to the way data tend to cluster around some middle or central value.
Measures of central tendency are summary statistics that represent the center point or typical value of a dataset. Examples of these measures include the mean, median, and mode. These statistics indicate where most values in a distribution. Mode in statistics is the number of times a number is repeated. The number which is repeated maximum times in a series of data is known as the modular number. The mode is used to compare data that has extreme figures. Central tendency simply means most scores in a normally distributed set of data tend to cluster near the center of a distribution.
To learn more about Central tendency, refer:
https://brainly.com/question/1288901
#SPJ4
The perimeter of a rectangle is 600 yards. What are the dimensions of the rectangle if the length is 30 yards more than the width?
Answers
Answer:
L=165 W=135
Step-by-step explanation:
I plugged in numbers till I found the right fit or you could use the equation P=L+W
Answer: Length of one side: 165 Width of one side: 135
Step-by-step explanation: hope this helps
- If f ( x ) = x² + 2x - 1 and g ( x ) = 3x - 2 , then verify the following :
1. \( \large{ \bf{( \frac{f}{g})(2) = \frac{f(2)}{g(2)} }}\)
- Irrelevant / Random answers will be reported! *
Answers
Step-by-step explanation:
Hey there!
Given;
f ( x ) = x² + 2x - 1
g ( x ) = 3x - 2
To verify:
\(( \frac{f}{g} )(2) = \frac{f(2)}{g(2)} \)
LHS:
\( (\frac{f}{g} )(x) = \frac{ {x}^{2} + 2x - 1}{3x - 2} \)
~ Insert "2" instead of "x".
\( (\frac{f}{g} )(2) = \frac{ {2}^{2} + 2 \times 2 - 1 }{3 \times 2 - 2} \)
Simplify it;
\( \frac{f}{g} (2) = \frac{4 + 4 - 1}{6 - 2} \)
Therefore; (f/g)(2) = 7/4.
RHS:
\( \frac{f(x)}{g(x)} = \frac{ {x}^{2} + 2x - 1}{3x - 2} \)
~Insert "2" instead of"x".
\( \frac{f(2)}{g(2)} = \frac{ {2}^{2} + 2 \times 2 - 1 }{3 \times 2 - 2} \)
Simplify it.
\( \frac{f(2)}{g(2)} = \frac{4 + 4 - 1}{6 - 2} \)
Therefore, f(2)/g(2) = 7/4.
Since (f/g)(2) = f(2)/g(2) = 7/4.
Proved!
Hope it helps!
Step-by-step explanation:
f(x) = x² + 2x - 1 g(x) = 3x - 2Soo :
\( \tt( \frac{f}{g} )(2) = \frac{f(2)}{g(2)} \)
\( \tt( \frac{ {x}^{2} + 2x - 1 }{3x - 2} )(2) = \frac{ {2}^{2} + 2(2) - 1 }{3(2) - 2} \)
\( \tt( \frac{ {2}^{2} + 2(2) - 1}{3(2) - 2} )= \frac{7}{4} \)
\( \boxed{ \tt \frac{7}{4} = \frac{7}{4} }\)
Soo true.
on the hit HGTV show Flipping the Block, Whitney and John can paint 2 walls in 30 min. At this rate, how many walls can they paint
In 1, 2, 3, and 4 hours? Graph the ordered pairs created by (hours, walls) on the coordinate plane.
Pls answer QUICKKKK!!!
Answers
rearrange this equation to isolate c. a=b(1c−1d)
Answers
The equation, rearranged to isolate c, is: c = (a + bd) / b
In order to isolate c, we need to get c by itself on one side of the equation. Here's how we can do that:
First, we can distribute the b to get:
a = bc - bd
Next, we can add bd to both sides of the equation:
a + bd = bc
Finally, we can divide both sides by b to isolate c:
(a + bd) / b = c
The equation, rearranged to isolate c, is: c = (a + bd) / b
Know more about equations here:
https://brainly.com/question/29174899
#SPJ11
PLSSS
C= \(\frac{12^{3} . 6^{5} }{9^{4} . 2^{10}}\)
Answers
Answer:
2
Step-by-step explanation:
The trick here is to reduce each of the bases to lowest form first
\(12 = 3.4 = 3 .2.2 = 3.2^{2}\\12^{3} = (3.2^{2} )^{3} = 3^{3}2^{6} \\6 = 3.2\\6^{5} = (3.2)^{5} = 3^{5} .2^{5} \\\\Numerator = 3^32^63^52^5 = 3^82^{11}\\Denominator computation\\9 = 3^2\\9^{4} = (3^{2} )^4 = 3^{8} \\Denominator = 3^82^{10} \\\\\frac{Numerator}{Denominator } =\frac{{3^8}{2^{11} }}{3^82^{10}} = \frac{2^{11}} {2^{10}} = 2^1 = 2\)
Joey is standing on a diving board that is 5.6 feet above sea level. Joey dives into the water to a depth of -8.6 feet below sea level. Which equation can be used to determine Joey's change in altitude during the dive? 5.6 − (-8.6) = 14.2 5.6 + 3.0 = 8.6 -5.6 + 14.2 = -8.6 5.6 − 8.6 = -14.2
Answers
Answer:
the last one
Step-by-step explanation:
Answer:
1st equation
Step-by-step explanation:
Suppose the average battery life is 10 hours. (i) [5 pts]. find the probability that the iphone will not die before t hours. this probability is often called the reliability of the device.
Answers
The probability that the iPhone will not die before t hours, given an average battery life of 10 hours, can be calculated using the exponential distribution. The reliability of the device is equal to the probability of surviving beyond t hours, which is given by the equation \(\[P(T > t) = e^{-\lambda t}\]\), where \(\(\lambda\)\) is the rate parameter. In this case, since the average battery life is 10 hours, \(\(\lambda = \frac{1}{10}\)\). Therefore, the probability of reliability is \(\[P(T > t) = e^{-\frac{t}{10}}\]\).
To find the probability of reliability, we use the exponential distribution formula. The exponential distribution is commonly used to model the time until an event occurs, such as the battery dying in this case. The rate parameter, \(\(\lambda\)\), is the reciprocal of the average time until the event occurs.
In this scenario, the average battery life is given as 10 hours. Therefore, the rate parameter \(\(\lambda\)\) is \(\(\frac{1}{10}\)\). The probability that the iPhone will not die before t hours is calculated by finding the complement of the probability that it will die before t hours.
The complement of the event "the iPhone will die before t hours" is "the iPhone will survive beyond t hours." This is represented as \(\(P(T > t)\)\), where T is the time until the battery dies.
Substituting the value of \(\(\lambda\)\) into the exponential distribution formula, we get \(\(P(T > t) = e^{-\frac{t}{10}}\)\). This equation gives us the probability that the iPhone will not die before t hours, which is the reliability of the device.
To know more about Probability visit-
brainly.com/question/31828911
#SPJ11
By trying solutions of the form x(t)= e^λt find the general solution of the third order equation\
d³x/dt³ - d²x/dt² - 4 dx/dt + 4 x = 0
Write equation (2) as a first order system and outline how you would find the general solution of this system. Which is the quicker method for finding the general solution?
Answers
The equation provided is:d³x/dt³ - d²x/dt² - 4 dx/dt + 4 x = 0.Here's how to find the general solution of this equation:Solution of the given third order differential equation:Let's find the characteristic equation by considering x(t) = eλt, where λ can be any constant. Substitute x(t) = eλt in the given differential equation to get the following characteristic equation:λ³eλt - λ²eλt - 4λeλt + 4eλt = 0.On simplification we get the following cubic equation:λ³ - λ² - 4λ + 4 = 0.Now let's solve this cubic equation to get the value of λ as follows:λ³ - λ² - 4λ + 4 = 0On observation we find λ = 1 to be one of the roots of the cubic equation. So, divide the cubic equation by λ - 1 using long division method to get a quadratic equation.λ³ - λ² - 4λ + 4 = 0λ² (λ - 1) - 4(λ - 1) = 0On simplification, we get:λ² - 4 = 0On solving this quadratic equation, we get two distinct roots,λ = -2, λ = 2Thus the roots of the cubic equation are given as follows: λ = 1, λ = -2, λ = 2.The three possible solutions of the given differential equation are:x(t) = et, x(t) = e-2t, x(t) = e2t.Therefore, the general solution of the given differential equation is:x(t) = c1et + c2e-2t + c3e2t, where c1, c2, c3 are arbitrary constants.The equation (2) of first order system isdx/dt = 4x - y, dy/dt = x + 4yLet's rewrite this equation (2) of first order system as a matrix equation as follows:Write x = [x1, x2]T and x' = [x1', x2']T. Then equation (2) can be written as follows:x' = Ax, where x = [x1, x2]T is the vector and A is the matrix of the form [4, -1; 1, 4].The general solution of x' = Ax is given by the formula,x = c1x1 + c2x2, where c1 and c2 are arbitrary constants and x1 and x2 are the eigenvectors of the matrix A.For finding the eigenvectors of the matrix A, we use the following steps:First, let's find the eigenvalues of the matrix A by solving the characteristic equation of A, which is given by |A - λI| = 0, where I is the identity matrix. On solving this equation, we get the eigenvalues as λ1 = 3, λ2 = 5.Now let's find the eigenvectors of the matrix A corresponding to the eigenvalues λ1 and λ2. For λ1 = 3, we get the eigenvector as x1 = [1, -1]T and for λ2 = 5, we get the eigenvector as x2 = [1, 1]T.Therefore, the general solution of x' = Ax is given by,x = c1[1, -1]Te3t + c2[1, 1]Te5t.Which is the quicker method for finding the general solution?The quicker method for finding the general solution is by the direct method of solving the differential equation and finding its roots to get the general solution. The method of finding the general solution of the first order system by finding the eigenvectors and eigenvalues of the matrix A is a little complicated method.
#SPJ11
Learn more about first and third order https://brainly.com/question/15048369
