Lacy ha 10 gallon of water. She pour an equal number of gallon of water into each of 3 fih tank. Lacy' blue fih tank already ha 1 third gallon of water in it. How many gallon of water doe lacy blue fih tank ha now? fi
Answers
Lacy's blue fish tank has now 3 2/3 gallons of water.
If Lacy has 10 gallons of water and she pour an equal number of gallons of water into each of her 3 fish tanks, then the amount of water each tank will have is equal to the quotient of 10 divided by 3.
amount of water poured in each tank = 10 gallons / 3
amount of water poured in each tank = 10/3 gallons
If Lacy's blue fish tank already has 1/3 gallon of water in it, then the total amount of water the blue fish tank has is the sum of the two fractions.
Add the initial amount and the amount poured in after.
1/3 + 10/3 = 11/3 = 3 2/3 gallons
Simplifying the fraction, Lacy's blue fish tank has now 3 2/3 gallons of water.
Learn more about fraction here: brainly.com/question/729654
#SPJ4
Related Questions
What is the most important characteristic of a correlation coefficient?
a. number of variables included
b. absolute value
c. one tailed
d. two tailed
Answers
Answer:
The most important characteristic of a correlation coefficient is the absolute value.
The absolute value of a correlation coefficient represents the strength of the relationship between two variables, regardless of the direction of the relationship. A correlation coefficient can range from -1 to +1, where a value of -1 indicates a perfect negative correlation (i.e., as one variable increases, the other decreases), a value of +1 indicates a perfect positive correlation (i.e., as one variable increases, the other also increases), and a value of 0 indicates no correlation (i.e., there is no relationship between the variables).
The most important characteristic of a correlation coefficient is the absolute value.
The absolute value of the correlation coefficient represents the strength of the relationship between two variables, regardless of its direction. It indicates the degree to which the variables are associated with each other.
By focusing on the absolute value, we can assess the magnitude of the correlation without being influenced by whether it is positive or negative. For example, a correlation coefficient of -0.8 or +0.8 both indicate a strong relationship, while a correlation coefficient of 0 suggests no relationship.
The number of variables included is not a characteristic of the correlation coefficient itself, but rather a consideration in the analysis. One-tailed and two-tailed refer to the type of hypothesis being tested and are relevant in statistical testing. However, the absolute value of the correlation coefficient is crucial in determining the strength of the relationship between variables, making it the most important characteristic to assess in correlation analysis.
To know more about correlation coefficient refer here:
https://brainly.com/question/29704223
#SPJ11
(3 2 Find the general solution of the homogeneous system. X'= X -
Answers
The general solution of the homogeneous system X' = AX is given by X(t) = ce^(At), where A is the coefficient matrix, X(t) is the vector of unknowns, and c is a constant vector.
To find the general solution of the homogeneous system X' = X, we need to determine the coefficient matrix A. In this case, the coefficient matrix is simply A = 1.
Next, we solve the characteristic equation for A:
|A - λI| = |1 - λ| = 0.
Setting the determinant equal to zero, we find that the eigenvalue λ = 1.
To find the eigenvector associated with the eigenvalue 1, we solve the equation (A - λI)X = 0:
(1 - 1)X = 0,
0X = 0.
The resulting equation 0X = 0 implies that any vector X will satisfy the equation.
Learn more about coefficient matrix here:
https://brainly.com/question/9879801
#SPJ11
Calculate the area of the regular pentagon below:
A regular pentagon with side length of 22.3 inches and dotted line from center to middle of side of 15.4 inches.
(4 points)
a
686.84 square inches
b
732.34 square inches
c
858.55 square inches
d
1717.1 square inches
Answers
The area of the regular pentagon is approximately 732.34 square inches.
What is Polygon?A polygon is a plane figure that is described by a finite number of straight line segments connected to form a closed polygonal chain.
To calculate the area of a regular pentagon, we can use the formula:
Area = (1/4) ×√(5(5 + 2√5)) × side²
the side length of the pentagon is 22.3 inches, we can substitute this value into the formula:
Area = (1/4)√(5 (5 + 2√5)) (22.3)²
Area = 732.34 square inches
Therefore, the area of the regular pentagon is approximately 732.34 square inches.
To learn more on Polygons click:
https://brainly.com/question/24464711
#SPJ1
HELPPPPPP: Simplify - {- [- (-8) ] }
Answers
Answer:
\(-8\)
Step-by-step explanation:
Just take away parentheses.
How do u find the fraction result of this equation,
Im confused

Answers
At step 2, we arrive at
(2x + 3) (x + 3) = 0
and the next step (which isn't actually shown) is to use the so-called zero-product property that says if \(ab=0\), then \(a=0\) or \(b=0\). This means
2x + 3 = 0 or x + 3 = 0
and solving the first equation leads to the rational solution.
2x + 3 = 0
2x = -3
x = -3/2
A chocolate bar contains 6 grams of fat. If you eat no fewer than 5 and no more than 9 bars, how many grams of fat will you consume?
Answers
5 x 6 = 30
9 x 6 = 54
54 + 30 = 84
you would be intaking 84 grams of fat
what is 6/5 of 3792????????? PLEASE HELP ME
Answers
Answer:
4550.4 ?
Step-by-step explanation:
I'm not sure tho dddd
lines l and m are parallel
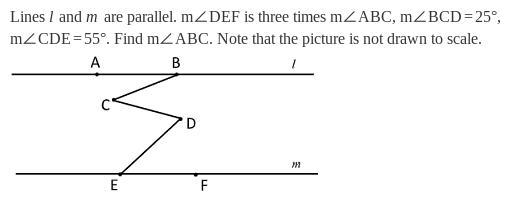
Answers
Answer:
m∠ABC = 15°Step-by-step explanation:
Given
m∠ABC = x°m∠BCD = 25°m∠CDE = 55°m∠DEF = 3x°Add two more parallel lines passing through points C and D.
Consider alternate interior angles formed by the four parallel lines.
The angles between the two middle lines are equal to:
m∠BCD - m∠ABC = m∠CDE - m∠DEFSubstitute values and solve for x:
25 - x = 55 - 3x3x - x = 55 - 252x = 30x = 15m∠ABC = 15°
Determine the fugacity and fugacity coefficients of methane using the Redlich-Kwong equation of state at 300 K and 10 bar. Write all the assumptions made.
Answers
Using the Redlich-Kwong equation of state at 300 K and 10 bar, the fugacity and fugacity coefficients of methane are 13.04 bar and 1.304, respectively.
The Redlich-Kwong equation of state for fugacity is given as:
f = p + a(T, v) / (v * (v + b))
The fugacity coefficient is given as:
φ = f / p
Where, f is the fugacity, p is the pressure, a(T, v) and b are constants given by Redlich-Kwong equation of state. Now, applying the Redlich-Kwong equation of state at 300 K and 10 bar, we have the following:
Given: T = 300 K; P = 10 bar
Assumptions:
It is assumed that the volume of the gas molecules is negligible and the intermolecular forces between the molecules are negligible. The equation of state is a cubic equation and has three roots, but only one root is physical.The constants, a(T, v) and b are expressed as follows:
a(T, v) = 0.42748 * (R ^ 2 * Tc ^ 2.5) / Pc,
b = 0.08664 * R * Tc / Pc
Where R is the gas constant, Tc and Pc are the critical temperature and pressure, respectively.
Now, substituting the given values in the above equations, we have:
Tc = 190.56 K; Pc = 45.99 bar
R = 8.314 J / mol * K
For methane, we have:
a = 0.42748 * (8.314 ^ 2 * 190.56 ^ 2.5) / 45.99 = 1.327 L ^ 2 * bar / mol ^ 2
b = 0.08664 * 8.314 * 190.56 / 45.99 = 0.04267 L / mol
Using the above values, we can now calculate the fugacity of methane:
f = p + a(T, v) / (v * (v + b))= 10 + 1.327 * (300, v) / (v * (v + 0.04267))
Since the equation of state is cubic, we need to solve for v numerically using an iterative method. Once we get the value of v, we can calculate the fugacity of methane. Now, substituting the value of v in the above equation, we get:
f = 13.04 bar
The fugacity coefficient is given as:
φ = f / p= 13.04 / 10= 1.304
Therefore, the fugacity and fugacity coefficients of methane using the Redlich-Kwong equation of state at 300 K and 10 bar are 13.04 bar and 1.304, respectively. Assumptions made in the above calculations are: The volume of the gas molecules is negligible. The intermolecular forces between the molecules are negligible. The equation of state is a cubic equation and has three roots, but only one root is physical.
Learn more about Redlich-Kwong equation:
https://brainly.com/question/29566070
#SPJ11
a store can sell 20 electric shavers per day at $25 per shaver, but he can sell 30 shavers if he charges $20 per shaver. find the demand equation, assuming that is linear.
Answers
Let the demand equation be defined as D = a - bp. So, the answer is: the demand equation is linear and is given by: D = 50 - 1.2p.
The equation be defined as D = a - bp. Where D = Demand in Units P = Pricea = Maximum units that can be sold at zero price b = Price elasticity of demandThe first thing to do is to find the values of 'a' and 'b' given the two sets of data.
That is, for P = $25, D = 20 and for P = $20, D = 30. For P = $25, D = 20, D = a - bp, 20 = a - 25, bb = (a - 20)/25. .........(1)
For P = $20, D = 30, D = a - bp, 30 = a - 20, bb = (a - 30)/20. .........(2)
Equating (1) and (2), (a - 20)/25 = (a - 30)/20
Cross multiplying and simplifying, 4a - 200 = 5a - 150a = 50
Therefore, substituting into (1), b = (50 - 20)/25 = 1.2.
Thus, the demand equation is: D = a - bp = 50 - 1.2p. Therefore, the demand equation is linear and is given by: D = 50 - 1.2p.
For more questions on: equation
https://brainly.com/question/29174899
#SPJ8
A is at 0 radians with coordinates (1, 0) on the unit circle. Point B is the result of
point A rotating - 5π/4 radians. Name two other angles of rotation that take A to B. At least one must be negative. Explain your reasoning.

Answers
The two other angles of rotation that take A to B are
3π/4 radians-13π/4 radiansHow to find the two other anglesIf we wish to rotate point A on the unit circle by a negative 5π/4 radians, one method is to begin at point A and proceed clockwise with an angle of 5π/4 radians. Negative angles denote counterclockwise movement.
When attempting to find another rotation that transports A to B, we may augment -5π/4 radians by 2π (or multiples of 2π), yielding:
-5π/4 + 2π = 3π/4 radians
Alternatively, subtracting multiples of 2π from -5π/4 radians results in yet another rotation taking A to B:
-5π/4 - 2π = -13π/4 radians
Learn more about unit circle at
https://brainly.com/question/29268357
#SPJ1
write the ratio in simplest form
30/55
Answers
Answer:
6:7
Step-by-step explanation:
Hope it helps
#CARRY ON LEARNING
The numerator and denominator can each be divided by five. Once the denominator has been divided by five, it is now prime. That is as far as you can go.
5. Terry descends 110 feet in 10 minutes inside a cave. What is Terry's change
in position before descending?
Answers
Answer:
The correct option would be D: -110 feet / 10 minutes
Calculate the number of hours needed to frame a one-story house 36' long, in which 2 x 6 x 16 joists will be placed 16" OC (round your answer to nearest whole number. ) A. 4 B. 7 C. 6 D. 5?
Answers
6 Joists are horizontal framing members used to support ceilings or floors, and they're usually made of wood. The correct option is option C. 6.
It should be remembered that the number of joists and their thicknesses must be determined by the intended loading. So, we have to calculate the number of joists needed in order to frame a one-story house 36 feet long, in which 2 x 6 x 16 joists will be placed 16 inches apart in the center. So, we have:
Number of joists required= Total length of house/spacing of joist + 1
= (36×12) / 16 + 1= 28.5 + 1= 29.5 ≈ 30
Therefore, 30 joists are required.
Also, since there are 30 joists and each joist is 16 feet long, the total length of the joists is:
Total length of joists = Length of each joist × Number of joists
= 16 × 30 = 480 feet
Therefore, 480 feet of framing material is required.
To calculate the number of hours required for framing, we can use the following formula:
Time required = (Total length of framing / Length of each piece) × Time required per piece
The time required per piece depends on the type of work, the skill level of the workers, and the equipment being used. Therefore, we can only assume that the time required per piece is 1 hour. So,
Time required = (480 / 16) × 1= 30 × 1= 30
Therefore, 30 hours are required to frame the house. Therefore, the correct option is C. 6.
You can learn more about skill level at: brainly.com/question/31301960
#SPJ11
A school needs to buy new notebook and desktop computers for its computer lab. The notebook computers cost $300 each, and the laptop computers cost $350 each. How much would it cost to buy 18 notebooks and 12 desktop computers? How much would it cost to buy nn notebooks and dd desktop computers?
Answers
Answer:
$9,600
Step-by-step explanation:
notebook computer : $300
laptop computer : $350
18 x 300 = 5,400
12 x 350 = 4,200
4,200 + 5,400 = 9,600
A company orders boxed lunches from a deli, which all cost the same price. The
relationship between the number of boxed lunches ordered, x, and the total cost in
dollars of the lunches, y, is represented by a graph drawn in the xy-plane.
If the point (5, 35) lies on the graph, what does the ordered
pair (5, 35) Indicate?

Answers
Answer:
The ordered pair (5, 35) in this context indicates that 5 boxed lunches were ordered and the total cost of those lunches was $35.
In the given graph, the x-coordinate represents the number of boxed lunches ordered (in this case, 5), and the y-coordinate represents the total cost of the lunches (in this case, $35). The point (5, 35) indicates the specific combination of the number of boxed lunches and the corresponding total cost on the graph.
If there are 16 people in a hospital and 4 need an xray.
What is the probabilty that if you choose 2 people randomly, exactly one will need an xray?
Answers
The probability that if you choose 2 people randomly, exactly one will need an x-ray is 0.4.
The probability that if you choose 2 people randomly from the 16 in the hospital, exactly one will need an x-ray is as follows:
Firstly, calculate the probability of choosing one person who needs an X-ray and one person who doesn't.
There are 4 people who need an x-ray and 12 who don't, so the probability for this is (4/16) * (12/15).
Now, calculate the probability of choosing one person who doesn't need an X-ray and one person who does. This is (12/16) * (4/15).
Now, add the probabilities to find the total probability.
The probability that exactly one person will need an x-ray is
(4/16) * (12/15) + (12/16) * (4/15) = 2/5
=0.4.
Learn more about probability:
https://brainly.com/question/251701
#SPJ11
The probability that if you choose 2 people randomly, exactly one will need an x-ray is 0.4 or 40%.
If there are 16 people in a hospital and 4 need an xray, the probability that if you choose 2 people randomly, exactly one will need an xray is 0.56.
Total number of people in a hospital = 16
Number of people who need an x-ray = 4
Thus, the probability that if you choose 2 people randomly, exactly one will need an x-ray is given by;
P(one needs an x-ray) = (Number of people who need an x-ray × Number of people who do not need an x-ray) / Total number of people × Total number of people - 1
P(one needs an x-ray) = (4 × 12) / 16 × 15
P(one needs an x-ray) = 0.08
P(one doesn't need an x-ray) = (Number of people who need an x-ray × Number of people who do not need an x-ray) / Total number of people × Total number of people - 1
P(one doesn't need an x-ray) = (12 × 4) / 16 × 15
P(one doesn't need an x-ray) = 0.32
Now, we have to add both the probabilities of exactly one person needing an x-ray and exactly one person not needing an x-ray;
P(exactly one person needs an x-ray) = P(one needs an x-ray) + P(one doesn't need an x-ray)
P(exactly one person needs an x-ray) = 0.08 + 0.32P(exactly one person needs an x-ray) = 0.4
The probability that if you choose 2 people randomly, exactly one will need an x-ray is 0.4 or 40%.
learn more about 'probability'
#SPJ11
Question 1 (Multiple Choice Worth 1 points)
(06.03 LC)
Choose the correct simplification of the expression
a
b
a1⁰b5
Answers
The correct simplification of the expression is 25x^2y^22.
How to calculate the expressionIt is important to note that an expression is simply used to show the relationship between the variables that are provided or the data given regarding an information.
x mn = x ^ m×n = xmn
xm× xn = x m+n
= (5)2(x)^2(y5)^2(y3)^4
= 25x^2y10y^12
= 25x^2y^22
Therefore, the correct simplification of the expression is 25x^2y^22.
Learn more about expressions on:
https://brainly.com/question/1859113
#SPJ1
Choose the correct simplification of the expression (5xy5)2(y3)4.
25x2y22, 10x2y22, 25x3y14, 10x3y14
Find the maximum rate of change of f at the given point and the direction in which it occurs.
f(s,t)= te^(st), (0,2)
Answers
The maximum rate of change of function f at the given point occurs in the direction of the gradient vector.
How to find maximum rate of change?To find the maximum rate of change of a function f at a given point, we need to compute the gradient of the function and evaluate it at that point. The gradient represents the direction of steepest ascent, and its magnitude indicates the maximum rate of change.
By finding the partial derivatives of f with respect to each variable and evaluating them at the given point, we obtain the components of the gradient vector. The maximum rate of change occurs in the direction of this gradient vector. Without the specific function and point, it is not possible to determine the exact maximum rate of change or its direction.
Learn more about rate of change
brainly.com/question/29181688
#SPJ11
This is me. What is 50+ 50?

Answers
Answer:
100
tvtvtvtcxtexxxtuncd,d,w
Answer:
100
Step-by-step explanation:
because 50 + 50 = 100
a factory makes rods by cutting plastic pipes that are 4 feet long into 7 equal sized rodshow long is each rod?what is the total length of 15 rods?
Answers
As a fraction, length of the 15 rods = 8 4/7 feet
As decimal, length = 8.57 feet
Explanation:initial length pipes = 4 feet
Dividing the length of the pipe into 7:
\(\begin{gathered} length\text{ }of\text{ each rod = }\frac{initial\text{ length}}{7\text{ parts}} \\ length\text{ }of\text{ each rod }=\frac{4}{7}\text{feet} \end{gathered}\)length of 15 of those rods:
\(\begin{gathered} \text{length = 15 }\times\text{ length of each rod} \\ \text{length = 15 }\times\text{ }\frac{4}{7} \end{gathered}\)\(\begin{gathered} length\text{ of 15 rods = }\frac{60}{7} \\ Total\text{ length of 15 rods = 8}\frac{4}{7}\text{ or 8.57 f}eet \end{gathered}\)Given the figure below, find the values of x and z.
(10x - 65)
(9x - 49)

Answers
(10x - 65) = (9x - 49)
By subtracting 9x in both sides,
(10x - 9x) - 65 = (9x -9x) - 49
x - 65 = -49
By adding 65 in both sides,
x - 65 + 65= -49 + 65
x = 16
Next, to find the value of z, it’s important to know that the straight line has 180 degrees. Then you would substitute the x value you found into one of your equation and subtract it from 180.
10 (16) - 65 = 160 - 65 = 95
Now you know that (10x - 65) degrees is equal to 95 degrees,
180 - 95 = z = 85
Answer: x = 16
z = 85
please show full step by step explanation, solve number 9 first

Answers
Problem N 9
we have that
UW=UV+VW -----> by addition segment postulate
substitute given values
(2x-8)=(x-8)+(12)
solve for x
2x-8=x+4
2x-x=4+8
therefore
The answer is
x=12i really need help pls

Answers
Answer:
x=7
Step-by-step explanation:
\((15x + 3) = 108 \\ 15x = 108 - 3 \\ 15x = 105 \\ x = 7\)
1. For the solid bounded by the panes 2 = 1 - x and z=1-y in the first octant (which is the same as being bounded by x = 0, y = 0, 2 = 0), one triple integral that describes the volume of the solid is: 1- SL | 1 d:dyds + C5 .** 1 dzdyudar 0 lo z , Z=1-4 ។ Z=1- х Find three other orders of integration that describe this solid. You need not find the volume. 2. Compute by switching the order of integration: dyd.x 3. Write the following integral in polar coordinates, then solve. arctan ( dyda ", 1.
Answers
1. For the solid bounded by the panes 2 = 1 - x and z=1-y in the first octant, one triple integral that describes the volume of the solid. The region is bounded by the x-axis and the curve y = √(2x-x^2), which is the top half of a circle centered at (1,0) with radius 1.
One possible order of integration is:
∫0^1 ∫0^(1-x) ∫0^(1-y) dzdydx
This means we integrate over z first, then y, then x. Another order of integration could be:
∫0^1 ∫0^x ∫0^(1-x-y) dzdydx
Here we integrate over z first, then x, then y.
Another possible order of integration is:
∫0^1 ∫0^1-x ∫0^1-y dzdxdy
Here we integrate over z first, then x, then y. This order of integration can also be rewritten in polar coordinates as:
∫0^(π/4) ∫0^(secθ-1) ∫0^(cscθ-1) r dzdrdθ
2. Compute by switching the order of integration:
∫0^2 ∫0^√(2x-x^2) dydx
First, let's sketch the region of integration. The region is bounded by the x-axis and the curve y = √(2x-x^2), which is the top half of a circle centered at (1,0) with radius 1.
We can switch the order of integration to integrate over x first, then y:
∫0^1 ∫0^(2-2y^2) dxdy
To find the limits of integration for x, we set y = √(2x-x^2) and solve for x:
y^2 = 2x - x^2
x^2 - 2x + y^2 = 0
(x-1)^2 = 1 - y^2
x = 1 ± √(1-y^2)
Since the curve is the top half of the circle, we take the positive square root:
x = 1 + √(1-y^2)
So the limits of integration for x are 0 to 2-2y^2. Integrating with respect to x first gives:
∫0^1 ∫0^(2-2y^2) dxdy = ∫0^1 (2-2y^2)dy = 4/3
3. Write the following integral in polar coordinates, then solve:
arctan (dy/dx)
We can write dy/dx in terms of polar coordinates using the chain rule:
dy/dx = (dy/dr)(dr/dθ)(1/dx/dθ)
Using the relationships x = rcosθ and y = rsinθ, we have:
dx/dθ = -rsinθ
dy/dθ = rcosθ, So
dy/dx = (dy/dr)(dr/dθ)(1/dx/dθ) = (cosθ)/(sinθ) = cotθ
Therefore, the integral becomes:
∫arctan(cotθ) dθ
To solve this integral, we use the identity arctan(x) + arctan(1/x) = π/2 for x > 0:
arctan(cotθ) = π/2 - arctan(tanθ)
So the integral becomes:
∫(π/2 - arctan(tanθ)) dθ
Integrating, we get:
(π/2)θ - ln|cosθ| + C
Where C is the constant of integration.
1. To find three other orders of integration for the solid bounded by the planes z = 1 - x, z = 1 - y, x = 0, y = 0, and z = 0 in the first octant, we can rearrange the given triple integral, which is given as:
∫∫∫_D dz dy dx
Now, we can find three other orders of integration:
a) ∫∫∫_D dx dz dy
b) ∫∫∫_D dy dx dz
c) ∫∫∫_D dy dz dx
2. To compute the volume of the solid by switching the order of integration, we can rewrite the given integral ∫∫ dy dx as: ∫∫ dx dy
Visit here to learn more about first octant:
brainly.com/question/30711212
#SPJ11
The area covered by a lake is 11 square kilometers. It is decreasing exponentially at a rate of 2 percent each year and can be modeled by A(t) = 11×(0. 98)^t.
A. By what factor does the area decrease after 10 years?
B. By what factor does the area decrease each month?
Answers
A. The area decreases by a factor of about 0.6565 after 10 years. B. The area decreases by a factor of about 0.0197 each month.
A. To find the factor by which the area decreases after 10 years, we need to compare the initial area (at t=0) to the area after 10 years (at t=10). We can use the formula for A(t) to calculate these values:
A(0) = 11 square kilometers (initial area)
A(10) = 11 ×(0.98)¹⁰ ≈ 7.22 square kilometers (area after 10 years)
The factor by which the area decreases after 10 years is the ratio of A(10) to A(0):
A(10) / A(0) ≈ 7.22 / 11 ≈ 0.6565
So the area decreases by a factor of about 0.6565 after 10 years.
B. To find the factor by which the area decreases each month, we need to first find the annual rate of decrease, and then convert it to a monthly rate. We know that the area decreases by 2 percent each year, so the annual rate of decrease is 0.02. To find the monthly rate of decrease, we can use the formula:
r = (1 + i)^(1/n) - 1
where:
r is the monthly rate of decrease
i is the annual rate of decrease (0.02 in this case)
n is the number of months in a year (12)
Plugging in the values, we get:
r = (1 + 0.02)^(1/12) - 1 ≈ 0.00165
So the area decreases by a factor of approximately:
(1 - r)¹² ≈ (1 - 0.00165)¹² ≈ 0.0197 each month. Therefore, the area decreases by a factor of about 0.0197 each month.
To learn more about area here:
https://brainly.com/question/27683633
#SPJ4
Don’t know need help

Answers
I think that the answer would be 14
at a certain high school, the prom committee is going to choose new members. there are students from the junior class and students from the senior class who are willing to be new members. in how many ways can new members be chosen if more than must be from the senior class?
Answers
Answer:
Step-by-step explanation:
7 students from the Junior class.
6 students from the Senior class.
4 new members are to be chosen.
Required: Find the number of ways 4 new members can be chosen if 2 or fewer must be from the senior class. So, Therefore, the correct answer is 560 ways.
an triangle has a angle of 75 degrees, x and y are the missing angles but x is twice y, what are the possibilities of x and y?
Answers
Answer:
x = 70°
y = 35°
Step-by-step explanation:
Given one angle of a triangle is 75° and the other two are 'x' and 'y', you want to find the possible values of 'x' and 'y' when x = 2y.
SetupThe angle sum theorem and the given relation give rise to two equations:
75 +x +y = 180
x = 2y
SolutionUsing the second equation to substitute for x in the first equation, we have ...
75 +(2y) +y = 180
3y = 105 . . . . . . . . . subtract 75 and simplify
y = 105/3 = 35
x = 2y = 2(35) = 70
The measures of angles x and y are 70° and 35°, respectively.
Finding probability, please help!! show all work!!

Answers
Answer:
9/28 and 32.1%
Step-by-step explanation:
So the sample space consists of all products for (5 * 1, 5 * 2, 5 * 3.... and the same thing for 6, 7, and 8)
This gives you the sample space: {5, 10, 15, 20, 25, 30, 6, 12, 18, 24, 30, 36, 7, 14, 21, 28, 35, 42, 8, 16, 24, 32, 40, 48}.
The size of the sample space is 4 * 6, since for each number (5, 6, 7, 8), there are 6 products (the dice have six numbers). This means the sample space has 24 combinations, you can also verify this by manually counting the sample space.
Now filtering the sample space so you only get a product that is 28 or higher you get: {30, 30, 36, 28, 35, 42, 32, 40, 48} which has 9 possible combinations that have a product greater than or equal to 28. Divide this by the entire sample space and you get a probability of: 9/28, which in decimal form is approximately: \(0.3214\). Multiplying this by 100 gives you: \(32.1\)%