Martin is filling his bathtub, but he left the drain partially open. Martin
knows that it takes 8 minutes to fill his 40-gallon tub. The equation
v = 2. 5t represents the volume, v, of water that drains out of the tub in
t minutes. If Martin leaves the water on, will the tub ever overflow? Use
unit rates to justify your answer.
Answers
Yes, the tub will overflow if martin leaves the water on with the given velocity and time equation.
As, in the 8 minutes 40 gallon tub can be filled by martin.
According to the equation, v=2.5t,
Now, if we convert the equation in terms of time,
then the equation becomes for 40 minutes=8 gallons,
the equation is 5 minutes=1 gallon
Now, if we transform this equation in terms of v and t the equation becomes, 5t=1v
5t=v
and another equation that we have is, 2.5t=v
Now, the equation 5t=v represent the water entering in the tub while 2.5t=v represent the water flowing out from the tub.
And by the equations we can understand that water entering in the tub will always be twice the water flowing out from the tub. So, if martin leaves the tap on then the water will overflow.
Learn more about equation
brainly.com/question/23856265
#SPJ4
Related Questions
Use the ratio test to find the radius of convergence of the power series.
1+2x+4!x^2/(2!)^2+6!x^3/(3!)^2+8!x^4/(4!)^2+10!x^5/(5!)^2
Answers
The radius of convergence is 1. Let's apply the ratio test to determine the radius of convergence of the given power series:
r = lim |(a_{n+1}/a_n)|
n->inf
where a_n is the nth term of the series.
In this case, we have:
a_n = (2n-1)!x^(n-1)/(n-1)!(2!)^(n-1)
So, applying the ratio test, we get:
r = lim |(a_{n+1}/a_n)|
n->inf
= lim |[(2n+1)!x^n/n!(2!)^n)/(2n-1)!x^(n-1)/(n-1)!(2!)^(n-1)]|
= lim |[(2n+1)x/(n+1)(2!)]|
= lim |(2n+1)/(n+1)|*|x/2|
= 2|x/2|
We know that the series converges if r < 1 and diverges if r > 1. Therefore, the series converges when:
2|x/2| < 1
|x| < 1
So the radius of convergence is 1.
Learn more about convergence here:
https://brainly.com/question/14394994
#SPJ11
A walking path across a park is represented by the equation y=-3x - 3.A
new path will be built perpendicular to this path. The paths will intersect at
the point (-3,6). Identify the equation that represents the new path.
Answers
Answer:
\(y=\frac{1}{3} x+7\)
Step-by-step explanation:
We need to find the equation of a line perpendicular to \(y=-3x-3\), which passes through the point (-3, 6).
Recall that a line perpendicular to a line of the form: \(y=mx+b\), must have a slope which is the opposite of the reciprocal of the slope of the original line. that is, a slope of the form;
\(slope=-\frac{1}{m}\)
Then, in our case, since the original line has slope "-3", a perpendicular line to it should have a slope given by:
\(slope=-\frac{1}{-3} =\frac{1}{3}\)
We now know the slope, and also a point for this new line, so we use the point-slope form of a line:
\(y-y_0=m_\perp\,(x-x_0)\\y-6=\frac{1}{3} (x-(-3))\\y-6=\frac{1}{3} x+\frac{3}{3} \\y-6=\frac{1}{3} x+1\\y=\frac{1}{3} x+7\)
Let A(0, 0, 0), B (4, -1,1), C(0, 1,2), and D(3, 1, 2)) be points in R^3. Find the
(a) vectors of length 10 orthogonal to both AC and AD.
(b) volume of the parallelepiped with adjacent edges consisting of the vectors AB, AC, and AD.
(c) cosines of the angles that AC makes with the three coordinate axes.
Answers
The cosines of the angles that AC makes with the x-, y-, and z-axes are 0, 1/√5, and 2/√5, respectively.
How to find the vectors orthogonal to given planes?(a) To find a vector of length 10 orthogonal to both AC and AD, we first need to find the normal vector to the plane containing AC and AD. This can be done by taking the cross product of AC and AD:
N = AC × AD = (0-1)(2-1)i - (0-2)(3-2)j + (1-1)(3-1)k = -i - j + k
Now, we need to find a vector in the direction of N that has length 10. We can do this by scaling N by a factor of 10/|N|:
v = (10/√3)i + (10/√3)j - (10/√3)k
Therefore, the vector of length 10 orthogonal to both AC and AD is v.
How to find the volume of a parallelepiped?(b) The volume of the parallelepiped with adjacent edges consisting of the vectors AB, AC, and AD is given by the scalar triple product:
V = |AB · (AC × AD)|
We can first find AC × AD:
AC × AD = (0-1)(2-2)i - (0-2)(3-0)j + (1-1)(3-3)k = -2j
Then, we can find AB:
AB = (4-0)i + (-1-0)j + (1-0)k = 4i - j + k
Taking the dot product of AB and -2j, we get:
AB · (AC × AD) = (4i - j + k) · (-2j) = -2j
Taking the absolute value of -2j, we get:
V = |-2j| = 2
Therefore, the volume of the parallelepiped with adjacent edges consisting of the vectors AB, AC, and AD is 2.
How to find direction cosines of a given vector in R^3?(c) To find the cosines of the angles that AC makes with the three coordinate axes, we can use the direction cosines. The direction cosines of a vector v are given by:
cos α = v_x / |v|
cos β = v_y / |v|
cos γ = v_z / |v|
where α, β, and γ are the angles that v makes with the x-, y-, and z-axes, respectively.
For AC = <0, 1, 2>, we have:
|AC| = √(0^2 + 1^2 + 2^2) = √5
cos α = 0 / √5 = 0
cos β = 1 / √5
cos γ = 2 / √5
Therefore, the cosines of the angles that AC makes with the x-, y-, and z-axes are 0, 1/√5, and 2/√5, respectively.
Learn more about vectors orthogonal, parallelepiped, direction cosines.
brainly.com/question/31400571
#SPJ11
if your aircraft was cleared for the ils rwy 18 at lincoln municipal and crossed the lincoln vortac at 5,000 feet msl, at what point in the teardrop could a descent to 3,200 feet commence? a. only at the point authorized by atc. b. immediately. c. as soon as intercepting loc in bound.
Answers
At 8000 feet MSL in the teardrop could a descent to 3,200 feet commence.
What is aircraft?
A vehicle that can fly is known as an aircraft. It does so by getting help from the air. It does this by either employing static lift, the dynamic lift of an airfoil or, in a few rare instances, the downward push from jet engines. Aerial vehicles include, but are not limited to, planes, helicopters, airships (including blimps), gliders, paramotors, and hot air balloons.
As given, your aircraft was cleared for the ils rwy 18 at Lincoln municipal and crossed the Lincoln Vortac at 5,000 feet MSL.
Therefore, at 8000 feet MSL in the teardrop could a descent to 3,200 feet commence.
To know more about the aircraft, click on the link
https://brainly.com/question/5055463
#SPJ4
solve 4 with exponent -4 without the exponent in other words
4 exponent -4 without exponent
Answers
Answer:
\( \frac{4}{1} \times \frac{4}{1} \times \frac{4}{1} \times \frac{4}{1} = \frac{256}{1} = - 256\)
Step-by-step explanation:
I dont know if I'm right or not
but this is how I learned it
20 applicants from a pool of 90 applications will be hired. How many ways are there to select the applicants who will be hired?
Answers
The ways are the \(C_{20} ^{90}\) which are we there to select the applicants who will be hired with the help of combination.
According to the statement
we have to find that the number of ways are there to select the applicants who will be hired.
So, For this purpose, we know that the
A combination is a mathematical technique that determines the number of possible arrangements in a collection of items where the order of the selection does not matter.
Here we use the combination.
And from the given information:
20 applicants from a pool of 90 applications will be hired.
And according to this the combination becomes:
\(C_{20} ^{90}\)
then solve it
\(C_{20} ^{90} = \frac{90!}{20! (70!)}\)
\(C_{20} ^{90} = \frac{90*89*88*87*86*85*84*83*82!}{20*19*18*17*16*15*14!}\)
Then after solve it
\(C_{20} ^{90} = \frac{89*11*87*43*14*83*82!}{19*14!}\)
Now open another factorial
\(C_{20} ^{90} = \frac{89*11*87*43*14*83*82*81*80*79*78*77*76*75*74*73*72*71}{19*14*13*12*11*10*9*8*7*6*5*4*3*2*1}\)
Now solve this then
\(C_{20} ^{90} = {89*11*87*43*83*82*79*15*74*73*71}\).
So, The ways are the \(C_{20} ^{90}\) which are we there to select the applicants who will be hired with the help of combination.
Learn more about combination here
https://brainly.com/question/11732255
#SPJ4
Example 14.11:
A deck of playing cards has 52 cards, divided into four suits (diamonds, spades, clubs, and hearts). There are an equal number of cards in each suit in this deck. If three cards are drawn, what is the probability that the first two cards drawn are clubs and the last is red? There are three events in this problem:
• Let event A = first card drawn is a club, • Let event B = second card drawn is a club • C = third card drawn is red. We want to find P(A and B and C) (i.e. the probability that the first card drawn is a club AND the second card drawn is a club AND the third card drawn is a red card).
Refer to Example 14.11 Suppose the three events are independent. Use the Multiplication Rule to find P(A and B and C). Round answer to FOUR decimal places. 0.0312
Answers
To find the probability of event A (first card drawn is a club), event B (second card drawn is a club), and event C (third card drawn is red), we can use the Multiplication Rule for independent events.
Given that the events are independent, the probability of all three events occurring is the product of their individual probabilities.
Let's calculate the probability step by step:
1. Probability of event A: P(A) = Number of clubs / Total number of cards
There are 13 clubs in a deck of 52 cards, so P(A) = 13/52 = 1/4.
2. Probability of event B: P(B) = Number of clubs (after one club is drawn) / Total number of remaining cards
After one club is drawn, there are 12 clubs left out of 51 remaining cards, so P(B) = 12/51 = 4/17.
3. Probability of event C: P(C) = Number of red cards / Total number of remaining cards
There are 26 red cards (diamonds and hearts) out of 50 remaining cards, so P(C) = 26/50 = 13/25
Now, using the Multiplication Rule:
P(A and B and C) = P(A) * P(B) * P(C) = (1/4) * (4/17) * (13/25) = 0.03117647059.
Rounding this result to four decimal places, we get approximately 0.0312.
Therefore, the probability that the first two cards drawn are clubs and the last card is red is approximately 0.0312.
To learn more about probability, refer below:
https://brainly.com/question/11034287
#SPJ11
Answers to questions A and B

Answers
Answer:
A. m(arc BC) = 16°
B. m(arc BAC) = 344°
Step-by-step explanation:
From the picture attached,
AB is the diameter of the circle.
Since, measure of an arc is always same as the central angle of arc.
Therefore, m(arc AC) = m(∠ADC) = 164°
m(arc AB) = 180°
m(arc BC) = 360° - m(arc AB) + m(arc AC)
= 360° - (180° + 164°)
= 360° - 344°
= 16°
m(arc BAC) = m(arc AB) + m(arc AC)
= 180° + 164°
= 344°
Please answer the following question to show that you understand the theorems
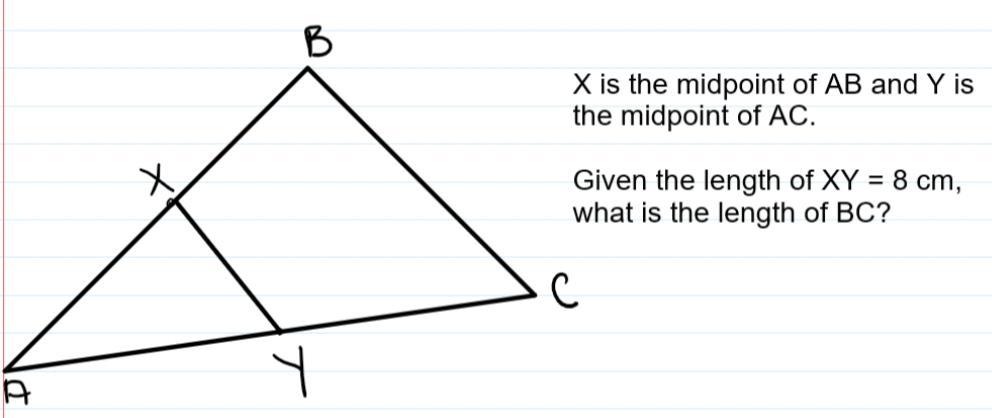

Answers
Using the mid-point theorem of triangle, the length of BC is 16cm.
What is the mid-point theorem of triangle?The Mid-Point Theorem is one of the key concepts in geometry that addresses the characteristics of triangles.
According to the midpoint theorem, "The line segment in a triangle joining the midpoint of any two of the triangle's sides is said to be parallel to its third side and is also half the length of the third side."
Given that, X is the mid point of AB and Y id the mid point of AC.
length of XY = 8 cm
By the mid-point theorem of triangle, the line segment of joining the midpoint of two sides of a triangle is always half and parallel to third line.
So that, XY = 1/2 of BC
SO, BC = 2* XY
BC = 2*8 cm
BC = 16cm
So, the length of BC is 16cm.
To learn more about mid-point theorem visit:
brainly.com/question/19505549
#SPJ1
an amusement park charges $4.25 for admission, plus $1.50 for each ride ticket. Chase has $30 to spent on admission and ride tickets
Answers
Answer:
he went on 16 rides and paid for 2 admission
Step-by-step explanation:
he went on 16 rides and paid for 2 admission
As a measure of intelligence, mice are timed when going through a maze to reach a reward of food. The time (in seconds) required for any mouse is a random variable Y with a density function given by f(y) = b y2 , y ≥ b, 0, elsewhere, where b is the minimum possible time needed to traverse the maze. (a) Show that f(y) has the properties of a density function
Answers
Using the properties of densit function,
we get that f(y) has satisfied property of a density function. So, it a density function.
A probability density function, or density function, returns the value of a function at a given value of x.
The probability density function must satisfy two requirements:
f(x) must be non-negative for all values of the random variable.Integral of all values of random variable must equal 1.We have given that, Y is a random variable and
b f(y) = by² , y>b
where , b --> the minimum possible time needed to traverse the maze.
we have check that f(y) is Probability density function or not . For this check above two requirements ,
(i) f(y) ≥ 0 for all y > 0
so, it's satisfied
(ii) Integral over all values of the random variable ₓ∫ⁿ f(y)dy = ₓ∫ⁿ(b/y²)dy where n=∞ and x = b
= ₓ[ -b/y]ⁿ
= -(0-1) = 1
Hence , f(y) is density function.
To learn more about Density function, refer:
https://brainly.com/question/20815791
#SPJ4
A person places $6770 in an investment account earning an annual rate of
7.6%, compounded continuously. Using the formula V = Pert, where Vis
the value of the account in t years, P is the principal initially invested, e is the
base of a natural logarithm, and r is the rate of interest, determine the
amount of money, to the nearest cent, in the account after 13 years.
Answers
The future value in 13 years when compounded continuously is; $18183.25
How to solve Continuous Compounding?Continuous compounding is defined as the process of calculating interest and reinvesting it into an account's balance over an infinite number of periods.
The formula for continuous compounding is;
V = Pe^(rt)
where;
V is the value of the account in t years
P is the principal initially invested
e is the base of a natural logarithm.
r is the rate of interest
We are given;
P = $6770
r = 7.6% = 0.076
t = 13
Thus;
V = 6770 * e^(0.076 * 13)
V = $18183.25
Read more about Continuous Compounding at; https://brainly.com/question/30460031
#SPJ1
if f(x) =4x²+1 and g(x) =x²-5, find (f-g)(x)
Answers
Answer:
(f-g)(x)=4x^2+1-x^2+5
=3x^2+6
=3(x^2+2)
Choose the benchmark that 3-7/12
closest to
3-1/2
2.
3
Answers
Answer:
3
Step-by-step explanation:
What is the unit rate of the graph seen below? Please explain it in Real World Terms.

Answers
The unit rate of the graph is 2 inches per hour of snowfall where X axis represents time in hours and Y axis represents snowfall in inches.
What is unit rate?
A unit rate is the rate of change in a relationship where the rate is per 1.
In a graph, change in y coordinate with respect to x is unit rate.
According to the given question:
X axis of the graph represents time in hours.
Y axis represents snowfall in inches
Therefore the given graph gives information about the height of snowfall per hour during Misty Mountain Storm.
From the given graph clearly 2 units of y changes 1 unit with respect to x
The coordinates can be related as (1, 2), (2, 4), (3, 6), (4, 8) and (5, 10) check the attachment below
Hence 2 inches of snow falls in 1 hour, 4 inches of snow falls in 2 hour, 6 inches of snow falls in 3 hour, 8 inches of snow falls in 4 hour and 10 inches of snow falls in 5 hour.
So, the unit rate of graph is 2 inches per hour of snowfall.
To know more about unit rate visit
https://brainly.com/question/22047550
#SPJ9

What is the equation of the line that passes through the point (-6,6) and has a slope of 1/3
Answers
Answer:y=1/3x+8
Step-by-step explanation:
Plug it into point slope form
y-6=1/3(x+6)
y-6=1/3x+2
+6. +6
y=1/3x+8
The number of miles M that a certain automobile can travel onone gallon of gasoline at a speed of v mi/hr is given by:
M=-(1/30)v^2 + (5/2)v , for v<0<70
a. Find the most economical speed for a trip.
b. Find the largest value of M.
Answers
a. The most economical speed for a trip is v = 35 mph. and b. The largest value of M is M = 87.5 miles.
a. To find the most economical speed for a trip, we need to maximize the value of M, which represents the number of miles the automobile can travel on one gallon of gasoline.
Given equation: M = -(1/30)v² + (5/2)v
Take the derivative of M with respect to v using the power rule for derivatives:
dM/dv = -(2/30)v + (5/2)
Set the derivative equal to 0 and solve for v to find the critical point:
-(2/30)v + (5/2) = 0
-(2/30)v = -(5/2)
v = (5/2) * (30/-2)
v = 35
Since v must be less than 70 according to the given range, the most economical speed for the trip is v = 35 mph.
b. To find the largest value of M, we can substitute the given expression for M into the equation and evaluate it for the given range of v, which is v < 0 < 70.
Given equation: M = -(1/30)v² + (5/2)v
Substitute v = 70 into the equation to find the largest value of M:
M = -(1/30)(70)² + (5/2)(70)
M = -4900/30 + 350/2
M = -163.33 + 175
M = 11.67
Therefore, the largest value of M is M = 87.5 miles. (rounded to two decimal places)
To know more about speed, refer here:
https://brainly.com/question/17661499#
#SPJ11
what is the sum of 7x/x²-4 and 2/xt2?
Answers
Answer: i might be wronge but 9x - 4 / x^2
Step-by-step explanation:
A quantity with an initial value of 7200 decays exponentially at a rate of 0.3% every
day. What is the value of the quantity after 10 weeks, to the nearest hundredth?
Answers
Answer:5834.36 You're welcome
Answer:5834.36
Step-by-step explanation:
what is the value of the median for the following set of scores? scores: 1, 3, 4, 6, 8, 12, 13, 23, 25, 26 group of answer choices 10 12.5 7 8
Answers
The median is the middle number of the set. The middle number in this set is 12.5. Therefore, the median is 12.5.
To find the median of a set of numbers, you need to first arrange the numbers in numerical order. The numbers from the given set, arranged in numerical order, are:
1, 3, 4, 6, 8, 12, 13, 23, 25, 26
The median is the middle number of the set. The middle number in this set is 12.5. Therefore, the median is 12.5.
Learn more about median here
https://brainly.com/question/15323584
#SPJ4
What is 4/9 closest to 0,1/2 or 1
Answers
Answer:
1/2
Step-by-step explanation:
4/9 is equal to 4.444 repeating so that would be closest to 1/2
About what percentage of the data lies within 2 standard deviations of the mean in a normal distribution? 47. 5% 68% 95% 99. 7%.
Answers
The percentage of data that lies within 2 standard deviations of the mean in a normal distribution is 95%.
A normal distribution is a probability distribution that is symmetric around the mean of the distribution. This means that the there are more data around the mean than data far from the mean. A normal distribution is also known as the Gaussian distribution. When depicted on a graph, a normal distribution is bell-shaped.
For a normal distribution:
About 68% of the data lie within one standard deviation of the mean. About 95% of the data lie within two standard deviations of the mean. About 99.7% of the data lie within three standard deviations of the mean.Please find attached an image of a normal distribution. A similar question was answered here: https://brainly.com/question/17101164

Answer:
I believe it is 95%
Step-by-step explanation:
Can you help me with this answer

Answers
Answer:
169 (second choice)
Step-by-step explanation:
\(13 [6^2 / (5^2-4^2) + 9]\)
\(13 [6^2 / (25 - 16) + 9]\)
\(13 [6^2 / 9 + 9]\)
13 [36 / 9 + 9]
13 [4 + 9]
13 [13]
169
Help please!!! thank you so much I almost have English but I never completed this math homework on time that was due yesterday. So thank you and please help!

Answers
2) Answer is 7.5
5) Answer is 32
7) 51
8) 22
(It’s easy just use BIDMAS, meaning B= brackets, i= indices, D= Division, M= Multiplication, A= Addition, S= Subtraction)
Can you guys help me with this

Answers
Answer:
11) 40
12)113
13) 105
11) 180-65-75
12) 180 - (180-62-51)
13) 360-100-60-95
65+75=140
180-140=40
F=40
2) finding x:
62+51=113
180-113= 67
X=67
We can know how much y equals from the two angles far away which we already calculated so y=113
C) all angles should add up to 360
100+95+60= 255
360-255=105
X=105
Hope this helps
Convert the following equation into Standard Form.

Answers
Answer:
answer
Step-by-step explanation:
5y=6y+5 thanks
Answer:
Look It Up
Step-by-step explanation:
what is the slope of the line that contains the points

Answers
Answer: 0
Step-by-step explanation:
The slope of a line that contains the points (13, -2) and (3, -2) would be 0, since the y-coordinate of both points is the same. The slope of a line is determined by the difference in the y-coordinates of the two points, divided by the difference in their x-coordinates. In this case, the difference in the y-coordinates is 0, so the slope is 0.
A particle moving in the x−y plane has a position vector given by r=1.35t
2
i+1.22t
3
j, where r is in inches and t is in seconds. Calculate the radius of curvature rho of the path for the position of the particle when t=2.2 sec. Sketch the velocity v and the curvature of the path for this particular instant. Answer: rho= in.
Answers
The radius of curvature of a particle's path in the x-y plane at t=2.2 sec is 94.25 inches, found using velocity and acceleration vectors. Sketch shows velocity and curvature vectors.
To find the radius of curvature rho, we need to first find the velocity vector v and the acceleration vector a at t=2.2 sec.
The position vector of the particle is given by:
r = 1.35t^2 i + 1.22t^3 j
Differentiating this with respect to time t gives the velocity vector:
v = dr/dt = 2.7t i + 3.66t^2 j
Differentiating again with respect to time t gives the acceleration vector:
a = dv/dt = 2.7 i + 7.32t j
Now, to find the radius of curvature rho, we use the formula:
rho = |v|^3 / |a|*sin(theta)
where |v| is the magnitude of the velocity vector, |a| is the magnitude of the acceleration vector, and theta is the angle between v and a.
At t=2.2 sec,
|v| = |2.7(2.2) i + 3.66(2.2)^2 j| = 11.209 in/sec
|a| = |2.7 i + 7.32(2.2) j| = 16.416 in/sec^2
theta = angle between v and a
To find theta, we can use the dot product:
v . a = |v| |a| cos(theta)
cos(theta) = (v . a) / (|v| |a|)
cos(theta) = (2.7)(2.7) + (3.66)(2.2)^2 / (11.209)(16.416)
cos(theta) = 0.503
theta = cos^-1(0.503) = 1.042 radians
Substituting these values into the formula for rho, we get:
rho = (11.209)^3 / (16.416)(sin(1.042))
rho = 94.25 in
Therefore, the radius of curvature of the path for the position of the particle when t=2.2 sec is 94.25 inches.
To sketch the velocity vector v and the curvature of the path at this instant, we can draw the vectors at the position of the particle for t=2.2 sec. The velocity vector v has a magnitude of 11.209 in/sec and is directed at an angle of approximately 67 degrees above the x-axis. The curvature vector points towards the center of curvature of the path and has a magnitude of 1/rho.
know more about curvature vectors here: brainly.com/question/31032113
#SPJ11
Gavin bakes 70 cookies in an hour.How many cookies can he bake in 4hours
Answers
He can bake 280 cookies
Answer: 280 cookies
Step-by-step explanation:
.In order to increase the value of the F statistic, which of the following must occur?
a. MSwithin > MSbetween
b. MSwithin = MSbetween
c. MSwithin < MSbetween
d. Ratio = 1
Answers
If MSwithin is smaller than MSbetween, then increasing MSwithin and/or decreasing MSbetween will lead to an increase in the F statistic.
How the F statistic is calculated?The F statistic is calculated by dividing the variance between groups (MSbetween) by the variance within groups (MSwithin). Therefore, to increase the value of the F statistic, either the numerator (MSbetween) needs to increase, or the denominator (MSwithin) needs to decrease.
So, the answer is:
a. MSwithin > MSbetween
If the variance within groups (MSwithin) is reduced or the variance between groups (MSbetween) is increased, the F statistic will increase. Therefore, if MSwithin is smaller than MSbetween, then increasing MSwithin and/or decreasing MSbetween will lead to an increase in the F statistic.
Learn more about statistic
brainly.com/question/31538429
#SPJ11