Need help please thanks

The value of the measure of a smallest angle is, ∠ x = 25°

Given that angles are given with measure

(x+17)

(7x-16)

115°

Hence, By definition of the triangle;

The measure of angles is,

(x+17) + (7x-16)+ 115°= 180

8x + 116 = 180

8x = 64

x = 8

The value of the measure of a smallest angle is,

(x+17) = 8 + 17 = 25 degree

To learn more about the angle visit:;

brainly.com/question/25716982

#SPJ1

Answer:

Refer to the step-by-step explanation, please follow along very carefully. Answers are encased in two boxes.

Step-by-step explanation:

Given the following function, find it's derivative using the definition of derivatives. Evaluate the function when θ=1, 11, and 3/11

\(p(\theta)=\sqrt{11\theta}\)

\(\hrulefill\)

The definition of derivatives states that the derivative of a function at a specific point measures the rate of change of the function at that point. It is defined as the limit of the difference quotient as the change in the input variable approaches zero.

\(f'(x) = \lim_{{h \to 0}} \dfrac{{f(x+h) - f(x)}}{{h}}\)\(\hrulefill\)

To apply the definition of derivatives to this problem, follow these step-by-step instructions:

Step 1: Identify the function: Determine the function for which you want to find the derivative. In out case the function is denoted as p(θ).

\(p(\theta)=\sqrt{11\theta}\)

Step 2: Write the difference quotient: Using the definition of derivatives, write down the difference quotient. The general form of the difference quotient is (f(x+h) - f(x))/h, where "x" is the point at which you want to find the derivative, and "h" represents a small change in the input variable. In our case:

\(p'(\theta) = \lim_{{h \to 0}} \dfrac{{p(\theta+h) - p(\theta)}}{{h}}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h}\)

Step 3: Take the limit:

We need to rationalize the numerator. Rewriting using radical rules.

\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11(\theta + h)} - \sqrt{11\theta} }{h} \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11\theta + 11h} - \sqrt{11\theta} }{h}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h}\)

Now multiply by the conjugate.

\(p'(\theta)= \lim_{h \to 0} \dfrac{\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} }{h} \cdot \dfrac{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} } \\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{(\sqrt{11}\sqrt{\theta+h} - \sqrt{11}\sqrt{\theta} )(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )} \\\\\\\)

\(\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11h}{h(\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} )}\\\\\\\Longrightarrow p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\)

Step 4: Simplify the expression: Evaluate the limit by substituting the value of h=0 into the difference quotient. Simplify the expression as much as possible.

\(p'(\theta)= \lim_{h \to 0} \dfrac{11}{\sqrt{11}\sqrt{\theta+h} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta+(0)} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{\sqrt{11}\sqrt{\theta} + \sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11}\sqrt{\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\\\\\\\Longrightarrow p'(\theta)= \dfrac{11}{2\sqrt{11\theta} }\)

\(\therefore \boxed{\boxed{p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta} }}}\)

Thus, we have found the derivative on the function using the definition.

It's important to note that in practice, finding derivatives using the definition can be a tedious process, especially for more complex functions. However, the definition lays the foundation for understanding the concept of derivatives and its applications. In practice, there are various rules and techniques, such as the power rule, product rule, and chain rule, that can be applied to find derivatives more efficiently.\(\hrulefill\)

Now evaluating the function at the given points.  

\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}; \ p'(1)=??, \ p'(11)=??, \ p'(\frac{3}{11} )=??\)

When θ=1:

\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(1)= \dfrac{\sqrt{11} }{2\sqrt{1}}\\\\\\\therefore \boxed{\boxed{p'(1)= \dfrac{\sqrt{11} }{2}}}\)

When θ=11:

\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(11)= \dfrac{\sqrt{11} }{2\sqrt{11}}\\\\\\\therefore \boxed{\boxed{p'(11)= \dfrac{1}{2}}}\)

When θ=3/11:

\(p'(\theta)= \dfrac{\sqrt{11} }{2\sqrt{\theta}}\\\\\\\Longrightarrow p'(\frac{3}{11} )= \dfrac{\sqrt{11} }{2\sqrt{\frac{3}{11} }}\\\\\\\therefore \boxed{\boxed{p'(\frac{3}{11} )= \dfrac{11\sqrt{3} }{6}}}\)

Thus, all parts are solved.

Answer:

200 ml

Step-by-step explanation:

She uses a ml of solution a.

She uses b ml of solution b.

Equation of the amount of each solution:

a = b - 100

Equation of the amount of alcohol:

0.11a + 0.2b = 51

0.11(b - 100) + 0.2b = 51

0.11b - 11 + 0.2b = 51

0.31b = 62

b = 200

Answer: 200 ml

Answer:

Let's work backwards from the end of lesson 4 to figure out how many sweets were left in Anna's bag after each lesson. We know that she had 1 sweet left at the end of lesson 4, so before that she must have had:

Lesson 4: 1 sweet + 1 sweet for teacher + 1 sweet left over = 3 sweets

Lesson 3: (3 sweets + 1 sweet for teacher) x 2 = 8 sweets

Lesson 2: (8 sweets + 1 sweet for teacher) x 2 = 18 sweets

Lesson 1: (18 sweets + 1 sweet for teacher) x 2 = 40 sweets

So, Anna started with 40 sweets in her bag.

Answer:

Axis of Symmetry: x = -4

Vertex: ( -4, -6 )

Step-by-step explanation:

~ Part I ~

1. To find the axis of symmetry, rewrite y = x^2 + 8x + 10 in the parabola standard form ( 4p( y - k ) =  ( x - h) ^2 for an up-down facing parabola at  vertex ( h, k ) and a focal length |p|) ⇒ 4 * 1/4 ( y - ( - 6 ) ) = ( x - ( - 4 ) )^2

2. Therefore the parabola properties are ⇒ ( h, k ) =  ( - 4, -6 ), p = 1/4

3. Answer: x = -4

~ Part II ~

1. From the previous question, we got that the vertex should be ⇒ ( -4, -6 )

2. Answer: ( -4, -6 )

The Intel pays $7,760 to Bally Manufacturing on August 14.

The first step in calculating what Intel Corporation pays Bally on August 14 is to determine the net price of the machinery after the trade discount and the return of $100 due to defects.

The trade discount of 40% is calculated as follows:

Discount = List price × Discount rate

Discount = $13,100 × 0.40 = $5,240

So the net price of the machinery after the trade discount is:

Net price = List price - Discount

Net price = $13,100 - $5,240 = $7,860

After Intel returns $100 of machinery, the cost of the machinery is further reduced to:

Net price after return = Net price - Return

Net price after return = $7,860 - $100 = $7,760

Since the payment terms are 3/10 EOM (end of month), Intel receives a discount of 3% if payment is made within 10 days. The 10-day period begins on August 1 and ends on August 10 (the payment due date). Since Intel pays the bill on August 14, payment is late and the 3% discount does not apply.

For such more questions on pays

https://brainly.com/question/25793394

#SPJ8

x

−

1

x−1?x

)

=

2

x

4

−

3

x

+

3

f(x)=2x

4

−3x+3, then what is the remainder when

f

(

x

)

f(x) is divided by

x

−

1

x−1?

Based on the given conditions, the lock solution is 205.

To solve the lock, to calculate the total score based on the given conditions:

Crocus: + 20

Daffodil: + 25

Snowflake: - 50

Tulip: + 30

Bird-Red: + 25, else + 10

Calculating the scores for each input:

TULIP: +30

CROCUS: +20

DAFFODIL: +25

TULIP: +30

DAFFODIL: +25

TULIP: +30

DAFFODIL: +25

CROCUS: +20

Total score = 30 + 20 + 25 + 30 + 25 + 30 + 25 + 20 = 205

Therefore, the solution for the lock is 205.

Find out more on lock solution here: https://brainly.com/question/19191108

#SPJ1

Image transcribed:

SPRING NOW LOADING.

<IF CROCUS, THEN +20>

<IF DAFFODIL, THEN +25>

<IF SNOWFLAKE, THEN -50>

<IF TULIP, THEN +30>

<IF BIRD-RED, THEN +25, ELSE + 10>

TULIP

CROCUS

DAFFODIL

TULIP

DAFFODIL

TULIP

DAFFODIL

CROCUS

Solve Lock

Answer:

165 minutes

Step-by-step explanation:

To solve for the number of minutes that Joaquin played for, we can use this expression:

(let 'a' represent how much time passed from the time Joaquin started playing basketball until the time he arrived at home)

Subtracting 1:10 from each side:

1:10 - 1:10 cancels out to 0, while 3:35 - 1:10 is equal to 2:25.

So, the expression is now:

So, 2 hours and 25 minutes passed.

If we know that 1 hour is equivalent to 60 minutes, we can use this expression to solve for however many minutes are in 2 hours:

Now we need to add on the number of minutes and the time it took him to get home:

Therefore, 165 minutes passed from the time Joaquin started playing basketball until the time he arrived at home.

1.1. Accumulated depreciation:

The accumulated depreciation for the machine bought on 1 July 2013 would be R150,000 as of 31 March 2016.

1.2. Machine realization:

The machine bought in 2013 was sold for R120,000 on 30 June 2015, resulting in a profit/loss on the sale of R10,000.

1.1. Accumulated Depreciation:

To calculate the accumulated depreciation, we need to determine the annual depreciation expense for each machine and then accumulate it over the years.

Machine bought on 1 July 2013:

Cost: R250,000

Depreciation rate: 20% per annum on cost

Depreciation expense for the year ended 31 March 2014: 20% of R250,000 = R50,000

Depreciation expense for the year ended 31 March 2015: 20% of R250,000 = R50,000

Depreciation expense for the year ended 31 March 2016: 20% of R250,000 = R50,000

Accumulated depreciation for the machine bought on 1 July 2013:

As of 31 March 2014: R50,000

As of 31 March 2015: R100,000

As of 31 March 2016: R150,000

1.2. Machine Realisation:

To record the sale of the machine bought in 2013, we need to adjust the machine's value and the accumulated depreciation.

Machine's original cost: R250,000

Accumulated depreciation as of 30 June 2015: R100,000

Net book value as of 30 June 2015:  

R250,000 - R100,000 = R150,000.

On 30 June 2015, the machine was sold for R120,000.

Realisation amount: R120,000

To record the sale:

Debit Cash: R120,000

Debit Accumulated Depreciation: R100,000

Credit Machine: R250,000

Credit Machine Realisation: R120,000

Credit Profit/Loss on Sale of Machine: R10,000 (difference between net book value and realisation amount).

These entries will reflect the appropriate balances in the ledger accounts and properly close off the accounts for the years ended 31 March 2016.

For similar question on depreciation.

https://brainly.com/question/15998639  

#SPJ8

Since each of the data value is multiplied by 5, the new mean will be 5 times the original mean.

To get the original mean, we need to divide by 5.

Therefore the original mean is given by:

Answer: 8

Answer:

2,4,6,

6,12,18

10,20,30

The statement " when adding an entry to a binary search tree, the search ends at a leaf if the entry is not already in the tree" is true.

A tree is a type of data structure made up of nodes and contains the following features:

1- Every tree has a root node (also known as a parent node) at the top that contains some value (can be any datatype).

2- There are 0 or more child nodes of the root node.

3- There are zero or more child nodes for each child node, and so forth. As a result, the tree gains a subtree. Each node has a separate subtree that consists of its offspring and their offspring, etc. This implies that any node can function as a tree on its own.

In addition, a binary search tree (BST) has the following two features:

1- Each node has a maximum of up to two children.

2-For each node, the values of its left descendent nodes are less than that of the current node, which in turn is less than the right descendent nodes (if any).

To know more about binary search trees visit: brainly.com/question/29734003

#SPJ4

The statement about the unit prices which is true is Kitty Kibbles has a lower unit price of $1.30/pound.

The correct answer choice is option D.

Cost of 16-pound bag of Kitty Kibbles = $20.80

Unit price of kitty kibbles = Price / number of pounds

= $20.80 / 16

= $1.30 per pound.

Cost of 8-pound bag of Feline flavor = $11.20

Unit price of feline flavor = Price / number of pounds

= $11.20 / 8

= $1.40 per pound

Ultimately, the unit price of kitty kibbles and feline flavor is $1.30 and $1.40 respectively.

Complete question:

A 16-pound bag of Kitty Kibbles is $20.80. An 8-pound bag of Feline Flavor is $11.20. Which statement about the unit prices is true?

A. Feline Flavor has a lower unit price of $1.40/pound.

B. Feline Flavor has a lower unit price of $1.30/pound.

C. Kitty Kibbles has a lower unit price of $1.40/pound.

D. Kitty Kibbles has a lower unit price of $1.30/pound.

Read more on unit price:

https://brainly.com/question/945712

#SPJ1

Answer:

600

Step-by-step explanation:

Answer: 0.086 0r 8.6%

Step-by-step explanation:

Divide 1280.54 / 14,890 = 0.086

The sales tax rate for this purchase was approximately 8.6%.

Gertrude got a used car for $14,890; she has paid $1,280.54 as a sales tax.

We need to determine sales tax rate for this purchase,

To determine the sales tax rate for Gertrude's car purchase, we need to calculate the ratio of the sales tax amount to the initial price of the car and express it as a percentage.

Sales tax rate = (Sales tax amount / Car price) x 100

Given that Gertrude paid $1,280.54 as sales tax and the car's price was $14,890, we can substitute these values into the formula:

Sales tax rate = (1,280.54 / 14,890) x 100

Calculating this expression gives us:

Sales tax rate = (0.0859) x 100

Sales tax rate ≈ 8.6

Therefore, the sales tax rate for this purchase was approximately 8.6%.

Learn more about sales tax rate click;

https://brainly.com/question/29751934

#SPJ2

The numerical value of x in the similar pair of triangle is 10.

A ratio is simply the relation between two amounts showing how many times a value is contained within another value.

From the diagram,

Side A of the small triangle = 10

Side B of the small triangle = x + 2

Side A of the Big triangle = 10 + x

Side B of the big triangle = x + 14

Hence;

Ratio of Side A to Side B of the small triangle = 10 / x + 2

Ratio of Side A to Side B of the Big triangle = 10 + x / x + 14

Since the triangle area similar, equate the two ratio and solve for x.

10 / ( x + 2 ) = ( 10 + x ) / ( x + 14 )

Cross multiply

10( x + 14 ) = ( 10 + x )( x + 2 )

Expand using FOIL method

10x + 140 = 10x + 20 + x² + 2x

10x + 140 = x² + 12x + 20

x² + 12x + 20 = 10x + 140

x² + 12x + 20 - 10x - 140 = 0

x² + 2x - 120 = 0

Factor the left side of the equation

( x - 10 )( x + 12 ) = 0

Hence;

x - 10 = 0 and x + 12 = 0

x = 10 and x = -12

Since the dimension of the triangle cannot be negative,

x = 10

Therefore, the value of x is 10.

Learn more about FOIL Method here: brainly.com/question/28527940

#SPJ1

1. In the calculation, only one pound of fish food is shared equally among one aquarium.

2. Each of the aquarium gets one pound of fish food

To solve the first part of the problem, we need to find the value of P when 1/2 ÷ 8 = P. By doing the calculation by hand, we get:

1/2 ÷ 8 = 0.0625. So, the  P = 0.0625.

In the second part of the problem, we know that 1 pound of fish is shared equally among a certain number of aquariums, and we need to find that number.

Since each aquarium gets 1 pound of fish food, and the total amount of fish food is 1 pound, we can set up an equation to solve for the number of aquariums:

1 pound of fish food / X number of aquariums = 1 pound of fish food per aquarium

Simplifying the equation, we get:

X = 1 pound of fish food / 1 pound of fish food per aquarium

X = 1 aquarium

Therefore, the pound of fish food is shared equally among 1 aquarium, and each aquarium gets 1 pound of fish food.

Read more about aquarium

brainly.com/question/28889858

#SPJ1

Answer:

942.50

Step-by-step explanation:

725×30% or 0.3 = 217.5

217.5+725=942.5

Solution:

Given:

From the probability, it can be deduced that as the number of trials increases, the observed frequency will get closer to the expected frequency.

Therefore, if the number of trials increases significantly, then the observed frequency of landing heads up gets closer to the expected frequency based on the probability of the coin landing heads up.

Answer:

0.5 miles

Step-by-step explanation:

...

Domain: 8, 9, 10, 11.Range: -7, 7 This relation does not represent a function because the same x-value (8, 10, 11) is associated with more than one y-value (-7, 7).

Domain: 8, 9, 10, 11

Range: -7, 7

A function is a relation between a set of inputs and a set of outputs such that each input is associated with exactly one output. This particular relation fails to meet this condition because the domain value 8 is associated with two different range values (-7 and 7). In other words, the same input (8) is associated with two different outputs, which means the relation does not represent a function. The domain of the relation is 8, 9, 10, 11 and the range is -7 and 7. Therefore, this relation does not represent a function because it violates the condition that each input must have one and only one associated output.

Learn more about function here

https://brainly.com/question/29633660

#SPJ4

Part A: The total area of the brick paver border is \(960\) square feet.

Part B: The total cost of the brick pavers needed for this project is $\(7,680\).

Part A: To find the total area of the brick paver border, we need to subtract the area of the pool from the area of the larger rectangle. The area of the pool is \(32\) feet multiplied by 12 feet, which is equal to \(384\)square feet.

The area of the larger rectangle is \(48\) feet multiplied by \(28\) feet, which is equal to \(1,344\) square feet. Therefore, the area of the brick paver border is \(1,344\) square feet minus \(384\) square feet, which equals \(960\) square feet.

Part B: If brick pavers cost $\(8\)per square foot, we can calculate the total cost by multiplying the cost per square foot by the total area of the brick paver border. The total area of the brick paver border is \(960\) square feet, and the cost per square foot is $\(8\).

Therefore, the total cost of the brick pavers needed for this project is $\(8\)multiplied by \(960\) square feet, which equals $\(7,680\).

Note: The calculations provided assume that the border consists of a single layer of brick pavers.

For more such questions on area:

https://brainly.com/question/2607596

#SPJ8

Answer and Step-by-step explanation:

I think this is correct? The directions aren't very clear/descriptive, so sorry if this is wrong.

A.

1. wins:games

2. wins:losses

3. losses:wins

4. games played:wins

5. losses:games played

B.

1. 8:12, or 2:3

2. 3:7

3. 5:3

4. 12:15, or 4:5

5. 20:25, or 4:5

#teamtrees #PAW (Plant And Water)

Answer:

1/(1) (2) +1/(2) (3)

=1/2+1/6

=3

Answer:

12 feet

Step-by-step explanation:

this is a rectangle! because DC = 16 feet, you know that AB is also equal to 16 feet

therefore, DA + CB = 24

because ABCD is a rectangle, you know that DA = CB and you can use substitution to say that CB + CB = 24

2CB = 24

CB = 12

Focus on Gamble B only. Multiply each winnings with their corresponding probabilities.

5100*0.50 = 2550

200*0.25 = 50

0*0.25 = 0

Add up those results: 2550+50+0 = 2600

The expected value of gamble B is $2600

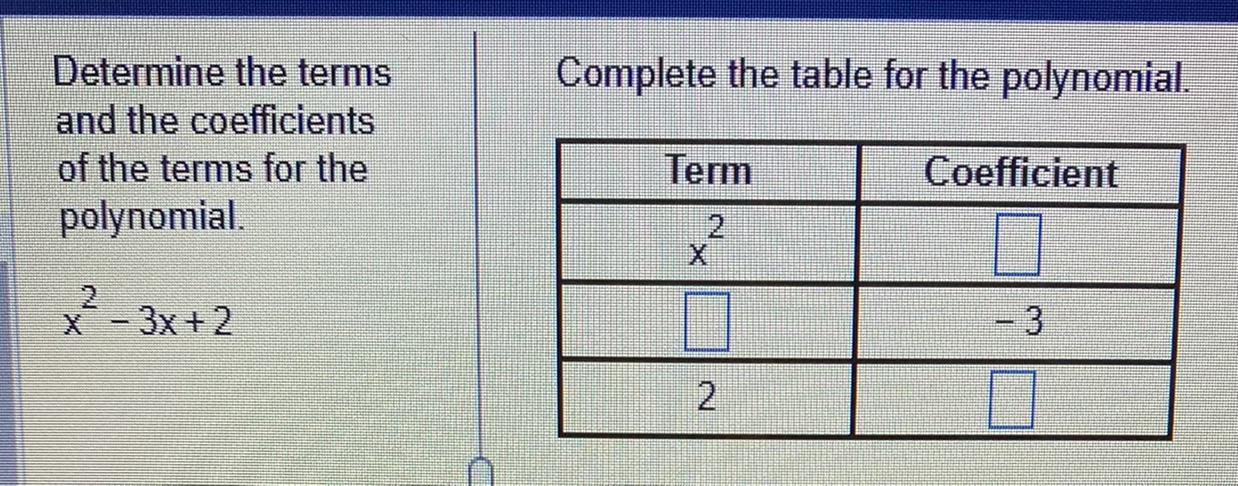
Answers in bold

\(\begin{array}{|c|c|} \cline{1-2}\text{Term} & \text{Coefficient}\\\cline{1-2}\text{x}^2 & \boldsymbol{1}\\\cline{1-2}\boldsymbol{-3\textbf{x}} & -3\\\cline{1-2}2 & \boldsymbol{2}\\\cline{1-2}\end{array}\)

Explanation:

The given expression \(\text{x}^2-3\text{x}+2\) is the same as \(\text{x}^2+(-3\text{x})+2\)

This leads to the three terms as shown in the table above. Each term is separated by a plus sign.

The coefficient is the number to the left of the variable. Think of \(\text{x}^2\) as \(1\text{x}^2\) and think of \(2\) as \(2\text{x}^0\)

In other words, \(\text{x}^2-3\text{x}+2\) is the same as \(1\text{x}^2+(-3\text{x})+2\text{x}^0\)

The explanatory variable is the clients while the response variable is change in duration.

A causal relationship is said to exist between variables whereby the occurrence of an event is as a result of another event.

In a causal relationship between variables, a value may represent explanatory variable while another value may represent a response variable.

An explanatory variable is the variable where observation of changes are being made such as the clients while the response variable are the outcome of the observation such as the duration of the run by each client.

Learn more about variables here:

https://brainly.com/question/25223322

#SPJ1