Planes the fly at high speeds and low elevations have radar systems that can determine the range of an obstacle and the angle of elevation to the top of the obstacle. The radar of a plane flying at an altitude of 20,000 feet detects a tower that is 25,000 feet away, with an angle of elevation of 1 $\degree$ . A picture shows a tower on a hill and a plane flying towards the tower, and a right angle is marked between plane and tower. Distance between plane and top of tower is 25 thousand feet and is the hypotenuse of the triangle, angle of elevation from plane to top of tower is labeled 1 degrees, and perpendicular height of the triangle from a point on the tower to top of the tower is h feet.
How many feet must the plane rise to pass over the tower?
Answers
Let AB be the tower with C at the top. Let P be the position of the plane such that the angle of elevation is 1°. Let the distance PC be h ft. The distance from the plane to the foot of the tower is 25,000 ft - the height of the plane above the ground (20,000 ft), which is 5,000 ft.
The distance PC is the same as the perpendicular height of the triangle. Therefore, `tan 1° = h / 25,000`. We can solve this equation for \(h: `h = 25,000 tan 1° ≈ 436.24 ft`.\) To find how many feet the plane must rise to pass over the tower, we need to find the length of the line segment CD,
which is the height the plane must rise to clear the tower. We can use trigonometry again: `tan 89° = CD / h`. Since `tan 89°` is very large, we can approximate `CD ≈ h / tan 89°`.Therefore, `\(CD ≈ 436.24 / 0.99985 ≈ 436.29 ft`\).Thus, the plane must rise approximately 436.29 feet to pass over the tower.
To know more about position visit:
https://brainly.com/question/12650352
#SPJ11
Related Questions
how to solve 2x(x+3)=2x^2+15
Answers
Answer: x = 5/2 = 2.5
Step-by-step explanation:
Given expression
2x (x + 3) = 2x² + 15
Expand parentheses and apply the distributive property
2x · x + 2x · 3 = 2x² + 15
2x² + 6x = 2x² + 15
Subtract 2x² on both sides
2x² + 6x - 2x² = 2x² + 15 - 2x²
6x = 15
Divide 6 on both sides
6x / 6 = 15 / 6
x = 15/6
\(\boxed{x=\frac{5}{2} }\)
Hope this helps!! :)
Please let me know if you have any questions
Step-by-step explanation:
2x^2 + 6x = 2x^2 + 15
2x^2-2x^2+6x=15
6x = 15
x= 5/2 when simplified
ASAP PLS
Write an equation to represent the following scenario: Ms. Cloutier’s wedding photographer requires a $1000 deposit, and then $250 for every hour she is working.
Answers
x being the number of hours she’s working
In a survey of 2,100 people who owned a certain type of car, 945 said they would buy that type of car again. What percent of the people surveyed were satisfied with the car ?
Answers
Answer:
45%
Step-by-step explanation:
86x + 109y ÷ 57y + 113× =
Answers
Answer:
86x + 109y ÷ 57y + 113x = 199x + 109/57
A sollid piece of iron in the form of a cuboid of dimensions 49cm × 33 cm× 24 cm , is moulded to form a solid sphere. find the radius of the sphere
Answers
Answer:
Radius of sphere is 21 cmStep-by-step explanation:
Given:
A sollid piece of iron in the form of a cuboid of dimensions 49cm × 33 cm× 24 cm , is moulded to form a solid sphere.To Find:
Radius of the sphereSolution:
Volume of sphere = Volume of cubiod
↠ 4/3 πr³ = LBH
↠ 4/3 × 22/7 × r³ = 49 × 33 × 24
↠ 4/3 × 22/7 × r³ = 38808
↠ 4 × 22/7 × r³ = 38808/3
↠ r³ = 38808 × 3 × 7/4 × 22
↠ r³ = 441 × 21
↠ r³ = 9261
↠ r = 21 cm
Hence,
Radius of sphere is 21 cmAnswer:
21.00 cm to the nearest hundredth.
Step-by-step explanation:
The volume of the sphere will be equal to the volume of the cuboid.
So 4/3 π r^3 = 49*33*24 where r = radius of the sphere.
r^3 = (49*33*24 ) / 4/3 π
r^3 = 38808 / 4.18879
= 9264.728
r = ∛9264.728
= 21.0028 cm.
Which of the following numbers is rational?
A. 7.885
B. Pi with cubed 2
C. 0.144
D. 91
Answers
A slice of pizza has 1,200 calories. If 520 calories are from fat, what percentage of calories are fat?
Answers
Answer:
43.33%
Step-by-step explanation:
x : 100 = 520 : 1200
x = (520 * 100)/1200
x = 520/12
x = 43.333333%
HELP ME IN QUESTION 10 PLS

Answers
Answer:
in \(5^{9}\), 9 is not an even number, nor a multiple of 2, meaning 1,953,125 isn't a square number
Step-by-step explanation:
Answer:
Photosynthesis is a process used by plants and other organisms to convert light energy into chemical energy that, through cellular respiration, can later be released to fuel the organism's metabolic activities. Wikipedi
can someone please answer this math problem for me, please answer all of them if you can

Answers
Answer:
Q5
∠3 = ∠4
Q6.
∠S + ∠T = 90°
Q7.
∠X + ∠Y = 180°
Q8.
∠1 = ∠4
Q9.
∠K = ∠L
Answer:
Q5
∠3 = ∠4
Q6.
∠S + ∠T = 90°
Q7.
∠X + ∠Y = 180°
Q8.
∠1 = ∠4
Q9.
∠K = ∠L
Step-by-step explanation:
Where is the removable discontinuity of f(x) located? x = –5 x = 0 x = –2 x = 5
Answers
On solving the provided question we can say that - the removable discontinuity of f(x) located is -5
What is discontinuity ?Discontinuous functions in graphs are those that have no connections to one another. Discontinuities come in three different flavors: removable, jump, and infinite.. If the left limit and the right limit of a function, f(x), are both different, then the function has a first-kind discontinuity at x = a. a characteristic that cannot be mathematically continuous. Continuous functions allow you to sketch without having to lift your pen. In such a case, the function is said to as discontinuous.
here,
f(x) = \(\frac{x+5}{x^2+3x-10}\)
\(x^2+3x-10\)
x(x+5) - 2(x+5)
(x+5 )(x-2 )
x = 2, -5
To know more about discontinuity visit:
brainly.com/question/28783981
#SPJ4
A company had returns of 5%, 10%, -15%, 20%, -12%, 22%, 8% in
the last few years. Compute the arithmetic average return,
geometric average return, variance, and standard deviation of
returns.
Refer to
Answers
Arithmetic average return of the company is 2.57%.Geometric average return of the company is 13%.Variance of the company is 56.Standard deviation of the company is 7.48%.
Given, Returns of the company for the last few years are 5%, 10%, -15%, 20%, -12%, 22%, 8%
Arithmetic Average return:
Arithmetic Average return = (sum of all returns) / (total number of returns)
Arithmetic Average return = (5 + 10 - 15 + 20 - 12 + 22 + 8) / 7= 18 / 7= 2.57
Therefore, the arithmetic average return of the company is 2.57%.
Geometric average return:
Geometric average return = [(1+R1) * (1+R2) * (1+R3) * …….. * (1+Rn)]1/n - 1
Geometric average return = [(1.05) * (1.1) * (0.85) * (1.2) * (0.88) * (1.22) * (1.08)]1/7 - 1= 0.13
Therefore, the geometric average return of the company is 13%.
Variance:
Variance = (sum of (return - mean return)2) / (total number of returns)
Mean return = (5 + 10 - 15 + 20 - 12 + 22 + 8) / 7= 18 / 7= 2.57
Variance = [(5-2.57)2 + (10-2.57)2 + (-15-2.57)2 + (20-2.57)2 + (-12-2.57)2 + (22-2.57)2 + (8-2.57)2] / 7= 392.12 / 7= 56
Therefore, the variance of the company is 56.
Standard Deviation:
Standard Deviation = Square root of Variance
Standard Deviation = √56= 7.48
Therefore, the standard deviation of the company is 7.48%.
Thus, Arithmetic average return of the company is 2.57%.Geometric average return of the company is 13%.Variance of the company is 56.Standard deviation of the company is 7.48%.
To know more about arithmetic average return, click here
https://brainly.com/question/28562900
#SPJ11
Let Z be a standard normal random variable. Calculate the following probabilities using the ALEKS calculator. Round your responses to at least three decimal places.
(a) P(Z > -1.23) = 0
(b) P(Z < -1.41) = 0
(c) P(0.34 <<< 2.09) = 0
Answers
The probabilities P(Z > -1.23), P(Z < -1.41), and P(0.34 << 2.09) are all equal to 0.
(a) To calculate P(Z > -1.23), we can use the standard normal distribution table or a calculator. Since the standard normal distribution is symmetric, the probability of Z being greater than -1.23 is the same as the probability of Z being less than 1.23, which is approximately 0.
(b) Similarly, to calculate P(Z < -1.41), we can use the standard normal distribution table or a calculator. The probability of Z being less than -1.41 is approximately 0.
(c) The expression P(0.34 << 2.09) indicates a range of values between 0.34 and 2.09. However, since the standard normal distribution is continuous, the probability of a single value occurring is always 0. Therefore, the probability of a range of values, like in this case, is also 0.
For more questions like Probability click the link below:
https://brainly.com/question/30034780
#SPJ11
Triple a number is 18.
Answers
hi
so 3X = 18
X = 18/3 = 6
6
Step-by-step explanation:
6 + 6 + 6 = 18
The density of a marble is 2.7g/cm3. What is the mass of th marble slab
Answers
Answer:
if the marble slab is 1 cm³ in volume the mass is 2.7 g but u did not put a volume
Solve the differential equation (Show your work). \[ 7 x^{6} \cos y d x-d y=0 \]
Answers
The solution to the given differential equation is: x⁷ cos y = y + C
where C is the constant of integration
To solve the given differential equation:
\(\[7x^6\cos y dx - dy = 0\]\)
We can separate the variables and integrate both sides.
Separating variables, we can write the equation as:
\(\[7x^6\cos y dx = dy\]\)
Now, we can integrate both sides with respect to their respective variables:
\(\[\int 7x^6\cos y dx = \int dy\]\)
Integrating the left side:
\(\[\int 7x^6\cos y dx = 7 \int x^6 \cos y dx\]\)
To integrate \(\(x^6 \cos y\)\)with respect to x, we can use integration by parts.
Let's take u = x⁶ and \(\(dv = \cos y dx\)\).
Differentiating u with respect to \(\(x\) gives \(du = 6x^5 dx\).\)
Integrating dv with respect to x gives \(\(v = \int \cos y dx = \cos y \cdot x\).\)
Applying the integration by parts formula:
\(\[\int x^6 \cos y dx = u \cdot v - \int v \cdot du\]\)
Substituting the values:
\(\[\int x^6 \cos y dx = x^6 \cdot \cos y \cdot x - \int (\cos y \cdot x) \cdot (6x^5 dx)\]\)
Simplifying:
\(\[\int x^6 \cos y dx = x^7 \cos y - 6 \int x^6 \cos y dx\]\)
Moving the integral term to the left side:
\(\[7 \int x^6 \cos y dx = x^7 \cos y\]\)
Dividing both sides by 7:
\(\[\int x^6 \cos y dx = \frac{x^7 \cos y}{7}\]\)
Now, substituting this result back into our original equation:
\(\[7 \int x^6 \cos y dx = dy\]\)
\(\[\frac{7x^7 \cos y}{7} = dy\)
Simplifying:
x⁷ cos y = dy
Finally, the solution to the given differential equation is:
x⁷ cos y = y + C
where C is the constant of integration.
To learn more about differential equations visit:
brainly.com/question/25731911
#SPJ11
A group of students weighs 500 US pennies. They find that the pennies have normally distributed weights with a mean of 3. 1g and a standard deviation of 0. 14g
Answers
a) 81.86 percent of the pennies will weigh between 2.7 and 3.3g. b) 100 percent of the pennies will weigh between 2.5 and 3.7g. c) 2.28 percent of the pennies will weigh less than 2.7g. d) 15.87 percent of the pennies will weigh more than 3.3g.
To solve these questions, we will use the properties of the normal distribution and z-scores.
a) To find the percentage of pennies that weigh between 2.7 and 3.3g, we need to calculate the area under the normal curve between these two values.
First, we need to standardize the values using z-scores:
z1 = (2.7 - 3.1) / 0.2 = -2
z2 = (3.3 - 3.1) / 0.2 = 1
Next, we can use a standard normal distribution table or a calculator to find the area between these two z-scores. The area between -2 and 1 is approximately 0.8186 or 81.86%.
Therefore, approximately 81.86% of the pennies will weigh between 2.7 and 3.3g.
b) Similarly, to find the percentage of pennies that weigh between 2.5 and 3.7g, we need to standardize the values and calculate the area between the corresponding z-scores.
z1 = (2.5 - 3.1) / 0.2 = -3
z2 = (3.7 - 3.1) / 0.2 = 3
The area between -3 and 3 encompasses the entire distribution and is equal to 1 or 100%.
Therefore, 100% of the pennies will weigh between 2.5 and 3.7g.
c) To find the percentage of pennies that weigh less than 2.7g, we need to calculate the area to the left of the corresponding z-score.
z = (2.7 - 3.1) / 0.2 = -2
Using a standard normal distribution table or a calculator, we find that the area to the left of -2 is approximately 0.0228 or 2.28%.
Therefore, approximately 2.28% of the pennies will weigh less than 2.7g.
d) To find the percentage of pennies that weigh more than 3.3g, we need to calculate the area to the right of the corresponding z-score.
z = (3.3 - 3.1) / 0.2 = 1
Using a standard normal distribution table or a calculator, we find that the area to the right of 1 is approximately 0.1587 or 15.87%.
Therefore, approximately 15.87% of the pennies will weigh more than 3.3g.
Correct Question :
A group of students weighs 500 US pennies. They find that the pennies have normally distributed weights with a mean of 3.1g and a standard deviation of 0.2g
a) What percentage of pennies will weigh between 2.7 and 3.3g?
b) What percentage of pennies will weigh between 2.5 and 3.7g
c.) What percentage of pennies will weigh less than 2.7g?
d.) What percentage of pennies will weigh more than 3.3g?
To learn more about percent here:
https://brainly.com/question/31323953
#SPJ4
In \triangle D E F, ∠ D is a right angle and tan E=3/4 . What are sin E and sec F ?
Answers
In triangle DEF where angle D is a right angle and tan E = 3/4, sin E is equal to 3/5, and sec F is equal to 5/4.
To find sin E and sec F in triangle DEF, we can use the given information that angle D is a right angle and tan E = 3/4.
First, let's find sin E. Since tan E = opposite/adjacent, we can assign the opposite side to be 3 and the adjacent side to be 4. To find the hypotenuse, we can use the Pythagorean theorem:
hypotenuse^2 = opposite^2 + adjacent^2
hypotenuse^2 = 3^2 + 4^2
hypotenuse^2 = 9 + 16
hypotenuse^2 = 25
hypotenuse = 5
Now, we have the values of the opposite and hypotenuse, so we can find sin E:
sin E = opposite/hypotenuse = 3/5
Therefore, sin E is equal to 3/5.
Next, let's find sec F. Since sec F is the reciprocal of cos F, we need to find cos F first. In a right triangle, cos F = adjacent/hypotenuse. In this case, we can assign the adjacent side to be 4 and the hypotenuse to be 5. Therefore, cos F = 4/5.
Now, we can find sec F, which is the reciprocal of cos F:
sec F = 1/cos F = 1/(4/5) = 5/4
Therefore, sec F is equal to 5/4.
In summary, in triangle DEF where angle D is a right angle and tan E = 3/4, sin E is equal to 3/5, and sec F is equal to 5/4.
Learn more about right angle here
https://brainly.com/question/24475840
#SPJ11
What are levels of central tendency (mode, median, mean) and in which type of levels of measurement would each be used?
Answers
The levels of central tendency are measures that describe the typical or central value of a dataset. The three main levels of central tendency are mode, median, and mean.
The mode is the value that occurs most frequently in a dataset and is used with nominal data, which is data that is divided into categories that cannot be ranked or ordered.
The median is the middle value in a dataset and is used with ordinal data, which is data that can be ranked or ordered but the differences between values cannot be measured.
The mean is the average value of a dataset and is used with interval and ratio data, which are both types of data that can be ranked, ordered, and have measurable differences between values. The difference between interval and ratio data is that ratio data has a true zero point, such as weight or height, while interval data does not have a true zero point, such as temperature on the Celsius or Fahrenheit scale.
In summary, the mode is used with nominal data, the median is used with ordinal data, and the mean is used with interval and ratio data.
Know more about central tendency here:
https://brainly.com/question/30218735
#SPJ11
surface area of composite figures
Answers
Answer:
mark me brainliest hope your day goes wellStep-by-step explanation:
The area of the composite figures is the area of one or more simple polygons and circles combined. We can add the areas of all the basic figures together to calculate the area of the composite figures. Find the area of each shape and add them together to find the area of the composite figure.
Answer:
The surface area is the sum of all the faces (or surfaces) of a 3D shape. Composite figures are 2 figures put together. (There is an example of a composite figure below) You find an area of both shapes and then add them together, to find the area of the full figure.
Step-by-step explanation:

Which graph represents the solution to this inequality?
-1/4(12x + 8) < -2.1 + 11
Answers
Step-by-step explanation:
-3x -2 less than 8.9
-3x less than 8.9+2
-3x less than 10.9
x =10.9/-3
Find two quadratic functions, one that opens upward and one that opens downward, whose graphs have the given x-intercepts. (-5,0), (5,0) opens upward f(x)=x²+x-5 X opens downward f(x)=x²-x+5
Answers
We have found two quadratic functions with x-intercepts (-5,0) and (5,0): f(x) =\(x^2 - 25\), which opens upward, and g(x) = \(-x^2 + 25\), which opens downward.
For the quadratic function that opens upward, we can use the x-intercepts (-5,0) and (5,0) to set up the equation:
f(x) = a(x + 5)(x - 5)
where a is a constant that determines the shape of the parabola. If this function opens upward, then a must be positive. Expanding the equation, we get:
f(x) = a(x^2 - 25)
To determine the value of a, we can use the fact that the coefficient of the x^2 term in a quadratic equation determines the shape of the parabola. Since we want the parabola to open upward, we need the coefficient of x^2 to be positive, so we can set a = 1:
f(x) = x^2 - 25
For the quadratic function that opens downward, we can use the x-intercepts (-5,0) and (5,0) to set up the equation:
g(x) = a(x + 5)(x - 5)
where a is a constant that determines the shape of the parabola. If this function opens downward, then a must be negative. Expanding the equation, we get:
g(x) = a(x^2 - 25)
To determine the value of a, we can use the fact that the coefficient of the x^2 term in a quadratic equation determines the shape of the parabola. Since we want the parabola to open downward, we need the coefficient of x^2 to be negative, so we can set a = -1:
g(x) = -x^2 + 25
For such more questions on quadratic
https://brainly.com/question/1214333
#SPJ8
Find the equations of the tangents to the curve x = 6t^2 + 4, y = 4t^3 + 4 that pass through the point (10, 8). y=?? (smaller slope)
y=?? (larger slope)
Answers
The equations of the tangents are:y = -3/2 + sqrt(37)/2(x - 10) (smaller slope)y = -3/2 - sqrt(37)/2(x - 10) (larger slope):y=-\frac{3}{2}+\frac{\sqrt{37}}{2}(x-10) (smaller slope)y=-\frac{3}{2}-\frac{\sqrt{37}}{2}(x-10) (larger slope).
Curve isx = 6t^2 + 4, y = 4t^3 + 4the slope of tangent of this curve dy/dx is dy/dx=12t/(3t^2+2)Then, equation of tangent with slope m and passing through (x1, y1) is given by(y - y1) = m(x - x1) ............(1)Here, point is (10,8)Therefore, equation of tangent passing through (10, 8) will be of the form(y - 8) = m(x - 10)Let this tangent intersect the curve at point P. Then, the coordinates of point P are given byx = 6t^2 + 4y = 4t^3 + 4.
Equating this with equation (1), we get:4t^3 + 4 - 8 = m(6t^2 - 6)4t^3 = 6m(t^2 - 1)2t^3 = 3m(t^2 - 1)2t^3 + 3mt - 3m = 0t = -m/2 ± sqrt(m^2/4 + 3m)Therefore, the two tangents are given by:y - 8 = m1(x - 10), where m1 = -3/2 + sqrt(37)/2y - 8 = m2(x - 10), where m2 = -3/2 - sqrt(37)/2Hence, the equations of the tangents are:y = -3/2 + sqrt(37)/2(x - 10) (smaller slope)y = -3/2 - sqrt(37)/2(x - 10) (larger slope):y=-\frac{3}{2}+\frac{\sqrt{37}}{2}(x-10) (smaller slope)y=-\frac{3}{2}-\frac{\sqrt{37}}{2}(x-10) (larger slope).
Learn more about slope tangent here:
https://brainly.com/question/32393818
#SPJ11
PLEASE HURRY ILL GIVE BRANILIST!!!!

Answers
The balloon that was farther from the town at the beginning, and which traveled more quickly is option D. Tasha's balloon was farther from the town at the beginning, but Henry's balloon traveled more quickly.
What is the balloon about?In order for us to know or to figure out which balloon had a faster journey, we can employ the speed equation:
Speed: Distance divided by time
Note that from the question, Henry's balloon was one that covered a distance of 16 miles within a span of 2 hours resulting in its velocity being 8 miles per hour and Tasha's balloon was situated y = 5x + 25 miles away from the town.
Theis mean that its distance from the town would be y = 5(2) + 25 = 35 miles, after a duration of 2 hours. So, Tasha's balloon covered a distance of 10 miles within a span of 2 hours, showing a speed of 5 mph.
Learn more about balloon from
https://brainly.com/question/21360487
#SPJ1
See text below
Two hot air balloons are traveling along the same path away from a town, beginning from different locations at the same time. Henry's balloon begins 15 miles from the town and is 31 miles from the town after 2 hours. The distance of Tasha's balloon from the town is represented by the function y = 5x+25.
Which balloon was farther from the town at the beginning, and which traveled more quickly?
A. Tasha's balloon was farther from the town at the beginning, and it traveled more quickly.
B. Henry's balloon was farther from the town at the beginning, and it traveled more quickly.
C. Henry's balloon was farther from the town at the beginning, but Tasha's balloon traveled more quickly.
D. Tasha's balloon was farther from the town at the beginning, but Henry's balloon traveled more quickly.
Someone please help I need to return this tomorrow
:(
Directions: Victor is making some math calculations in his head, but he makes a few mistakes. Look for the patterns in his thinking. Circle the mistakes he made and write the correct numbers in the boxes
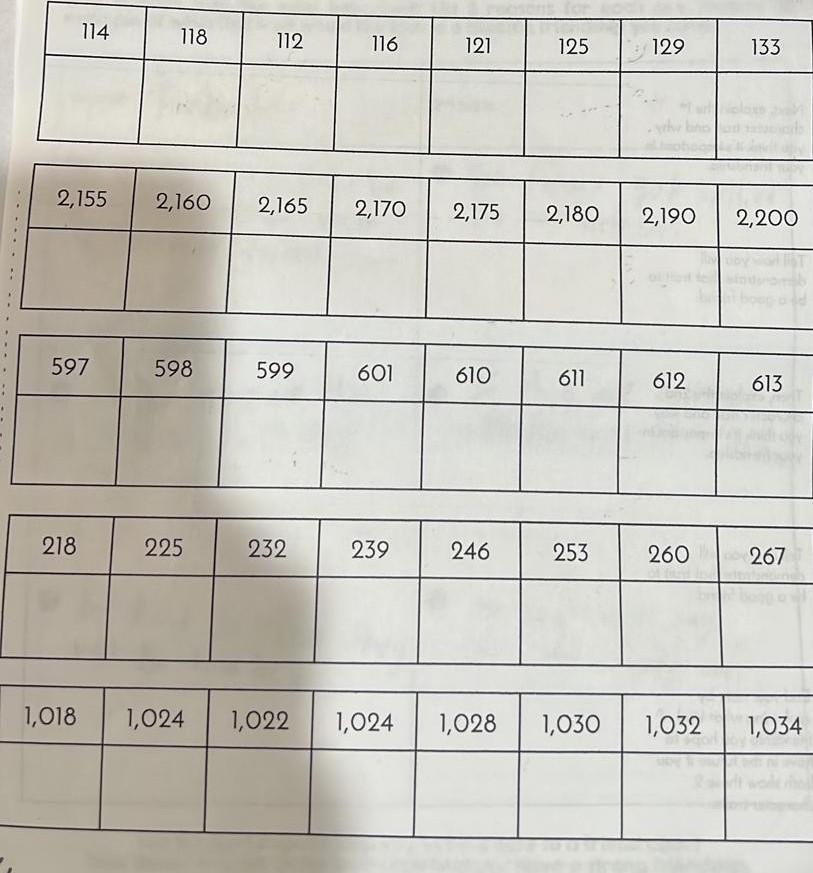
Answers
The mistakes he made in the sequence and the correct answers are (1) 121, 125, 129,133, (2) 2190 (3) 601 (4) No mistake (5) 1018, 1024, 1022, 1024
How to find the mistakes?The given parameters that will guide to us detect the error in the sequence are
1. 114, 118, 112, 116, 121, 125, 129, 133
The sequence is in Arithmetic progress with a common difference of 4
The correct sequence should be
114,118,112,116,120,124,128,132
2. The given sequence is 2155,2160,2165,2170,2175,2180,2190,2200
The sequence is also in Arithmetic Progression with a difference of 5
The correct answer is 2155,2160,2165,2170,2175,2180,2185,2190
3. The given sequence is 597,598,599,601,610,611,612,613
The sequence is not correct,
The common difference between the terms is 1
The correct answer is 597,598,599,600,601,602,603,604
4. The sequence is 218,225,232,239,246,253,260,267
The common difference of the AP is 7
You can notice that there is no mistakes
5. The given sequence is 1018,1024,1022,1024,1030,1032,1034
The is a mistake in the sequence.
The common difference is 2
The correct sequence should be 1020,1022,1024,1026,1028,1030,1032,1034
In conclusion, there are some errors as corrected in the sequence above
Learn more about sequence on https://brainly.com/question/21961097
#SPJ1
Which of the following factors does NOT control the stability of a slope?
the angle of repose for intact bedrock
whether the slope is rock or soil
the amount of water in the soil
the orientation of fractures, cleavage, and bedding
Answers
The factor that does NOT control the stability of a slope is the angle of repose for intact bedrock. The angle of repose refers to the steepest angle at which a pile of loose material remains stable without sliding. It is mainly applicable to loose materials like soil and granular substances, not intact bedrock.
Bedrock stability depends on factors such as its strength, fracturing, and geological properties, rather than the angle of repose. Factors that control the stability of a slope include whether the slope is rock or soil. Rock slopes tend to be more stable than soil slopes due to the cohesive nature of intact rock.
The amount of water in the soil also affects slope stability, as excessive water can increase pore pressure and reduce the shear strength of the soil, leading to slope failure. Additionally, the orientation of fractures, cleavage, and bedding in the rock can influence slope stability by creating planes of weakness or strength.
To summarize, while the angle of repose is a significant factor in slope stability, it is not applicable to intact bedrock. The stability of a slope is influenced by the type of material (rock or soil), the presence of water, and the orientation of fractures and bedding.
know more about Bedrock.
https://brainly.com/question/2948854
#SPJ11
a high school theater club has 40 student, 6 of whom are left handed. two student will be selected at random, one at a time without replacement. what is the pobability that the 2 student selected will both be left-handed/
Answers
1.92% is the probability .
Describe probability using an example?
By dividing the number of preferable possibilities by the total number of potential outcomes, probability, which measures the likelihood that an event will occur, is obtained. The most basic illustration is a coin toss. There are only two outcomes that can occur when you flip a coin: either heads or tails.The probability of an event is the ratio of the size of the event space to the size of the sample space.
The size of the sample space is the total number of possible outcomes
The event space is the number of outcomes in the event you are interested in.
so
Let
x------> size of the event space
y-----> size of the sample space
so
P = x/y
Find out the probability that the first student selected will be left-handed
we have
x = 6
y = 40
substitute
P = 6/40
Simplify
P = 3/20
the probability that the second student selected will be left-handed
we have
x = 6 - 1 = 4
y = 40 -1 = 39
substitute
P = 5/39
the probability that the 2 students selected will both be left-handed
Multiply the probabilities
P = 3/20(5/39) = 15/780
Convert to percentage
Multiply by 100
15/780 * 100 = 1.92%
Lean more about probability.
brainly.com/question/11234923
#SPJ4
There are 4 grams of sugar in 1⁄2 of a liter of a new sports drink. How much sugar is in 3⁄4 of a liter of the sports drink?
Answers
Answer:
6 grams of sugar in 3/4 liter.
Explanation:
Recall that two 1/4 portions is equal to 1/2. So if 1/2 liter has 4 grams, 1/4 liter will have 2 grams of sugar.
Every 1/4 liter will have 2 grams of sugar.
Therefore, 3/4 liter will have 3 times as much sugar as 1/4 liter. The amount of sugar in 3/4 liter will be 3 times 2 grams or 6 grams of sugar in 3/4 liter
what is the rate of change of the surface area of the prism at that instant (in square kilometers per minute)?
Answers
The surface area, A, is changing at a rate of 288 km/min decreasing.
Given,
Base length, l = 6 km
Height, h = 10 km
dl/dt = -9 km/min
dh/dt = 12 km/min
Surface area of a prism, A = 2 × (lw + lh + wh)
For a square prism,
Length, l = width, w = 6km
A = 2 × (l² + lh + lh)
= 2(l²) + 4lh
A = 2(l²) + 4 lh
= 2 × (l² + 2lh)
dA/dt = 2 × (2I × dI/dt + 0 × dh/dt + 2 × 2h × dl/dt + 2l × dh/dt)
dA/dt = 2 × (2l × dl/dt + 0 + 2 × 2h × dl/dt + 2l × dh/dt)
= 2 × (2(6) × (-9) + 2(10) × (-9) + 2(6) × (12))
= 2 × (- 108 + -180 + 144)
= 2 × -144
= -288 km/min
The rate of change of the surface area, A is decreasing by 288 km/min.
Learn more about rate of change of surface area here;
https://brainly.com/question/15407859
#SPJ4
Question is incomplete. Completed question is given below;
The length s(t)s(t)s, (, t, )of the side of the base of a square prism is decreasing at a rate of 9 kilometers per minute and the height h(t)h(t)h, (, t, )of the prism is increasing at a rate of 12 kilometers per minute. At a certain instant t_0t 0 t, start subscript, 0, end subscript, the base's side is 6 kilometers and the height is 10 kilometers. What is the rate of change of the surface area A(t)A(t)A, (, t, )of the prism at that instant?
5. (10 points) Using the method of Lagrange Multipliers, find the absolute maximum and minimum values of \( f(x, y)=2 x-3 y \) subject to the constraint \( x^{2}+y^{2}=1 \).
Answers
The absolute maximum value of f(x, y) is √13, and the absolute minimum value is -√13.
To find the absolute maximum and minimum values of the function f(x, y) = 2x - 3y subject to the constraint \(x^{2}\) + \(y^{2}\) = 1, we can use the method of Lagrange multipliers. Let's set up the following system of equations:
∇f = λ∇g
g(x, y) = \(x^{2}\) + \(y^{2}\) - 1
where ∇f and ∇g are the gradients of f and g, respectively, and λ is the Lagrange multiplier.
The partial derivatives are:
∂f/∂x = 2
∂f/∂y = -3
∂g/∂x = 2x
∂g/∂y = 2y
Setting up the system of equations:
2 = λ(2x)
-3 = λ(2y)
\(x^{2}\) + \(y^{2}\) = 1
From the first equation, we have x = λ.
From the second equation, we have y = -3λ/2.
Substituting these values into the third equation:
(λ\()^{2}\) + (-3λ/2\()^{2}\) = 1
(λ\()^{2}\) + (9(λ\()^{2}\) /4) = 1
(13(λ\()^{2}\) )/4 = 1
(λ\()^{2}\) = 4/13
λ = ±2/√13
Now, we can find the corresponding values of x and y:
For λ = 2/√13:
x = 2/√13
y = -3(2/√13)/2 = -3/√13
For λ = -2/√13:
x = -2/√13
y = -3(-2/√13)/2 = 3/√13
Now, we evaluate the function f(x, y) at these points:
f(2/√13, -3/√13) = 2(2/√13) - 3(-3/√13) = (4 + 9)/√13 = 13/√13 = √13
f(-2/√13, 3/√13) = 2(-2/√13) - 3(3/√13) = (-4 - 9)/√13 = -13/√13 = -√13
Therefore, the absolute maximum value of f(x, y) = 2x - 3y subject to the constraint \(x^{2}\) + \(y^{2}\) = 1 is √13, and the absolute minimum value is -√13.
To learn more about absolute maximum here:
https://brainly.com/question/31136513
#SPJ4
Please help!!! Will give brainliest to the first correct answer!

Answers
Answer:
a. (-4,8)
Step-by-step explanation:
the two lines intersect at this point