Answers
Answer: 264 cubic centimeters
8*8*1=64
8*5*5=200
200+64=264
Related Questions
a pond contains 100 fish, of which 30 are carp. if 20 fish are caught, what are the mean and variance of the number of carp among the 20? what assumptions are you making?
Answers
A pond contains 100 fish, of which 30 are carp. if 20 fish are caught, what are the mean and variance of the number of carp among the 20. This Statement is based on the assumption that : X follows hyper-geometric distribution with the given information.
According to the Question:
Total fish = 100
Carp = 30
Number of fish caught = 20
Now,
The random variable X follows hyper-geometric distribution.
Mean = 30 *20 / 100
= 600/100 = 6
Therefore,
Variance = 30*20/100 * ((20-1)*(30-1)/100-1 + 1-30*20/100)
⇒ Variance = 600/100 * 56/99
⇒ Variance = 112/33
⇒ variance = 3.1111 ≈ 3.12
Assumptions:
Is that X follows hyper-geometric distribution with the given information.
Hyper - Geometric Distribution:
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that yields n draws without replacement for k successes (if the drawn object has a particular property). random draw). From a finite population of size N containing exactly K objects with this property, each draw either succeeds or fails. In contrast, the binomial distribution describes the probability of k successes in n draws with replacement.
Learn More about Variance:
https://brainly.com/question/29505178
#SPJ4
*WILL MARK BRAINLIEST*
given the inequality 4x-y<=k-6, there is a minimum value of k in order for the point (5,0) to be part of a solution. what is the minimum value?
Answers
Answer:
26
Step-by-step explanation:
since the question asks for a value of k where the point (5, 0) is part of a solution, plug 5 into the x value and 0 into the y value:
4x-y<=k-6
4(5)-0<=k-6
20-0<=k-6
20<=k-6
26<=k
In this case, k can be equal to any number that is greater than or equal to 26 for the point (5, 0) to be a solution, but the question asks for the minimum value of k, meaning the smallest value. since the question asks for the smallest value, the answer we're looking for is 26.
lmk if this is wrong, hope it helps!!
Part A )a painter leans a ladder up against a building. The base of the ladder is placed 7 feet from the building to reach a height of 24 feet. How long is the ladder
Part B) The painter uses the same ladder from part A, but now needs to reach a height of 19 feet.How far away does the base of the ladder need to be placed from the building?

Answers
Answer:
Part A). 25 feet
Part B). 16.25 feet
Step-by-step explanation:
Part A). By applying Pythagoras theorem in ΔABC,
AC² = AB² + BC²
AC² = (24)² + 7²
AC² = 576 + 49
AC = √625
= 25 feet
Part B). By applying Pythagoras theorem in ΔABC,
AC² = AB² + BC²
(25)² = (19)² + x²
625 = 361 + x²
x² = 625 - 361
x = √264
x = 16.25 feet

solve for x. 2/3x = -2/3
Answers
Answer:
solve for x. 2/3x = -2/3. X=1
Step by step for 7,9, 11. EVEN IF U CANT DO ALL, u can help with 1 or 2. Ill mark brainly.

Answers
Answer:
7) \(4 \ log_3(x) - 4 \ log_3(y)\)
9) \(5log_4(7) - 5log_4(12)\)
11) \(5log_5 \ (x) - log_5 \ (y)\)
Step-by-step explanation:
\(log_3 (\frac{x}{y})^{4}\)
----------------------------------------------------------------------------------------------------
Use Logarithm of a Quotient which states
\(log_b \frac{M}{N} = log_b M-log_bN\)
And also use Logarithm of a Power which states
\(log_b\ M^{n} = n\log_bM\)
----------------------------------------------------------------------------------------------------
So using these two properties,
7. \(4 \ log_3(x) - 4 \ log_3(y)\)
----------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------
For #9, use the same logarithm propertied
\(log_4(\frac{7}{12})^5 = 5log_4(7) - 5log_4(12)\)
----------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------
#11 is also the same concept
\(log_5\ \frac{x^5}{y} = 5log_5 \ (x) - log_5 \ (y)\)
It is not - 5 log5(y) since only x is to the power of 5 not y
----------------------------------------------------------------------------------------------------
Hope this is what you were looking for and helps you! Have a nice day/night :)
If x = 18, evaluate the following expression:
12 + 3

Answers
30
Explanation
12+18=30
Before sending track and field athletes to the Olympics, the U.S. holds a qualifying meet.
The upper box plot shows the top
12
1212 men's long jumpers at the U.S. qualifying meet. The lower box plot shows the distances (in meters) achieved in the men's long jump at the
2012
20122012 Olympic games.
2 horizontal boxplots titled U.S. Qualifier and Olympics are graphed on the same horizontal axis, labeled Distance, in meters. The boxplot titled U.S. Qualifier has a left whisker which extends from 7.68 to 7.7. The box extends from 7.7 to 7.89 and is divided into 2 parts by a vertical line segment at 7.74. The right whisker extends from 7.9 to 7.99. The boxplot titled Olympics has a left whisker which extends from 7.7 to 7.83. The box extends from 7.83 to 8.12 and is divided into 2 parts by a vertical line segment at 8.04. The right whisker extends from 8.12 to 8.31. All values estimated.
Which pieces of information can be gathered from these box plots?
Choose all answers that apply:
Choose all answers that apply:
(Choice A) The Olympic jumps were farther on average than the U.S. qualifier jumps.
A
The Olympic jumps were farther on average than the U.S. qualifier jumps.
(Choice B) All of the Olympic jumps were farther than all of the U.S. qualifier jumps.
B
All of the Olympic jumps were farther than all of the U.S. qualifier jumps.
(Choice C) The Olympic jumps vary noticeably more than the U.S. qualifier jumps.
C
The Olympic jumps vary noticeably more than the U.S. qualifier jumps.
(Choice D) None of the above
D
None of the above
Answers
The pieces of information that the box plots on the distances show include:
A. The Olympic jumps were farther on average than the U.S. qualifier jumps.C. The Olympic jumps vary noticeably more than the U.S. qualifier jumps.What does the box plot show ?The box plot on the the distances (in meters) achieved in the men's long jump first shows that due to the fact that the length of the box for the Olympics was longer, the Olympic jumpers were farther on average than the U.S. qualifier jumps.
The box plot also shows that due to the whisker and the box for the Olympics being longer than the U.S. qualifier, there was more variance with the Olympic jumps.
Find out more on box plots at https://brainly.com/question/30652189
#SPJ1

Validation of the model and answering the question "what are my options" occur in the ___ phase of the IDC.
A. choice
B. design
C. intelligence
D. implantation
Answers
Validation of the model and answering the question "what are my options" occur in the design phase of the IDC (Intelligence, Design, and Choice) framework.
The IDC framework is a decision-making process that consists of three phases: Intelligence, Design, and Choice. Each phase corresponds to a specific set of activities and objectives.
In the intelligence phase, the focus is on gathering information, identifying the problem or decision to be made, and understanding the factors and variables involved. This phase involves data collection, analysis, and exploration to gain insights and knowledge about the problem domain.
In the design phase, the emphasis is on developing and evaluating potential options or solutions to address the problem or decision at hand. This phase involves creating models, prototypes, or simulations to represent the problem and exploring different alternatives.
Validation of the model is an important aspect of this phase to ensure that the proposed solutions align with the problem requirements and objectives.
The question "what are my options" is a fundamental question that arises during the design phase. It implies the exploration and generation of various possible choices or solutions that can be evaluated and compared.
Therefore, the design phase of the IDC framework encompasses the activities of validating the model and answering the question "what are my options." It involves refining and testing potential solutions to make informed decisions in the subsequent choice phase.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
Jack is building a rectangular fence for his ferret. He has 20 feet of fencing and wants the short side of the fence to be 72 feet. How long will the other side of the fence be? write the answer in decimal form. The long side will be feet.
Answers
Answer
There is a contradiction in the question. We are told there is only 20 feet of fencing, but the short side is to be 72 feet. I will answer using the assumption that the 20 feet was supposed to be 200 feet.
The remaining side would be 28 feet.
Step-by-step explanation:
The perimeter of the fence can be no larger than the available fencing, 200 ft. Will will assume all of the fencing is to be used.
Let L and W stand for the feet of fencing for the Length and Width, respectively.
Perimeter = 2L + 2W
Let L be the short side:
L = 72 feet
200 ft= 2(72 feet) + 2W
200 feet = 144 feet + 2W
2W = 56 feet
W = 28 feet
Answer:
6.5 feet
Step-by-step explanation:
You want to know the length of the other side of a rectangular fence if the perimeter is 20 feet and one side is 7/2 feet.
PerimeterThe formula for the perimeter of a rectangle is ...
P = 2(L +W)
Filling in the given values, we can find the missing length:
20 = 2(L +7/2) . . . . use the given values
10 = L +7/2 . . . . . . divide by 2
13/2 = L = 6.5 . . . . subtract 7/2
The long side will be 6.5 feet.
You can read more about the ferret fence here:
https://brainly.com/question/8955475
<95141404393>
what is the probability that the sum of two randomly chosen integers between 20 and 40 inclusive is even (if the possibility of the two integers being equal is allowed)?
Answers
We have that, the probability is given by 221/441.
How do we calculate the probability?The probability of the sum of two randomly chosen integers between 20 and 40 inclusive being even can be calculated using the formula: P(Even) = P(Even + Even) + P(Odd + Odd) = (P(Even))^2 + (P(Odd))^2
First, we need to determine the probability of choosing an even integer and the probability of choosing an odd integer. There are a total of 21 integers between 20 and 40 inclusive (40 - 20 + 1 = 21), and 11 of them are even (20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40) while 10 of them are odd (21, 23, 25, 27, 29, 31, 33, 35, 37, 39).
Therefore, P(Even) = 11/21 and P(Odd) = 10/21.
Plugging these values into the formula, we get:
P(Even) = (11/21)^2 + (10/21)^2 = 121/441 + 100/441 = 221/441
So the probability that the sum of two randomly chosen integers between 20 and 40 inclusive is even is 221/441.
Read more; https://brainly.com/question/24756209
#SPJ11
A quadratic function y=f(x) is plotted on a graph and the vertex of the resulting parabola is (3,−5). What is the vertex of the function defined as g(x)=−f(x−2)?
Answers
Answer:
\((5,5)\)
Step-by-step explanation:
\(f(x-2) \text{ Shifts graph right 2}\)
\(\text{Vertex is now } (5, -5)\)
\(-f(x-2) \text{ Reflects graph across x-axis}\)
\(\text{Vertex is now } (5,5)\)
What is the mean of these number 2.45 3.12 2.8
Answers
Answer:
2.79
Step-by-step explanation:
2.45 + 3.12 + 2.8 = 8.37
2.79 ÷ 3 = 2.79
Answer:
4.185
Step-by-step explanation:
To get the mean you add all of the numbers up and with the number that you get you divide it by 2.
You add 2.45, 3.12, and 2.8.
You get 8.37 and then you divide by 2 and get 4.185.
Hope this helps!! :)
What is the distance between (-9, -6) and (-2,-2)?
Answers
Answer:
To find this we use the distance formula.
Square root of (-2 + 9)^2 + (-2 + 6)^2
square root of 49 + 16
square root of 65
8.0622577483
Step-by-step explanation:

PLEASE HELP!!
What is the range of y=x+3^2?
A: all real numbers
B:{3^2}
C: all real numbers except 9.
D:{1,3,9}
Answers
Answer:
A
Step-by-step explanation:
What is the common difference for the arithmetic sequence?
3.2, 5, 6.8, 8.6, 10.4
help me please!
Answers
Answer:
the difference is 1.8
Step-by-step explanation:
5-3.2=1.8
6.8-5=1.8
8.6-6.8=1.8
ect
in pe class you are picking teams for a basketball game. there will be a red team and a blue team. there are 13 students in the class. how many different ways can the teams be picked if the teacher stipulates that the two best players can not be on the same team?
Answers
There are 49,152 possible ways to pick teams for a basketball game in a PE class with 13 students if the two best players cannot be on the same team.
If we denote the two best players as A and B, then we can split the problem into two cases
A is on the red team: In this case, B can be on any of the remaining 12 students, and the other 11 students can be split between the red and blue teams in any way. Therefore, there are 12 × 2^11 = 24,576 possible team combinations.
A is on the blue team: This case is identical to case 1, so there are also 24,576 possible team combinations.
Therefore, the total number of possible team combinations where A and B are not on the same team is
24,576 + 24,576 = 49,152.
Learn more about combination here
brainly.com/question/28720645
#SPJ4
6 feet
4.5 feet
3 feet
The rectangles are similar. What is the length in feet of the smaller
rectangle?
A 4
B. 4.2
C. 5
D. 5.5
Answers
Answer:
140
Step-by-step explanation:
(7/4) (80) =140 this is the answer for you.
The perpendicular bisector of the line segment connecting the points $(-3,8)$ and $(-5,4)$ has an equation of the form $y
Answers
The equation of the perpendicular bisector is of the form \($y = mx + b$\), where \($m = -\frac{1}{2}$\) and \($b = 4$\).
The equation of the perpendicular bisector of the line segment connecting the points \($(-3,8)$\) and \($(-5,4)$\)has the form \($y = mx + b$\).
To find the equation of the perpendicular bisector, we first need to find the midpoint of the line segment connecting the two points. The midpoint formula is given by:
Midpoint \(= $ \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) $\)
Using the given points $(-3,8)$ and $(-5,4)$, we can calculate the midpoint as follows:
Midpoint\(= $ \left( \frac{-3 + (-5)}{2}, \frac{8 + 4}{2} \right) = (-4, 6) $\)
Now that we have the midpoint, we need to determine the slope of the line segment connecting the two points. The slope formula is given by:
Slope \(= $ \frac{y_2 - y_1}{x_2 - x_1} $\)
Using the coordinates $(-3,8)$ and $(-5,4)$, the slope can be calculated as follows:
Slope \(= $ \frac{4 - 8}{-5 - (-3)} = \frac{-4}{-2} = 2 $\)
The slope of the perpendicular bisector is the negative reciprocal of the slope of the line segment. Therefore, the slope of the perpendicular bisector is $-\frac{1}{2}$.
Now, using the midpoint $(-4, 6)$ and the slope $-\frac{1}{2}$, we can find the equation of the perpendicular bisector by substituting these values into the slope-intercept form equation $y = mx + b$:
$6 = -\frac{1}{2} \cdot (-4) + b$
Simplifying the equation:
$6 = 2 + b$
$b = 6 - 2 = 4$
Therefore, the equation of the perpendicular bisector of the line segment connecting the points $(-3,8)$ and $(-5,4)$ is:
$y = -\frac{1}{2}x + 4$
Hence, the equation of the perpendicular bisector is of the form $y = mx + b$, where $m = -\frac{1}{2}$ and $b = 4$.
Learn more about bisector here
https://brainly.com/question/30716032
#SPJ11
Find 6, 750 - 240.
what is 6,759 divided by 240
Answers
Answer:
40
Step-by-step explanation:
Step 1:
Start by setting it up with the divisor 6 on the left side and the dividend 240 on the right side.
Step 2:
The divisor (6) goes into the first digit of the dividend (2), 0 time(s). Therefore, put 0 on top.
Step 3:
Multiply the divisor by the result in the previous step (6 x 0 = 0) and write that answer below the dividend.
Step 4:
Subtract the result in the previous step from the first digit of the dividend (2 - 0 = 2) and write the answer below.
Step 5:
Move down the 2nd digit of the dividend (4).
Step 6:
The divisor (6) goes into the bottom number (24), 4 time(s). Therefore, put 4 on top.
Step 7:
Multiply the divisor by the result in the previous step (6 x 4 = 24) and write that answer at the bottom.
Step 8:
Subtract the result in the previous step from the number written above it. (24 - 24 = 0) and write the answer at the bottom.
Step 9:
Move down the last digit of the dividend (0).
Step 10:
The divisor (6) goes into the bottom number (0), 0 time(s). Therefore put 0 on top.
Step 11:
Multiply the divisor by the result in the previous step (6 x 0 = 0) and write the answer at the bottom.
Step 12:
Subtract the result in the previous step from the number written above it. (0 - 0 = 0) and write the answer at the bottom.
Hope this helps!
What is 73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73=
Answers
Answer:
1533
Step-by-step explanation:
73x21= 1533
Answer:
73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73+73
=73x21=1533
Step-by-step explanation:
"
A particle is moving according to the position function \( s(t)=(4 t+1)^{3 / 2} \), where \( s(t) \) is measured in centimeters and \( t \) in seconds. Find the acceleration of the particle at \( t=2 seconds. find
"
Answers
The acceleration of the particle at \(t = 2\) seconds is \(4\) cm/s².
To find the acceleration of the particle at \(t = 2\) seconds, we need to differentiate the position function twice with respect to time. First, let's differentiate the position function \(s(t)\) once to find the velocity function \(v(t)\). Using the chain rule, we have:
\(\(v(t) = \frac{d}{dt}[(4t+1)^{3/2}]\)\)
To simplify the differentiation, we can rewrite the function as\(\(v(t) = (4t+1)^{3/2}\)\) . Applying the power rule, the derivative becomes:
\(\(v(t) = \frac{3}{2}(4t+1)^{1/2} \cdot 4\)\)
Simplifying further, we have:
\(\(v(t) = 6(4t+1)^{1/2}\)\)
Next, we differentiate the velocity function \(v(t)\) to find the acceleration function \(a(t)\):
\(\(a(t) = \frac{d}{dt}[6(4t+1)^{1/2}]\)\)
Using the power rule again, we get:
\(\(a(t) = 6 \cdot \frac{1}{2}(4t+1)^{-1/2} \cdot 4\)\)
Simplifying further, we have:
\(\(a(t) = 12(4t+1)^{-1/2}\)\)
Now we can find the acceleration at \(t = 2\) seconds by substituting \(t = 2\) into the acceleration function:
\(\(a(2) = 12(4 \cdot 2 + 1)^{-1/2}\)\)
\(\(a(2) = 12(9)^{-1/2}\)\)
Simplifying the expression, we have:
\(\(a(2) = \frac{12}{3} = 4\) cm/s²\)
Therefore, the acceleration of the particle at \(t = 2\) seconds is \(4\) cm/s².
To know more about acceleration refer here:
https://brainly.com/question/12550364
#SPJ11
Suppose there are two producers in a market with the following supply functions. Supply 1: P=6+0.7Q Supply 2:P=16+0.6Q When the price is [Answer], the total quantity supplied is 250. (In decimal numbers, with two decimal places, please.) Answer:
Answers
The price at which the total quantity supplied is 250 is $11.58.
In order to find the price at which the total quantity supplied is 250, we need to equate the total quantity supplied by both producers (Supply 1 and Supply 2) and solve for the price.
Supply 1: P = 6 + 0.7Q
Supply 2: P = 16 + 0.6Q
To find the equilibrium price, we set the total quantity supplied equal to 250:
0.7Q + 0.6Q = 250
1.3Q = 250
Q = 250 / 1.3 ≈ 192.31
Now that we have the quantity, we can substitute it back into either supply function to find the price. Let's use Supply 1:
P = 6 + 0.7Q
P = 6 + 0.7 * 192.31
P ≈ 6 + 134.62
P ≈ 140.62
Therefore, the price at which the total quantity supplied is 250 is approximately $11.58.
Learn more about Equilibrium price
brainly.com/question/29099220
#SPJ11
Drag the tiles to the correct boxes to complete the pairs.
Match each solution to the equation it solves.
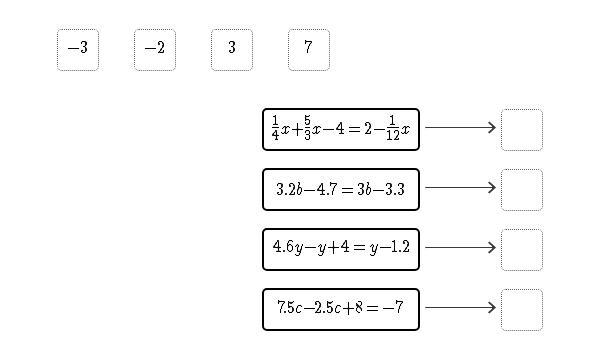
Answers
Answer:
the first one is 3
the second one is 7
the third one is -2
and the last one is -3
Step-by-step explanation:
The equation is matched with its solutions below;
1/4x + 5/3x - 4 = 2 - 1/12x; x = 33.2b - 4.7 = 3b - 3.3; b = 74.6y - y + 4 = y - 1.2; y = -27.5c - 2.5c + 8 = - 7; c = -3What is the solution to the equation?1/4x + 5/3x - 4 = 2 - 1/12x
combine like terms
1/4x + 5/3x + 1/12x = 2 + 4
(3x+20x+x) / 12 = 6
24/12x = 6
2x = 6
Divide both sides by 2
x = 6/2
x = 3
3.2b - 4.7 = 3b - 3.3
combine like terms
3.2b - 3b = -3.3 + 4.7
0.2b = 1.4
divide both sides by 0.2
b = 1.4 / 0.2
b = 7
4.6y - y + 4 = y - 1.2
combine like terms
4.6y - y - y = - 1.2 - 4
2.6y = - 5.2
divide both sides by 2.6
y = -5.2 / 2.6
y = -2
7.5c - 2.5c + 8 = - 7
5c = -7 - 8
5c = -15
divide both sides by 5
c = -15/5
c = -3
Read more on equation:
https://brainly.com/question/29174899
#SPJ2
Help I’m literally confused on these
Perpendicular Bisector Theorem

Answers
Answer:
UV = 10
Step-by-step explanation:
VX is a perpendicular bisector of the base UW , then Δ UVW is isosceles with the 2 legs being congruent , that is
UV = VW = 10
Share 35 sweets in the ratio 4:3
Answers
number sweet is 35
we divided ratio =4x:3x
total = 4x+3x
7x= 35
= 35/7
x= 5
1 st part will be 4x = 4*5= 20 sweets.
2 nd part will be 3x = 3*5= 15sweets
impartind numarul natural x la numarul natural y obtinem catul 3 si restul 19
A. Calculati 2•x-6•y+3
B. Aratati ca c+y>95
C. Aflati x si y,daca x-y<61
Answers
Answer:
ok
Step-by-step explanation:
Consider tossing a fair coin n times. For k = 1,...,n, define the events Ak = {"the first k tosses yield only head"}. (a) You want to model this experiment as a Laplace experiment. Find a suitable sample space and compute P(Ax). (b) Describe in words the event Ax-1 Ak. What is the probability of this event?
Answers
a) The probability of event Ak is P(Ak) = \((1/2)^k * (1/2)^{n-k}\) = (1/2)ⁿ. b) The probability of the event Ax-1 Ak is (1/2)^k.
(a) To model the experiment as a Laplace experiment, we can define the sample space as the set of all possible outcomes of tossing a fair coin n times. Each outcome can be represented as a sequence of n coin tosses, where each toss can result in either a head (H) or a tail (T). Therefore, the sample space can be written as:
Ω = {HHHH...HHH, HHHH...HHT, HHHH...HTH, ..., TTTT...TTT}
Since the coin is fair, the probability of obtaining a head in each toss is 1/2, and the probability of obtaining a tail is also 1/2. Thus, each outcome in the sample space is equally likely, and the probability of each outcome is 1/2^n.
For the event Ak, "the first k tosses yield only heads," there is only one outcome that satisfies this event, which is the sequence of k heads followed by (n-k) tails:
Ak = {HH...HTTT...TT}
The probability of this event, P(Ak), can be calculated by considering that each coin toss is independent. Since the probability of obtaining a head in each toss is 1/2, the probability of getting k heads in k tosses is (1/2)^k. The probability of getting (n-k) tails in (n-k) tosses is also (1/2)^(n-k).
(b) The event Ax-1 Ak represents the situation where the first (k-1) tosses yield only heads, and then the kth toss also yields a head. In other words, it means that we obtain k consecutive heads in the first k tosses. This event can be represented as:
Ax-1 Ak = {HH...HH}
The probability of this event, P(Ax-1 Ak), can be calculated in a similar manner as above. Since the first (k-1) tosses yielding heads and the kth toss yielding a head are independent events, the probability is:
P(Ax-1 Ak) = (1/2).
To know more about probability:
https://brainly.com/question/31828911
#SPJ11
1 Alex uses 1 yards of ribbon to decorate each picture frame. He wants to decorate 6 picture frames 3 • Determine how many yards of ribbon Alex needs to decorate the picture frames. • Show your work or explain your answer.
Answers
Part A:
Jessica has 1/2 yard of ribbon
1/2 yd = 0.5 yd
She uses an equal amount of ribbon to decorate 3 picture frames.
So, basically we need to divide the total amount of ribbon by 3:
0.5 yd/ 3 = 1/6 yd
Part B:
Let's first express the mixed number as a fraction:
1 1/3 yd = 4/3 yd
Alex uses the same amount of ribbon for each frame. And he needs to decorate 6, Hence:
We multiply the amount of ribbon in each frame, by the total of frames:
4/3 yd * 6 = 8 yd
a full-cut round brilliant diamond with a 6.50 mm girdle diameter weighs about
Answers
That a full cut round brilliant diamond with a 6.50 mm girdle diameter typically weighs around 1.00 carat.
carat weight is determined by a combination of a diamond's size and density. A diamond's size is measured by its diameter, which is the distance across the widest part of the diamond, known as the girdle. Therefore, a diamond with a larger girdle diameter will generally weigh more than a diamond with a smaller diameter, assuming all other factors are equal.
the weight of a diamond can be estimated based on its girdle diameter, and a full-cut round brilliant diamond with a 6.50 mm girdle diameter typically weighs around 1.00 carat. However, it's important to note that other factors, such as depth, cut, and clarity, can also affect a diamond's weight and value.
To know more about diamond, visit:
https://brainly.com/question/29775108
#SPJ11
can anyone do this quickly?

Answers
Answer:
4th option (x = 60)
Step-by-step explanation:
This is isosceles triangle so the angles are the same. Think of this as an mirror. AE is the same as BE so you can assume angle ABE is 30 degrees.
30+30=60
180-60=120
So angle AEB is 120.
That is supplementary angle so the other side must be 180-120=60.
So, the middle smaller triangle is isosceles as well, so BED and BDE are both 60.
60+60=120, 180-120=60
So angle x = 60
