Answers
For the nut question multiply the cost of the almonds by 2 then subtract that from total of everything then take the new total and divide by 4 for cost of 1kg cashews.A:$3.63
Related Questions
Please help explanation if possible

Answers
Answer:
(x,y) —> (–1 ,1)
I hope I helped you ^_^
Pls show your work thank you will mark the Brainliest

Answers
Option a) The zeros are -10 and 2 because the factors of g are\((x+10)\) and \((x-2)\) of the given equation g(x).
What is the equation?In mathematics, an equation is a statement that asserts the equality of two expressions, which are typically represented by letters, numbers, and symbols. In algebra, the meaning of an equation is a mathematical statement that indicates that two mathematical expressions are equivalent. When an equation contains two variables, both of degree one, it is recognized as a linear equation in two variables.
Factors refer to the things or variables that can influence a situation or outcome. Factors can be numerous and can vary depending on the context.
According to the given information,
We can solve for x by setting g(x) equal to zero and using the quadratic formula:
\(g(x) = x^2 - 8x - 20 = 0\)
Using the quadratic formula:
\(x = (-(-8)\) ± \(\sqrt((-8)^2 - 4(1)(-20))) / 2(1)\)
\(x = (8\) ± \(\sqrt(64 + 80)) / 2\)
\(x = (8 +}/{-} \sqrt(144)) / 2\)
\(x = (8 \frac{+}{-} 12) / 2\)
So, \(x = 10 or x = -2.\)
Therefore, the solutions for \(g(x) = x^2 - 8x - 20\)are\(x = 10 and x = -2.\)
To know more about equation visit:
brainly.com/question/12788590
#SPJ1
works correctly at the 445 gram setting. based on a 27 bag sample where the mean is 448 grams and the standard deviation is 19, is there sufficient evidence at the 0.025 level that the bags are overfilled?
Answers
Based on the given information, there is not enough evidence at the 0.025 level to conclude that the bags are overfilled. This can be answered by the concept of Standard deviation.
To determine whether there is enough evidence to conclude that the bags are overfilled, we need to perform a hypothesis test.
Let the null hypothesis be that the bags are not overfilled, and the alternative hypothesis be that the bags are overfilled. We can set the significance level at 0.025.
We will perform a one-sample t-test since we have a small sample size and the population standard deviation is unknown. Using the formula for the t-test statistic, we obtain a t-value of 1.58. The critical t-value for a two-tailed test with 26 degrees of freedom (n-1) and a significance level of 0.025 is 2.479. Since 1.58 < 2.479, we fail to reject the null hypothesis.
Therefore, there is not enough evidence at the 0.025 level to conclude that the bags are overfilled.
To learn more about Standard deviation here:
brainly.com/question/23907081#
#SPJ11
What’s the rise over run pleas???

Answers
9514 1404 393
Answer:
-1/5
Step-by-step explanation:
To find the ratio of rise to run on a graph, it is convenient to start by looking for points where the graph crosses the intersection of grid lines. This lets you read the exact coordinates of the points, without any guessing.
In the attachment, the grid crossings we chose are circled.
The "rise" is the vertical distance between the points. If the right point is lower, the "rise" is negative.
The "run" is the horizontal distance between the points.
The reason for choosing grid crossings is that it then becomes fairly easy to count the grid lines between the points, vertically and horizontally.
On this graph, the "rise" is -1 for a "run" of 5. Then the slope, or ratio of rise to run, is ...
m = rise/run = -1/5 . . . . . . slope of the line

suppose the random variable x comes from some distribution with a mean \mu and standard deviation \sigma. for a sufficiently large sample size, the sampling distribution of the sample mean is:
Answers
Approximately normal with a mean equal to \mu and a standard deviation equal to \frac{\sigma}{\sqrt{n}}, where n is the sample size. This result is known as the Central Limit Theorem.
According to the Central Limit Theorem, as the sample size increases, the distribution of the sample mean becomes increasingly close to a normal distribution, regardless of the shape of the original distribution.
The Central Limit Theorem is a fundamental result in probability and statistics that states that the distribution of the sum (or average) of a large number of independent, identically distributed random variables approaches a normal distribution.
This result is particularly useful because it provides a way to make probabilistic statements about the distribution of a sample mean, even if the distribution of the underlying data is unknown.
You can read more about The Central Limit Theorem at https://brainly.com/question/30557295#:
#SPJ4
The number of Miles a car can be driven is proportional to the number of gallons of gasoline at uses. The car can be driven 14 miles per one and a half gallon of gasoline used. What is the constant of proportionality for the relationship between miles driven and gallons of gasoline?
Answers
Answer:
k = 9.34
Step-by-step explanation:
The number of Miles a car can be driven is proportional to the number of gallons of gasoline it uses.
x ∝ g
x = kg ....(1)
k is constant of proportionality, x is no of miles and g is no of gallons
The car can be driven 14 miles per one and a half gallon of gasoline used.
Here x = 14 and g = \(1\dfrac{1}{2}=\dfrac{3}{2}\)
Put values in equation (1) to find k.
\(k=\dfrac{14}{\dfrac{3}{2}}\\\\x=9.34\)
Hence, the value of constant of proportionality is 9.34.
calculate the taylor polynomials 2 and 3 centered at =0 for the function ()=16tan().
Answers
Taylor polynomials of degree 2 and 3 centered at x = 0 for the function f(x) = 16tan(x) are:
P2(x) = 16x + 8x^2
P3(x) = 16x + 8x^2
To find the Taylor polynomials centered at x = 0 for the function f(x) = 16tan(x), we can use the Taylor series expansion for the tangent function and truncate it to the desired degree.
The Taylor series expansion for tangent function is:
tan(x) = x + (1/3)x^3 + (2/15)x^5 + (17/315)x^7 + ...
Using this expansion, we can find the Taylor polynomials of degree 2 and 3 centered at x = 0:
Degree 2 Taylor polynomial:
P2(x) = f(0) + f'(0)(x - 0) + (1/2!)f''(0)(x - 0)^2
= 16tan(0) + 16sec^2(0)(x - 0) + (1/2!)16sec^2(0)(x - 0)^2
= 0 + 16x + 8x^2
Degree 3 Taylor polynomial:
P3(x) = P2(x) + (1/3!)f'''(0)(x - 0)^3
= 0 + 16x + 8x^2 + (1/3!)(48sec^2(0)tan(0))(x - 0)^3
= 16x + 8x^2
Therefore, the Taylor polynomials of degree 2 and 3 centered at x = 0 for the function f(x) = 16tan(x) are:
P2(x) = 16x + 8x^2
P3(x) = 16x + 8x^2
Learn more about taylor polynomials at https://brainly.com/question/31978863
#SPJ11
Need Help! Please!
Tara found a pair of jeans that were regularly priced at $35. She has a coupon for 15% off. What is the price of the jeans after applying the coupon?
$20
$7
$29.75
$33.50
Answers
35-5.25=29.75
Answer:
The price is $29.75
Step-by-step explanation:
Because it is 15 percent off, that means that the jeans are priced at 100%-15%=85%. To convert a percent to a decimal, move the decimal two places to the left. This gives us .85. Multiply 35 by .85 and you will get 29.75. Hope this helps!
V = (pi r^2 h/3)...solve for h
Answers
Answer:
h = (3×V)/ (pi×r²)
Step-by-step explanation:
\(v = \frac{\pi {r}^{2} h}{3} \)
\(3 \times v = \pi {r}^{2} h\)
\(h = \frac{3v}{\pi {r}^{2} } \)
Suppose y varies inversely with x, and y = 49 when x = 17
. What is the value of x when y = 7 ?
Answers
Answer:
119 is the value of x when y = 7
Step-by-step explanation:
Since y varies inversely with x, we can use the following equation to model this:
y = k/x, where
k is the constant of proportionality.Step 1: Find k by plugging in values:
Before we can find the value of x when y = k, we'll first need to find k, the constant of proportionality. We can find k by plugging in 49 for y and 17 for x:
Plugging in the values in the inverse variation equation gives us:
49 = k/17
Solve for k by multiplying both sides by 17:
(49 = k / 17) * 17
833 = k
Thus, the constant of proportionality (k) is 833.
Step 2: Find x when y = k by plugging in 7 for y and 833 for k in the inverse variation equation:
Plugging in the values in the inverse variation gives us:
7 = 833/x
Multiplying both sides by x gives us:
(7 = 833/x) * x
7x = 833
Dividing both sides by 7 gives us:
(7x = 833) / 7
x = 119
Thus, 119 is the value of x when y = 7.
Brainliest question please help me answer this question please

Answers
Answer:
Step-by-step explanation:
The equation for a circle is
\((x-h)^2+(y-k)^2=r^2\)
We have our h and k from the center as h = -1 and k = -3, and we also know the radius, which is 6. We also have an x/y coordinate as (-6, -6) and we want to know if that coordinate lies in, on, or outside of the circle. The way we will do that is plug everything into the circle equation and solve. If what we solve for is less than the radius, then the point is inside the circle; if what we solve for is equal to the radius, then the point is on the circle; if what we solve for is greater than the radius, then the point in outside the circle. Here we go:
\((-6-(-1))^2+(-6-(-3))^2?36\) . There's a question mark there intentionally. The left side is the one we are solving for to see if it is less than, equal to, or greater than, 36. Continuing,
\((-6+1)^2+(-6+3)^2? 36\) and
\((-5)^2+(-3)^2?36\) and
25 + 9 ? 36
34 ? 36
We know that 34 is less than 36, so the point lies INSIDE the circle.
Answer:
a
Step-by-step explanation:
because it is in the circle
Solve 2x^2 - x ≥ -5. Show your work.
Answers
Answer:
\((x-\frac{1}{4})^{2} \geq \frac{-39}{16}\)
Step-by-step explanation:
Rewrite into standard form:
\(2x^{2} -x+5 \geq 0\)
Complete the square:
\(2(x-\frac{1}{4} )^{2} + \frac{39}{8} \geq 0\)
Subtract \(\frac{39}{8}\) from both sides:
\(2(x-\frac{1}{4})^{2} \geq \frac{-39}{8}\)
Divide both sides by 2:
\((x-\frac{1}{4})^{2} \geq \frac{-39}{\frac{8}{2}}\)
Simplify:
\((x-\frac{1}{4})^{2} \geq \frac{-39}{16}\)
. Describe how to get the mixed number answer to 19÷6 from the
whole-number-with-remainder
answer. By considering a simple word problem, explain why the
method you describe makes
sense."
Answers
To obtain the mixed number answer to 19 ÷ 6 from the whole-number-with-remainder answer, divide the numerator (19) by the denominator (6).
To find the mixed number answer to 19 ÷ 6, we divide 19 by 6. The whole-number quotient is obtained by dividing the numerator (19) by the denominator (6), which in this case is 3. This represents the whole number part of the mixed number answer, indicating how many complete groups of 6 are in 19. Next, we consider the remainder. The remainder is the difference between the dividend (19) and the product of the whole number quotient (3) and the divisor (6), which is 1. The remainder, 1, becomes the numerator of the fractional part of the mixed number.
This method makes sense because it aligns with the division process and provides a clear representation of the result. It shows the whole number part as the number of complete groups and the fractional part as the remaining portion. This representation is helpful in various real-world scenarios, such as dividing objects or quantities into equal groups or sharing items among a certain number of people.
Learn more about mixed number here:
https://brainly.com/question/24137171
#SPJ11
Two numbers each with two decimd
places round to 312 to one decima
place. The total of the numbers is
62.4, What could the numbers be?
You need to be clear on their understands
of rounding and what it means when f
Says two numbers each with two
decimal places, for example, they may
choose 3121+ 3419 both of which
round
to 31.2 when rounded to
I decimal place.
Fows on knowing that when rounding.
it is
Can they find all of these using
Systematic approach.
Answers
It is not possible to find two numbers with two decimal places that round to 312 when rounded to one decimal place and have a total of 62.4.
To solve this problem systematically, we can break it down into smaller steps:
Let's assume the two numbers are x and y, both with two decimal places.
We can represent them as x = a.b and y = c.d, where a, b, c, and d are digits.
Rounding x and y to one decimal place gives us the following equations:
Round(x) = a.b ≈ 312
Round(y) = c.d ≈ 312
Since the total of the numbers is 62.4, we have the equation:
x + y = a.b + c.d
= 62.4
From Step 2, we know that both a.b and c.d are approximately equal to 312.
So, we can write:
a.b ≈ 312
c.d ≈ 312
Since a.b and c.d are rounded to one decimal place, we can rewrite them as:
a.b = 312 + p
c.d = 312 + q
p and q are the decimal parts that were rounded.
Substituting the new representations of a.b and c.d into the equation from Step 3, we get:
(312 + p) + (312 + q) = 62.4
Simplifying the equation gives us:
624 + (p + q) = 62.4
Solving for (p + q), we have:
p + q = 62.4 - 624
= -561.6
Since p and q are decimal parts, they must be between 0 and 1. -561.6 is outside this range, which means there are no values for p and q that satisfy the given conditions.
For similar questions on decimal places
https://brainly.com/question/28393353
#SPJ8
For a point to be a solution to a
system of inequalities, the point
must make_ of the
inequalities true.
Answers
Answer:
The signs.Step-by-step explanation:
For a point to be a solution to a system of inequalities, the points must make the signs of the inequalities true.
For example, the points must give results like 2<3 or 0>-2, these are true solutions. If the points gives 1>2, then that point is not a solution.
Set both given equations equal to zero, then combine them into one standard form equation. Simplify if possible.
7x + 3 = 5 and y - 1 = 6
Equation 1 -
Equation 2 -
Combined Equation -
Answers:
a. 7x - 2 = 0
b. 7x - y = 1
c. 7x + 8 = 0
d. y - 7 = 0
e. 7x - y = -5
f. y + 7 = 0
Answers
The standard equation is 7x + y = 9
layoff Ax + By = C is the usual form for two-variable direct equations. A standard form direct equation is, for case, 2x + 3y = 5. When an equation is given in this format, chancing both intercepts is rather simple( x and y). When trying to break systems involving two direct equations, this form is also relatively helpful.
Given
7x + 3 = 5 and y - 1 = 6
Add the bottoms from the two given equations to produce a single standard-form equation.
By shifting the constant fromR.H.S. toL.H.S., the equations are reset to zero.
7x + 3 - 5 = 0
7x - 2 = 0----( 1)
y - 1 = 6
y - 1 - 6 = 0
y - 7 = 0-----( 2)
Equation 1 and equation 2 must be combined.
7x - 2 + y - 7 = 0
7x + y - 9 = 0
layoff Ax + By = C is the equation's conventional form.
A, B, and C are integers and x and y are variables in this type of equation.
Accordingly, the common equation is
7x + y - 9 = 0
7x + y = 9
therefore the standard equation is 7x + y = 9
To know more about Standard Equation, refer to this link:
https://brainly.com/question/16601835
#SPJ1
Leo is going to use a random number generator 400400400 times. Each time he uses it, he will get a 1, 2, 3,4,1,2,3,4,1, comma, 2, comma, 3, comma, 4, comma or 555.What is the best prediction for the number of times that Leo will get an odd number
Answers
The best prediction for the number of times that Leo will get an odd number is 200.
The probability of getting an odd number (1 or 3) is 2/4 = 1/2.
Using the expected value formula, we can predict the number of times that Leo will get an odd number:
Expected number of odd numbers = (probability of getting an odd number) x (total number of trials)
Expected number of odd numbers = (1/2) x (400) = 200
Therefore, the best prediction for the number of times that Leo will get an odd number is 200.
Learn more about probability
https://brainly.com/question/30034780
#SPJ4
an exponential function is expressed in the form y ab x the relation represents a growth when
Answers
Answer:
b > 1
Step-by-step explanation:
You want to know the conditions on an exponential function that represents growth.
Growth factorThe value of 'b' in the exponential function y = a·b^x is called the "growth factor." Each time x increases by 1 unit, the value of y is multiplied by 'b'. If that product is increasing, the value of 'b' must be greater than 1.
The relation represents growth when b > 1.
An exponential function in the form \(y = ab^x\) represents growth when the base (b) is greater than 1.
What is exponential function?In an exponential function of the form y = ab^x, the base (b) is a crucial component. The behavior of the function depends on the value of the base.
When the base (b) is greater than 1, it means that b is a positive number larger than 1. In this scenario, as the value of x increases, the value of \(b^x\) also increases exponentially. This results in the function \(y = ab^x\) exhibiting growth.
To better understand this growth behavior, let's consider an example. Suppose we have an exponential function \(y = 2^x\). As x increases from 0, the values of \(2^x\) will be as follows:
For x = 0, \(2^0\) = 1
For x = 1, \(2^1\) = 2
For x = 2, \(2^2\) = 4
For x = 3, \(2^3\) = 8
For x = 4, \(2^4\) = 16
As you can see, as x increases, the values of \(2^x\) grow exponentially. This demonstrates the growth behavior of exponential functions when the base is greater than 1.
It's important to note that when the base (b) is between 0 and 1 (exclusive), the exponential function will exhibit decay or decreasing behavior rather than growth.
In summary, an exponential function of the form \(y = ab^x\) represents growth when the base (b) is greater than 1. As x increases, the function values increase exponentially, indicating a growth pattern.
Learn more about exponential function on:
https://brainly.com/question/12626186
#SPJ4
name date period portfolio problem: squares and their friends find the area of the shaded square. explain your reasoning. the square below has sides of 2 cm. what is the radius of the circle?
Answers
The area of the shaded square is 4 square centimeters, and the radius of the circle is approximately 1.41 cm.
To find the area of the shaded square and the radius of the circle, we will follow these steps:
Step 1: Identify the dimensions of the square.
From the student question, we know that the square has sides of 2 cm each.
Step 2: Find the area of the square.
The area of a square can be calculated using the formula:
Area = side × side.
In this case, the area of the square is:
2 cm × 2 cm = 4 square centimeters.
Step 3: Find the diagonal of the square.
The diagonal of a square can be found using the Pythagorean theorem:
diagonal² = side² + side².
In this case, the diagonal² = 2 cm² + 2 cm² = 4 cm² + 4 cm² = 8 cm².
Taking the square root of both sides, we get: diagonal = √8 cm ≈ 2.83 cm.
Step 4: Find the radius of the circle.
Since the circle is inscribed in the square, its diameter is equal to the diagonal of the square.
Thus, the radius of the circle is half the diagonal.
Radius = diagonal ÷ 2 ≈ 2.83 cm ÷ 2 ≈ 1.41 cm.
For similar question on circle.
https://brainly.com/question/28162977
#SPJ11
Find the equation of the line shown.

Answers
to get the equation of any straight line, we simply need two points off of it, let's use those two in the picture below.
\((\stackrel{x_1}{-4}~,~\stackrel{y_1}{3})\qquad (\stackrel{x_2}{4}~,~\stackrel{y_2}{1}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{1}-\stackrel{y1}{3}}}{\underset{\textit{\large run}} {\underset{x_2}{4}-\underset{x_1}{(-4)}}} \implies \cfrac{-2}{4 +4} \implies \cfrac{ -2 }{ 8 } \implies - \cfrac{1}{4}\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{3}=\stackrel{m}{- \cfrac{1}{4}}(x-\stackrel{x_1}{(-4)}) \implies y -3 = - \cfrac{1}{4} ( x +4) \\\\\\ y-3=- \cfrac{1}{4}x-1\implies {\Large \begin{array}{llll} y=- \cfrac{1}{4}x+2 \end{array}}\)

Can someone help me!!
ASAP

Answers
Answer:
It would be 30
Step-by-step explanation:
6*5=30
what makes this bond correct
3/4+__=2
WHATS THE ANSWER
Answers
Answer:
The answer is 5/6.
Step-by-step explanation:
Lets start with a=1.
a+1=2, which is the denominator. (1/2)
Taking the same number as numerator, now, consider a=2.
a+1=3, denominator.(2/3)
Now, let a=3.
a+1==4, denominator for a=3. (3/4)
If continued a becomes equal to 4.
a+1=5, which is also the denominator. (4/5)
Now, since the denominator is 5, let a=5.
a+1=6, which will become the denominator. (5/6)
Thus the series follows a pattern of a/a+1.
Answer:
5/4
Step-by-step explanation:
Let's put the unknown value as X
To solve this equation, we must solve for x
First we need to isolate x, which means we need to get it by itself.
To do this, we must subtract 3/4 on both sides since it is being added.
This gets rid of 3/4 on the first side and changes the second side to whatever 2+3/4 is
This leaves us with x=5/4
Therefore, your answer is 5/4.
In the diagram below, lines h and s are parallel. If the m∠2 = 70°, what is the angle measurement of m∠7?
a. 70
b. 130
c. 7
d. 110

Answers
Answer:
c
Step-by-step explanation:
took it
Angles 2 and 7 are alternate exterior angles which are supplementary
180 - 70 = 110
I teach geometry
help please i don’t understand

Answers
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Triangles are similar ,
Thus :
\( \frac{9}{3} = \frac{6}{x} \\ \)
\(3 = \frac{6}{x} \\ \)
\( \frac{6}{x} = 3 \\ \)
Inverse both sides
\( \frac{x}{6} = \frac{1}{3} \\ \)
Multiply sides by 6
\(6 \times \frac{x}{6} = 6 \times \frac{1}{3} \\ \)
\(x = 2 \times 3 \times \frac{1}{3} \\ \)
\(x = 2\)
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
Two rays that share a common vertex?
Lines
Angles
Midpoint
Endpoint
Answers
Answer:
angles
Step-by-step explanation:
when two lines/rays intersect, they form angles
write 60 as the sum of two factors. in your expression write one of the factors as a sum of two numbers. Find an equivalent way to write this expression.
Answers
First number 30 and second number is 30 to write one of the factors as a sum of two numbers.
What do math factors mean?
A number or algebraic expression that evenly divides another number or expression—i.e., leaves no remainder—is referred to as a factor in mathematics. As an illustration, 3 and 6 are factors of 12 because 12 3 = 4 and 12 6 = 2, respectively. 1, 2, 4, and 12 are the other components that make up 12.any combination of numbers that results in a product when multiplied together. 1, 2, 3, and 6 are the factors of 6. factor. verb. factored; factoringLet first number 30 and second number is 30
then the sum of two factors
30+30=60
50+10=60
20×3=60
Learn more about factor
brainly.com/question/24182713
#SPJ1
Use two unit multipliers to convert 42 centimeters to feet.
Answers
Answer: 42 Centimeter
Step-by-step explanation: 42 Centimeter = 1.37795 Foot How to convert Centimeters to Feet 1 centimeter is equal to 0.0328083989 feet: 1cm = (1/2.54) inch = 0.0328083989ft the distance d in feet (ft) is equal to the distance d in centimeters (cm) divided by 30.48, that conversion formula
If U And V Are Orthogonal, What Is The Magnitude Of U Times V?
Answers
If U and V are orthogonal then the magnitude of U times V will be U.V = 0 or |UxV| = uv.
U and V are two orthogonal vectors.
since the angle between them is θ = 90⁰
let u and v be the magnitudes of the vectors U and V respectively.
so first dot-product: If two non-zero vectors are orthogonal than the dot product of these vectors will be zero. Dot product of two vectors is expressed by:
U.V = uv cosθ
since these vectors are orthogonal so,
U.V = uv cos90⁰ = 0
And Cross-product: Magnitude Cross product of two orthogonal vectors will be equal to product of magnitude of these vectors.
|UxV| = uv sin θ
|UxV| = uv sin 90⁰ = uv
Therefore, U.V = 0, |UxV| = uv.
To learn more about Cross-product:
https://brainly.com/question/29164170
#SPJ4
27 is 30% of what number?
A 8585
B 9292
C 1212
D 90
Answers
Answer:
27 is 30% of what number?
D. 90
Step-by-step explanation:
You're welcome.
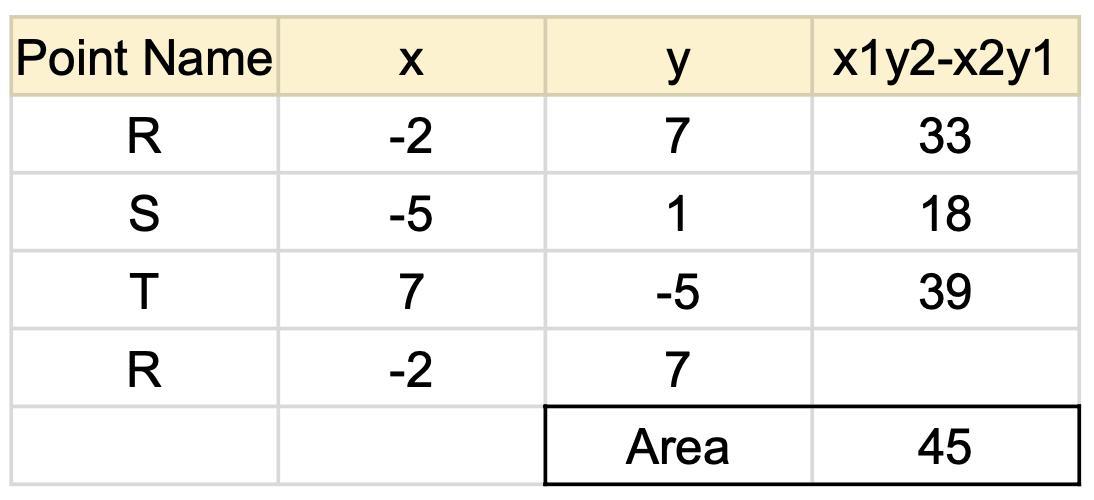
solve this
please i need help with this

Answers
Answer:
45
Step-by-step explanation:
You want the area of triangle RST using the area formula A=1/2bh, given the points R(-2, 7), S(-5, 1), and T(7, -5).
Side lengthsA plot of the points is shown in the first attachment. By counting grid squares, you can see that segment RS has a "rise" of 2 grid squares for each 1 to the right. The total (run, rise) is ...
R -S = (-2, 7) -(-5, 1) = (-2 +5, 7 -1) = (3, 6)
The length of RS is found using the Pythagorean theorem (distance formula). It is ...
RS = √(3² +6²) = √45 = 3√5
Similarly the length of segment ST is ...
T -S = (7, -5) -(-5, 1) = (7 +5, -5 -1) = (12, -6)
ST = √(12² +(-6)²) = √180 = 6√5
SlopesWe note that the slopes of these segments are opposite inverses of each other:
slope RS = 6/3 = 2
slope ST = -6/12 = -1/2
This means the segments are at right angles. One of them can be considered to be the "base" and the other the "height" of the triangle.
AreaUsing the area formula, we find the area to be ...
A = 1/2bh
A = 1/2(6√5)(3√5) = (1/2·6·3)(√(5·5)) = 9·5 = 45
The area of ∆RST is 45 square units.
__
Alternate solution
When the coordinates of a polygon are given, there are several other ways to find its area. One of these is illustrated in the second attachment.
The method illustrated here computes successive "determinants", then finds the area as half the absolute value of their sum. (The sign of the sum will depend on the order in which the points are listed around the figure. Here, it is counterclockwise.) As you can see, we get the same result. You can also see that a spreadsheet is useful for doing the repetitive math.
Area ∆RST = 45 square units
__
Additional comment
The distance formula for the length of the segment between two points is ...
d = √((x2-x1)² +(y2-y1)²)
Above, we calculated the differences (x2-x1, y2-y1) separately, then used the "root sum squares" formula for the distance. This has the advantage that (y2-y1)/(x2-x1) is the slope of the segment, and we needed to make sure the segments were perpendicular.