Question
A town's yearly snowfall in inches over a 10-year period is recorded in this table.
What is the mean of the snowfall amounts?
Responses
15.0 in.
15.0 in.
17.0 in.
17.0 in.
17.9 in.
17.9 in.
Year Snowfall in inches
1997 15
1998 11
1999 18
2000 25
2001 13
2002 20
2003 16
2004 28
2005 15
2006 18
18.9 in
18.9 in
Answers
The mean (average) of the snowfall amounts is 17.9 inches.
What is mean?In statistics, the mean is a measure of central tendency that represents the average value of a dataset. It is calculated by summing up all the values in the dataset and then dividing the result by the total number of values.
What is average?In statistics, the terms "mean" and "average" are often used interchangeably to refer to the same concept. Both terms represent a measure of central tendency that represents the typical or average value of a dataset.
According to given information:To find the mean (average) of the snowfall amounts, we need to add up all the snowfall amounts and divide by the total number of years.
Adding up the snowfall amounts:
15 + 11 + 18 + 25 + 13 + 20 + 16 + 28 + 15 + 18 = 179
Dividing by the total number of years (10):
179/10 = 17.9
So the mean (average) of the snowfall amounts is 17.9 inches.
Therefore, the correct response to the mean is 17.9 in.
To know more about mean visit:
https://brainly.com/question/1136789
#SPJ1
Related Questions
Write an equation of a line that passes through the point (3,0) and is perpendicular to the line y=−1/2x−4.
Answers
Answer:
Step-by-step explanation:
perp. 2
y - 0 = 2(x - 3)
y = 2x - 6
In Problems 1 through 14, the values of a periodic function f(t) in one full period are given; at each discontinuity the value of f(t) is that given by the average value condition in (13). Sketch the graph of f and find its Fourier series. It 11. f(t) = cos -1
Answers
The graph of f(t) = cos^-1(t) will be a periodic function with a range limited to the interval [-1, 1]. Since the function is defined for the entire period, there are no discontinuities in this case. The graph of f(t) will resemble a curve that oscillates between -1 and 1, centered around the y-axis. The Fourier series for f(t) can be found by calculating the coefficients of the harmonics.
1. The function f(t) = cos^-1(t) has a limited range of [-1, 1] and is defined for the entire period.
2. Since there are no discontinuities, we don't need to apply the average value condition mentioned in (13).
3. To find the Fourier series of f(t), we need to calculate the coefficients for each harmonic term.
4. The general form of a Fourier series for a periodic function f(t) is given by:
f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt)), where ω is the angular frequency.
5. Since f(t) is an even function, the bn coefficients will be zero.
6. The constant term a0 can be found by taking the average of f(t) over one period, which is (2/π) multiplied by the integral of f(t) from -π to π.
7. The coefficients an can be calculated using the formula: an = (2/π) * integral of f(t)*cos(nωt) from -π to π.
8. Substitute the expression for f(t) = cos^-1(t) into the formula for an and integrate to find the values of an for each harmonic term.
9. The Fourier series of f(t) will then be the sum of the constant term a0 and the series of the an*cos(nωt) terms.
10. Sketch the graph of f(t) using the calculated Fourier series coefficients to visualize the function.
Learn more about frequency : brainly.com/question/29739263
#SPJ11
Which one of the following is odd man out
a. 9 b. 81 c. 315 d. 661
Answers
Here, we are given 4 numbers as 9, 81, 315 and 661 and we have to pick the odd man out, i.e., the number which is different from the other three in a particular way. So, analyzing the pattern followed in the numbers, we can say that the correct answer i.e., the number which is different from the rest is \(661\).
The term 'odd man out' is used to refer to an item or entity in a group that is different from the others. This term is commonly used in puzzles and quizzes where a group of items or numbers are given, and one of them is to be identified as the odd one out. To arrive at the answer, one needs to look for a pattern or a commonality between the numbers.
This concept of identifying the odd one out is commonly used in cognitive tests, as it requires logical and analytical thinking. It also helps in developing problem-solving skills and critical thinking abilities, which are essential in many fields of work and study.
In this case, it is observed that \(9\), \(81\), and \(315\) are all multiples of \(9\) i..e, perfectly divisible by \(9\) as follows,
\(\frac{9}{9}=1\)
\(\frac{81}{9}=9\)
\(\frac{315}{9}=35\)
But, if we divide \(661\) by \(9\), it won't be perfectly diviisble. So, \(661\) does not belong to the given group of numbers. Hence it is the odd man out in the given group.
Learn more about multiples here:
https://brainly.com/question/96515
#SPJ11
about 42% of a population are of a particular ethnic group. 180 people are randomly selected from this population. round all answers to 3 decimal places. convert the percentage of the population to a decimal: p: .42 correct compute the mean and standard of this size sample of this binomial distribution: mean: 75.6 correct standard deviation: 6.622 correct
Answers
The percentage of the population in decimal is p=0.42
The mean of the sample of the binomial distribution=75.6
The standard deviation of the sample of the binomial distribution=6.622
How to convert a decimal to a percentage?
To convert a decimal number into a percentage value, multiply the decimal by 100.
What is binomial distribution?
The binomial distribution gives out either success or failure as two possible results in an experiment, is the discrete probability distribution used in probability theory and statistics.
Given that,
p = 42% = 0.42
q = 1 - p = 1 - 0.42 = 0.58
n = 180
Using the binomial distribution,
mean = \(n \times p\) = \(180 \times 0.42\) = 75.6
standard deviation = \(\sqrt{n \times p \times q}\) = \(\sqrt{180 \times 0.42 \times 0.58}\) = 6.622
To learn more about the binomial distribution from the given link
https://brainly.com/question/15246027
#SPJ4
The percentage of the population in decimal is p=0.42
The mean of the sample of the binomial distribution=75.6
The standard deviation of the sample of the binomial distribution=6.622
How to convert a decimal to a percentage?
To convert a decimal number into a percentage value, multiply the decimal by 100.
What is binomial distribution?
The binomial distribution gives out either success or failure as two possible results in an experiment, is the discrete probability distribution used in probability theory and statistics.
Given that,
p = 42% = 0.42
q = 1 - p = 1 - 0.42 = 0.58
n = 180
Using the binomial distribution,
mean = 75.6
standard deviation = 6.622
To learn more about the binomial distribution from the given link
https://brainly.com/question/9325204
#SPJ4
At the beginning of the school year, Oak Hill Middle School has 480 students. There are 270 seventh graders and 210 eighth graders
Answers
At the beginning of the school year, Oak Hill Middle School has a total of 480 students. Out of these students, there are 270 seventh graders and 210 eighth graders.
To determine the total number of students in the school, we add the number of seventh graders and eighth graders:
270 seventh graders + 210 eighth graders = 480 students
So, the number of students matches the total given at the beginning, which is 480.
Additionally, we can verify the accuracy of the information by adding the number of seventh graders and eighth graders separately:
270 seventh graders + 210 eighth graders = 480 students
This confirms that the total number of students at Oak Hill Middle School is indeed 480.
Therefore, at the beginning of the school year, Oak Hill Middle School has 270 seventh graders, 210 eighth graders, and a total of 480 students.
Learn more about graders here
https://brainly.com/question/33002456
#SPJ11
Consider the following. (Round your answers to three decimal places.)
x2/4+ y2/1 = 1
(a) Find the area of the region bounded by the ellipse.
(b) Find the volume and surface area of the solid generated by revolving the region about its major axis (prolate spheroid).
(c) Find the volume and surface area of the solid generated by revolving the region about its minor axis (oblate spheroid). volume surface area
Answers
(a) The area of the region bounded by the ellipse is π. (b) When the region is revolved about its major axis, it generates a prolate spheroid with volume of 4π and surface area of 8π. (c) When the region is revolved about its minor axis, it generates an oblate spheroid with volume of 4π and surface area of 6π.
(a) The equation of the ellipse is x^2/4 + y^2/1 = 1, which represents an ellipse centered at the origin with semi-major axis 2 and semi-minor axis 1. The area of an ellipse is given by A = πab, where a and b are the lengths of the semi-major and semi-minor axes, respectively. In this case, A = π(2)(1) = π.
(b) When the region bounded by the ellipse is revolved about its major axis, it generates a prolate spheroid. The volume of a prolate spheroid is given by V = (4/3)πa^2b, and the surface area is given by A = 4πa^2, where a is the semi-major axis and b is the semi-minor axis. Substituting the values, we get V = (4/3)π(2^2)(1) = 4π and A = 4π(2^2) = 8π.
(c) When the region bounded by the ellipse is revolved about its minor axis, it generates an oblate spheroid. The volume of an oblate spheroid is given by V = (4/3)πa^2b, and the surface area is given by A = 2πa(b + a), where a is the semi-major axis and b is the semi-minor axis. Substituting the values, we get V = (4/3)π(2^2)(1) = 4π and A = 2π(2)(1 + 2) = 6π.
Learn more about oblate spheroid here:
https://brainly.com/question/28184317
#SPJ11
Work out the surface area of this cylinder.
Height=25
Diameter=12

Answers
x/4 +6 ≤ x+8 inequality
Answers
Answer:
Solution in photo
Step-by-step explanation:

Please help I’ll give brainliest!!

Answers
Answer:
hey, good afternoon
Step-by-step explanation:
-4x^2+16x+84 you put the -4x^2+16x in parenthesis. so it looks like this
(-4x^2+16x)+84
-4(x^2 - 4x -21)
-4(x^2+3x-7x-21 the bold numbers are the common factors.
the solution to this problem is
-4(x-7)(x+3)
i think this is right hope this helps
Answer:
x= +- 2+\(\sqrt{3}\) /4
Step-by-step explanation:
(T/F) a shadow price indicates how much the optimal value of the objective function will increase per unit increase in the right-hand side of a constraint.
Answers
The statement " a shadow price indicates how much the optimal value of the objective function will increase per unit increase in the right-hand side of a constraint" is true because shadow prices provide valuable information about the marginal value of resources and constraints in linear programming problems
A shadow price represents the marginal value of a resource or constraint in a linear programming problem. It indicates how much the optimal value of the objective function will increase if the right-hand side of a constraint is increased by one unit, while keeping all other constraints and variables fixed. The shadow price of a constraint is calculated by adding one unit to the right-hand side of the constraint and re-solving the linear programming problem.
The resulting increase in the objective function value is the shadow price of that constraint. Shadow prices are useful in making decisions about resource allocation, pricing, and capacity planning in a variety of industries such as manufacturing, transportation, and energy.
Learn more about shadow price here
brainly.com/question/30755524
#SPJ4
help please lol :)).

Answers
Answer:
$10.50
Step-by-step explanation:
Jamie ran the first 2000 meters in 6 minutes. At that rate, how long would it take Jaime to run 5000 meters?
Answers
Answer:
15 minutes
Step-by-step explanation:
To figure this out, you can create a ratio. If we say the first 2000 miles is the 1 in the ratio, the ratio would be 1 : 2.5. Since it took 6 minutes for the first 2000, you have to multiply 6 by 2.5 to get your answer of 15 minutes.
List the sample space for rolling a fair eight-sided die.
S = {1}
S = {8}
S = {1, 2, 3, 4, 5, 6}
S = {1, 2, 3, 4, 5, 6, 7, 8}
Answers
The sample space for rolling a fair eight-sided die is {1, 2, 3, 4, 5, 6, 7, 8}.
We have to find the sample space for rolling a fair eight-sided die.
The sample space for rolling a fair eight-sided die consists of all the possible outcomes of a single roll of the die.
As the die has eight sides numbered from 1 to 8, the sample space can be represented as:
S = {1, 2, 3, 4, 5, 6, 7, 8}
Therefore, the sample space for rolling a fair eight-sided die is {1, 2, 3, 4, 5, 6, 7, 8}.
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ1
After two consecutive years of 6% losses, what rate of return in the third year will produce a cumulative gain of 7%? Note: Please make sure your final answer(s) are in percentage form and are accurate to 2 decimal places. For example 34.56%. Rate of return = 0.00 %
Answers
The rate of return of approximately 17.95% in the third year would produce a cumulative gain of 7% after two consecutive years of 6% losses.
To solve the problem completely, let's calculate the rate of return required in the third year to achieve a cumulative gain of 7% after two consecutive years of 6% losses.
1. Calculate the total loss over the two years:
Total loss = (1 - 0.06) * (1 - 0.06) = 0.9416
2. Calculate the target cumulative gain:
Cumulative gain = 1 + 0.07 = 1.07
3. Set up the equation to solve for the rate of return:
1 + Rate of return = Cumulative gain / (1 - Total loss)
4. Substitute the values into the equation:
1 + Rate of return = 1.07 / (1 - 0.9416)
1 + Rate of return = 1.07 / 0.0584
5. Solve for the rate of return:
Rate of return = (1.07 / 0.0584) - 1
Rate of return ≈ 17.95%
Therefore, a rate of return of approximately 17.95% in the third year would be needed to achieve a cumulative gain of 7% after two consecutive years of 6% losses.
To know more about calculating the rate of return, refer here:
https://brainly.com/question/17164328#
#SPJ11
Find an equation of the line that satisfies the given conditions.
Passes through (3,7); parallel to the line passing through (4,5) and (0,1)
.
Answers
The equation of the line that passes through (3,7) and is parallel to the line passing through (4,5) and (0,1) is y = x + 4.
To find an equation of the line that passes through the point (3,7) and is parallel to the line passing through (4,5) and (0,1), we first need to determine the slope of the line passing through (4,5) and (0,1), which is the same as the slope of the parallel line we are trying to find.
The slope of a line passing through two points (x₁, y₁) and (x₂, y₂) can be found using the slope formula:
m = (y₂ - y₁) / (x₂ - x₁)
Applying this formula to the points (4,5) and (0,1), we get:
m = (1 - 5) / (0 - 4) = -4 / -4 = 1
Therefore, the slope of the line we are trying to find is 1.
Using the point-slope form of the equation of a line, we can write the equation of the line passing through (3,7) with a slope of 1 as:
y - 7 = 1(x - 3)
Simplifying the equation, we get:
y = x + 4
To learn more about equation click on,
https://brainly.com/question/28634146
#SPJ4
which of the following represents the factorization of the binomial below 49x^2-81y^2
Answers
Answer:
(7x + 9y) (7x - 9y)
Step-by-step explanation:
Factorization of binomial:49x² - 81y² = 7²*x² - 9²*y²
= (7x)² - (9y)²
\(\boxed{\text{\bf Use the identity $ a^2 - b^2 = (a + b)(a-b)$} }\)
Here, 'a' corresponds to 7x and 'b' corresponds to 9y.
= (7x + 9y) (7x -9y)
Consider the problem: Mai has $36 to spend on movie tickets. Each movie ticket costs $4.50. How many tickets can she buy? Part 1: Select BOTH a multiplication equation AND a division equation to represent this situation. Group of answer choices 4.50 ÷ 36 = ? ? · 4.50 = 36 4.50 · 36 = ? 36 ÷ 4.50 = ?
Answers
Answer:
Multiplication:
4.5x = 36 or ? · 4.50 = 36
Division:
Total cost / cost per ticket = number of tickets or 36 ÷ 4.50 = ?
ill give brainliest :)))))))

Answers
\(m\angle S=\sin\dfrac{\sqrt{111}}{2\sqrt{37}}=\sin\dfrac{\sqrt3}{2}=60^{\circ}\)
Answer:
Step-by-step explanation:
sin S = UT/US
sin S = root(111) / 2root(37)
sin S = root(3).root(37) / 2root(37)
sin S = root(3)/2
S = 60
2. How are the integers and rational numbers different?
Answers
Answer:
Here --->
Step-by-step explanation:
Integers are "whole numbers" which is negative numbers, positive numbers, and 0. rational numbers are fractions, decimals, negative numbers, positive numbers, and 0. Hope this helps! :]]
A certain state uses the progressive tax rate below for
calculating individual income tax. Calculate the state
income tax owed on an $80,000 per year salary.
Hint: Subtract the income range from the total yearly
salary as you move through each bracket. This will help
you to calculate the income amount for the last bracket..
Income
Progressive
Range ($)
Tax Rate
0 - 3000
2%
3,000 • 0.02 = 60
3001 - 5000
3%
2,000 • 0.03 = 60
5001 - 17,000
5%
12,000 • 0.05 = 600
17,001 and up
5.75%
63,000 • 0.0575 = [?]

Answers
Answer: $4,222.50.
Step-by-step explanation:
given data 4,y,9,5,2,7 find y if the mode is 4
the mean is 5
the median is 6
Answers
Answer:
y = 3
Step-by-step explanation:
y , 2 , 4 , 5 , 7, 9
Mean = 5
\(\frac{4+y+9+5+2+7}{6}=5\\\\\frac{y+27}{6}=5\\\\y+27 = 5*6\\y +27=30\\y=30-27\\y = 3\)
What is 4 divided by 1/4
Answers

sixteen because if u but a 1 under neath the 4 then cross up and multiply 4×4 is 16 then1×1 is 1 so ur answer would be 16
2 2.1 Mathematical intro show that there is another form for spherical harmonics: 1 3 3 Y₁ x iy 1/√√2 (²-1) 2πT 2π 1 3 3 z YO 2 2π π r 1 3 x iy Y₁¹ 3 2π - - 12 √ √ 2² (²+²) 2 2π
Answers
Spherical harmonics are an integral part of quantum mechanics. They describe the shape of the orbitals, which electrons occupy in atoms. Moreover, the spherical harmonics provide the angular distribution of a wave in spherical coordinates. In 3D, the spherical harmonics can be written as:
Ylm(θ, φ) = √(2l + 1)/(4π) * √[(l - m)!/(l + m)!] * Plm(cosθ) * e^(imφ)
Here, l and m are known as the angular quantum numbers. They define the shape and orientation of the orbital. Plm(cosθ) represents the associated Legendre polynomial, and e^(imφ) is the exponential function. The spherical harmonics have various forms, including:
Y1,1 = -Y1,-1 = 1/2 √(3/2π) sinθe^(iφ)
Y1,0 = 1/2 √(3/π)cosθ
Y2,2 = 1/4 √(15/2π)sin²θe^(2iφ)
Y2,1 = -Y2,-1 = 1/2 √(15/2π)sinθcosφ
Y2,0 = 1/4 √(5/π)(3cos²θ-1)
Y0,0 = 1/√(4π)
The spherical harmonics have various applications in physics, including quantum mechanics, electrodynamics, and acoustics. They play a crucial role in understanding the symmetry of various systems. Hence, the spherical harmonics are an essential mathematical tool in modern physics. Thus, this is how one can show another form for spherical harmonics.
To know more about Spherical harmonics visit
https://brainly.com/question/23067012
#SPJ11
WILL MARK BRAINLIEST!!! Please solve the whole page with work!! It will be very much appreciated and I will heart the correct comment and give it 5 stars

Answers
Answer:
its only 5 points tho :c
Step-by-step explanation:
NEED HELP ASAP
Nyla invested $200 in an account with a 0.75% annual interest rate.
She made no deposits or withdrawals on the account for 3 years. If
interest was compounded annually, what is the balance in her bank
account at the end of 3 years?
Answers
Answer:
$50
Step-by-step explanation:
$200-0.75%=50
0.75%=150
Which transformation was performed on PQRS to form P'QʻR'S'? (1 point)
1) A dilation factor of 2
2) A dilation factor of 4
3) A dilation factor of 1/2
4) A dilation factor of 1/4

Answers
Given:
A transformation was performed on PQRS to form P'QʻR'S'.
To find:
The transformation.
Solution:
The given graph shows two similar polygons. It means, dilation was performed.
From the given graph it is clear that,
\(PS=2\) units
\(P'S'=1\) units
Now,
\(\text{Scale factor}=\dfrac{P'S'}{PS}\)
\(\text{Scale factor}=\dfrac{1}{2}\)
A dilation factor of \(\dfrac{1}{2}\) was performed on PQRS to form P'QʻR'S'.
Therefore, the correct option is (3).
assuming a constant growth factor, by what percent did the population of gotham city grow each year? give at least 3 decimal places.
Answers
Assuming a constant growth factor, the population of Gotham City grew by approximately 4.287% each year.
This can be calculated using the formula for exponential growth, which is:
y = a * (1 + r)^t
Where: y = final value of the population
a = initial value of the population
r = annual growth rate expressed as a decimal
t = number of years
For this problem, let's assume that the initial population of Gotham City was 100,000 and that the population grew for 10 years.
Using these values, we can calculate the annual growth rate as follows:
100,000 * (1 + r)^10 = final population
r = (final population / 100,000)^(1/10) - 1
Plugging in a final population of 148,644 (which is a 48.644% increase from the initial population),
r = (148,644 / 100,000)^(1/10) - 1r = 0.04287 (rounded to 5 decimal places)
Therefore, the annual growth rate (or percentage increase) is approximately 4.287% (rounded to 3 decimal places).
To know more about growth rate refer here:
https://brainly.com/question/13870574
#SPJ11
For what value of x must the quadrilateral be a parallelogram?
X=
(3x+28
work:

Answers
The value of x in the parallelogram is 9.3.
How to find the angle of a parallelogram?A parallelogram is a quadrilateral that has opposite sides equal to each other. Opposite sides of a parallelogram is also parallel to each other.
The opposite angle of a parallelogram are congruent while consecutive angles of a parallelogram are supplementary.
Therefore,
5x = 2x + 28
5x - 2x = 28
3x = 28
divide both sides of the equation by 3
x = 28 / 3
x = 9.333333
Therefore,
x = 9.3
learn more on parallelogram here: https://brainly.com/question/24022178
#SPJ1
Solve this system of equations, then determine what x equals.
x + 5y= 7
2x + 4y = -4
X=-18 x=3
X=-8
X=7
Answers
Answer:
−18=7
y=4/5
y=−5/2
y=4/5
X=−18
x=3
−18=−8
A piece of pizza with a diameter of 20 inches is eaten and m∠IPZ=45°. What is the perimeter of the piece of the pizza eaten in inches?
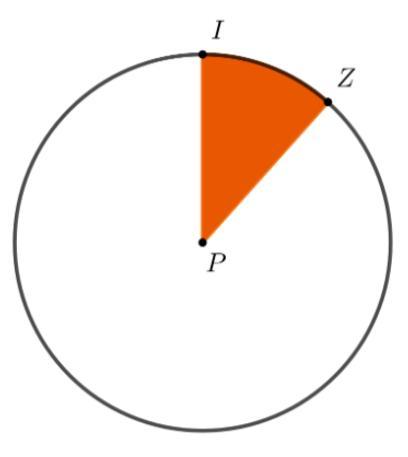
Answers
Answer:
Perimeter of pizza slice = 27.85 inches (Approx.)
Step-by-step explanation:
Given:
Diameter of pizza = 20 inches
So,
Radius of pizza slice = Diameter of pizza / 2
Radius of pizza slice = 20 / 2 = 10 inches
∠IPZ = 45°
Find:
Perimeter of pizza slice
Computation:
Perimeter of pizza slice = 2[Radius of pizza slice] + [θ/360][2πr]
Perimeter of pizza slice = 2[10] + [45/360][(2)(22/7)(10)]
Perimeter of pizza slice = 20 + [0.125][(2)(3.14)(10)]
Perimeter of pizza slice = 20 + [0.125][62.8]
Perimeter of pizza slice = 20 + 7.85
Perimeter of pizza slice = 27.85 inches (Approx.)
The perimeter of the slice of the pizza that is eaten, measured in inches, for the considered case, is 31.9635 inches.
How to find the relation between angle subtended by the arc, the radius and the arc length?\(2\pi^c = 360^\circ = \text{Full circumference}\)
The superscript 'c' shows angle measured is in radians.
If radius of the circle is of r units, then:
\(1^c \: \rm covers \: \dfrac{circumference}{2\pi} = \dfrac{2\pi r}{2\pi} = r\\\\or\\\\\theta^c \: covers \:\:\: r \times \theta \: \rm \text{units of arc}\)
For this case, we're given that:
Angle m∠IPZ=45°.Diameter of the circular pizza = 20 inchesNot using the above formula, but the concept, we know that:
360° covers full arc, which is \(2\pi r\) inch lengthed long.45° is 360°/8, so it will cover \(2\pi r/8\) inch long arc (the arc IZ).Since diameter of pizza = 20 inches, its radius r = 10 inches.
Thus, the length of the arc IZ = \(\dfrac{2 \times \pi \times 10}{8} \approx 1.9635 \: \rm inches.\)
Perimeter of the slice of the pizza eaten = sum of the length of its boundaries = Length of arc IZ + length of line IP + length of line ZP
Since line IP and ZP are radius, thus:
Perimeter of the slice of the pizza eaten ≈ 1.9635 + 10 + 10 = 31.9635 inches.
Thus, the perimeter of the slice of the pizza that is eaten, measured in inches, for the considered case, is 31.9635 inches.
Learn more about angle, arc length relation here:
https://brainly.com/question/15451496