Answers
Related Questions
Evaluate each of the following complex numbers and express the result in rectangular form:
a. z1= 3ejπ/4
b. z3= 2e-jπ/2
c. z4=j3
d. z5= j-4
Answers
Answer:
a. \(z_{1} = \frac{3\sqrt{2}}{2}+j\cdot 3\frac{\sqrt{2}}{2}\), b. \(z_{3} = -j\cdot 2\), c. \(z_{4} = -j\), d. \(z_{5} = 1\)
Step-by-step explanation:
All given complex numbers are in polar form, which are characterized by:
\(z = r\cdot e^{j\cdot \theta}\)
Where:
\(r\) - Magnitude, dimensionless.
\(\theta\) - Direction, measured in radians.
The rectangular form of complex numbers is represented by:
\(z = r\cdot (\cos \theta + j\cdot \sin \theta)\)
Now, each complex number is evaluated:
a. \(z_{1} = 3\cdot e^{j\cdot \frac{ \pi}{4} }\)
\(r = 3\) and \(\theta = \frac{\pi}{4}\)
\(z_{1} = 3\cdot \left(\cos \frac{\pi}{4}+j\cdot \sin \frac{\pi}{4} \right)\)
\(z_{1} = \frac{3\sqrt{2}}{2}+j\cdot 3\frac{\sqrt{2}}{2}\)
b. \(z_{3} = 2\cdot e^{-j\cdot \frac{\pi}{2} }\)
\(r = 2\) and \(\theta = -\frac{\pi}{2}\)
\(z_{3} = 2\cdot \left[\cos \left(-\frac{\pi}{2}\right) + j\cdot \sin \left(-\frac{\pi}{2} \right) \right]\)
\(z_{3} = -j\cdot 2\)
c. \(z_{4} = j^{3}\)
By definition of complex number, \(j = \sqrt{-1}\), which means that \(j^{2} = -1\). Hence:
\(z_{4} = j^{2+1}\)
\(z_{4} = j^{2}\cdot j\)
\(z_{4} = j\cdot j^{2}\)
\(z_{4} = -j\)
d. \(z_{5} = j^{-4}\)
By definition of complex number, \(j = \sqrt{-1}\), which means that \(j^{2} = -1\).
Hence:
\(z_{5} = \frac{1}{j^{4}}\)
\(z_{5} = \frac{1}{j^{2+2}}\)
\(z_{5} = \frac{1}{j^{2}\cdot j^{2}}\)
\(z_{5} = \frac{1}{(-1)\cdot (-1)}\)
\(z_{5} = 1\)
Diego scored nine points less than Andre in the basketball team Noah scored twice as many points as Diego if Noah scored 10 points how many ponts did Andre score
Answers
Answer:
1..........................
Answer:
Andre scored 14 points.
Step-by-step explanation:
set up expressions with the info given:
Diego's points: a –9
Andre's points: 2d. and
n = 2d
Noah's points = 10
Use the expressions to set up equations to solve.
To find a, Andre's points, we can work backwards.
Substitute the 10 from the last expression for n in the equation n=2d, and solve for d:
10 = 2d. Divide both sides by 2
5 = d
Substitute the value of d, Diego's points, to make an equation using the first expression:
5 = a –9 Add 9 to both sides.
5 + 9 = a a = 14
Andre scored 14 points
20 POINTS TO WHOEVER ANSWERS

Answers
Given that p(x)=2(5−x)2+1 , what is the value of p(-4)? Responses
Answers
Answer:
37
Step-by-step explanation:
x=-4
=2(5-(-4)2+1
=2(5+4)2+1
=2(9)2+1
=18(2)+1
=36+1
=37
Given that 8 tan = 3 cos
a) Show that the above equation can be rewritten in the form 3 sin2 + 8 sin − 3 = 0
b) Hence solve, for 0 ≤ ≤ 90, the equation 8 tan 2 = 3 cos 2, giving your answers to 2 decimal places.
Answers
The only solution for the equation 8 tan^2 θ = 3 cos^2 θ in the given Range is θ ≈ 19.47 degrees.
a) We are given the equation 8 tan θ = 3 cos θ.
Dividing both sides of the equation by cos θ, we have:
8 tan θ / cos θ = 3
Using the identity tan θ = sin θ / cos θ, we can substitute it into the equation:
8 (sin θ / cos θ) / cos θ = 3
Simplifying further, we get:
8 sin θ / cos^2 θ = 3
Now, multiplying both sides of the equation by cos^2 θ, we have:
8 sin θ = 3 cos^2 θ
Using the identity cos^2 θ = 1 - sin^2 θ, we can substitute it into the equation:
8 sin θ = 3(1 - sin^2 θ)
Expanding the equation, we get:
8 sin θ = 3 - 3 sin^2 θ
Rearranging the terms, we have:
3 sin^2 θ + 8 sin θ - 3 = 0
Therefore, we have successfully shown that the equation can be rewritten in the form 3 sin^2 θ + 8 sin θ - 3 = 0.
b) Now, let's solve the equation 3 sin^2 θ + 8 sin θ - 3 = 0.
To solve the quadratic equation, we can use factoring, quadratic formula, or other appropriate methods.
In this case, the equation factors as:
(3 sin θ - 1)(sin θ + 3) = 0
Setting each factor equal to zero, we have two equations:
3 sin θ - 1 = 0 or sin θ + 3 = 0
For the first equation, solving for sin θ, we get:
3 sin θ = 1
sin θ = 1/3
Taking the inverse sine (sin^-1) of both sides, we find:
θ = sin^-1(1/3) ≈ 19.47 degrees (to 2 decimal places)
For the second equation, solving for sin θ, we have:
sin θ = -3
Since the range of sine is between -1 and 1, there are no solutions for this equation in the given range (0 ≤ θ ≤ 90 degrees).
Therefore, the only solution for the equation 8 tan^2 θ = 3 cos^2 θ in the given range is θ ≈ 19.47 degrees.
To know more about Range .
https://brainly.com/question/30389189
#SPJ11
Add the two expressions.
−4.2x+3 and 2.5x−6
Answers
Combine like terms
Simplified:
-1.7x-3 is your answer
4.009 x 10-3 in decimal form
Answers
Answer:
the 3 represent a one thousand
so that means 4.oo9* 1000 = =49
100 POINTS
A gazebo in the shape of a regular octagon has equal sides of 9 feet and an apothem of 10.9 feet.
a. If one side of a gazebo is open, and the other sides have a railing, find the cost of the railing if it sells for $7.90 per foot.
b. Find the area of the gazebo in square feet.
c. Find the cost of the gazebo's flooring if it costs $3 per square foot. Round to the nearest hundred dollars.
Answers
Answer:
a) $497.70
b) 392.4 square feet
c) $1,200
Step-by-step explanation:
Part (a)A regular octagon has 8 sides of equal length.
Given each side of the octagon measures 9 feet in length, and one side does not have a railing, the total length of the railing is 7 times the length of one side:
\(\textsf{Total length of railing}=\sf 7 \times 9\; ft=63\;ft\)
If the railing sells for $7.90 per foot, the total cost of the railing can be calculated by multiplying the total length by the cost per foot:
\(\textsf{Total cost of railing}=\sf 63\;ft \times \dfrac{\$7.90}{ft}=\$497.70\)
Therefore, the cost of the railing is $497.70.
\(\hrulefill\)
Part (b)To find the area of the regular octagonal gazebo, given the side length and apothem, we can use the area of a regular polygon formula:
\(\boxed{\begin{minipage}{6cm}\underline{Area of a regular polygon}\\\\$A=\dfrac{n\;s\;a}{2}$\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the length of one side.\\ \phantom{ww}$\bullet$ $a$ is the apothem.\\\end{minipage}}\)
Substitute n = 8, s = 9, and a = 10.9 into the formula and solve for A:
\(\begin{aligned}\textsf{Area of the gazebo}&=\sf \dfrac{8 \times 9\:ft \times10.9\:ft}{2}\\\\&=\sf \dfrac{784.8\;ft^2}{2}\\\\&=\sf 392.4\; \sf ft^2\end{aligned}\)
Therefore, the area of the gazebo is 392.4 square feet.
\(\hrulefill\)
Part (c)To calculate the cost of the gazebo's flooring if it costs $3 square foot, multiply the area of the gazebo found in part (b) by the cost per square foot:
\(\begin{aligned}\textsf{Total cost of flooring}&=\sf 392.4\; ft^2 \times \dfrac{\$3}{ft^2}\\&=\sf \$1177.2\\&=\sf \$1200\; (nearest\;hundred\;dollars)\end{aligned}\)
Therefore, the cost of the gazebo's flooring to the nearest hundred dollars is $1,200.
a. To find the perimeter of the gazebo, we can use the formula P = 8s, where s is the length of one side. Substituting s = 9, we get:
P = 8s = 8(9) = 72 feet
Since one side is open, we only need to find the cost of railing for 7 sides. Multiplying the perimeter by 7, we get:
Cost = 7P($7.90/foot) = 7(72 feet)($7.90/foot) = $4,939.20
Therefore, the cost of the railing is $4,939.20.
b. To find the area of the gazebo, we can use the formula A = (1/2)ap, where a is the apothem and p is the perimeter. Substituting a = 10.9 and p = 72, we get:
A = (1/2)(10.9)(72) = 394.56 square feet
Therefore, the area of the gazebo is 394.56 square feet.
c. To find the cost of the flooring, we need to multiply the area by the cost per square foot. Substituting A = 394.56 and the cost per square foot as $3, we get:
Cost = A($3/square foot) = 394.56($3/square foot) = $1,183.68
Rounding to the nearest hundred dollars, the cost of the flooring is $1,184. Therefore, the cost of the gazebo's flooring is $1,184.
#SPJ1
what is 5x + 1/10 * 10 if X= 10
Answers
Answer:
501
Step-by-step explanation:
Answer: 51
Step-by-step explanation:
Segments that join oppsoite vertices in a quadrilateral are called what
Answers
Answer:
Diagonal, I'm 90% sure it is at least!!
HELP! Someone! Anyone! Please help!

Answers
Factor completely, then place the answer in the proper location on the grid.
21a2-57a+ 30
Answers
Answer:
3 (7 a - 5) (a - 2)
Step-by-step explanation:
Factor the following:
21 a^2 - 57 a + 30
Factor 3 out of 21 a^2 - 57 a + 30:
3 (7 a^2 - 19 a + 10)
Factor the quadratic 7 a^2 - 19 a + 10. The coefficient of a^2 is 7 and the constant term is 10. The product of 7 and 10 is 70. The factors of 70 which sum to -19 are -5 and -14. So 7 a^2 - 19 a + 10 = 7 a^2 - 14 a - 5 a + 10 = a (7 a - 5) - 2 (7 a - 5):
3 a (7 a - 5) - 2 (7 a - 5)
Factor 7 a - 5 from a (7 a - 5) - 2 (7 a - 5):
Answer: 3 (7 a - 5) (a - 2)
H varies directly as L. If H = 15 when L = 30, determine H when L = 20A. Write the variation of the equation.B. Determine the value of the quantity indicated.
Answers
Answer:
A. The variation of the equation is
\(H=\frac{1}{2}L\)B. H is 10 when L is 20
Explanation:
Given that H varies directly as L, this can be written as:
\(H\propto L\)and defined as:
\(H=kL\)where k is constant.
To find the value of k, we use the given values H = 15 when L = 30
\(15=30k\)Divide both sides by 30
A.
\(k=\frac{15}{30}=\frac{1}{2}\)Therefore, the formula is:
\(H=\frac{1}{2}L\)B.
We want to determine H when L is 20
\(H=\frac{1}{2}(20)=10\)H is 10 when L is 20
Students on the baseball team and in the French club were asked how many pets they have. The results are shown.
Baseball Team: 0,0,0,1,1,1,1,1, 2, 2, 2,3,3,3,4
French Club: 0,0,1, 1, 1, 2, 2, 2, 2,3,3,3,3,4,6
What is the difference of the means of the two sets of data?
A. 0.6
B. 1
O C. 1.9
D. 2
Answers
Answer:
A
Step-by-step explanation:
The baseball teams total is 24, divided by the number of answers, 25, is 1.6.
The French Club’s total is 33, divided by the number of answers, 15, is 2.2.
2.2-1.6 is 0.6.
A publishing company conducted a survey asking readers whether they use e readers. Of the 3000 readers surveyed, 1954 said they read books on e reader. The approximate sample proportion is? Which means that? %of the readers surveyed don’t use e readers
Answers
Approximately 34.87% of the readers surveyed don't use e-readers.
To find the approximate sample proportion of readers who use e-readers, we divide the number of readers who said they read books on e-readers (1954) by the total number of readers surveyed (3000):
Approximate sample proportion = Number of readers who use e-readers / Total number of readers surveyed
Approximate sample proportion = 1954 / 3000 ≈ 0.6513
To express this as a percentage, we multiply the sample proportion by 100:
Approximate sample proportion as a percentage = 0.6513 × 100
= 65.13%
Therefore, the approximate sample proportion of readers who use e-readers is approximately 65.13%.
This means that approximately 65.13% of the readers surveyed use e-readers.
To determine the percentage of readers who don't use e-readers, we subtract the sample proportion from 100%:
Percentage of readers who don't use e-readers = 100% - 65.13%
= 34.87%
To learn more on Percentage click:
https://brainly.com/question/24159063
#SPJ1
What is the range of the function shown on the graph above

Answers
Answer:
d
Step-by-step explanation:
there isnt an arrow saying it keeps going past 10
Will mark brainliest.

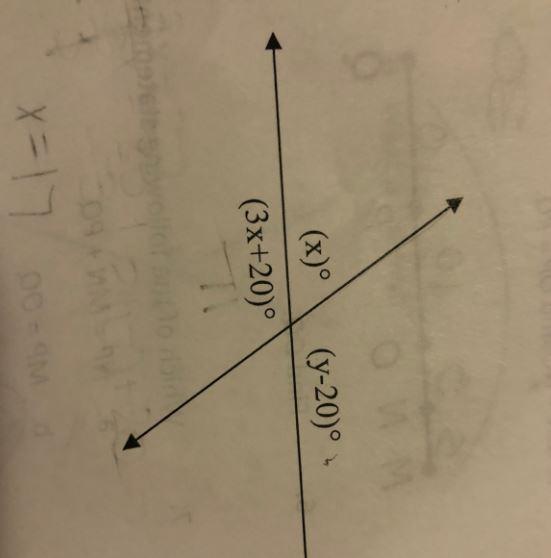
Answers
The solution is, the value of the variables are x = 40 and, y = 160.
Notice that "x" and "3x+20" are supplementary angles so their sum is 180°
(x) + (3x + 20) = 180
4x + 20 = 180
4x = 160
x = 40
To solve for "y", you have 2 options: either notice that "x" and "y-20" are supplementary angles so their sum is 180° or notice that "3x + 20" and "y - 20" are vertical angles so are equal to each other. I am going to solve using the first option because it is less work.
(x) + (y - 20) = 180°
40 + y - 20 = 180
y + 20 = 180
y = 160
Answer: x=40, y=160
The solution is, the value of the variables are x = 40 and, y = 160.
To learn more on angle click:
brainly.com/question/28451077
#SPJ1
complete question:
Find the value of each variable
one card is drawn from a pack of 52cards each of the 52 cards being equally likely to be drawn. what is the probability that the card drawn is a king?
Answers
The probability of drawing a king from a standard deck of 52 cards is 1/13.
In a standard deck of 52 playing cards, there are four kings: the king of hearts, the king of diamonds, the king of clubs, and the king of spades.
To find the probability of drawing a king, we need to determine the ratio of favorable outcomes (drawing a king) to the total number of possible outcomes (drawing any card from the deck).
The total number of possible outcomes is 52 because there are 52 cards in the deck.
The favorable outcomes, in this case, are the four kings.
Therefore, the probability of drawing a king is given by:
Probability = (Number of favorable outcomes) / (Number of possible outcomes)
= 4 / 52
= 1 / 13
Thus, the probability of drawing a king from a standard deck of 52 cards is 1/13.
This means that out of every 13 cards drawn, on average, one of them will be a king.
It is important to note that the probability of drawing a king remains the same regardless of any previous cards that have been drawn or any other factors.
Each draw is independent, and the probability of drawing a king is constant.
For similar question on probability.
https://brainly.com/question/7965468
#SPJ8
which ones is a function and not a function

Answers
Answer:
No,No,No,Yes,No,Yes
Step-by-step explanation:
Is 1.05 greater than or less than 1.3
Answers
The larger number is obtained as 1.3.
What is a Decimal number?A decimal number is the representation of a number in whole and a part. The whole is represented by an integer while the part is equivalent to a number divided by the order of 10.
The given decimal numbers are 1.05 and 1.3.
The decimal 1.3 can be written as 1.30.
Now, the two decimals can be compared as below,
1.05 and 1.30
Both the decimals have equal integer part.
Digit at tenths of 1.05 is 0 and for 1.30 is 3.
Since, 3 > 0.
⇒ 1.30 > 1.05
Hence, 1.3 is greater than 1.05.
To know more about decimal number click on,
brainly.com/question/4708407
#SPJ2
Convert the fractions into equivalent lowest term fraction, decimal number, and percent. 6/12, 2 6/8, 10/16
Answers
Answer:
7/9, 18/14,
Step-by-step explanation:
its mean i have answer for that
Help What do I put in the blank

Answers
Answer:
4 for the first box and 2*2*19 for the second.
Step-by-step explanation:
I did this lesson in 4th grade
Answer:
_4_ is not a prime number.
The correct prime factorization of 76 is 2, 2 ,19 .
Step-by-step explanation:
Find x in the diagram below

Answers
The value of the angle x is 30 degrees
How to determine the valueTo determine the value of the variable x, we need to know the triangle sum theorem.
The triangle sum theorem is a theorem in mathematics stating that the sum total of the interior angles in a triangle is equivalent to 180 degrees.
We should also note that angle at right angle is 90 degrees
Then, we have the angles written as;
90 degrees
2x degrees
x degrees
Equate the angles , we have;
2x + x + 90 = 180
collect the like terms, we have;
2x + x = 180 - 90
add or subtract the like terms, we have;
3x = 90
divide by the coefficient
x = 30
Learn more about triangles at: https://brainly.com/question/14285697
#SPJ1
What is the average rate of change of g over the interval -8<t<2?
Answers
A water park has pools, slides, and rides that, in total, make use of 6.9 × 105 gallons
of water. They plan to add a ride that would make use of an additional 85, 000
gallons of water. Use scientific notation to express the total gallons of water made use
of in the park after the new ride is installed.
Answer:
x10 gallons
Answers
Answer:
x10 gallons
Step-by-step explanation:
you said it
Which of the following equals sin A?
Ignore my answer.

Answers
Answer:
You are correct it is A. cos B
Step-by-step explanation:
Find the area of the figure pictured below.
15 yd
10 yd
17 yd
5 yd
A

Answers
First find the area of the square, then the triangle.
15 times 17 = 255 sq. yd
Triangle:
(5 times 5)/2 = 12.5 sq. yd
Your answer is 267.5 sq. yd
Hope this helps.
Which side of DEF is the longest?
A. DE
B. EF
C. D
D. Cannot be determine

Answers
EF
Please like my answer
Answer:
EF
This is just extra words
Select all of the shapes below which are rotations of shape X.

Answers
A,C,B,D,F,H are the rotations of the shape X given in the picture.
Rotations of shapes refer to the transformation of a shape around a fixed point called the center of rotation. This transformation involves rotating the shape by a certain angle while keeping the shape's size and shape consistent.
The angle of rotation determines how much the shape is rotated. It is measured in degrees or radians.
Properties of Rotations:
Rotations preserve the size and shape of the original shape.
Before and after the rotation, the distance between any two points on the shape and its centre of rotation remains constant.
The orientation of the shape may change, but its overall appearance remains unchanged.
Learn more about rotations:
https://brainly.com/question/30950864
#SPJ1
Find the y-intercept of the line that passes through the given point and has the given slope : (-2,-1); m=-3
Answers
Answer:
0, -7
Step-by-step explanation:
Answer:
The y intercept is -7
Step-by-step explanation:
-3x-7 is the equation that passes through (-2,-1)
