Solve 21.85 x (-6.2)
Answers
Answer:
= −135.47x
Step-by-step explanation:
^^^^^^^^^^^^^^^
Related Questions
(01.03 MC)
What is the domain of the rational function f(x)=
x²+x-20 -?
X-4x²-9x+36

Answers
The domain of the rational function in this problem is given as follows:
All real values except x = -3, x = 3, x = 4.
How to obtain the domain of the function?The domain of a function is the set composed by all the input values that the function accepts.
The function in this problem is a fraction, meaning that the denominator cannot be zero.
The denominator is given as follows:
x³ - 4x² - 9x + 36.
The roots of the denominator are given as follows:
x = -3, x = 3, x = 4.
Hence the domain is all real values except those, meaning that the second option is the correct option.
More can be learned about the domain of a function at https://brainly.com/question/10687170
#SPJ1
Eli is following this recipe to bake bread rolls.
He uses 500 g of flour.
How much of the other ingredients does he use?
Recipe: Makes 12 bread rolls
400 g flour
6 g salt
8 g yeast
40 mL oil
360 mL water
Answers
Answer:
7.5 g salt
10g yeast
50 ML oil
450 ML water
Step-by-step explanation:
You would do 1/4 of the amount of (insert ingredient amout) added to the total (insert ingredient amount)
Prove the following integration formula:
\(\displaystyle \int e^{au}\sin(bu)\, du=\frac{e^{au}}{a^2+b^2}(a\sin(bu)-b\cos(bu))+C\)
Answers
Answer:
See Explanation.
General Formulas and Concepts:
Pre-Algebra
Distributive PropertyEquality PropertiesAlgebra I
Combining Like TermsFactoringCalculus
Derivative 1: \(\frac{d}{dx} [e^u]=u'e^u\)Integration Constant CIntegral 1: \(\int {e^x} \, dx = e^x + C\)Integral 2: \(\int {sin(x)} \, dx = -cos(x) + C\)Integral 3: \(\int {cos(x)} \, dx = sin(x) + C\)Integral Rule 1: \(\int {cf(x)} \, dx = c \int {f(x)} \, dx\)Integration by Parts: \(\int {u} \, dv = uv - \int {v} \, du\)[IBP] LIPET: Logs, Inverses, Polynomials, Exponents, TrigStep-by-step Explanation:
Step 1: Define Integral
\(\int {e^{au}sin(bu)} \, du\)
Step 2: Identify Variables Pt. 1
Using LIPET, we determine the variables for IBP.
Use Int Rules 2 + 3.
\(u = e^{au}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dv = sin(bu)du\\du = ae^{au}du \ \ \ \ \ \ \ \ \ v = \frac{-cos(bu)}{b}\)
Step 3: Integrate Pt. 1
Integrate [IBP]: \(\int {e^{au}sin(bu)} \, du = \frac{-e^{au}cos(bu)}{b} - \int ({ae^{au} \cdot \frac{-cos(bu)}{b} }) \, du\)Integrate [Int Rule 1]: \(\int {e^{au}sin(bu)} \, du = \frac{-e^{au}cos(bu)}{b} + \frac{a}{b} \int ({e^{au}cos(bu)}) \, du\)Step 4: Identify Variables Pt. 2
Using LIPET, we determine the variables for the 2nd IBP.
Use Int Rules 2 + 3.
\(u = e^{au}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dv = cos(bu)du\\du = ae^{au}du \ \ \ \ \ \ \ \ \ v = \frac{sin(bu)}{b}\)
Step 5: Integrate Pt. 2
Integrate [IBP]: \(\int {e^{au}cos(bu)} \, du = \frac{e^{au}sin(bu)}{b} - \int ({ae^{au} \cdot \frac{sin(bu)}{b} }) \, du\)Integrate [Int Rule 1]: \(\int {e^{au}cos(bu)} \, du = \frac{e^{au}sin(bu)}{b} - \frac{a}{b} \int ({e^{au} sin(bu)}) \, du\)Step 6: Integrate Pt. 3
Integrate [Alg - Back substitute]: \(\int {e^{au}sin(bu)} \, du = \frac{-e^{au}cos(bu)}{b} + \frac{a}{b} [\frac{e^{au}sin(bu)}{b} - \frac{a}{b} \int ({e^{au} sin(bu)}) \, du]\)[Integral - Alg] Distribute Brackets: \(\int {e^{au}sin(bu)} \, du = \frac{-e^{au}cos(bu)}{b} + \frac{ae^{au}sin(bu)}{b^2} - \frac{a^2}{b^2} \int ({e^{au} sin(bu)}) \, du\)[Integral - Alg] Isolate Original Terms: \(\int {e^{au}sin(bu)} \, du + \frac{a^2}{b^2} \int ({e^{au} sin(bu)}) \, du= \frac{-e^{au}cos(bu)}{b} + \frac{ae^{au}sin(bu)}{b^2}\)[Integral - Alg] Rewrite: \((\frac{a^2}{b^2} +1)\int {e^{au}sin(bu)} \, du = \frac{-e^{au}cos(bu)}{b} + \frac{ae^{au}sin(bu)}{b^2}\)[Integral - Alg] Isolate Original: \(\int {e^{au}sin(bu)} \, du = \frac{\frac{-e^{au}cos(bu)}{b} + \frac{ae^{au}sin(bu)}{b^2}}{\frac{a^2}{b^2} +1}\)[Integral - Alg] Rewrite Fraction: \(\int {e^{au}sin(bu)} \, du = \frac{\frac{-be^{au}cos(bu)}{b^2} + \frac{ae^{au}sin(bu)}{b^2}}{\frac{a^2}{b^2} +\frac{b^2}{b^2} }\)[Integral - Alg] Combine Like Terms: \(\int {e^{au}sin(bu)} \, du = \frac{\frac{ae^{au}sin(bu)-be^{au}cos(bu)}{b^2} }{\frac{a^2+b^2}{b^2} }\)[Integral - Alg] Divide: \(\int {e^{au}sin(bu)} \, du = \frac{ae^{au}sin(bu) - be^{au}cos(bu)}{b^2} \cdot \frac{b^2}{a^2 + b^2}\)[Integral - Alg] Multiply: \(\int {e^{au}sin(bu)} \, du = \frac{1}{a^2+b^2} [ae^{au}sin(bu) - be^{au}cos(bu)]\)[Integral - Alg] Factor: \(\int {e^{au}sin(bu)} \, du = \frac{e^{au}}{a^2+b^2} [asin(bu) - bcos(bu)]\)[Integral] Integration Constant: \(\int {e^{au}sin(bu)} \, du = \frac{e^{au}}{a^2+b^2} [asin(bu) - bcos(bu)] + C\)And we have proved the integration formula!
Prove: \(\displaystyle \int e^a^u sin(bu)\ du = \frac{e^a^u}{a^2+b^2} (a \ sin(bu) - b \ cos(bu)) + C\)
Integration by parts formula: \(\displaystyle \int udv = uv - \int vdu\)
Find u, du, v, and dv for this function: \(\displaystyle \int e^a^u sin(bu)\)
\(\displaystyle u =e^a^u \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ v = -\frac{cos(bu)}{b} \\ du=ae^a^u \ du \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dv = sin(bu) \ du\)Plug these values into the IBP formula.
\(\displaystyle \int e^a^u sin(bu) \ du = e^a^u \cdot \frac{-cos(bu)}{b} - \int -\frac{cos(bu)}{b} \cdot ae^a^u \ du\)Multiply and simplify the factors. Factor the negative out of the integral.
\(\displaystyle \int e^a^u sin(bu) \ du = -\frac{e^a^u cos(bu)}{b} +\int \frac{a \ cos(bu) \ e^a^u}{b} \ du\)Factor out a/b from the integral.
\(\displaystyle \int e^a^u sin(bu) \ du = -\frac{e^a^u cos(bu)}{b} + \frac{a}{b} \int cos(bu) \ e^a^u \ du\)Now we are going to apply IBP to the function: \(\displaystyle \int cos(bu) \ e^a^u\) . Find u, du, v, and dv for this function.
\(\displaystyle u =e^a^u \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ v = \frac{sin(bu)}{b} \\ du=ae^a^u \ du \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ dv = cos(bu) \ du\)Plug these values into the IBP formula.
\(\displaystyle \int e^a^u cos(bu) \ du = e^a^u \cdot \frac{sin(bu)}{b} - \int \frac{sin(bu)}{b} \cdot ae^a^u \ du\)Multiply and simplify the factors.
\(\displaystyle \int e^a^u cos(bu) \ du = \frac{e^a^u \ sin(bu)}{b} - \int \frac{a \ sin(bu)\ e^a^u}{b} \ du\)Factor out a/b from the integral.
\(\displaystyle \int e^a^u cos(bu) \ du = \frac{e^a^u \ sin(bu)}{b} - \frac{a}{b} \int sin(bu)\ e^a^u} \ du\)Notice that we have the same integral we started with. Let's plug this integral into the original IBP we did.
\(\displaystyle \int e^a^u sin(bu) \ du = -\frac{e^a^u cos(bu)}{b} + \frac{a}{b} \big{[ }\frac{e^a^u sin(bu)}{b} - \frac{a}{b} \int sin(bu) \ e^a^u \ du \big{]}}\)Distribute a/b inside the parentheses.
\(\displaystyle \int e^a^u sin(bu) \ du = -\frac{e^a^u cos(bu)}{b} + \frac{a \ e^a^u sin(bu)}{b^2} - \frac{a^2}{b^2} \int sin(bu) \ e^a^u \ du\)Factor 1/b out of the right side of the equation.
\(\displaystyle \int e^a^u sin(bu) \ du = \frac{1}{b}\big{[} -e^a^u cos(bu)+ a \big{(}\frac{e^a^u sin(bu)}{b} \big{)} - \frac{a^2}{b} \int sin(bu) \ e^a^u \ du \big{]}\)Multiply both sides by b to get rid of 1/b.
\(\displaystyle b \int e^a^u sin(bu) \ du = -e^a^u cos(bu)+ a \big{(}\frac{e^a^u sin(bu)}{b} \big{)} - \frac{a^2}{b} \int sin(bu) \ e^a^u \ du\)Add the integral to both sides of the equation.
\(\displaystyle b \int e^a^u sin(bu) \ du + \frac{a^2}{b} \int sin(bu) \ e^a^u \ du= -e^a^u cos(bu)+ a \big{(}\frac{e^a^u sin(bu)}{b} \big{)}\)Factor the integral on the left side.
\(\displaystyle \int e^a^u sin(bu) \ du \ \big{(} b + \frac{a^2}{b} \big{)}= -e^a^u cos(bu)+ a \big{(}\frac{e^a^u sin(bu)}{b} \big{)}\)\(\displaystyle \big{(}b+\frac{a^2}{b} \big{)} = \frac{b^2+a^2}{b}\), so we can multiply both sides of the equation by \(\displaystyle \frac{b}{a^2+b^2}\).
\(\displaystyle \int e^a^u sin(bu) \ du = -e^a^u cos(bu)+ a \big{(}\frac{e^a^u sin(bu)}{b} \big{)} \big{(} \frac{b}{a^2+b^2} \big{)}\)Simplify the equation before multiplying everything by \(\displaystyle \frac{b}{a^2+b^2}\).
\(\displaystyle \int e^a^u sin(bu) \ du = \big{(}\frac{-e^a^u cos(bu) \ b + a \ e^a^u sin(bu)}{b} \big{)} \big{(} \frac{b}{a^2+b^2} \big{)}\)Multiply the two factors together. Notice that the two b's in the denominator and numerator, respectively, cancel out. We are left with:
\(\displaystyle \int e^a^u sin(bu) \ du = \big{(}\frac{-e^a^u cos(bu) \ b + a \ e^a^u sin(bu)}{a^2+b^2} \big{)}\)Factor \(\displaystyle e^a^u\) from the numerator.
\(\displaystyle \int e^a^u sin(bu) \ du = \big{(}\frac{e^a^u( -b \ cos(bu) \ + a \ sin(bu)}{a^2+b^2} \big{)}\)Split the numerator and denominator to make it appear the same as the original question.
\(\displaystyle \int e^a^u sin(bu) \ du = \frac{e^a^u}{a^2+b^2} \big{(} a \ sin(bu) - b \ cos(bu) \big{)}\)Since we are taking the integral of something, we can add a +C at the end to complete the problem.
\(\displaystyle \int e^a^u sin(bu) \ du = \frac{e^a^u}{a^2+b^2} \big{(} a \ sin(bu) - b \ cos(bu) \big{)} + C\)This is equivalent to the proof that we are given, therefore, we proved the integral correctly.
Pepe's science test scores for the semester are 94, 69, 74, 96, He wants to get all of his test score to be an average of at least eighty eight. What score must he get on his fifth test? (Enter a numeric value)
Answers
Answer:
Step-by-step explanation:
1. Find the mean
94 + 69+74+96 = 333
Divide 333 by 4 = 83.25
Subtract 83.35 from 88
Answer : 4.75
Now follow the next steps
333/4= 83.25
Average is 83.25
88+88=176
176-83.25=92.75
Which means he need to get at least 93 marks for an average of 88.
Answer with at least 3-4 sentences. No fake answers lots of points
The discriminant is a way to determine the number of solutions a quadratic would have WITHOUT solving it. What is the discriminant of the below quadratic and what does that mean?
x2−4x+5=0
Answers
Answer:
4
Step-by-step explanation:
Calculation of the discriminant of the polynomial : x⋅2−4⋅x+5
1. Applying the formula to calculate the discriminant Δ=b2−4⋅a⋅c with : a=0, b=−2,c=5
2. Δ=(−2)2−4⋅(0)⋅(5)=4=4
3. The discriminant of the polynomial x⋅2−4⋅x+5 is equal to 4
What is this please I need help
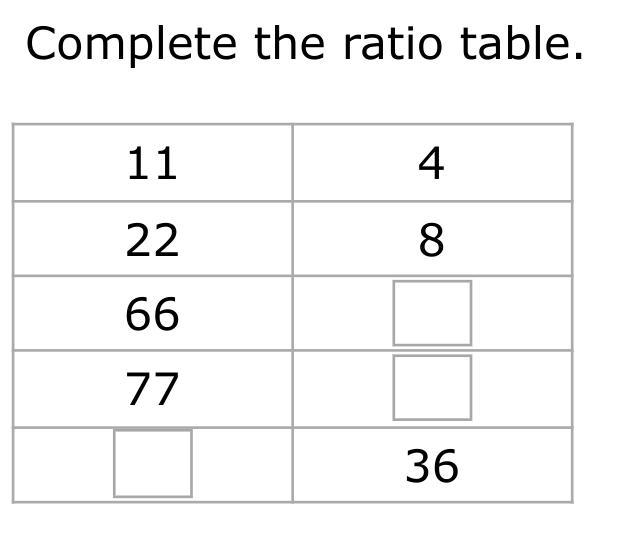
Answers
Answer:
Box 1= 24 Box 2= 28 Box 3= 99( Not sure about box 3, and sorry if it is wrong)
Step-by-step explanation:
A salesperson receives a base salary of $32,000 and a commission of 15% of the total sales for the year.
a. Write a linear equation that shows the salesperson's total income based on total sales of x dollars.
b. Identify the slope and the y-intercept with units.
c. If the salesperson sells $150,000 worth of merchandise, what is her total income for the year including her base salary?
d. How much would she have to sell if she wants to earn $60,000 per year?
Answers
The salesperson would need to sell $186,667 worth of merchandise to earn $60,000 per year, including her base salary.
a. The linear equation representing the salesperson's total income (I) based on total sales of x dollars is:
I = 0.15x + 32,000
b. In this equation, the slope (representing commission rate) is 0.15 (or 15%) and has a unit of dollars per dollar of sales. The y-intercept (representing base salary) is 32,000 and has a unit of dollars.
c. To calculate the total income for the year when the salesperson sells $150,000 worth of merchandise:
I = 0.15(150,000) + 32,000
I = 22,500 + 32,000
I = $54,500
The total income for the year, including her base salary, is $54,500.
d. To determine how much the salesperson needs to sell to earn $60,000 per year:
60,000 = 0.15x + 32,000
28,000 = 0.15x
x = 28,000 / 0.15
x = $186,666.67
The salesperson would need to sell approximately $186,666.67 worth of merchandise to earn $60,000 per year.
a. The linear equation that shows the salesperson's total income based on total sales of x dollars is:
income = 0.15x + 32000
b. The slope of the equation is 0.15 and represents the commission rate (15%) earned on each dollar of sales. The y-intercept of the equation is 32000 and represents the base salary.
c. If the salesperson sells $150,000 worth of merchandise, her total income for the year including her base salary would be:
income = 0.15(150000) + 32000
income = 22500 + 32000
income = $54,500
d. To earn $60,000 per year, the salesperson would need to solve for x in the equation:
income = 0.15x + 32000
60000 = 0.15x + 32000
28000 = 0.15x
x = $186,667
Therefore, the salesperson would need to sell $186,667 worth of merchandise to earn $60,000 per year, including her base salary.
Learn more about salary here: brainly.com/question/14371457
#SPJ11
FILL IN THE BLANK. In a(n) _____, team members prepare to lunge at each other to achieve their objectives.a. adaptationb. scrumc. resequencing sessiond. pool
Answers
For the purpose of content marketing, the strategies portion of strategic planning focuses on how content marketing can help achieve certain goals and objectives.
This is because strategies are the overarching plans that guide the actions and decisions of a content marketing program.
A content marketing strategy defines the target audience, key messages, channels, and metrics for success. It outlines how content will be created, distributed, and measured in order to achieve specific business objectives.
The tactics portion of strategic planning is more focused on the specific actions and initiatives that will be taken to execute the strategy. Tactics might include things like social media campaigns, email marketing, webinars, or video production. While tactics are important, they should always be guided by the overarching strategy in order to ensure that they are aligned with business goals and objectives.
Messages are the specific pieces of content that are created as part of a content marketing program. While messages are important for engaging the audience and driving action, they are not the primary focus of strategic planning. Finally, situational analysis is an important step in the planning process, but it is not specific to content marketing. A situational analysis is a broad assessment of the business environment and competitive landscape, which is used to inform overall business strategy.
Learn more about content marketing here:
brainly.com/question/25778296
#SPJ1
complete question:
For the purpose of content marketing, the ______ portion of strategic planning focuses on how content marketing can help achieve certain goals and objectives.A) strategiesB) tacticsC) messagesD) situational analysis
Please answer the both questions in the photos below ( will mark brainliest if available + 30p )


Answers
The classification of the system of linear equations 4x + y = 4 and y = -4x + 4 is: consistent and independent. The Option B is correct.
Why is the equation's classification consistent independent?We have a consistent independent equation when a system of linear equations has exactly one solution. When this occurs, the graphs of the system's lines cross at exactly one point.
For our question, we can start by rearranging the first equation to isolate y:
\(4x + y = 4\\y = -4x + 4\)
We can see that the second equation is already in the form y = mx + b, where m is the slope and b is the y-intercept. So we can identify that the slope of the second equation is -4 and the y-intercept is 4.
Now we can compare the slopes and y-intercepts of the two equations to determine the classification of the system of equations:
If the slopes are the same and the y-intercepts are different, the system is inconsistent and there is no solution.If the slopes are different, the system is consistent and there is a unique solution.If the slopes are the same and the y-intercepts are the same, the system is consistent and there are infinitely many solutions.In this case, we can see that the slopes of the two equations are different (-4 and 0) and the y-intercepts are the same (4). Therefore, the system is consistent and there is a unique solution. So the classification of the system of linear equations 4x + y = 4 and y = -4x + 4 is: consistent and independent
Read more about consistent independent equation
brainly.com/question/26523945
#SPJ1
The main goal of a personal budget is to
A. have income equal expenses
B. have expenses be greater than income
C. have income be greater than expenses
D. create personal savings
Answers
The main goal of a personal budget is to have income be greater than expenses
What is budget?
Budget is an estimate of income and expenditure for a set period of time. It gives a spending plan based on current and future income and expenses.
A personal (household) budget compares your income and expenses for a defined period.
The main goal of a personal budget is to have income be greater than expenses
Find out more on budget at: https://brainly.com/question/6663636
#SPJ1
What number makes the equation?
__÷6 = 30
Answers
Answer:
The number needed is 180
Step-by-step explanation:
Have a nice day! I hope this helps!
Question is in picture

Answers
Answer:
The first one
Step-by-step explanation:
4 x 4 = 16 16 x 4= 64.
The solutions to the equation -4|x + 9| = -8 are:
7, 11
7, -11
-7, 11
-7, -11
Answers
Answer:
option 4
Step-by-step explanation:
Given Equation :-
=> -4| x + 9 | = -8
To FinD :-
=> Solution of the equation .
Solving it :-
=> -4| x + 9 | = -8
=> | x + 9 | = -8/-4
=> |x + 9| = 2
=> ( | x + 9 | )² = 2²
=> x + 9 = ±2
=> x = -9 +2 , -9-2
=> x = - 7 , -11
Option 4 is correct.
Answer:
x = - 7 , - 11
Step-by-step explanation:
\(-4 | x +9| = - 8\\\\\frac{-4}{-4} |x+9| = \frac{-8}{-4}\\\\1 | x+9| = 2\\\\x+9 = - 2\ , x + 9 = 2\\\\x + 9 - 9 = - 2 - 9 , \ x + 9 - 9 = 2 - 9\\\\x + 0 = - 1 1 \ , \ x + 0 = - 7\\\\x = -11 \ , \ x = - 7\)
prove that if f(x) has no factor of the form x^2 ax b, then it has no quadratic over zp
Answers
We can conclude that if f(x) has no factor of the form x^2 ax b, then it has no quadratic over zp.
To prove that if f(x) has no factor of the form x^2 ax b, then it has no quadratic over zp, we need to first understand what a quadratic is. A quadratic is a polynomial of degree two, which means it can be written in the form ax^2 + bx + c. Now, if f(x) has no factor of the form x^2 ax b, then it means that it cannot be written in this form.
To understand this better, let's consider the case of f(x) having a quadratic factor over zp. This would mean that we can write f(x) as g(x)h(x), where g(x) and h(x) are both quadratic polynomials over zp. Since a quadratic polynomial can always be factored as (x - r)(x - s), where r and s are the roots of the polynomial, it follows that g(x) and h(x) can each be factored as (x - r1)(x - r2) and (x - s1)(x - s2) respectively.
Now, if we multiply these factors out, we get:
f(x) = (x - r1)(x - r2)(x - s1)(x - s2)
= x^4 - (r1 + r2 + s1 + s2)x^3 + (r1r2 + r1s1 + r1s2 + r2s1 + r2s2 + s1s2)x^2 - (r1r2s1 + r1r2s2 + r1s1s2 + r2s1s2)x + r1r2s1s2
This is a polynomial of degree four, which means that it has a factor of the form x^2 ax b. But we assumed that f(x) has no factor of this form, which means that our assumption that f(x) has a quadratic factor over zp is false.
Therefore, we can conclude that if f(x) has no factor of the form x^2 ax b, then it has no quadratic over zp.
Visit here to learn more about quadratic:
brainly.com/question/22364785
#SPJ11
NEEP HELP ASAP
What is the area of the hexagon?
Answers
Answer:
( n - 2 ) × 180°
I hope it help

help asap (like right now )

Answers
Answer:
B) Yes, because the slope is \(-\frac{25}{3}\) and the zero is (12, 0)
Step-by-step explanation:
From inspection of the graph:
y-intercept = (0, 100)Two points: (3, 75) and (6, 50)\(\sf slope\:(m)=\dfrac{change\:in\:y}{change\:in\:x}=\dfrac{50-75}{6-3}=-\dfrac{25}{3}\)
Therefore, the equation of the line in slope-intercept form y = mx + b
(where m is the slope and b is the y-intercept) is:
\(y=-\dfrac{25}{3}x+100\)
To find the zero (when y = 0), set the equation to zero and solve for x:
\(\implies -\dfrac{25}{3}x+100=0\)
\(\implies \dfrac{25}{3}x=100\)
\(\implies 25x=300\)
\(\implies x=12\)
Therefore, the zero is at (12, 0)
Therefore, the graph does represent the function because the slope is \(-\frac{25}{3}\) and the zero is at (12, 0)
The equation is P= 6s represents the perimeter P of a regular hexagon with side length s. What is the perimeter of a regular hexagon with side length as 5 mm?
Answers
Answer:
30
Step-by-step explanation:
a recent survey found that out of a random sample of 150 drivers, 100 of them wear seatbelts. what is the 95onfidence interval for the proportion p of drivers that do not wear seatbelts?
Answers
The 95% CI for proportion of driver that do not wear seat belt is 0.255 < p < 0.405.
What is Confidence interval?
A confidence interval (CI) is a range of estimates for an unknown parameter in frequentist statistics. The 95% confidence level is the most popular, however other levels, such 90% or 99%, are occasionally used when computing confidence intervals.
As given,
n = 150 = drivers
x = 100 = wear seat belts.
We have to find 95% confidence interval for proportion P that do not wear seat belt.
From 150 we have 100 wear seat belts
Not wear seat belt = 150 - 100
Not wear seat belt = 50
P = 50/150
P = 0.33
95% confidence interval for P is
CI = (P - zα/2√(P(1 - P)/n), P + zα/2√(P(1 - P)/n))
For 95% CI, zα/2 = 1.96
Substitute values,
CI = (0.33 - 1.96√(0.33(1 - 0.33)/150), 0.33 + 1.96√(0.33(1 - 0.33)/150))
CI = (0.33 - 0.075, 0.33 + 0.075)
CI = (0.255, 0.405)
Therefore 95% CI for proportion of driver that do not wear seat belt is 0.255 < p < 0.405.
To learn more about Confidence interval CI from the given link.
https://brainly.com/question/20309162
#SPJ4
\(\sf \sqrt{12} \times \sqrt{12}\)
Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
The Equivalent value is ~
\( \boxed{12}\)
\( \large \boxed{ \mathfrak{Step\:\: By\:\:Step\:\:Explanation}}\)
Let's solve ~
\( \sqrt{12} \times \sqrt{12} \)\( \sqrt{2 \times 2 \times 3} \times \sqrt{2 \times 2 \times 3} \)\(2 \sqrt{3} \times 2 \sqrt{3} \)\(4 \sqrt{3 \times 3} \)\(4 \times 3\)\(12\)what is the answer to 3s=45?
Answers
3s=45
3s/3=45/3
S=15
You have to divide both sides
two years ago, a baby elephant was 11 feet shorter than its mother. However it grew 3 feet and bow its mother is only twice its size. How big was the baby elephant two years ago?
Answers
Answer: 11 feet shorter than it’s mother.
Step-by-step explanation:
Key phrase, “Two years ago, a baby elephant was 11 feet shorter than it’s mother”. Saying the only reference as if 2 years, being 11 ft shorter. As well as there being no starting unit to work from to reference fire but the animals actually are, thus therefore a trick question. It never tells you what their size is, only unnecessary extra info without giving a starting unit for reference. Or to put it simply, it only refers to to what it was and has became, and doesn’t refer to what it ever is.
Maximum Marks: 5 Given the total cost function TC=100Q−Q 2
+0.3Q 3
Where Q= rate of output and TC= total cost, determine a) The marginal and average cost functions. (2 Marks) b) The rate of output that results in minimum average cost. ( 3 Marks)
Answers
a) To find the marginal cost, we need to find the derivative of the total cost function with respect to the rate of output (Q).
TC = 100Q - Q² + 0.3Q³
Marginal cost (MC) = dTC/dQ
= d/dQ(100Q - Q² + 0.3Q³)
= 100 - 2Q + 0.9Q²
To find the average cost, we need to divide the total cost by the rate of output (Q).
Average cost (AC) = TC/Q
= (100Q - Q² + 0.3Q³)/Q
= 100 - Q + 0.3Q²
b) To find the rate of output that results in minimum average cost, we need to find the derivative of the average cost function with respect to Q. Then, we set it equal to zero and solve for Q.
AC = 100 - Q + 0.3Q²
dAC/dQ = -1 + 0.6Q
= 0-1 + 0.6Q
= 00.6Q
= 1Q
= 1/0.6Q
≈ 1.67
Therefore, the rate of output that results in minimum average cost is approximately 1.67.
Learn more about Marginal Cost:
https://brainly.com/question/30165613
#SPJ11
Using the chart in your text, calculate how many hours per week you should ideally spend studying if you have one three-credit class that is less demanding, two three-credit classes that are typically demanding, and one four- credit class that is very challenging.
Answers
Using the same guideline, for a four-credit class, you would ideally spend:
4 credits * 2-3 hours/credit = 8-12 hours per week.
it is suggested that students allocate around 2-3 hours of study time per credit hour per week for a college-level course. However, the actual study time required may vary based on individual learning styles, prior knowledge, and the specific requirements set by professors or institutions.
Let's apply this general guideline to your scenario:
One three-credit class that is less demanding:
Assuming 2-3 hours of study per credit hour, for a three-credit class, you would ideally spend:
3 credits * 2-3 hours/credit = 6-9 hours per week.
Two three-credit classes that are typically demanding:
Similarly, for each of the two three-credit classes, you would spend:
3 credits * 2-3 hours/credit = 6-9 hours per week.
Since you have two such classes, the total time would be:
2 * (6-9) hours = 12-18 hours per week.
One four-credit class that is very challenging:
Using the same guideline, for a four-credit class, you would ideally spend:
4 credits * 2-3 hours/credit = 8-12 hours per week.
Learn more about credit from
https://brainly.com/question/30682995
#SPJ11
What is the approximate volume of this sphere?
Don't forget to use the formula: V=43πr3
A 392.5 cm3
B 523.3¯ cm3
C 3,140 cm3
D 4,186.6¯ cm3

Answers
Answer: The correct answer is B. 523.3...cm^3
Step-by-step explanation:
4/3*pi*r^3 is the formula
first, divide the diameter by 2 to get the radius, now, you will begin solving.
4/3*5^3*3.14
5*5*5=125
4/3*125*3.14
125*3.14=392.5
4/3*392.5
523.3...
help meee 5774 + 252 - 2586 ×35
Answers
Answer:
The answer is -84,484
Step-by-step explanation:
using Bodmas
multiplication first
5774+252-(2586×35)
5774+252-90510
6026-90510
-84,484
name the line ........

Answers
Answer:
Step-by-step explanation:
l is line. It has no beginning and end point.
AB is a ray. It has a beginning point and has no end point.
CD is a segment and it has both beginning and end point.
∠1 is an angle.
a, b are parallel lines and t is transversal.
A spherical snowball is melting in such a way that its radius is decreasing at a rate of 0.2 cm/min. At what rate is the volume of the snowball decreasing when the radius is 16 cm. (Note the answer is a positive number).
Answers
The rate at which the volume of the snowball is decreasing when the radius is 16 cm is approximately 204.8π cm^3/min.
To find the rate at which the volume of the snowball is decreasing, we need to use the derivative of the volume with respect to time. Let's denote the volume of the snowball as V(t) and the radius as r(t).
The formula for the volume of a sphere is V = (4/3)πr^3. We can differentiate this formula with respect to time t using the chain rule:
dV/dt = dV/dr * dr/dt.
The derivative of the volume with respect to radius, dV/dr, is given by:
dV/dr = (4/3)π * 3\(r^2\) = 4π\(r^2.\)
The given information tells us that the radius is decreasing at a rate of dr/dt = -0.2 cm/min.
Now we can substitute the values into the equation:
dV/dt = 4π\(r^2\) * dr/dt
= 4π\((16)^2\) * (-0.2)
= -204.8π cm^3/min.
Since we are asked for the rate of decrease in volume, the answer is a positive number. Thus, the rate at which the volume of the snowball is decreasing when the radius is 16 cm is approximately 204.8π cm^3/min.
Note: π is an irrational number approximately equal to 3.14159, so the final answer can be approximated as 643.06 cm^3/min.
For more such questions on rate visit:
https://brainly.com/question/119866
#SPJ8
One positive integer is 1 greater than 3 times another positive integer. If the product of the two integers is 154, then what is the sum of the two integers?
Answers
Answer:
29
Step-by-step explanation:
Let the smaller integer be x.
The other integer is 1 greater than 3 times x, or 3x + 1.
The product is 154.
x(3x + 1) = 154
3x^2 + x - 154 = 0
157 = 2 * 7 * 11
14 * 11 = 154
22 * 7 = 154
(3x + 22)(x - 7) = 0
3x + 22 = 0 or x - 7 = 0
3x = -22 or x = 7
x = -22/3 or x = 7
-22/3 is not a positive integer, so we discard that solution.
The smaller integer is 7.
3x + 1 = 3(7) + 1 = 22
The greater integer is 22.
The sum of the integers is 7 + 22 = 29
Answer: 29
Step-by-step explanation:
find the intercepts of y=5
Answers
Answer:
y -intercept is 5 and the x -intercept is undefined
Step-by-step explanation:
The graph is a horizontal line that is parallel to the x-axis and there is no points on the line that are on the x-axis.
if the saving rate is 1 (i.e., s = 1), we know that
Answers
If the saving rate is 1, it means that an individual or an economy saves their entire income and spends nothing. This implies that the consumption rate is 0, and all income is being saved.
In this scenario, the investment rate is equal to the saving rate, as there is no consumption spending. Therefore, the economy is investing all of its income in capital goods and not in consumption goods. This approach may result in high economic growth in the future due to the increased production capacity of the economy. However, in the short term, it may lead to a decrease in consumer demand and a decrease in output and employment in sectors producing consumer goods.
To learn more about investment : brainly.com/question/15105766
#SPJ11