Study this model of earth, the moon, and the sun. then answer the questions.
in this model, number 1 represents
v
number 2 represents
and number 3 represents
reset
next
Answers
In the given model of Earth, the Moon, and the Sun, number 1 represents the Moon, number 2 represents Earth, and number 3 represents the Sun.
Based on the provided information, we can interpret the model as a representation of the positions of the Moon, Earth, and the Sun. In this context, number 1 corresponds to the Moon, number 2 represents Earth, and number 3 represents the Sun.
The Moon is the natural satellite orbiting around Earth, and it plays a significant role in various natural phenomena such as tides. Earth, represented by the number 2, is the planet we inhabit and is located between the Moon and the Sun. The Sun, represented by the number 3, is the star at the center of our solar system, providing light, heat, and energy to Earth.
By understanding the roles and positions of the Moon, Earth, and the Sun in this model, we can better comprehend their relationships and interactions within the context of the solar system.
To learn more about solar system click here: brainly.com/question/32240766
#SPJ11
Related Questions
Convert the decimal numeral 1407 to base 6
Answers
Answer:
Therefore, the base-6 representation of 1407 is 1303.
Step-by-step explanation:
To convert the decimal numeral 1407 to base 6, we can use the following steps:
Divide 1407 by 6 and store the quotient and the remainder.
Repeat the division process with the quotient until the quotient is 0.
Write down the remainders in the reverse order to get the base-6 representation of 1407.
So, the steps would look like this:
1407 ÷ 6 = 234 with a remainder of 3
234 ÷ 6 = 39 with a remainder of 0
39 ÷ 6 = 6 with a remainder of 3
6 ÷ 6 = 1 with a remainder of 0
1 ÷ 6 = 0 with a remainder of 1
Writing down the remainders in the reverse order, we get: 1407(10) = 1303_6.
Therefore, the base-6 representation of 1407 is 1303.
The owner of a local restaurant surveyed her staff on their preference of uniform color. The results are displayed in the table below. Which pair of samples is most representative of the preference of all the staff? VX Sample 3 Beige Blue Black Sample 1 3 7 10 Uniform Color Survey Sample 2 Beige 12 Blue 15 Black Beige Blue Black 15 18 O Sample 1 and sample 2 are most representative because they are the same size. O Sample 1 and sample 3 are most representative because the relationship between preferences is consistent. Sample 2 and sample 3 are most representative because the samples show a greater variability in preferences. None of the samples are representative because none of the values remain constant.
Answers
Answer:
The answer is B
Step-by-step explanation:
I just took the quiz on edge 2021 the answer is B
Answer:
B is tha answer
Step-by-step explanation:
If you have a sample size of 16 and a population standard deviation of 40, what is your standard error of the mean
Answers
The standard error of the mean is 10.
The standard error of the mean (SEM) is calculated by dividing the
population standard deviation (σ) by the square root of the sample size (n):
SEM = σ / √n
In this case, the population standard deviation is 40 and the sample size is 16.
Substituting these values into the formula, we get:
SEM = 40 / √16
SEM = 40 / 4
SEM = 10
Therefore, the standard error of the mean is 10.
for such more question on standard error
https://brainly.com/question/22377370
#SPJ11
The product of two numbers is 5430. If one of the numbers is 15 what is the other
number?
43
Answers
Answer:
362
Step-by-step explanation:
15xy=5430...therefore 5430divided by 15 is 362...so 362x15 their product is 5430
Help pleaseeeee it’s dueeeeee
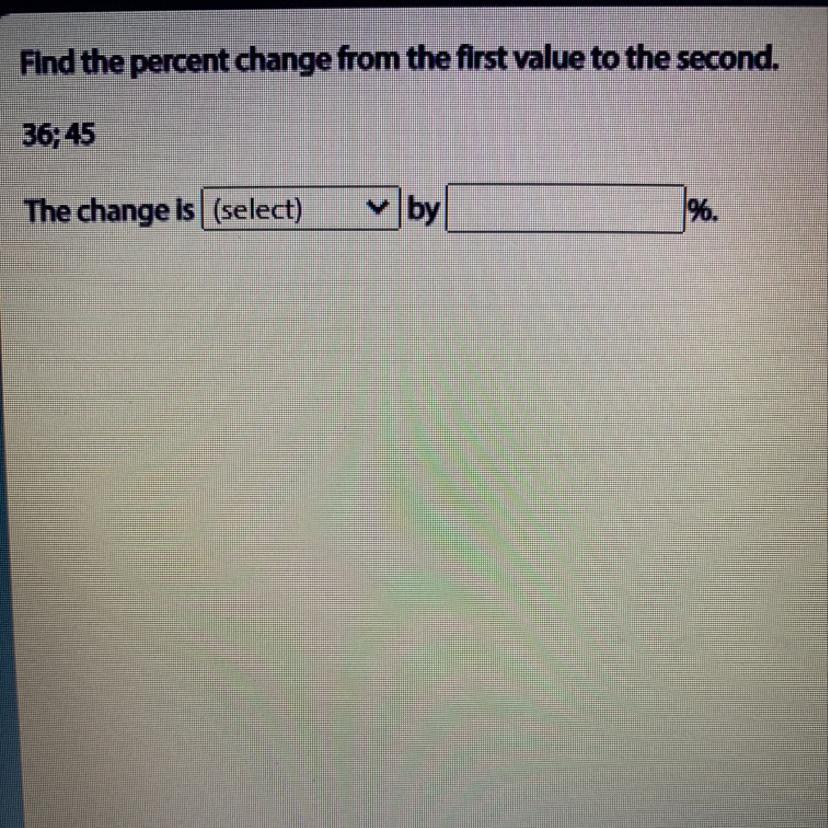
Answers
Answer:
The change is increased by 80%.
Step-by-step explanation:
Divide 36 by 45. This gives you 0.8. Divide 36 by 0.8 and multiply 45 by 0.8 to check your answer. So, it is increased by 80%. To find out how percents change, divide the first number by the second number. Then, take the decimal and move the decimal point over to the right two spaces, or multiply the entire number by 100.
The LIGO experiment, which historically detected gravita- tional waves for the first time in September 2015, uses a pair of highly sensitive Michelson interferometers. These have arms that are 4.00 km long and use powerful Nd:Yag lasers with 1064 nm wavelength. The beams traverse the arms both ways 280 times before recombining, which effectively lengthens the arm length to 1120 km. The devices are tuned so that the beams destructively interfere when they recom- bine if no gravitational wave is present. (a) The beam has a power of 100 kW, concentrated into an area of a square centimeter. Calculate the amplitude of the electric field in the beam. (b) LIGO can detect a gravitational wave that temporarily lengthens one arm by the minus- cule amount of 10-18 m! When this happens, the beams combine with a phase difference of p d. Estimate the shift d in radians. Note that the phase difference accumulates during both traversals of each round trip. (c) Use Eq. (35.7) to estimate the sensitivity of the photodetector in terms of the minimal electric field strength needed to detect a gravi- tational wave.
Answers
To calculate the amplitude of the electric field in the LIGO beam, we divide the power of 100 kW by the area of a square centimeter.
(a) The amplitude of the electric field in the LIGO beam can be calculated using the formula:
Amplitude of electric field = √(Power / Area)
Converting the power of 100 kW to 100,000 W and the area of a square centimeter to square meters:
Amplitude of electric field = √(100,000 / 0.0001) = √(10^9) = 10^4 V/m
Therefore, the amplitude of the electric field in the LIGO beam is 10,000 V/m.
(b) The phase shift caused by a gravitational wave temporarily lengthening one arm by 10^-18 m can be estimated using the formula:
Phase shift = (2π * d) / λ
Where d is the change in arm length and λ is the wavelength of the laser. In this case, the effective arm length is 1120 km, which is equivalent to 1.12 x 10^6 m, and the laser wavelength is 1064 nm, or\(1.064 x 10^-6 m.\)
Phase shift =\((2π * 10^-18) / (1.064 x 10^-6) = 2π * 10^-12 radians\)
Therefore, the estimated phase shift caused by the gravitational wave is approximately\(6.28 x 10^-12\) radians.
(c) Using Eq. (35.7), the sensitivity of the photodetector can be estimated by relating the minimal electric field strength required to detect a gravitational wave to the phase shift:
Minimal electric field strength = (λ * Amplitude of electric field) / (4π * d)
Substituting the values obtained:
Minimal electric field strength = \((1.064 x 10^-6 * 10^4) / (4π * 10^-12)\)
Simplifying the equation:
Minimal electric field strength = 8.49 x \(10^7\) V/m
Therefore, the estimated sensitivity of the photodetector is approximately 8.49 x \(10^7\) V/m, indicating the minimal electric field strength needed to detect a gravitational wave.
Learn more about divide here:
https://brainly.com/question/15381501
#SPJ11
jan is thinking of a positive integer. her integer has exactly 16 positive divisors, two of which are 12 and 15. what is jan's number?
Answers
Jan's number is 12.
To find Jan's number, we need to determine a positive integer that has exactly 16 positive divisors and includes both 12 and 15 as divisors.
Let's consider the prime factorizations of 12 and 15:
12 = 2^2 * 3
15 = 3 * 5
From these prime factorizations, we can see that the common factor between 12 and 15 is 3.
Now, to have exactly 16 positive divisors, the number should be in the form of \(p^a \times q^b \times r^c\), where \(p\), \(q\), and \(r\) are distinct prime numbers, and \(a\), \(b\), and \(c\) are positive integers.
Since 12 has 2^2 * 3 in its prime factorization and 15 has 3 * 5, we can construct the number by considering these factors:
The number will have 2 raised to the power of 2 because it needs to have 12 as a divisor. So far, we have \(2^2\).
Next, we need to include 3 raised to some power. Since 12 already has 3 in its factorization, we don't need to include an additional 3. Thus, we still have \(2^2\) for this part.
Finally, we need to include 5 raised to some power to account for 15 as a divisor. Since 15 already has 5 in its factorization, we don't need to include an additional 5.
Putting it all together, the number that satisfies the conditions is \(2^2 \times 3^1 \times 5^0 = 4 \times 3 \times 1 = 12\).
Therefore, Jan's number is 12.
To know more about divisors , refer here :
https://brainly.com/question/26086130#
#SPJ11
pls help asap if you can!!!

Answers
The statement that best proves that <XWY ≅ <ZYW is that two parallel lines are cut by a transversal, then the alternate interior angles are congruent
How to determine the statementTo determine the correct statement, we need to know the properties of a parallelogram.
These properties includes;
Opposite sides are parallel. Opposite sides are congruent. Opposite angles are congruent. Same-Side interior angles (consecutive angles) are supplementary. Each diagonal of a parallelogram separates it into two congruent triangles.The diagonals of a parallelogram bisect each other.Learn more about parallelogram at: https://brainly.com/question/10744696
#SPJ1
onsider the following production function: y = F(L, K) = 4L3 K} = where L and K are the amount of labour and capital used in the production process, and y is the output. Throughout this question, the output price p is 3 and the rental rate of capital r is 1. We will first consider a firm in the short run, where the amount of capital is fixed at K = 64. The fixed cost is therefore 64. = (a) (Level A) Is there diminishing returns to labour? Explain. (b) (Level A) Suppose the wage rate w is 1. Find the profit-maximising choice of L. Calculate the profit-maximising output level and the maximised profit. (There is no need to check the second order condition but of course you can check if you want to.) (c) (Level A) Now suppose w increases to 2. Find the profit-maximising choice of L. Calculate the profit-maximising output level and the maximised profit. (There is no need to check the second order condition.) You can leave your answers in square roots. (d) (Level A) What is the change in L when w increases from 1 to 2 in the short run? You can leave your answers in square roots.
Answers
Yes, there are diminishing returns to labor in the given production function.
What is the profit-maximizing choice of labor and the resulting output and profit level when the wage rate is 1?
There are diminishing returns to labor in the given production function. As more units of labor (L) are added while holding capital (K) constant, the increase in output (y) becomes smaller and smaller. This is indicative of diminishing marginal product of labor.
When the wage rate (w) is 1 and the capital (K) is fixed at 64, the profit-maximizing choice of labor (L) can be found by equating the marginal product of labor (MPL) to the wage rate. In this case, MPL = 12L^2K.
Setting MPL = w, we have 12L^2K = 1. Substituting K = 64, we get 12L^2 * 64 = 1. Solving for L, we find L ≈ 0.0917.
The profit-maximizing output level (y) can be calculated by substituting the values of L and K into the production function. Thus, y = 4L^3K = 4(0.0917)^3 * 64 ≈ 0.026.
The maximized profit can be determined by subtracting the total cost (TC) from the total revenue (TR). Since the fixed cost is given as 64, TC = 64 + wL = 64 + 1(0.0917) ≈ 64.092. TR is the product of the output level and the price, which is 0.026 * 3 = 0.078.
Profit = TR - TC ≈ 0.078 - 64.092 ≈ -63.014.
Diminishing returns to labor imply that as more labour is employed while holding other factors constant, the incremental increase in output becomes smaller. In the given production function, this phenomenon is observed. In the short run, with a fixed capital level of 64, we determine the profit-maximizing choice of labour (L) when the wage rate (w) is 1. By equating the marginal product of labour (MPL) to the wage rate, we find L ≈ 0.0917. Substituting this value into the production function, we calculate the profit-maximizing output level as y ≈ 0.026. The maximized profit is determined by subtracting the total cost (TC) from the total revenue (TR), resulting in a profit of approximately -63.014. This analysis helps understand the relationship between input choices, output levels, and profit optimization in the short run.
Learn more about labor
brainly.com/question/984683
#SPJ11
What is function and not function?
Answers
Answer: A function is a relation between domain and range such that each value in the domain corresponds to only one value in the range. Relations that are not functions violate this definition. They feature at least one value in the domain that corresponds to two or more values in the range.
Step-by-step explanation:
See photo to answer!

Answers
The length of AB of the triangle is 13 units.
How to find the side of a triangle?The side AB of the triangle can be found using cosine law,
Therefore,
c² = a² + b² - 2ab cos C
c² = 7² + 8² - 2 × 7 × 8 cos 120
c² = 49 + 64 - 112 cos 120
c²= 113 - (-56)
c² = 113 + 56
c² = 169
c = √169
c = 13 units
Therefore, the value of AB is 13 units
learn more on triangle here: https://brainly.com/question/3642070
#SPJ1
If log3=0.4771 and log2=0.3010,Find the value of log12
Answers
Answer:
log 12 = 1.0761
Step-by-step explanation:
log 12
=log(3*2*2)
= log 3 +log 2+ log 2
=0.4771+0.3010+0.3010
=1.0761
Answer:
Log 12 = 1.0791
Step-by-step explanation:
=> log (12)
Prime Factorizing 12
=> log (2×2×3)
Using log rule : \(log (a*b) = log a+logb\)
=> Log 2 + log 2 + log 3
Given that log 2 = 0.3010 , log 3 = 0.4771
=> 0.3010 + 0.3010 + 0.4771
=> 1.0791
Determine whether each pair of expressions is equivalent.
Select antor Not Equivalen for each pair of expressions.
3/4p + 2) and 12p + 6
O Equivalent
O Not Equivalent
O Equivalent
Not Equivalent
rand 2
29+ zdaniy y+2+2
O Equivalent
Not Equivalent
156 +5 and 5 (3+1)
Equivalent
O Not Equivalent

Answers
Step-By-Step Solution for Part 1:
3(4p + 2) = 12p + 6=> (3 x 4p) + (3 x 2) = 12p + 6=> 12p + 6 = 12p + 6Answer: Equivalent
________________________________________________Step-By-Step Solution for Part 2:
r + r = 2r=> 2r = 2rAnswer: Equivalent
________________________________________________Step-By-Step Solution for Part 3:
2y + z² = y x y + z + z=> 2y + z² = y² + 2z[Replacing y as 2 and z as 3]
=> 2(2) + (3)² = (2)² + 2(3)=> 4 + 9 = 4 + 6=> 13 ≠ 10Answer: Not Equivalent
________________________________________________Step-By-Step Solution for Part 4:
15n + 5 = 5(3n + 1)
=> 15n + 5 = (5 x 3n) + (5 x 1)
=> 15n + 5 = 15n + 5
Answer: Equivalent
________________________________________________Please help I forgot how to compare fractions
Is 17/20 bigger than 7/9
please help hurry
Answers
Answer:
Yes 17/20 is bigger than 7/9
Step-by-step explanation:
17 divided by 20 = 0.85
7 divided by 9 = 0.778 ish
17/20 is bigger
Step by step explaination. please and thank you

Answers
The interest to be paid on $120 at 5% rate for 6 years is $36
What is the rate of a simple interestSimple interest is the amount paid on a principal amount of money that is borrowed or loaned to someone. It is calculated using the formula: SI = (P × R × T) / 100. Where P is the principal amount, R is the rate and T is the time.
From the question;
P = $120
R = 5%
T = 6years
we shall evaluate for the simple interest as follows:
Simple interest = ($120 × 5 × 6)/ 100
Simple interest = $3600/100
Simple interest = $36
Therefore, the interest to be paid on $120 at 5% rate for 6 years is $36.
Read more about simple interest here:https://brainly.com/question/25793394
#SPJ1
A ball is released at the left end of three different tracks. The tracks are bent from equal-length pieces of channel iron.
a. From fastest to slowest, rank the speeds of the balls at the right ends of the tracks.
b. From longest to shortest, rank the tracks in terms of the times for the balls to reach the ends.
c. From greatest to least, rank the tracks in terms of the average speeds of the balls. Or do all the balls have the same average speed on all three tracks?
Answers
a. From fastest to slowest, the speeds of the balls at the right ends of the tracks will depend on the curvature of the tracks.
If the tracks are of equal length but have different curvatures, the ball on the track with the least curvature will have the highest speed, followed by the ball on the track with the next least curvature, followed by the ball on the track with the most curvature.
b. From longest to shortest, the tracks in terms of the times for the balls to reach the ends will depend on the curvature of the tracks. If the tracks are of equal length but have different curvatures, the track with the most curvature will have the longest time for the ball to reach the end, followed by the track with the next most curvature, followed by the track with the least curvature.
c. From greatest to least, the tracks in terms of the average speeds of the balls will depend on the curvature of the tracks. If the tracks are of equal length but have different curvatures, the track with the least curvature will have the highest average speed, followed by the track with the next least curvature, followed by the track with the most curvature.
All the balls will have the same average speed on all three tracks if the track lengths are equal, but will have different speeds at the end of each track due to the different curvatures.
know more about speeds here
https://brainly.com/question/28224010#
#SPJ11
Parameterize the line through p=(3,−5) and q=(8,0) so that the points p and q correspond to the parameter values t=9 and 12.
Answers
The parameterization of the line through points p=(3,-5) and q=(8,0) where p corresponds to t=9 and q corresponds to t=12 is given by the equations x = t - 6 and y = t - 14.
To parameterize the line, we need to find equations that express x and y in terms of a parameter t. We can start by determining the slope of the line using the coordinates of points p and q:
slope (m) = (y₂ - y₁) / (x₂ - x₁)
= (0 - (-5)) / (8 - 3)
= 5 / 5
= 1
Now that we have the slope, we can write the equations in point-slope form using point p:
y - y₁ = m(x - x₁)
y - (-5) = 1(x - 3)
y + 5 = x - 3
y = x - 8
Next, we can express x and y in terms of the parameter t by substituting x = 3 + (t - 9) and y = -5 + (t - 9) into the equation above. Simplifying, we get:
y = (3 + (t - 9)) - 8
y = t - 9 - 5
y = t - 14
Therefore, the parameterization of the line through points p and q where p corresponds to t=9 and q corresponds to t=12 is given by the equations x = 3 + (t - 9) and y = -5 + (t - 9), or equivalently, x = t - 6 and y = t - 14.
Learn more about parameterization here:
https://brainly.com/question/31964038
#SPJ11
Given that x= –1/2 and y = 4 , evaluate 3x²y + xy²
Answers
Answer:
-5
Step-by-step explanation:
3x²y + xy²
Let x = -1/2 and y = 4
3(-1/2)^2 (4) + (-1/2) (4)^2
Exponents first
3(1/4) (4) + (-1/2) 16
Multiply
3 - 8
Subtract
-5
Answer: \(\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\la\la\la\la\ddddddddddddddddddddddddddddddddcleverdddddd\ffffffffffffffffffffffffffffffffffffffff\pppppppppppppppppppppppppppppppppppp\ddddddddddddddddddd\huge \boldsymbol {-5}\)
Step-by-step explanation: simplify it \(\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\la\la\la\la\ddddddddddddddddddddddddddddddddcleverdddddd\ffffffffffffffffffffffffffffffffffffffff\pppppppppppppppppppppppppppppppppppp\ddddddddddddddddddd \displaystyle\ \Large \boldsymbol{} 3x^2y+xy^2=xy(3x+y)\) evalute \(\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\la\la\la\la\ddddddddddddddddddddddddddddddddcleverdddddd\ffffffffffffffffffffffffffffffffffffffff\pppppppppppppppppppppppppppppppppppp\ddddddddddddddddddd \displaystyle\ \Large \boldsymbol{} -\frac{1}{2} \cdot 4 (-3\cdot \frac{1}{2}+4)=-2\!\!\!\!\diagup\cdot\frac{5}{2\!\!\!\!\diagup} =\boxed{-5}\)
suppose the probability that maya is home is 1/3 and the probability that jim is home is 1/4. but the probability that jim is home given that maya is home is 1/2. what's the probability that they're both home?
Answers
The probability that they're both home is 1/12.
In the given question,
Probability of Maya at home P(A) = 1/3
And probability of Jim at home P(B) = 1/4
The probability that Jim is home given that maya is home P(A∪B) = 1/2
We have to find the probability when they both are at home P(A ∩ B).
As we can see that the probability of both the events are independent
So, we can use
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Therefore,
1/2 = 1/3 +1/4 – P(A ∩ B)
P(A ∩ B) = 7/12 – 1/2
P(A ∩ B) = 1/12
Hence, the probability that they're both home is 1/12.
To learn more about probability link is here.
brainly.com/question/11234923
#SPJ4
If m∠2 = 120°, what is m∠7?

Answers
if angle m∠2 = 120°, then m∠7 is 120°.
What are Angles?An angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
Supplementary angles are those angles that sum up to 180 degrees.
Given that m∠2 = 120°.
We have to find the m∠7.
m∠2 and m∠4 are supplementary angles.
120+m∠4=180
m∠4=60 degrees.
m∠4 is corresponding angle of m∠8.
m∠8 and m∠7 are again supplementary angles.
60+m∠7=180
m∠7=120 degrees.
Hence, if angle m∠2 = 120°, then m∠7 is 120°.
To learn more on Angles click:
brainly.com/question/28451077
#SPJ1
A student wrote the arithmetic series 8 + 11 + ... + 29 in summation notation as (picture below)
a. Describe and correct the error in the notation.
b. Evaluate the corrected summation of arithmetic series above.
\(S_8=\)
c. Write the explicit and recursive *formulas* for the arithmetic series above.
Explicit:
\(a_n=\)
Recursive:
If \(a_1=\)
Then for n > 1
\(a_n=\)
Answers
Therefore, for n > 1, we have: arithmetic series: a(n) = a(n-1) + 3
arithmetic series?
a. The correct notation for the arithmetic series 8 + 11 + ... + 29 would be:
∑(n=1 to 11) (7 + 3n)
The student's error is not specifying the upper limit of the summation, which should be 11 because there are 11 terms in the series.
b. To evaluate the corrected summation notation, we can use the formula for the sum of an arithmetic series:
Sn = n/2(a1 + an)
where Sn is the sum of the first n terms, a1 is the first term, and an is the nth term.
In this case, a1 = 8 and an = 29, so we have:
\(Sn = n/2(8 + 29)\\Sn = n/2(37)\)
Substituting n = 11 (the number of terms), we get:
\(S11 = 11/2(37)\\S11 = 203.5\)
Therefore, the sum of the arithmetic series 8 + 11 + ... + 29 is 203.5.
c. The explicit formula for an arithmetic series is:
\(an = a1 + (n-1)d\)
where an is the nth term, a1 is the first term, and d is the common difference between consecutive terms.
In this case, a1 = 8 and d = 3, so we have:
\(an = 8 + (n-1)3\\an = 3n + 5\)
The recursive formula for an arithmetic series is:
\(a(n+1) = a(n) + d\)
where a(n+1) is the next term and a(n) is the current term.
In this case, the first term is a1 = 8, and the common difference is d = 3, so we have:
\(a(n+1) = a(n) + 3\\a(1) = 8\)
To learn more about common difference:
https://brainly.com/question/28584885
#SPJ1
265) Calculator exercise. Add the three vectors (all angles are in degrees): (5 angle(50))+(x=6, y= 8)+(4 angle(40) )=(8 angle(h)) (x=m,y=n). Determine g, h,m, and n. ans:4 =
Answers
The values of g, h, m, and n are as follows: g = 5,h = 90, m = 2, n = 8
To add vectors in the form of magnitude and angle, we need to separate the magnitudes and angles of the vectors. Let's break down the given vectors:
Vector 1: 5 angle(50)
Magnitude: 5
Angle: 50 degrees
Vector 2: (x=6, y=8)
Magnitude: sqrt(6^2 + 8^2) = 10
Angle: arctan(8/6) = arctan(4/3) ≈ 53.13 degrees
Vector 3: 4 angle(40)
Magnitude: 4
Angle: 40 degrees
Now, let's add the vectors component-wise:
Sum of x-components: 5cos(50) + 6 + 4cos(40) = 50.6428 + 6 + 40.766 = 3.214 + 6 + 3.064 = 12.278
Sum of y-components: 5sin(50) + 8 + 4sin(40) = 50.766 + 8 + 40.6428 = 3.83 + 8 + 2.5712 = 14.4012
To find the magnitude and angle of the resulting vector, we use the formulas:
Magnitude: sqrt((Sum of x-components)^2 + (Sum of y-components)^2)
Angle: arctan((Sum of y-components)/(Sum of x-components))
Magnitude of the resulting vector: sqrt(12.278^2 + 14.4012^2) ≈ 19.0195
Angle of the resulting vector: arctan(14.4012/12.278) ≈ 48.60 degrees
Comparing the magnitude and angle with the given value:
Magnitude: 19.0195 ≈ 8 (g = 5)
Angle: 48.60 ≈ 90 (h = 90)
Therefore, the values of g, h, m, and n are as follows:
g = 5
h = 90
m = 2
n = 8
Note: The values of m and n are not directly related to the vectors provided in the question, so they are assigned arbitrary values for this exercise.
Learn more about vector addition here: brainly.com/question/28875206
#SPJ11
Math school please need help

Answers
Answer:
r² = (9 - 4)² + (6 - 4)² = 5² + 2² = 25 + 4 = 29
So the equation of this circle is
(x - 4)² + (y - 4)² = 29
Which word signals a sequence text structure?
both
finally
similarly
since
Answers
Answer:
its finally sorry it tooke so long
Step-by-step explanation:
Answer:
The answer is finally.
Step-by-step explanation: Both would be a compare and contrast text structure and so would similarly. Since would be a cause and effect text structure so the answer has to be finally. You can also tell because it is using key clues like then, after, and finally.
carmine drops a ball at shoulder height from the top of a building (as seen at the left). if the ball is at rest, and is simply dropped, how long will it take, to the nearest tenth of a second, to hit the ground?
Answers
The ball will take around 1.6 seconds to hit the ground when dropped from shoulder height at the top of the 35-foot tall building, considering a gravitational acceleration of 32.2 feet per second squared.
To find the time it takes for the ball to hit the ground, we can use the equations of motion under constant acceleration. The acceleration due to gravity near the surface of the Earth is approximately 32.2 feet per second squared.
First, let's calculate the total distance the ball needs to travel from the top of the building to the ground. The total height is the height of the building plus Carmine's height, which is 35 feet + 5 feet = 40 feet.
Next, we can use the equation:
\(s = ut + (1/2)at^2\)
where:
s = distance (40 feet)
u = initial velocity (0 feet per second since the ball is at rest)
a = acceleration (-32.2 feet per second squared, taking negative because the ball is moving downward)
t = time (unknown)
Plugging in the values:
\(40 = 0t + (1/2)(-32.2)t^2\)
Simplifying the equation:
\(40 = -16.1t^2\)
Dividing both sides by -16.1:
\(t^2 = -2.48\)
Since time cannot be negative in this context, we discard the negative solution. Taking the square root of the positive solution:
t ≈ 1.57 seconds
Therefore, it will take approximately 1.6 seconds (rounded to the nearest tenth) for the ball to hit the ground when dropped from shoulder height at the top of the building.
Learn more about height here: https://brainly.com/question/29131380
#SPJ11
The complete question is:
Carmine drops a ball at shoulder height from the top of a building (building is 35 feet tall, Carmine is 5 feet tall). If the ball is at rest, and is simply dropped, how long will it take, to the nearest tenth of a second, to hit the ground?
a polyhedron has all faces triangles or quadrilaterals, and $1001$ edges. what is the difference between the maximum and minimum possible numbers of faces?
Answers
Using Euler'formula, the difference between maximum and minimum possible numbers of faces is 96.
A polyhedron is a 3D shape with flat faces, straight edges, and sharp vertices (corners). "polyhedron" meaning "many" and "polyhedron" meaning "area". Therefore, when many planes are joined, they form a polyhedron.
Because all faces are triangles. So on a triangular base with triangular faces on both sides that meet at the vertex.
Therefore, the minimum number of triangular faces of a regular polyhedron is = 4
Next, the double pyramid has "2n" triangular faces. where n is a natural number greater than 2 and 'n' represents the number of sides of the base of the pyramid.
A polyhedron having equal quadrilateral faces is known as regular hexahedron.
quadrilateral faced polyhedron with total sides 100 and vertices 6 , then using Euler's formula
F + V-E = 2
=> F + 6- 100= 2 => F = 96 maximum faces possible = 96
Now the difference between maximum and minimum number of faces = 100 - 4 = 96
So the difference between maximum and minimum faces is 96.
To learn more about Polyhedron, refer:
https://brainly.com/question/27231951
#SPJ4
Consider the general problem: -(ku')' + cu' + bu = f, 0 Suppose we discretize by the finite element method with 4 elements. On the first and last elements, use linear shape functions, and on the middle two elements, use quadratic shape functions. Sketch the resulting basis functions. What is the structure of the stiffness matrix K (ignoring boundary conditions); that is indicate which entries in K are nonzero.
Answers
We need to consider the general problem: \[-(ku')' + cu' + bu = f\]If we discretize by the finite element method with four elements.
On the first and last elements, we use linear shape functions, and on the middle two elements, we use quadratic shape functions. The resulting basis functions are given by:The basis functions ϕ1 and ϕ4 are linear while ϕ2 and ϕ3 are quadratic in nature. These basis functions are such that they follow the property of linearity and quadratic nature on each of the elements.
For the structure of the stiffness matrix K, we need to consider the discrete problem given by \[KU=F\]where U is the vector of nodal values of u, K is the stiffness matrix and F is the load vector. Considering the above equation and assuming constant values of k and c on each of the element we can write\[k_{1}\begin{bmatrix}1 & -1\\-1 & 1\end{bmatrix}+k_{2}\begin{bmatrix}2 & -2 & 1\\-2 & 4 & -2\\1 & -2 & 2\end{bmatrix}+k_{3}\begin{bmatrix}2 & -1\\-1 & 1\end{bmatrix}\]Here, the subscripts denote the element number. As we can observe, the resulting stiffness matrix K is symmetric and has a banded structure.
The element [1 1] and [2 2] are common to two elements while all the other elements are present on a single element only. Hence, we have four elements with five degrees of freedom. Thus, the stiffness matrix will be a 5 x 5 matrix and the structure of K is as follows:
$$\begin{bmatrix}k_{1}+2k_{2}& -k_{2}& & &\\-k_{2}&k_{2}+2k_{3} & -k_{3} & & \\ & -k_{3} & k_{1}+2k_{2}&-k_{2}& \\ & &-k_{2}& k_{2}+2k_{3}&-k_{3}\\ & & & -k_{3} & k_{3}+k_{2}\end{bmatrix}$$Conclusion:In this question, we considered the general problem given by -(ku')' + cu' + bu = f. We discretized it by the finite element method with four elements. On the first and last elements, we used linear shape functions, and on the middle two elements, we used quadratic shape functions. We sketched the resulting basis functions. The structure of the stiffness matrix K was then determined by ignoring boundary conditions. We observed that it is symmetric and has a banded structure.
To know more about general problem visit
https://brainly.com/question/24486535
#SPJ11
PLEASEEE HELPPPPP :(((
Solve for x.
5(x−2 2/5)=−5.2
Enter your answer as a decimal in the box.
Answers
if r(x) = 3x – 1 and s(x) = 2x + 1, which expression is equivalent to ?
a. 3 (6)-1/2(6) +1
b. (6)/ 2(6)+1
c. 36-1/26+1
d. (6)-1/(6)+1
Answers
If the expression \(r(x) = 3x - 1\) and the expression \(s(x) = 2x + 1\) , then the expression equivalent to \(\frac{r}{s} (6)\) is (a) \(\frac{3(6)-1}{2(6) +1}\) .
What are Algebraic Expression ?
The algebraic Expression are defined as the expressions that are written with the combination of variables and constants joined by mathematical operators , For Example : \(3x+7\) .
Here the two expressions are given as \(r(x) = 3x - 1\) and \(s(x) = 2x + 1\) ;
we have to find equivalent expression for \(\frac{r}{s} (6)\) ;
By the Division Property of Algebraic Expression ;
it can be written as : \(\frac{r(6)}{s(6)}\) ;
So , Substituting \(x=6\) , in r(x) ,
we get ; \(r(6) = 3(6) - 1\) , ......equation(1)
On Substituting \(x=6\) , in s(x) ,
we get ; \(s(6) = 2(6)+1\) , ....equation(2) ;
Substituting the values of r(6) and s(6) from equation(1) and equation(2) in \(\frac{r(6)}{s(6)}\) ;
we get ;
⇒ \(\frac{r(6)}{s(6)} = \frac{3(6)-1}{2(6) +1}\) ;
Therefore , the expression equivalent to \(\frac{r}{s} (6)\) is \(\frac{3(6)-1}{2(6) +1}\) .
The given question is incomplete , the complete question is
If r(x) = 3x - 1 and s(x) = 2x + 1, which expression is equivalent to r/s(6) ?
(a) \(\frac{3(6)-1}{2(6) +1}\)
(b) \(\frac{(6)}{2(6)+1}\)
(c) \(\frac{36-1}{26+1}\)
(d) \(\frac{(6)-1}{(6)+1}\)
Learn more about Expression here
https://brainly.com/question/12011094
#SPJ4
On a map, the scale shown is 1 inch : 5 miles. If a park is 75 square miles, what is the area of the park on the map?
Answers
Given:
On a map, the scale shown is 1 inch : 5 miles.
Area of park = 75 square miles.
To find:
The area of the park on the map.
Solution:
Ratio of the areas of similar figures is equal to the ratio square of their corresponding sides.
\(\dfrac{\text{Area of park on the map}}{\text{Actual area of the park}}=\dfrac{\text{Side of park in map}^2}{\text{Actual side of park}^2}\)
Let A be the area of the park on the map.
\(\dfrac{A}{75}=\dfrac{1^2}{5^2}\)
\(A=\dfrac{1}{25}\times 75\)
\(A=3\)
Therefore, the area of the park on the map is 3 square inches.