The amount of time spent by North Americanadults watching television per day is normally distributedwith a mean of 6 hours and a standarddeviation of 1.5 hours.a. What is the probability that a randomly selectedNorth American adult watches television formore than 7 hours per day?b. What is the probability that the average timewatching television by a random sample of fiveNorth American adults is more than 7 hours?c. What is the probability that in a random sampleof five North American adults, all watch televisionfor more than 7 hours per day?
Answers
The probability that in a random sample of five North American adults, all watch television for more than 7 hours per day is 0.000793 or approximately 0.08%.
a. To find the probability that a randomly selected North American adult watches television for more than 7 hours per day, we need to calculate the z-score and then use a standard normal distribution table or calculator.
z-score = (7 - 6) / 1.5 = 0.67
Using a standard normal distribution table or calculator, we find that the probability of a z-score greater than 0.67 is 0.2514. Therefore, the probability that a randomly selected North American adult watches television for more than 7 hours per day is 0.2514.
b. The distribution of the sample mean is also normal with mean = 6 and standard deviation = 1.5 / sqrt(5) = 0.67.
z-score = (7 - 6) / (1.5 / sqrt(5)) = 1.34
Using a standard normal distribution table or calculator, we find that the probability of a z-score greater than 1.34 is 0.0885. Therefore, the probability that the average time watching television by a random sample of five North American adults is more than 7 hours is 0.0885.
c. The probability that a single North American adult watches television for more than 7 hours is 0.2514 (from part a). The probability that all five adults in the sample watch television for more than 7 hours can be calculated using the binomial distribution:
P(X = 5) = (5 choose 5) * 0.2514^5 * (1 - 0.2514)^(5-5) = 0.000793
Therefore, the probability that in a random sample of five North American adults, all watch television for more than 7 hours per day is 0.000793 or approximately 0.08%.
To learn more about probability visit: https://brainly.com/question/30034780
#SPJ11
Related Questions
ILL GIVE U BRAINLESSTT!!!

Answers
which number has an absolute value that is greater then 50?
Answers
For the function below find a) the critical numbers; b) the open intervals where the function is increasing, and c) the open intervals where it is decreasing f(x)=8x³-42x-48x + 4 a) Find the critical number(s). Select the correct choice below and, if necessary fill in the answer box to complete your choice. A. The critical number(s) is/are (Type an integer or a simplified fraction. Use a comma to separate answers as needed
Answers
A) Function is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).
b) The local minimum value of f is; 5608/2197 at x = -42/13, and the local maximum value of f is 139/8 at x = 7/2.
(a) To determine the intervals on which f is increasing or decreasing, we need to determine the critical points and then check the sign of the derivative on the intervals between them.
f(x)=8x³-42x-48x + 4
f'(x) = 24x² - 90
Setting f'(x) = 0, we get
24x² - 90 = 0
24x² = 90
x =± √3.75
So, the critical points are;
x = -1 and x = 7/2.
We can test the sign of f'(x) on the intervals as; (-∞, -1), (-1, 7/2), and (7/2, ∞).
f'(-2) = 72 > 0, so f is increasing on (-∞, -1).
f'(-1/2) = -25 < 0, so f is decreasing on (-1, 7/2).
f'(4) = 72 > 0, so f is increasing on (7/2, ∞).
Therefore, f is increasing on (-∞, -1) and (7/2, ∞), and decreasing on (-1, 7/2).
(b) To determine the local maximum and minimum values of f, we need to look at the critical points and the endpoints of the interval (-1, 7/2).
f(-1) = -49
f(7/2) = 139/8
f(-42/13) = 5608/2197
Learn more about maximum value here:
brainly.com/question/23504923
#SPJ4
which quadratic equations are in standard form. 1-7x^2=-x. 1/2x^2+4x-3=0. x^5-3x+9=0. 0.5x^2-3.2x+5.8=0. (x+5)^2-3=0. -x^2-3x+20=0.
Answers
The equations that are in standard form are B) \(1/2x^2 + 4x - 3 = 0\) and E) -\(x^2 - 3x + 20 = 0\). Option B and E.
Quadratic equations in standard form have the general form of "ax^2 + bx + c = 0", where a, b, and c are constants. Let's analyze each equation to determine if it is in standard form:
A)\(1 - 7x^2 = -x\)
This equation is not in standard form because the term with the highest power, 7x^2, has a negative coefficient. To put it in standard form, we can rearrange the equation: \(7x^2 - x - 1 = 0.\)
B) \(1/2x^2 + 4x - 3 = 0\)
This equation is in standard form. The coefficients of x^2, x, and the constant term are all numerical values.
C) \(x^5 - 3x + 9 = 0\)
This equation is not a quadratic equation since it has a term with the power of 5. Quadratic equations only involve terms with the power of 2. Therefore, this equation is not in standard form.
D)\((x + 5)^2 - 3 = 0\)
This equation is not in standard form. To put it in standard form, we can expand the square:\(x^2 + 10x + 25 - 3 = 0\). Simplifying further, we get \(x^2 + 10x + 22 = 0.\)
E) \(-x^2 - 3x + 20 = 0\)
This equation is in standard form. The coefficients of \(x^2\), x, and the constant term are all numerical values.
For more such questions on equations visit:
https://brainly.com/question/17145398
#SPJ8
Besides being simple for its own sake, what other advantage do simple models usually have?
a) Higher accuracy
b) Greater complexity
c) Easier interpretation
d) More detailed predictions
Answers
The correct option is c) Easier interpretation. One of the main advantages of simple models is their ease of interpretation. Simple models tend to have fewer parameters and less complex mathematical equations, making it easier to understand and interpret how the model is making predictions.
This interpretability can be valuable in various domains, such as medicine, finance, or legal systems, where it is important to have transparent and understandable decision-making processes.
Complex models, on the other hand, often involve intricate relationships and numerous parameters, which can make it challenging to comprehend the underlying reasoning behind their predictions. While complex models can sometimes offer higher accuracy or make more detailed predictions, they often sacrifice interpretability in the process.
To know more about complex visit-
brainly.com/question/28235673
#SPJ11
Use the information shown in the line plot.
How many fruit baskets weigh more than
4
1
2
412
pounds and less than
6
pounds?
Enter your answer in the box.
_____fruit baskets
Answers
Answer:
8.
Step-by-step explanation:
5 and 5 1/2 are the only fractions between 4 and 6. There are 4 dots above each, and 4 x 2 = 8. (I know the amount of dots because I had this question.)
There are two baskets that weigh more than 4 but less than 6.
The weights of fruit baskets are:
4, 1, 2, 5, 5(1/2), 6
What is weight?Weight is the quantity of matter in a physical body.
We can see that fruit baskets that weigh more than 4 pounds but less than 6 pounds are ones with weights of 5 pounds and 5(1/2) pounds.
So, there are two baskets that weigh more than 4 but less than 6.
Thus, there are two baskets that weigh more than 4 but less than 6.
To get more about weight visit:
https://brainly.com/question/2337612
I NEED HELP ON THIS ONE TOO SAME THING ILL GIVE BRAINLIEST
Cassidy plans to paint the four walls of her bedroom. Each wall measures 12 feet by 10 feet. The window measures 2.5 feet by 4 feet. The door measures 3 feet by 7 feet. How many square feet will Cassidy paint if she does not paint the window and door? Sketch the figure below and show are calculations.
Answers
Answer:
449 sq ft
Step-by-step explanation:
which equation doesn't represent the multiplicative identity property?
A. 444*1=444
B. 293*1=293
C. 222*1=222
D. 675*0=0
Answers
Answer:
d
Step-by-step explanation:
Answer:
None of them
Step-by-step explanation:
It clearly shows all multiplication operation. On top of that, they are all correct and accurate answers as well. Maybe there is a typo, but as what I can see there is no other operation used in any of the equations.
what is equal to 16x103
Answers
Answer:
1648
Step-by-step explanation:
Let's use the distributive property:
(16 x 100) + (10 x 3) + (6 x 3) =
1600 + 30 + 18 = 1648
-Chetan K
as a part of a customer loyalty program, a restaurant's computer chooses orders at random to receive a free appetizer. each order has a 111 in 181818 chance of receiving a free appetizer. (each order is limited to one free appetizer.) let xxx be the number of orders the restaurant fills in a day until they give away the first appetizer. assume that each order getting the appetizer is independent. find the probability that the restaurant first gives away an appetizer on the 6^{\text{th}}6 th 6, start superscript, start text, t, h, end text, end superscript order of the day.
Answers
The probability of the 6th order being the order with the free appetizer is 0.0417 (approx).
The probability of an event occurring is defined by probability. There are many instances in real life where we may need to make predictions about how something will turn out. The outcome of an event may be known to us or unknown to us. When this happens, we say that there is a chance that the event will happen or not. In general, probability has many wonderful uses in games, in business to make forecasts based on likelihood, and in this emerging branch of artificial intelligence.
The probability of getting a free appetizer is 1/18.
The probability of not getting a free appetizer is 17/18.
If the restaurant gives away an appetizer on the 6th order, then there must have been 5 orders before the 6th one that had no free appetizer, followed by the one with the free appetizer.
\(P (X = 6) = P(N N N N N F)\)
= 17/18 x 17/18 x 17/18 x 17/18 x 17/18 x 1/18
\(= \frac{17^4}{18^5}\) ≈ 0.0417
Thus, the probability of the 6th order being the order with the free appetizer is 0.0417 (approx).
To learn more about probability, visit the link:
brainly.com/question/30034780
#SPJ4
The volume of the moon is about 2.18x10^10 cubic kilometers. The volume of Earth is about 1.09x10^13 cubic kilometers. The number of moons that can fit inside Earth can be found by dividing Earth’s volume by the moon volume. About how many moons can fit inside earth
Answers
Answer:
Step-by-step explanation:
provide numerical measures of individuals. the measures can be added or subtracted, and provide a results.
Answers
Numerical measures of individuals can be calculated by adding or subtracting values that represent a person’s attributes.
For example, a person’s IQ score is calculated by subtracting their mental age from their chronological age, then multiplying the difference by 100. The IQ score formula is IQ = (MA/CA) x 100, where MA is the mental age and CA is the chronological age. So, for example, if a person is 20 years old but has a mental age of 15, their IQ score would be 75 ((15/20) x 100). This numerical measure is useful for determining an individual’s cognitive abilities. Other numerical measures of individuals include body mass index (BMI), which is calculated by dividing a person’s weight in kilograms by their height in meters squared. BMI = Weight (kg) ÷ [Height (m)]2. For example, a person who weighs 70 kg and is 1.7 m tall would have a BMI of 24.2 (70 ÷ [1.7]2). BMI is used to determine whether or not an individual is overweight or obese.
Learn more about Numerical measures here:
https://brainly.com/question/29628072
#SPJ4
\(x = 8\)I need help solving this.
Answers
Answer:
2
Step-by-step explanation:
x³ = 8
∛8 = 2
found by 2 • 2 • 2 = 4 • 2 = 8
what is the expected value (Lesson 8.3: Unbiased Point Estimation. If X1, of the sample variance S2? a. 1/6 b. 1/36 O c. 6 d. 36 e.60
Answers
The correct answer is option b. 1/36 is the expected value (Lesson 8.3: Unbiased Point Estimation. If X1, of the sample variance S2.
In unbiased point estimation, the expected value of the sample variance S2 is a crucial idea. When a sample is drawn from a population repeatedly, an average value of S2 is what is anticipated.
The population variance divided by the sample size represents the expected value of S2. It is, in other words, the population variance divided by n-1, where n is the sample size.
As a result, the expected value of the sample variance S2 for a sample size of 6 is equal to 1/36.
As a result, when a sample is drawn from a population repeatedly, the average value of S2 will be equal to 1/36 of the variance in the population.
Complete Question:
What is the expected value (Lesson 8.3: Unbiased Point Estimation. If X1, of the sample variance S2?
a. 1/6
b. 1/36
c. 6
d. 36
e.60
To learn more about unbiased visit:
https://brainly.com/question/22777338
#SPJ4
what is the area of this figure

Answers
Answer:
174.5m
Step-by-step explanation:
So we have to break the shapes down to triangle, rectangle and the small rectangle
Area of rectangle=WxL
Area of triangle= (BxH)÷2
triangle=
(23x11)÷2
=253÷2
=126.5m
rectangle=
9x19
=28m
square#2(the small one)=
5x4
=20m
All:
20+28+126.5
=174.5m
Subtract (4+2i) from (6-8i). Enter your answer as a complex number in the
form a+bi.
Answers
(4+2i) side note : -8i - 2i becomes 8i+2i 2+10i because the negatives cancel out
^^^answer
The point P(2k, k) is equidistant from A(-2, 4) and B (7,-5). Find the value of k.
Answers
If point P(2k, k) is equidistant from A(-2, 4) and B (7,-5), the numerical value of k is 3.
What is the numerical value of k?The distance formula used in finding the distance between two points is expressed as;
d = √( ( x₂ - x₁ )² + ( y₂ - y₁ )² )
The distance between P(2k, k) and A(-2, 4) is:
d = √((2k - (-2))² + (k - 4)²)
d = √((2k +2)² + (k - 4)²)
The distance between P(2k, k) and B(7, -5) is:
d = √((2k - 7)² + (k - (-5))²)
d = √((2k - 7)² + (k + 5)² )
Since the distances are equal, we can set the two equations for d equal to each other and solve for k.
√((2k +2)² + (k - 4)²) = √((2k - 7)² + (k + 5)² )
Square both sides
(2k +2)² + (k - 4)² = (2k - 7)² + (k + 5)²
(2k +2)² + (k - 4)² = 5k² - 18k + 74
5k² + 20 = 5k² - 18k + 74
Collect like terms
5k² - 5k² + 18k = 74 - 20
18k = 74 - 20
18k = 54
k = 54/18
k = 3
Therefore, the value of k is 3.
Learn more about the distance formula here: brainly.com/question/24509115
#SPJ1
Neha has a piece of ribbon of length 23 cm, correct to the nearest cm.
From this ribbon she cuts off a piece with length 87 mm, correct to the nearest mm.
Work out the lower bound and the upper bound for the length of the remaining ribbon.
Give your answer in centimetres.
Lower bound =
Upper bound =
Answers
The lower bound for the length of the remaining ribbon is 13.8 cm, and the upper bound is 15.8 cm.
Here,
To work out the lower and upper bounds for the length of the remaining ribbon, we need to consider the possible scenarios that would result in the smallest and largest remaining lengths.
Given:
Original length of ribbon = 23 cm (correct to the nearest cm)
Length of the piece cut off = 87 mm (correct to the nearest mm)
First, let's convert the length of the piece cut off to centimeters:
1 cm = 10 mm
So, 87 mm = 87 / 10 cm = 8.7 cm (correct to the nearest mm)
Now, let's calculate the upper bound for the remaining ribbon length:
Upper bound = Original length - Length cut off + Tolerance
Upper bound = 23 cm - 8.7 cm + 0.5 cm (maximum possible rounding error for 87 mm)
Upper bound = 23 cm - 8.7 cm + 0.5 cm = 15.8 cm
Next, let's calculate the lower bound for the remaining ribbon length:
Lower bound = Original length - Length cut off - Tolerance
Lower bound = 23 cm - 8.7 cm - 0.5 cm (maximum possible rounding error for 87 mm)
Lower bound = 23 cm - 8.7 cm - 0.5 cm = 13.8 cm
So, the lower bound for the length of the remaining ribbon is 13.8 cm, and the upper bound is 15.8 cm.
learn more on length :
https://brainly.com/question/32832640
#SPJ4
Find the slip and slide trinomials if 16k2 -24k + 8
Answers
In order to use the slip and slide method, first, we multiply the leading coefficient by the constant term, rewriting the expression will look like this:
\(\begin{gathered} k^2-24k+(8\times16) \\ k^2-24k+128 \end{gathered}\)factor the expression using two numbers that multiplied together are equal to 128 and added together are equal to -24,
\((k-8)(k-16)\)then, divide both terms by the 16 we multiplied first
\(\begin{gathered} (k-\frac{8}{16})(k-\frac{16}{16}) \\ (k-\frac{1}{2})(k-1) \end{gathered}\)rewrite the terms by sliding the denominator in front of the variable,
\((2k-1)(k-1)\)use simpson's rule with n=4 to approximate the solution to part b at x=0.5 to three decimal places.
Answers
Using the value of ∫01x3+1dx obtained above, we can approximate the value of∫0.50x3+1dx as:Simpson's Rule ∫abf(x)dx≈b−a3n[f(a)+2∑i=12n−1f(ai)+4∑i=14n−1f(xi)+f(b)]≈15[0+2{(13)3+1}+4{(14)3+1}+13+3]≈0.7828Therefore, the solution to part b at x=0.5 to three decimal places is approximately equal to 0.7828.
The solution to part b at x
=0.5 to three decimal places using Simpson's Rule with n
=4 is given as follows:Approximate the value of∫01x3+1dx, with Simpson's Rule using n
=4 subintervals.Simpson's Rule formula for integrating a function, f(x), with n subintervals is given as:Simpson's Rule ∫abf(x)dx≈b−a3n[f(a)+2∑i
=12n−1f(ai)+4∑i
=14n−1f(xi)+f(b)]where h
=(b−a)n and xi
=a+ih for i
=1,2,3,...,n.Substituting a
=0, b=1, f(x)
=x3+1, and n
=4 in Simpson's Rule formula:∫01x3+1dx≈14[0+2{(13)3+1+(23)3+1}+4{(14)3+1+(34)3+1}+13+3]≈1.1354The value of ∫01x3+1dx is approximately equal to 1.1354, using Simpson's Rule with n
=4 subintervals. We want to approximate the solution to part b at x
=0.5 to three decimal places. Using the value of ∫01x3+1dx obtained above, we can approximate the value of∫0.50x3+1dx as:Simpson's Rule ∫abf(x)dx≈b−a3n[f(a)+2∑i
=12n−1f(ai)+4∑i
=14n−1f(xi)+f(b)]≈15[0+2{(13)3+1}+4{(14)3+1}+13+3]≈0.7828Therefore, the solution to part b at x
=0.5 to three decimal places is approximately equal to 0.7828.
To know more about approximately visit:
https://brainly.com/question/31695967
#SPJ11
please help me out i don't want to keep wasting points. no fake answers or i. will report
Points A=(3,5) B = (-2,6) C=(0,16) are vertices of a triangle
1. Find the slope of each segment
2. is the triangle a right triangle explain your answer
Answers
Answer:
hi again
6
x
−
3
y
=
12
x
+
6
y
=
5
3
x
+
y
=
16
Step-by-step explanation:
From a table of integrals, we know that for ,≠0a,b≠0,
∫cos()=⋅cos()+sin()2+2+.∫eatcos(bt)dt=eat⋅acos(bt)+bsin(bt)a2+b2+C.
Use this antiderivative to compute the following improper integral:
∫[infinity]01cos(3)− = limT→[infinity]∫0[infinity]e1tcos(3t)e−stdt = limT→[infinity] if ≠1s≠1
or
∫[infinity]01cos(3)− = limT→[infinity]∫0[infinity]e1tcos(3t)e−stdt = limT→[infinity] if =1.s=1. help (formulas)
For which values of s do the limits above exist? In other words, what is the domain of the Laplace transform of 1cos(3)e1tcos(3t)?
help (inequalities)
Evaluate the existing limit to compute the Laplace transform of 1cos(3)e1tcos(3t) on the domain you determined in the previous part:
()=L{e^1t cos(3)}=
Answers
"From a table of integrals, we know that for \(\(a \neq 0\)\) and \(\(b \neq 0\):\)
\(\[\int \cos(at) \, dt = \frac{1}{a} \cdot \cos(at) + \frac{1}{b} \cdot \sin(bt) + C\]\)
and
\(\[\int e^a t \cos(bt) \, dt = \frac{e^{at}}{a} \cdot \cos(bt) + \frac{b}{a^2 + b^2} \cdot \sin(bt) + C\]\)
Use this antiderivative to compute the following improper integral:
\(\[\int_{-\infty}^{0} \cos(3t) \, dt = \lim_{{T \to \infty}} \int_{0}^{T} e^t \cos(3t) \, e^{-st} \, dt = \lim_{{T \to \infty}} \text{ if } s \neq 1, \, \text{ or } \lim_{{T \to \infty}} \text{ if } s = 1.\]\)
For which values of \(\(s\)\) do the limits above exist? In other words, what is the domain of the Laplace transform of \(\(\frac{1}{\cos(3)} \cdot e^t \cos(3t)\)\)?
Evaluate the existing limit to compute the Laplace transform of on the domain you determined in the previous part:
\(\[L\{e^t \cos(3t)\\).
To know more about antiderivative visit-
brainly.com/question/9700015
#SPJ11
Deborah bought 3 identical bindersand received $1.15 change from $10.00. Use algebra to find out how much each binder cost. Show your work.
Answers
Answer:
$2.95
Step-by-step explanation:
math
The cost of each binder is $2.95.
What is Division?Division is one of the operation in mathematics where number is divided into equal parts as that of a definite number.
Given that,
Deborah bought 3 identical binders.
He received $1.15 change from $10.00.
Cost for 3 binders = $10.00 - $1.15
= $8.85
Since the 3 binders are identical, each costs the same.
Cost of each binder = $8.85 / 3
= $2.95
Hence the cost of each binder is $2.95.
To learn more about Division, click on the link :
https://brainly.com/question/13393738
#SPJ3
how many times does 226.08 go into 2034.72** URGENT**
Answers
Answer: 226.08 goes into 2034.72 9 times.
Step-by-step explanation: I hope this helped you!!!!! Have a great day. And stay safe!!!
5. Which expression is equivalent to
(3x^2y-4)^0?
Answers
Answer:
1
Step-by-step explanation:
It is 1 because the laws of exponents state that anything raised to the power of 0 is 1.
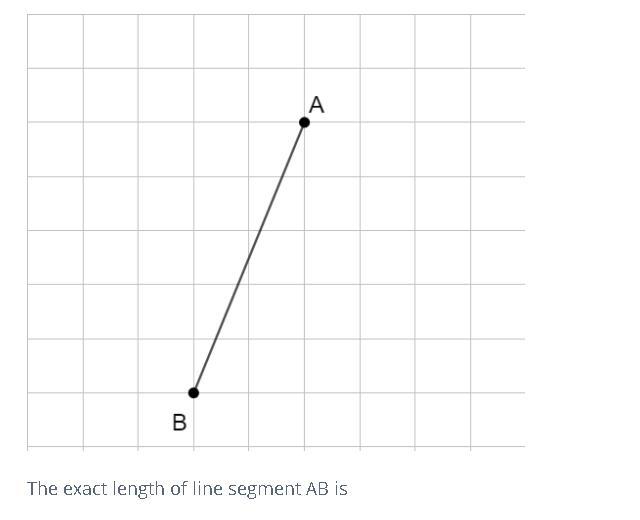
The exact length of line segment AB is?
Answers
Answer:
6in
Step-by-step explanation:
7) What does a multiplier of \( 1.2 \) mean?
Answers
A multiplier of 1.2 means the value is multiplied or increased by a factor of 1.2.
A multiplier is a term used to represent a factor by which a value is multiplied or increased. It is a numeric value that indicates the extent of the increase or expansion of a given quantity. Multiplication by a multiplier results in scaling or changing the magnitude of the original value.
A multiplier of 1.2 indicates that a value will be increased by 20% or multiplied by a factor of 1.2. This means that when the multiplier is applied to the original value, the resulting value will be 1.2 times the original.
Read more about multipliers:
brainly.com/question/15883095
Suppose n balls are distributed randomly into n compartments.
What is the probability that m balls will fall into the first compartment? Assume all the n arrangements are equally like.
Answers
The probability that m balls is P(m balls in first compartment) = (nCm) * ((n-1)^(n-m)) / (n^n).
The total number of possible arrangements of distributing n balls into n compartments is given by n^n. Each ball has n choices for which compartment to fall into, and since there are n balls, we multiply n by itself n times.
Now, let's consider the number of ways m balls can fall into the first compartment. We can choose m balls out of the n balls to go into the first compartment in nCm ways, which is the binomial coefficient.
The remaining (n-m) balls can go into any of the remaining (n-1) compartments in (n-1)^(n-m) ways. Therefore, the probability that m balls will fall into the first compartment is given by:
P(m balls in first compartment) = (nCm) * ((n-1)^(n-m)) / (n^n)
This formula calculates the ratio of favorable outcomes (m balls in the first compartment) to the total number of possible outcomes (all possible arrangements of distributing n balls into n compartments).
To know more about probability refer here:
https://brainly.com/question/31828911
#SPJ11
6. Multiply: i) 3x (5x+8y)
ii) 4x (3x2 + 5x-7)
iii) (3x+4y) (2x-7y)
iv) (2-3a) (2a2-3a+7)
Answers
Answer:
Step-by-step explanation:
3x(5x+8y)=15x^2+24xy
4x(3x^2+5x-7)=12x^3+20x^2-28x
(3x+4y)(2x-7y)=6x^2+8xy-21xy-28y^2=6x^2-13xy-28y^2
(2-3a)(2a^2-3a+7)=4a^2-6a+14-6a^3+9a^2-21a=-6a^3+13a^2-27a+14
help me pleaseeeeeeee

Answers
Answer:
x = -4/3 or x = 3/2
Step-by-step explanation:
Let's solve your equation step-by-step.
6x^2−x−12=0
Step 1: Factor left side of equation.
(3x+4)(2x−3)=0
Step 2: Set factors equal to 0.
3x+4=0 or 2x−3=0
x = -4/3 or x = 3/2
Answer:
x = -4/3 or x = 3/2