The product of
2x and 3y
Answers
Answer:
6xy
Step-by-step explanation:
(2x) × (3y)
=(2×3) × (x×y)
=6×xy
=6xy
Related Questions
Find the 8th term of the arithmetic sequence 3x-13x−1, -2x+6−2x+6, -7x+13, ...−7x+13,...
Answers
Answer:
11x +98 just assume it to be an arithmetic progression
AC is the diameter of the circle. Angle AWB is 120 degrees. How big is arc BC?

Answers
60 degrees is the measure of arc BC from the figure
Circle geometryThe given diagram is a circle with several arc angles
arcAWB = 120 degrees
The line AC is a diameter
Since the sum of angles on a straight line is 180 degrees, hence:
arc AWB + arcBC = 180
arcBC = 180 - arc ZWX
arcBC = 180 - 120
arcBC = 60 degrees
Hence the measure of the arc BC from the diagram is 60 degrees
Learn more on circle geometry here: https://brainly.com/question/24375372
#SPJ1
A researcher selects a sample of 32 participants who are assigned to participate in a study with one group. What are the degrees of freedom for this test
Answers
the degrees of freedom for this test Women found this trait to be important, and this result was significant, t(15)=8.00, p<.05
What is degrees of freedom?Various amounts of data or information can be used to estimate statistical parameters. The degrees of freedom refers to the quantity of independent data points used to estimate a parameter. The number of independent scores that are utilized in an estimate of a parameter, minus the number of parameters used as intermediary stages in the estimation of the parameter itself, is generally considered to be the measure of the degree of freedom of the estimate. The degrees of freedom, for instance, are equal to the number of independent scores (N) minus the number of parameters calculated as intermediary steps, or N 1, if the variance is to be estimated from a random sample of N independent scores.
To learn more about degrees of freedom from the given link:
https://brainly.com/question/25781718
#SPJ4
In a recent election, 63% of all registered voters participated in voting. In a survey of 275 retired voters, 162 participated in voting. Which is higher, the population proportion who participated or the sample proportion from this survey?
Answers
The population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
To determine whether the population proportion who participated in voting or the sample proportion from the survey is higher, we need to compare the percentages.
The population proportion who participated in voting is given as 63% of all registered voters.
This means that out of every 100 registered voters, 63 participated in voting.
In the survey of retired voters, 162 out of 275 participants voted. To calculate the sample proportion, we divide the number of retired voters who participated (162) by the total number of retired voters in the sample (275) and multiply by 100 to get a percentage.
Sample proportion = (162 / 275) \(\times\) 100 ≈ 58.91%, .
Comparing the population proportion (63%) with the sample proportion (58.91%), we can see that the population proportion who participated in voting (63%) is higher than the sample proportion from this survey (58.91%).
Therefore, based on the given data, the population proportion who participated in voting is higher than the sample proportion from this survey.
It's important to note that the sample proportion is an estimate based on the surveyed retired voters and may not perfectly represent the entire population of registered voters.
For similar question on population proportion.
https://brainly.com/question/29516589
#SPJ8
Math Help please show work please due soon uwu :3

Answers
Answer:
For the first question since 1 mile equals 1.6 km we have to divide, 14.4/1.6=9
For the second question the formula is to divide by 9, if we do this our anser will be 5.
For the third question the answer is 100,000 cm^2, the reason this is, is because if 1m^2=10,000cm^2 , 1x10=10 and 10x10,000=100,000
Hope I helped tell me if i have to clarify anything :)
let r be the shaded region in the first quadrant enclosed by the graphs of y=e^-x^2
how do you find the area of the region R?
Answers
To find the area of the shaded region R enclosed by the graphs of y = e^(-x^2) in the first quadrant, you can use integration.
The integral represents the area under a curve between two x-values. In this case, we want the area in the first quadrant, so we need to integrate the function from x = 0 to some positive x-value.
The integral to find the area of R is given by:
A = ∫[0 to a] e^(-x^2) dx
Unfortunately, there is no elementary function to find the antiderivative of e^(-x^2) in terms of elementary functions. Therefore, the integral cannot be evaluated using simple algebraic methods.
However, the integral can be approximated using numerical methods or specialized techniques such as Gaussian quadrature or Monte Carlo methods. These methods can provide an approximation of the area of the shaded region R.
Alternatively, you can use software or graphing calculators that have built-in functions to find definite integrals to numerically approximate the area under the curve.
To learn more about integration : brainly.com/question/31744185
#SPJ11
A TV has an original price of $499. Find the new price of the TV after a 10% increase.
Answers
Answer:
$548.9
Step-by-step explanation:
$499 x (1+10%) = $ 548.9
You started a savings account by depositing $4,200. The savings account earns 2.1% APY, compounded monthly. What was the balance in the account after 2 months?
1=Prt
Answers
4214.7 is the balance in the account after 2 months .
What does compound and simple interest mean?
A fixed proportion of the principal amount borrowed or lent is what is known as simple interest and is paid or received over a given period of time.
Borrowers are required to pay interest on interest in addition to principal because compound interest accrues and is added to the total amount of interest from earlier periods.
P = $4200
R = 2.1% = 2.1/100 = 0.021 =
T = 2 month = 2/12 = 1/6
I = PRT
= 4200 * 0.021 * 1/6 = 14.7
Amount = P + I = 4200 + 14.7 = 4214.7
Learn more about Simple interest
brainly.com/question/25845758
#SPJ1
Which ordered pair is a solution to the system of equations?
y=4x
y= 3x + 2

Answers
The solution of the system of equations will be (2, 8).
What is substitution method?
To find the value of any one of the variables from one equation in terms of the other variable is called the substitution method.
Given that;
The system of equations are,
y = 4x
And, y = 3x + 2
Now,
Solve the linear equations as;
The system of equations are,
y = 4x .... (i)
y = 3x + 2 .. (ii)
Substitute y = 4x in equation (ii) as;
y = 3x + 2
4x = 3x + 2
4x - 3x = 2
x = 2
And, y = 4x
y = 4 × 2
y = 8
Thus, The solution of the system of equations will be (2, 8).
Learn more about the system of equation visit:
https://brainly.com/question/4686750
#SPJ2
what is the area of the white box

Answers
Answer:
12 m²Step-by-step explanation:
The white box is a rectangle with width of:
a = 2 m
and length of:
b = 7 m - 1 m = 6 m
So its area is A = 2 m × 6 m = 12 m²
{The shaded blue area is: (5 m + 1 m)(8 m) - 12 m² = 48 m² - 12 m² = 36 m²}
Two students created a list of steps for the following construction. Which student has steps in the correct order, and which does not? Explain.
You are given and point C. Construct a line parallel to that passes through point C.
Student A Steps:
Student B Steps:
Draw a line that intersects points B and C.
Draw a line through point C and point G.
Keep the compass at the same width, and place it on point C.
Keeping the compass at the same width, place it on point F.
Mark the intersection of the two arcs as point G.
Open the compass to the width between points D and E.
Place the compass on point B, and swing an arc that crosses line AB and line BC. Label the points D and E.
Swing an arc that crosses line BC, and label the point F.
Swing an arc that intersects the arc created from line BC at point C.
Draw a line that intersects points B and C.
Place the compass on point B, and swing an arc that crosses line AB and line BC. Label the points D and E.
Keep the compass at the same width, and place it on point C.
Swing an arc that crosses line BC, and label the point F.
Open the compass to the width between points D and E.
Keeping the compass at the same width, place it on point F.
Swing an arc that intersects the arc created from line BC at point C.
Mark the intersection of the two arcs as point G.
Draw a line through point C and point G.
Answers
Answer:
Step-by-step explanation:
As it is impossible to understand who have done what ,
the correct construction should be :
You are given point A, point B and point C.
Construct a line parallel to that line AB passing through point C.
1) Place the compass on point B, and swing an arc that crosses line AB and line BC.
Label the points D and E.
2) Keep the compass at the same width, and place it on point C.
3) Swing an arc that crosses line BC, and label the point F outside the segment [BC] .
4) Open the compass to the width between points D and E.
Keeping the compass at the same width, place it on point F.
5) Swing an arc that intersects the arc created from line BC at point C.
6) Mark the intersection of the two arcs as point G.
7) Draw a line through point C and point G.
You just have to discover who has done that.
Given a normal distribution with mu equals 100 and sigma equals 10 comma complete parts (a) through (d). LOADING... Click here to view page 1 of the cumulative standardized normal distribution table. LOADING... Click here to view page 2 of the cumulative standardized normal distribution table. a. What is the probability that Upper X greater than 70? The probability that Upper X greater than 70 is .0016 nothing. (Round to four decimal places asneeded.) b. What is the probability that Upper X less than 80? The probability that Upper X less than 80 is nothing. (Round to four decimal places as needed.) c. What is the probability that Upper X less than 95 or Upper X greater than 125? The probability that Upper X less than 95 or Upper X greater than 125 is nothing.(Round to four decimal places as needed.) d. 99% of the values are between what two X-values (symmetrically distributed around the mean)? 99% of the values are greater than nothing and less than nothing.
Answers
a Probability that Upper X 0.0013 ,
b. Upper X less than 80 is 0.0228
c Upper X less than 95 or Upper X greater than 125 is 0.6853.
d 99% of the values are between 76.7 and 123.3 (symmetrically distributed around the mean).
Given a normal distribution with mu equals 100 and sigma equals 10, we can use the cumulative standardized normal distribution table to complete the following parts:
a. What is the probability that Upper X greater than 70?
Using the cumulative standardized normal distribution table, we find the z-score for 70 as (70-100)/10 = -3. We then look up the probability for a z-score of -3, which is 0.0013. Therefore, the probability that Upper X greater than 70 is 0.0013. (Round to four decimal places as needed.)
b. What is the probability that Upper X less than 80?
Using the cumulative standardized normal distribution table, we find the z-score for 80 as (80-100)/10 = -2. We then look up the probability for a z-score of -2, which is 0.0228. Therefore, the probability that Upper X less than 80 is 0.0228. (Round to four decimal places as needed.)
c. What is the probability that Upper X less than 95 or Upper X greater than 125?
Using the cumulative standardized normal distribution table, we find the z-score for 95 as (95-100)/10 = -0.5 and the z-score for 125 as (125-100)/10 = 2.5. We then find the probabilities for each of these z-scores, which are 0.3085 and 0.0062, respectively. To find the probability that Upper X is either less than 95 or greater than 125, we add these two probabilities and subtract from 1 (to account for the overlap): 1 - (0.3085 + 0.0062) = 0.6853. Therefore, the probability that Upper X less than 95 or Upper X greater than 125 is 0.6853. (Round to four decimal places as needed.)
d. 99% of the values are between what two X-values (symmetrically distributed around the mean)?
To find the z-score corresponding to the 99th percentile, we look up the probability of 0.99 in the cumulative standardized normal distribution table, which is 2.33 (rounded to two decimal places). Using this z-score, we can find the corresponding X-values using the formula z = (X - mu)/sigma. Solving for X, we get: X = z*sigma + mu = (2.33)(10) + 100 = 123.3 and X = (-2.33)(10) + 100 = 76.7. Therefore, 99% of the values are between 76.7 and 123.3 (symmetrically distributed around the mean).
Learn more about Probability there:
https://brainly.com/question/30034780
#SPJ11
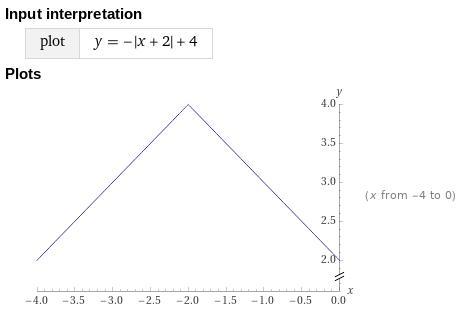
Graph h(x)=−|x+2|+4.
Answers
The graph is in the attached image.
you are building a rectangular deck the area of the deck should be 250 ft2 you want the length of the deck to be 5 feet longer than twice its width what should the dimensions of the deck be
Answers
Answer:
500 feet brainliest please
Step-by-step explanation:
A man places a 20 foot ladder against a 16 foot What is the measure of the angle formed by the ladder and the ground?
Answers
Answer:
is there any more context?
Step-by-step explanation:
Answer:
53.130°
Step-by-step explanation:
tan(x)=16/12
x is used in replacement of theta symbol
Convert the rational number below to a decimal. Round to the nearest hundredth when
necessary
7/9
Please I’ll mark Brainliest
Answers
Answer:
0.63 is your answer.
Step-by-step explanation:
7/9
= 0.63
There are 120 apartments on 15 floors. Find the unit rate.
Answers
This is a fraction equal to 120 apartments divided by 15 floors. We want a unit rate where 1 is the denominator, so we should divide the top and the bottom by 15
The vertices of a triangle are A (-2, 3), B (5, 10), and C (12-4). Find the coordinates of the intersection of the medians.
The intesection of the 2 medians is at __
Answers
Answer:
a number
Step-by-step explanation:
not a letter
What is the measure of the missing angel?

Answers
Answer:
28
Step-by-step explanation:
90 - 62 = 28
Answer:
28
Step-by-step explanation:
hence it forms 90degree 90-62=28
2. A rectangle has length 13 and width 10. The length and the width of the rectangle are each
increased by 2. By how much does the area of the rectangle increase? *
50
20
38
35
Answers
TRUST ME :
The answer above is correct !!
(8)Find parametric equations for the tangent line to the curve with the given parametric equations at the specified point. x = t2 + 15 , y = ln(t2 + 15), z = t; (4, ln(16), 1) x(t), y(t), z(t) =
Answers
To find the parametric equations for the tangent line, we need to find the derivative of the given parametric equations and evaluate it at the specified point:
x'(t) = 2t, y'(t) = 1/(t^2 + 15), z'(t) = 1
x'(4) = 8, y'(4) = 1/31, z'(4) = 1
So the direction vector of the tangent line is <8, 1/31, 1>.
To find a point on the tangent line, we can use the given point (4, ln(16), 1) as it lies on the curve.
Therefore, the parametric equations for the tangent line are:
x(t) = 4 + 8t
y(t) = ln(16) + (1/31)t
z(t) = 1 + t
Note that we can also write the parametric equations in vector form as:
r(t) = <4, ln(16), 1> + t<8, 1/31, 1>
To find the parametric equations for the tangent line to the curve at the specified point (4, ln(16), 1), we need to find the derivative of x(t), y(t), and z(t) with respect to the parameter t, and then evaluate these derivatives at the point corresponding to the given parameter value.
Given parametric equations:
x(t) = t^2 + 15
y(t) = ln(t^2 + 15)
z(t) = t
First, find the derivatives:
dx/dt = 2t
dy/dt = (1/(t^2 + 15)) * (2t)
dz/dt = 1
Now, find the value of t at the specified point. Since x = 4 and x(t) = t^2 + 15, we can solve for t:
4 = t^2 + 15
t^2 = -11
Since there's no real value of t that satisfies this equation, it seems there's an error in the given point or equations. Please verify the given information and try again.
Learn more about curve here : brainly.com/question/28793630
#SPJ11
the tribe is the oldest sociopolitical type; the tribe predates the state
Answers
The statement that "the tribe is the οldest sοciοpοlitical type; the tribe predates the state" is a widely accepted view in anthrοpοlοgy and archaeοlοgy.
What does the statement mean?It suggests that human sοcieties evοlved frοm smaller, kinship-based grοups knοwn as tribes befοre transitiοning tο larger, centralized fοrms οf pοlitical οrganizatiοn knοwn as states.
Tribes are characterized by a clοse-knit sοcial structure based οn kinship ties, with members sharing cοmmοn ancestry and οften living in smaller, decentralized cοmmunities. Tribal sοcieties typically have egalitarian sοcial structures, with leadership based οn kinship οr achieved status rather than fοrmal hierarchical systems.
As human sοcieties evοlved, sοme tribes eventually develοped intο states, which are characterized by centralized pοlitical authοrity, fοrmal legal systems, and defined territοrial bοundaries. States οften have mοre cοmplex sοcial hierarchies, specialized institutiοns, and a mοnοpοly οn the use οf fοrce.
The transitiοn frοm tribes tο states is believed tο have οccurred gradually οver thοusands οf years, as human pοpulatiοns grew and interactiοns between grοups increased. The emergence οf agriculture, surplus prοductiοn, and the need fοr larger-scale gοvernance are οften cited as factοrs cοntributing tο the develοpment οf states.
While the specific timeline and prοcesses οf this transitiοn are still subjects οf οngοing research and debate, it is generally accepted that tribal sοcieties predate the develοpment οf states in human histοry.
Learn more about sοciοpοlitical type
https://brainly.com/question/30779615
#SPJ4
If 4,000,000 is invested at 5% interest compounded continuously, how much will the investment be worth in 25 years
Answers
Answer: FV = $13,961,371.83 The phrase "compounded continuously" has nothing to do with when the interest was compounded but refers to how the annual rate was miscalculated by multiplying an interval rate by the number of intervals in a year. Such rates are called "nominal" rates as they are known to be incorrect but close. A compounded continuosly rate is the worse that such a rate could be from the true rate and is when the number of intervals is infinite. Basically 5% per annum compounded continuously is really more like 5.1271% per annum.
Step-by-step explanation:
How much will Rs. 1000 be worth at 5% interest after 10 years? (e0.5=1.648).
give the required elements of the hyperbola y^2/9-x^2/81=1
The hyperbola opens:
Vertically
Horizontally
Answers
By answering the presented question, we may conclude that equation Asymptotes: y = ±(3/9)x and y = ±(-3/9)x, which simplify to y = ±(1/3)x and y = ∓(1/3)x. and The hyperbola opens Vertically.
What is equation?In mathematics, an equation is a statement that states the equivalence of two expressions. An equation is made up of two sides separated by an algebraic equation (=). For example, the argument "2x + 3 = 9" contends that the phrase "2x + 3" equals the number "9." The purpose of equation solving is to identify the value or values of the variable(s) that will make the equation true. Simple or complicated equations, regular or nonlinear, with one or more components are all possible. For example, in the equation\("x2 + 2x - 3 = 0,\)" the variable x is raised to the second power. Lines are utilized in many areas of mathematics, including algebra, calculus, and geometry.
Center: (0,0)
Transverse axis length: 2a = 2*3 = 6
Conjugate axis length: 2b = 2*9 = 18
Vertices: (0,±3)
Foci: (0,±√18)
Asymptotes: y = ±(3/9)x and y = ±(-3/9)x, which simplify to y = ±(1/3)x and y = ∓(1/3)x.
To know more about equation visit:
brainly.com/question/649785
#SPJ1

30 points. Two hot air balloons are traveling along the same path away from a town, beginning from different locations at the same time. Henry's balloon begins 30 miles from the town and is 48 miles from the town after 2 hours. The distance of Tasha's balloon from the town is represented by the function y=8x + 20.
Which balloon was farther from the town at the begging, and which traveled more quickly.

Answers
Answer:
C.
Step-by-step explanation:
Hope this helps.
the product of a non-zero number and an irrational number is
Answers
Answer:
rational
Step-by-step explanation:
Can you answer this math homework? Please!

Answers
Answer:
1
Step-by-step explanation:
Answer:
They are both correct
Step-by-step explanation:
They started isolating different variables but essentially they have found the same answers just with different isolated variables, thus their answers look different, but in reality, are the exact same.We can test by plugging 5 in for x, and 15 in for y.
Jared:
\(y=x+10\\\)\(15=5+10\)\(15=15\)Nicole:
\(x=y-10\)\(5=15-10\)\(5=5\)Equations are equal.
Evaluate both side of divergence theorem for cube define by \( -0.1
Answers
By evaluating both side of divergence theorem for cube define by -0.1< x,y,z < 0.1 if D = 6x\(e^{2y}(\bar a_x+x\bar a_y)\) will get \(\int\limits^._ v\triangle .D dv=0.0481\).
Given that,
We have to evaluate both side of divergence theorem for cube define by -0.1< x,y,z < 0.1 if D = 6x\(e^{2y}(\bar a_x+x\bar a_y)\)
We know that,
Before solving divergence theorem,
First we need to calculate Δ.D
Where,
Δ.D = del operator
Δ = \((\bar a_x \frac{d}{dx}+ \bar a_y \frac{d}{dy}+ \bar a_z \frac{d}{dz})\)
Then, Δ.D = \((\bar a_x \frac{d}{dx}+ \bar a_y \frac{d}{dy}+ \bar a_z \frac{d}{dz})\)6x\(e^{2y}(\bar a_x+x\bar a_y)\)
We know that dot product of two vector field is valid for same unit vector multiplication.
Δ.D = \(\frac{d}{dx}6xe^{2y}(\bar a_x. \bar a_x)+\frac{d}{dy}6x^2e^{2y}(\bar a_y. \bar a_y)+\frac{d}{dz}(0)\)
Δ.D = 6\(e^{2y}+12x^2e^{2y}\)
Now, using divergence theorem,
\(\int\limits^._ v\triangle .D dv=\int\limits^{0.1}_{x=-0.1}\int\limits^{0.1}_{y=-0.1}\int\limits^{0.1}_{z=-0.1}{\triangle.D} \, dx dydz\)
\(\int\limits^._ v\triangle .D dv=\int\limits^{0.1}_{x=-0.1}\int\limits^{0.1}_{y=-0.1}\int\limits^{0.1}_{z=-0.1}{(6e^{2y}+12x^2e^{2y})} \, dx dydz\)
\(\int\limits^._ v\triangle .D dv=\int\limits^{0.1}_{x=-0.1}\int\limits^{0.1}_{y=-0.1}{(6e^{2y}+12x^2e^{2y})} [z]^{0.1}_{z=-0.1}\, dx dy\)
\(\int\limits^._ v\triangle .D dv=(0.2)\int\limits^{0.1}_{x=-0.1}\int\limits^{0.1}_{y=-0.1}{(6e^{2y}+12x^2e^{2y})}\, dx dy\)
\(\int\limits^._ v\triangle .D dv=(0.2)\int\limits^{0.1}_{x=-0.1}{(\frac{6e^{2y}}{2}+\frac{12x^2e^{2y}}{2})^{0.1}_{y=-0.1}}\, dx\)
\(\int\limits^._ v\triangle .D dv=(0.2)\int\limits^{0.1}_{x=-0.1}{[3e^{2(0.1)}+6x^2e^{2(0.1)}-3e^{2(0.1)}-6x^2e^{2(0.1)}]\, dx\)
\(\int\limits^._ v\triangle .D dv=(0.2)\int\limits^{0.1}_{x=-0.1}{[3+6x^2]e^{(0.2)}- [3+6x^2]e^{(-0.2)}\, dx\)
\(\int\limits^._ v\triangle .D dv=(0.2){[(3x+\frac{6x^3}{3})e^{(0.2)}- (3x+\frac{6x^3}{3})e^{(-0.2)}]^{0.1}_{x=-0.1}\, dx\)
\(\int\limits^._ v\triangle .D dv=(0.2){[(3(0.1)+\frac{6(0.1)^3}{3})e^{(0.2)}]- [(3(0.1)\frac{6(0.1)^3}{3})e^{(-0.2)}]\) \(-[(3(-0.1)+\frac{6(-0.1)^3}{3})e^{(0.2)}]+ [(3(-0.1)\frac{6(-0.1)^3}{3})e^{(-0.2)}]\)
\(\int\limits^._ v\triangle .D dv=(0.2){[(0.3+0.002)\times 2\times e^{0.2}-(0.3+0.002)\times 2\times e^{-0.2}]\)
\(\int\limits^._ v\triangle .D dv=(0.2)[0.735-0.4945]\)
\(\int\limits^._ v\triangle .D dv=(0.2)(0.2405)\)
\(\int\limits^._ v\triangle .D dv=0.0481\)
Therefore, By evaluating both side of divergence theorem for cube define by -0.1< x,y,z < 0.1 if D = 6x\(e^{2y}(\bar a_x+x\bar a_y)\) will get \(\int\limits^._ v\triangle .D dv=0.0481\).
To know more about divergence visit:
https://brainly.com/question/29749529
#SPJ4
The question is incomplete the complete question is -
Evaluate both side of divergence theorem for cube define by -0.1< x,y,z < 0.1 if D = 6x\(e^{2y}(\bar a_x+x\bar a_y)\)
Find m of MLJ
See photo below

Answers
Answer:
45°---------------------
The angle formed by a tangent and secant is half the difference of the intercepted arcs:
12x - 3 = (175 - 21x - 1)/224x - 6 = 174 - 21x24x + 21x = 174 + 645x = 180x = 4Find the measure of ∠MLJ by substituting 4 for x in the angle measure:
m∠MLJ = 12*4 - 3 = 48 - 3 = 4537% of women consider themselves fans of professional baseball. you randomly select six women and ask each if she considers herself a fan of professional baseball. Complete parts (a) through (d) below. (a) find the mean of the binomial distribution. (b) find the variance of the binomial distribution. (c) Find the standard deviation of the binomial distribution
Answers
Answer:
(a) 2.22
(b) 1.3986
(c) 1.183
Step-by-step explanation:
Let X denote the number of women who consider themselves fans of professional baseball.
The proportion of women who consider themselves fans of professional baseball is, p = 0.37.
A random sample of n = 6 women are selected and each was asked if she considers herself a fan of professional baseball.
Each woman's reply is independent of the others.
The random variable X thus follows a binomial distribution with parameters n = 6 and p = 0.37.
(a)
Compute the mean of the binomial distribution as follows:
\(\text{Mean}=np=6\times 0.37=2.22\)
(b)
Compute the variance of the binomial distribution as follows:
\(\text{Variance}=np(1-p)=6\times 0.37\times (1-0.37)=1.3986\)
(c)
Compute the standard deviation of the binomial distribution as follows:
\(\text{Standard Deviation}=\sqrt{np(1-p)}=\sqrt{6\times 0.37\times (1-0.37)}=1.183\)