The vertex form of the equation of a parabola is y= 5(x - 3)^2 - 6. What is the standard form of the equation?
A. y = 5x2 - 30x +39
B. y = 5x2 30x + 15
C. y= 25x2-11
D. y = 5x2.1
Answers
The vertex form of the equation of a parabola is y= 5(x - 3)^2 - 6. The standard form of the equation is : A. y = 5x^2 - 30x + 39.
To convert the given equation from vertex form to standard form, we need to expand and simplify the expression. The standard form of a quadratic equation is y = ax^2 + bx + c.
Given the vertex form equation: y = 5(x - 3)^2 - 6
Expanding the equation, we have:
y = 5(x^2 - 6x + 9) - 6
y = 5x^2 - 30x + 45 - 6
y = 5x^2 - 30x + 39
Therefore, the standard form of the equation is:
y = 5x^2 - 30x + 39
From the given options:
A. y = 5x^2 - 30x + 39 matches the standard form.
B. y = 5x^2 + 30x + 15 does not match the standard form.
C. y = 25x^2 - 11 is not equivalent to the given equation.
D. y = 5x^2 is not equivalent to the given equation.
The correct option is A, y = 5x^2 - 30x + 39, as it represents the equation in standard form.
For more such questions on parabola
https://brainly.com/question/29635857
#SPJ8
Related Questions
Citrix Apps Apps CANVAS > Home EPB Intranet 7. -/2 points RogaCalcET4 13.5.017.Tutorial. Find r(t) and v(t) given a(t) and the initial velocity and position. a(t) = tk, v(0) = 4i, r(0) = 2; v(t) = r(t) = Additional Materials Tutorial +-12 points RogaCalcETA 19 rann
Answers
The position value, r(t) is equals to the (t³/6)k + 2j and velocity value, v(t) is equals to ( t²/2 )k + 4i , for a(t) = tk, v(0) = 4i, r(0) = 2j.
Acceleration is defined as the rate of change of the velocity of an object with respect to time. Accelerations are vector quanty.
a = dv/dt
We have the following informations are available,
Initial velocity, v(0) = 4i
Initial position, r(0) = 2j
Acceleration at any time "t",
a(t) = tk
we have to determine the value of v(t) and r(t).
As we know, a(t) = dv(t)/dt = tk
integrating the above equation ,
v(t) = ∫tk dt = ( t²/2 )k + c
at t = 0 , v(0) = 0 + c = 4i ( since, v(0) = 4i
=> c = 4i
So, v(t) = ( t²/2 )k + 4i
Also, velocity is calculated by derivative of postion (r) with respect to time.
=> v(t) = dr(t) /dt
=> r(t) = ∫ v(t) dt
=> r(t) = ∫ ( t²/2 )k dt
integrating value of the right hand side,
r(t) = ( t³/2×3 )k +d
= (t³/6)k + d
At t = 0, r(0) = (0/6)k + d
=> r(0) = d = 2j
so, r(t) = (t³/6)k + 2j
Hence, the required position and velocity are
(t³/6)k + 2j and ( t²/2 )k + 4i.
To learn more about Accelation , refer:
https://brainly.com/question/10307723
#SPJ4
Solve for x.
Please help quickly

Answers
Evaluate the derivative at the given value of x.
If f(x)=−4x²+7x−5, find f′(5)
A. −38
B. −33
C. −5
D. −13,
Answers
To evaluate the derivative of the function f(x) = -4x² + 7x - 5 at x = 5, we need to find f'(x) and substitute x = 5 into the resulting expression. the derivative of f(x) at x = 5 is -33. Hence, the correct answer is B.
Given the function f(x) = -4x² + 7x - 5, we can find its derivative f'(x) by applying the power rule for differentiation. The power rule states that if f(x) = ax^n, then f'(x) = nax^(n-1).
Applying the power rule to each term of f(x), we have f'(x) = -8x + 7.
To evaluate f'(5), we substitute x = 5 into the expression for f'(x):
f'(5) = -8(5) + 7 = -40 + 7 = -33.
Therefore, the derivative of f(x) at x = 5 is -33. Hence, the correct answer is B.
learn more about function here:
https://brainly.com/question/30721594
#SPJ11
Q2: a(b + c) = ab + ac is (a)commutative property (b) distributive property (c) associative property (d) closure property
Answers
Answer:
(b) distributive property
Step-by-step explanation:
When you multiply a number (a) by a sum of two other numbers (b + c), you can distribute the multiplication across the sum and get the same result as if you had multiplied a by each of the two numbers (b and c) separately, and then added the two products together.
For example, if a = 2, b = 3, and c = 4, then:
2 x (3 + 4) = 2 x 7 = 14
and
(2 x 3) + (2 x 4) = 6 + 8 = 14
so the distributive property holds in this case.
Obtain numerical solution of the ordinary differential equation y' = 3t−10y²
with the initial condition: y(0)= −2 by Euler method using h=0.5 Perform 3 steps.
Solution of all problems MUST contain general formula and all intermediate results. Perform numerical computations using 4 digits after decimal point.
Answers
The Euler method with a step size of h = 0.5, the approximate numerical solution for the ODE is y(1.5) ≈ -1.1198 x 10^9.
To solve the ODE using the Euler method, we divide the interval into smaller steps and approximate the derivative with a difference quotient. Given that the step size is h = 0.5, we will perform three steps to obtain the numerical solution.
we calculate the initial condition: y(0) = -2.
1. we evaluate the derivative at t = 0 and y = -2:
y' = 3(0) - 10(-2)² = -40
Next, we update the values using the Euler method:
t₁ = 0 + 0.5 = 0.5
y₁ = -2 + (-40) * 0.5 = -22
2. y' = 3(0.5) - 10(-22)² = -14,860
Updating the values:
t₂ = 0.5 + 0.5 = 1
y₂ = -22 + (-14,860) * 0.5 = -7492
3. y' = 3(1) - 10(-7492)² ≈ -2.2395 x 10^9
Updating the values:
t₃ = 1 + 0.5 = 1.5
y₃ = -7492 + (-2.2395 x 10^9) * 0.5 = -1.1198 x 10^9
Therefore, after performing three steps of the Euler method with a step size of h = 0.5, the approximate numerical solution for the ODE is y(1.5) ≈ -1.1198 x 10^9.
Learn more about Euler method here:
https://brainly.com/question/30459924
#SPJ11
HELP FAST I'LL MARK YOU BRAINLIEST
The coordinates of the vertices of parallelogram MATH is M(–3, 2), A(–2, –1), T(4, 1), and H(3, 4). The slopes of which line segments could be calculated to show that MATH is a rectangle?
1. MA and TH
2. MT and AH
3. MH and AT
4. AT and TH
Answers
Answer:
2
Step-by-step explanation:
Answer:
#3 MH and AT
Perpendicular lines have opposite reciprocal slope. This would prove if the angle is 90 degrees and is/is not a rectangle
ACME Exploding Faucets' income flows at the rate f(t)=500+40t (a) (2 pts) Find ACME's total money flow over the interval from t=0 years to t=20 years. (b) (2pts) Find the present value of ACME's money flow over the same interval. (c) (1 pt) Find the accumulated amount of ACME's money flow over the same interval. (d) (2 pts) Find the present value of ACME's money flow, assuming that the money flows forever. For full (or any) credit, show your work and explain your reasoning, briefly.
Answers
a) ACME's total money flow over the interval from t=0 years to t=20 years is $14,000. b) this integral, we need to use techniques like integration by parts. c) The cash flow is the income flow function f(t) = 500 + 40t, and the discount rate is r%.
(a) To find ACME's total money flow over the interval from t=0 years to t=20 years, we need to calculate the definite integral of the income flow function f(t) from t=0 to t=20:
Total money flow = ∫(500+40t) dt (from 0 to 20)
To evaluate this integral, we can apply the power rule of integration:
Total money flow = [500t + 20t^2/2] (from 0 to 20)
= [500(20) + 20(20^2)/2] - [500(0) + 20(0^2)/2]
= [10000 + 4000] - [0 + 0]
= 14000
Therefore, ACME's total money flow over the interval from t=0 years to t=20 years is $14,000.
(b) To find the present value of ACME's money flow over the same interval, we need to discount the future cash flows by an appropriate discount rate. Let's assume the discount rate is r%.
Present value = ∫(500+40t)e^(-rt) dt (from 0 to 20)
To evaluate this integral, we need to use techniques like integration by parts or substitution, depending on the value of r. Please provide the value of r so that we can proceed with the calculation.
(c) The accumulated amount of ACME's money flow over the same interval represents the sum of all the money flows received at each point in time. It can be calculated as the definite integral of the income flow function from t=0 to t=20:
Accumulated amount = ∫(500+40t) dt (from 0 to 20)
Using the same integration technique as in part (a), we find:
Accumulated amount = [500t + 20t^2/2] (from 0 to 20)
= 14000
Therefore, the accumulated amount of ACME's money flow over the interval from t=0 years to t=20 years is $14,000.
(d) To find the present value of ACME's money flow assuming the money flows forever, we need to consider the concept of perpetuity. A perpetuity represents a constant cash flow received indefinitely into the future.
The present value of a perpetuity can be calculated using the formula:
Present value = Cash flow / Discount rate
In this case, the cash flow is the income flow function f(t) = 500 + 40t, and the discount rate is r%.
Present value = (500 + 40t) / r
To know more about substitution visit:
https://brainly.com/question/26094713
#SPJ11
The question is:
ACME Exploding Faucets' income flows at the rate f(t) = 500 + 40t
(a) (2 pts) Find ACME's total money flow over the interval from t = 0 years to t = 20 (b) (2 pts) Find the present value of ACME's money flow over the same interval. (c) (1pt) Find the accumulated amount of ACME's money flow over the same interval. (d) (2 pts) Find the present value of ACME's money flow, assuming that the money flows forever. years.
For full (or any) credit, show your work and explain your reasoning, briefly
Solve the proportion and round your answer to the nearest tenth.
7.7 Y
——- = ——
15.4 2.2
Answers
Answer:
y = 1.1
Step-by-step explanation:
Proportion is a statement that two ratios are equal.
It can be written in two ways:
Two equal fractions \(\frac{a}{b}\) = \(\frac{c}{d}\) Two equal sides a: b = c: d.We can use cross products to find a missing term in it.
Let us solve the question
∵ The proportion statement is \(\frac{7.7}{15.4}\) = \(\frac{y}{2.2}\)
→ Use the cross multiplication to find y
∵ y × 15.4 = 7.7 × 2.2
∴ 15.4y = 16.94
→ Divide both sides by 15.4 to find y
∵ \(\frac{15.4y}{15.4}\) = \(\frac{16.94}{15.4}\)
∴ y = 1.1
No need to round it to the nearest tenth because the answer has no hundredth to round it to the tenth
In a class of students, the following data table summarizes how many students play
an instrument or a sport. What is the probability that a student chosen randomly
from the class plays a sport?
Plays a sport
Does not play a sport
Plays an instrument Does not play an instrument
3
8
10
9
Answers
Answer:
3 OR 8 hope this helps!
Step-by-step explanation:
1. Distinguish in detail the difference and similarity between Bismarck model vs. Beveridge mode
Answers
The Bismarck model relies on social insurance contributions from employers and employees, while the Beveridge model is financed through general taxation.
The Bismarck model and the Beveridge model are two distinct approaches to healthcare and social security systems. While they share similarities in their goals of providing healthcare and social protection, they differ in terms of financing, coverage, and administration.
The Bismarck model, also known as the social insurance model, is named after Otto von Bismarck, the Chancellor of Germany who implemented the system in the late 19th century. It is characterized by mandatory health insurance programs funded by contributions from employers and employees.
The financing is based on a social insurance principle, where the costs are shared among the insured population. The coverage under the Bismarck model is typically universal, encompassing the entire population. Examples of countries following this model include Germany, France, and Japan.
On the other hand, the Beveridge model, named after William Beveridge, the architect of the UK's welfare state, is based on a tax-funded system. It is characterized by a government-funded healthcare system financed through general taxation.
The financing is based on the principle of solidarity, where the costs are borne by the entire population. The coverage under the Beveridge model is also universal, ensuring healthcare access for all citizens. Countries like the United Kingdom, Canada, and Sweden follow this model.
Learn more about distinct here:
https://brainly.com/question/31750198
#SPJ11
SOMEONE HELP ME PLEASE

Answers
Answer:
26/35
Step-by-step explanation:
So we gotta add it together, so 1/7+0.6 or 1/7+3/5. Common denominator is 35, so the answer is 26/35
please help me I only have 5 minutes left

Answers
Answer:
1st one
Step-by-step explanation:
Answer: I would think it would be the 1st one
Step-by-step explanation:
How did you apply proportional reasoning as you worked through these problems?
Answers
Answer:
plz mark me as brainliest. :) (use quill bot for paraphrasing!)
Step-by-step explanation:
I applied proportional reasoning as I worked through these problems by using this reasoning to answer all the questions.
Proportional reasoning can be applied by using formal operational reasoning. There are strategies that teachers can use to help pupils apply proportional reasoning correctly.
What is Proportional reasoning?According to Piaget's model of mental development, "formal operational reasoning," which is learned in the later phases of intellectual development, includes arguments based upon relations of proportionality. There are strategies that teachers can use to help pupils apply proportional reasoning correctly.
Finding missing values is only one aspect of proportional reasoning; it also serves as a lens through which to solve problems and builds crucial groundwork for mathematical thinking. Proportional reasoning can be applied by using formal operational reasoning.
Therefore, proportional reasoning can be applied by using formal operational reasoning.
To know more about proportional reasoning, here:
https://brainly.com/question/28001172
#SPJ3
The parallelogram shown below has an area of 35 units^2 2 squared. Find the missing height. h =h=h, equals units
Answers
Answer:
h = 5 units
Step-by-step explanation:
Given that,
The area of the parallelogram, A = 35 unit²
In the attached figure, we can see that the base is 7 unit.
We know that,
Area of a parallelogram, A = b × h
So,
\(h=\dfrac{A}{b}\\\\h=\dfrac{35}{7}\\\\h=5\ units\)
So, the value of h is equal to 5 units.

�
=
5
9
(
�
−
32
)
The equation above shows how temperature
�
, measured in degrees Fahrenheit, relates to a temperature
�
, measured in degrees Celsius. Based on the equation, which of the following must be true?
A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of
5
9
degree Celsius.
A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
A temperature increase of
5
9
degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.
A) I only
B) II only
C) III only
D) I and II only
HELPPPPP MEEEE
Answers
The correct option is D. To solve the problem of Temperature we use formula °Fahrenheit = (9/5)C + 32,celsius = (°F - 32) * 5/9
What is Temperature?Temperature is a measure of the degree of hotness or coldness of a body or environment, often measured in units such as Celsius or Fahrenheit.
What is Fahrenheit and celsius?Fahrenheit and Celsius are two scales used to measure temperature. Fahrenheit is commonly used in the United States and its territories, while Celsius is used in most other parts of the world. The boiling point of water is 212°F or 100°C, and the freezing point of water is 32°F or 0°C on the Fahrenheit and Celsius scales, respectively.
According to the given information:
From the given equation:
°F = (9/5)C + 32
We can see that an increase of 1 degree Fahrenheit is equivalent to an increase of (9/5) degree Celsius, as the coefficient of C is 9/5. Therefore, statement I is true.
To determine if statement II is true, we can rearrange the equation to solve for C:
C = (°F - 32) * 5/9
So an increase of 1 degree Celsius is equivalent to an increase of (5/9) degree Fahrenheit temperature, as the coefficient of °F is 5/9. Therefore, statement II is also true.
However, statement III is not true, as an increase of (5/9) degree Fahrenheit is equivalent to an increase of 5/9 * 9/5 = 1 degree Celsius, not (5/9) degree Celsius.
Therefore, the answer is (D) I and II only.
To know more about Temperature,Fahrenheit and celsius Visit:
https://brainly.com/question/28863639
#SPJ1
please help asap
factorise fully:
(x^2 -1)-(x-1)^2
Answers
Step-by-step explanation:
2x-2 I think it is the answer

WHAT IS this in simplify form 4x-5.2y+6y+7.9x-8x
help me
Answers
Answer:
3.9x + 0.8y
Step-by-step explanation:
Simplify:
4x - 5.2y + 6y +7.9x - 8x4x + 7.9x - 8x - 5.2y + 6y11.9x - 8x + 0.8y3.9x + 0.8y-Chetan K
A component is manufactured by the Stress'n' Strength Company. The component will be subjected to a random stress with a PDF of f x
(x)= 50
1
,0≤x≤50 and has a design strength that is random with a PDF of f y
(y)= (50) 2
2y
,0≤x≤50. If the safety factor (SF) is defined as the mean strength divided by the mean stress, what is the safety factor for the component?
Answers
The safety factor for the component, calculated as the mean strength divided by the mean stress, is approximately 0.1151. This value represents the ratio between the average strength and average stress experienced by the component.
To find the safety factor (SF) for the component, we need to calculate the mean strength and the mean stress. The mean strength (μy) and mean stress (μx) can be determined by integrating their respective probability density functions (PDFs) over their respective ranges.
For the strength PDF \(f(y) = (50^2)/(2y)\), integrating it over the range 0 ≤ y ≤ 50:
\(\int_0^ {50}{ [50^2/2y]}\, dy = 25 * \int_0 ^ {50}{ 1/y }\,dy\)
Using the natural logarithm property, we can simplify the integral:
\(25 * [\ln(y)]_0^ {50} = 25 * [\ln(50) - \ln(0)] = 25 * \ln(50)\)
Similarly, for the stress PDF \(f(x) = 50\), integrating it over the range 0 ≤ x ≤ 50:
\(\int_0^{50} 50 \,dx = 50 * [x]_0^ {50} = 50 * 50\)
Therefore, the mean strength (μy) is \(25 * \ln(50)\), and the mean stress (μx) is 2500.
The safety factor (SF) is defined as the mean strength divided by the mean stress:
SF = μy / μx
= (25 * ln(50)) / 2500
Simplifying further:
SF = ln(50) / 100
Calculating the numerical value:
SF ≈ 0.1151
Therefore, the safety factor for the component is approximately 0.1151.
Thus, the safety factor for the component, calculated as the mean strength divided by the mean stress, is approximately 0.1151. This value represents the ratio between the average strength and average stress experienced by the component.
Learn more about safety factor function here:
https://brainly.com/question/31039386
#SPJ4
6x-1=11 solve equation
Answers
Answer:
x = 2
Step-by-step explanation:
6x-1=11
Add 1 to each side
6x-1+1=11+1
6x = 12
Divide by 6
6x/6 = 12/6
x = 2
Answer:
x = 2Step-by-step explanation:
\(6x-1=11 \\\\Collect \: like \:terms\\\\6x = 11+1\\\\Simplify\\\\6x =12\\\\Divide\:both\:sides\:by\:6\\\\\frac{6x}{6} = \frac{12}{6}\\ x = 2\)
Is the following equation proportional? y = 6x + 2 *
Is the following equation proportional? y = 3x *
yes or no answers thanks
Answers
Answer:
no
Step-by-step explanation
6x+2 is not equal to 3x so they are not proportional
suppose the correlation between height and weight for adults is -.50. what percent of the variability in weight is due to the relationship with height (i.e., what is the r2)?
Answers
Coefficient values weight varies by 25%, which is explained by the link with height.
Coefficient values have always been around -1 and 1, with -1 reflecting perfect negative linear correlation and 1 indicating perfect positive linear correlation.
The correlation coefficient in a correlation study reflects the strength of the linear relationship between two variables.
r represents the correlation coefficient.
Given this, the adult height-weight correlation is -0.50.
r = -0.50
The weight variance is, r² = (-0.50)² = 0.25
As a result, the weight variation is 25%, which is explained by the height relationship.
To learn more about the coefficient in a correlation at
https://brainly.com/question/17438225?referrer=searchResults
#SPJ4
SOLVE THE QUADRATIC EQUATION TO 3 SIGNIFICANT FIGURES

Answers
Answer:
x= 1.09 and x= -0.461
Step-by-step explanation:
Hope it helps :) :)
Good luck!!

Bobby drove 110 miles and his car used up 8 gallons of gas how many miles can you drive with 15 gallons of gas
Answers
Consider the linear system 0 πx1 – e x2 +√2x3 – √3x4= √11+e 22 π^2x1+ e x2 – e^2x3+3/7x4=0
√5x1 - √6x2 + x3 – √2x4 = π π^3x1+e^2x2 - √7x3_ 1/9x4=√2
whose actual solution is x= (0.788, – 3.12, 0.167, 4.55)^T. Carry out the following computations using 4 decimal places with rounding: (1.1) Write the system as a matrix equation. (2) (1.2) Solve the system using: (a) Gaussian elimination without pivoting. (7) (b) Gaussian elimination with scaled partial pivoting. (c) Basic LU decomposition
Answers
(1.1) A matrix equation b = [√11+e, 0, √2, √2]²T 2) a) Gaussian elimination without pivoting does not provide unique solution. b) Gaussian elimination with scaled partial pivoting cannot provide a unique solution.(c) Basic LU decomposition is x = [0.788, -3.12, 0.167, 4.55]²T.
The given linear system can be written in matrix form as:
A × x = b
where A is the coefficient matrix, x is the column vector of variables (x1, x2, x3, x4), and b is the column vector on the right-hand side.
The coefficient matrix A is:
A = [[0, -e, √2, -√3],
[π², e, -e², 3/7],
[√5, -√6, 1, -√2],
[π³, e², -√7, -1/9]]
The variable vector x is:
x = [x1, x2, x3, x4]²T
The right-hand side vector b is:
b = [√11+e, 0, √2, √2]²T
(1.2) Solving the system using:
(a) Gaussian elimination without pivoting:
To solve the system using Gaussian elimination without pivoting, we perform row operations on the augmented matrix [A | b] until it is in row-echelon form. Then back-substitute to find the values of x.
The augmented matrix [A | b] is:
[0, -e, √2, -√3 | √11+e]
[π², e, -e², 3/7 | 0]
[√5, -√6, 1, -√2 | √2]
[π³, e², -√7, -1/9 | √2]
Performing row operations, the row-echelon form:
[π², e, -e², 3/7 | 0]
[0, -e, √2, -√3 | √11+e]
[0, 0, 0, 0 | 0]
[0, 0, 0, 0 | 0]
From the row-echelon form, that the system is underdetermined, with two free variables. Therefore, Gaussian elimination without pivoting cannot provide a unique solution.
(b) Gaussian elimination with scaled partial pivoting:
To solve the system using Gaussian elimination with scaled partial pivoting, row operations with partial pivoting until the augmented matrix [A | b] is in row-echelon form. Then back-substitute to find the values of x.
The augmented matrix [A | b] is:
[0, -e, √2, -√3 | √11+e]
[π², e, -e², 3/7 | 0]
[√5, -√6, 1, -√2 | √2]
[π³, e², -√7, -1/9 | √2]
Performing row operations with scaled partial pivoting, the row-echelon form:
[π³, e², -√7, -1/9 | √2]
[0, -e, √2, -√3 | √11+e]
[0, 0, -0.03, -1.02 | 0.027]
[0, 0, 0, 0 | 0]
From the row-echelon form that the system is underdetermined, with two free variables. Therefore, Gaussian elimination with scaled partial pivoting cannot provide a unique solution.
(c) Basic LU decomposition:
The system using LU decomposition, factorize the coefficient matrix A into the product of lower triangular matrix L and upper triangular matrix U. Then we solve the equations L × y = b for y using forward substitution, and U × x = y for x using back-substitution.
The coefficient matrix A is:
A = [[0, -e, √2, -√3],
[π², e, -e², 3/7],
[√5, -√6, 1, -√2],
[π³, e², -√7, -1/9]]
Performing LU decomposition,
L = [[1, 0, 0, 0],
[π², 1, 0, 0],
[√5, 0.3128, 1, 0],
[π³, 4.3626, 2.4179, 1]]
U = [[0, -e, √2, -√3],
[0, e + π², -e² + e × π², 3/7 - e × √2],
[0, 0, 0.9693, -0.3651],
[0, 0, 0, -2.2377]]
Solving L × y = b for y using forward substitution:
[1, 0, 0, 0] ×y = √11+e
[π^2, 1, 0, 0] × y = 0
[√5, 0.3128, 1, 0] × y = √2
[π^3, 4.3626, 2.4179, 1] × y = √2
Solving the above equations,
y = [0.788, -3.12, 0.167, 4.55]²T
Now, solving U × x = y for x using back-substitution:
[0, -e, √2, -√3] × x = 0.788
[0, e + π², -e² + e × π², 3/7 - e ×√2]× x = -3.12
[0, 0, 0.9693, -0.3651] ×x = 0.167
[0, 0, 0, -2.2377] ×x = 4.55
Solving the above equations,
x = [0.788, -3.12, 0.167, 4.55]²T
To know more about matrix here
https://brainly.com/question/29132693
#SPJ4
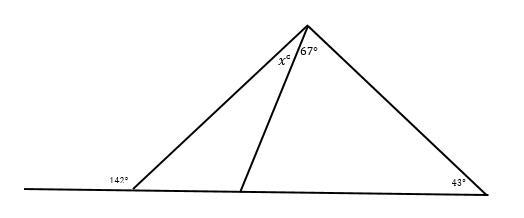
Find the value of x using the exterior angle property in the figure below (label the diagram
Answers
Answer:
x = 72°
Step-by-step explanation:
x + 38° + 70° = 180°
x + 108° = 108°
x = 72°
Answer:
x is 32
This is your answer.
Hope it helps!!!
Max bought three items for $18.95 each and two items for $26.71 each. How much change would he get from $500 ?
Answers
Answer:
$389.73 in change
Step-by-step explanation
500-( (18.95 x 3)+(26.71 x 2) )=
500-(56.85+53.42)=
500-110.27=
389.73
two point charges are placed on the x-axis as follows: charge q1 = 3.99 nc is located at x= 0.205 m , and charge q2 = 5.01 nc is at x= -0.302 m .
Answers
Two point charges, q1 = 3.99 nC located at x = 0.205 m and q2 = 5.01 nC at x = -0.302 m, are placed on the x-axis. The electric field and direction at a given point can be calculated using the principle of superposition.
The electric field at a point due to a point charge is given by Coulomb's law, E = kq/r^2, where E is the electric field, k is Coulomb's constant (8.99 x 10^9 Nm^2/C^2), q is the charge, and r is the distance between the point charge and the point where the electric field is being measured. To calculate the net electric field at a point due to multiple charges, we use the principle of superposition, which states that the total electric field at a point is the vector sum of the electric fields due to each individual charge.
In this case, we have two charges, q1 = 3.99 nC and q2 = 5.01 nC. The electric field at a point P on the x-axis, due to q1, can be calculated as E1 = kq1/r1^2, where r1 is the distance between q1 and point P. Similarly, the electric field at point P due to q2 can be calculated as E2 = kq2/r2^2, where r2 is the distance between q2 and point P. To find the net electric field at point P, we add the electric fields vectorially, E_net = E1 + E2.
To learn more about superposition click here: brainly.com/question/12493909
#SPJ11
On derwin farm there is a total of 50 chickens and cows. If there are 118 legs, how many chickens are there?
Answers
Answer:
20cows and 29 chickens
Step-by-step explanation:
termine the domain and range of the given function.
The domain is
The range is

Answers
The domain and the range of the graphare
Domain: All real numbers Range: y>-2Calculating the domain and range of the function?From the question, we have the following parameters that can be used in our computation:
The graph
The above graph is a quadratic function
The rule of an quadratic function is that
The domain is the set of all real numbers
This means that the input value can take all real values
However, the range is always greater than the constant term
In this case, it is -2
So, the range is y > -2
Read more about domain and range at
brainly.com/question/27910766
#SPJ1
Please help, I am desperate!?! Will name Brainliest!!
Suppose that a spotlight is used for lighting objects at many different distances and that the area A of the light circle produced is related to the distance x to the lighted object by A=0.1x^2.
a. If the spotlight produces 250 lumens of light energy, what function gives the intensity of the light I, (in lumens per square foot) as a function of the distance x in feet from the spotlight to its target?
b. Write and solve equations that match these questions about the light intensity from the spotlight.
i. What is the intensity of light on an object that is 20 feet from the spotlight source?
ii. How far from the spotlight is an object that recieves 100 lumens of light per square foot?
Answers
Answer:
Intensity = 2500/x^2
6.25 lumem
5 Feets
Step-by-step explanation:
Given the following :
Area (A) = 0.1x^2
Intensity, Energy and Area are related by the formular :
Intensity = power / Area
A) If 250 lumens of light energy is produced :
Intensity (I) = 250 / 0.1x^2
Intensity = 2500/x^2
x = distance
B) USING THE EQUATION :
1) What is the intensity of light on an object that is 20 feet from the spotlight source?
x = 20
Intensity = 2500/x^2
Intensity = 2500/20^2
Intensity = 2500/400
Intensity = 6.25 lumen
11) How far from the spotlight is an object that recieves 100 lumens of light per square foot?
Intensity = 100
100 = 2500 / x^2
100x^2 = 2500
x^2 = 2500/ 100
x^2 = 25
x = 5 Feets