Tristan bought a shirt that usually sells for $75 but is on sale for 20% off. How much did he pay for the shirt?
Answers
20% of 75 is 15
75 - 16 = 60
he paid $60 for the shirt
please give brainliest
Related Questions
Consider the following data drawn independently from normally distributed populations: (You may find it useful to appropriate table: z table or t table)
xˉ1 = −17.1
s1^2 = 8.4
n1=22
xˉ2 = −16.0
s2^2 = 8.7
n2 = 24
a. Construct the 90% confidence interval for the difference between the population means. Assume the population va unknown but equal. (Round final answers to 2 decimal places.)
confidence interval is __ to __
Answers
The 90% confidence interval for the difference in the population means is -2.51 to 0.31
Calculating the 90% confidence interval for the population mean differenceFrom the question, we have the following parameters that can be used in our computation:
xˉ₁ = −17.1
s₁² = 8.4
n₁ = 22
xˉ₂ = −16.0
s₂² = 8.7
n₂ = 24
Calculate the pooled variance using
P = (df₁ * s₁² + df₂ * s₂²)/df
Where
df₁ = 22 - 1 = 21
df₂ = 24 - 1 = 23
df = 22 + 24 - 2 = 44
So, we have
P = (21 * 8.4 + 23 * 8.7)/44
P = 8.56
Also, we have the standard error to be
SE = √(P/n₁ + P/n₂)
So, we have
SE = √(8.56/22 + 8.56/24)
SE = 0.86
The z score at 90% CI is 1.645, and the CI is calculated as
CI = (x₁ - x₂) ± z * SE
So, we have
CI = (-17.1 + 16.0) ± 1.645 * 0.86
This gives
CI = -1.1 ± 1.41
Expand and evaluate
CI = (-2.51, 0.31)
Hence, the confidence interval is -2.51 to 0.31
Read more about confidence interval at
https://brainly.com/question/15712887
#SPJ1
how large a sample should be taken in order to estimate the proportion to within 4% with a 95.44% level of confidence?
Answers
Answer: The product of two consecutive negative integers is 600. What is the value of the lesser integer?
Step-by-step explanation:
EDGE2021
An event A will occur with probability 0.4. An event B will occur with probability 0.7. The probability that both A and B will occur is 0.2. The conditional probability of A. given B, is O 0.17. O 0.20. O 0.29. O unable to be determined from the information given.
Answers
Rounding this value, we get P(A|B) ≈ 0.29. Thus, the correct answer is 0.29.
To answer this question, we need to find the conditional probability of A given B, which is represented as P(A|B). We are given the probabilities of event A and event B occurring, as well as the probability of both events occurring. We can use this information to calculate P(A|B) using the formula:
\(P(A|B) = P(A ∩ B) / P(B)\)
Here, P(A ∩ B) represents the probability of both events A and B occurring, and P(B) represents the probability of event B occurring. We are given the following information:
- P(A) = 0.4
- P(B) = 0.7
- P(A ∩ B) = 0.2
Now we can plug these values into the formula to calculate P(A|B):
\(P(A|B) = 0.2 / 0.7 = 0.2857\)
for such more questions on probability
https://brainly.com/question/24756209
#SPJ11
Advanced conversions:
4 L=
mL
570 mL =
L
5 cm =
mm
135 mm =
cm
5 mg =
cg
1820 mg =
25 mL =
L
0.5 g =
cg
0.125 g =
mg
0.2385 mL =
L

Answers
Answer:
Step-by-step explanation:
1). ∵ 1 L = 1000 ml
∴ 4 L = 4000 ml
2). ∵ 1 cm = 10 mm
∴ 5 cm = 50 mm
3). ∵ 1 mg = 0.1 cg
∴ 5 mg = 0.5 cg
4). ∵ 1 ml = 0.001 L
∴ 25 ml = 0.025 L
5). ∵ 1 gm = 1000 mg
∴ 0.125 gm = 25 mg
6). ∵ 1 ml = 0.001 L
∴ 570 ml = 0.57 L
7). ∵ 1 mm = 0.1 cm
∴ 135 mm = 13.5 cm
8). ∵ 1 mg = 0.001 g
∴ 1820 mg = 1.82 g
9). ∵ 1 g = 100 cg
∴ 0.5 g = 50 cg
10). ∵ 1 ml = 0.001 L
∴ 0.2385 ml = 0.0002385 L
yeah These points are linear.Find the slope.x-2-1 0 1 1 2y -7 0 7 14 21slope = [?]-
![yeah These points are linear.Find the slope.x-2-1 0 1 1 2y -7 0 7 14 21slope = [?]-](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/ZdaFPEbh6QlYKiOMHptwa4iimR1ar1Mb.jpeg)
Answers
slope=7
Explanation
the slope of a line ( or segment) is given by
\(\begin{gathered} \text{slope}=\frac{\text{ change in y }}{\text{ change in x}}=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1} \\ \text{where} \\ P1(x_1,y_1)\text{ } \\ \text{and} \\ P2(x_2,y_2) \\ \text{are 2 points from the line} \end{gathered}\)so
Step 1
Let
\(\begin{gathered} P1(0,7) \\ P2(2,21) \end{gathered}\)now,replace in the formula
\(\begin{gathered} \text{slope}=\frac{y_2-y_1}{x_2-x_1} \\ \text{slope}=\frac{21-7}{2-0}=\frac{14}{2}=7 \end{gathered}\)therefore, the slope is 7
I hope this helps you
Calculate the perimeter of this right- angled triangle. Give your answer in metres (m) to 1 d.p. 7m 16 m

Answers
Answer:
P = 37.4 m
Step-by-step explanation:
let the third side of the triangle be x
using Pythagoras' identity in the right triangle.
x² + 7² = 16²
x² + 49 = 256 ( subtract 49 from both sides )
x² = 207 ( take square root of both sides )
x = \(\sqrt{207}\) ≈ 14.4 m ( to 1 decimal place )
the perimeter (P) is then the sum of the 3 sides
P = 7 + 16 + 14.4 = 37.4 m
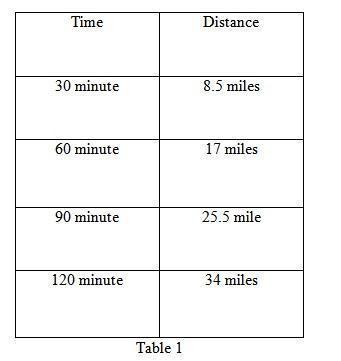
randon enters bike races. He bikes 91 half miles every1 half hour. Complete the table to find how far Brandon bikes for each time interval. (ignore the numbers in the boxes i put them and they were incorrect)

Answers
Answer:
It is given that in every 1/2 hours Brandon bikes .
The distance 8 1/2 miles is in the form of mixed fraction.
Therefore, the distance 8 1/2 miles can be written in the form of decimal as follows:
8 1/2 miles = 8.5 miles
Brandon bike's 8.5 miles in every 1/2 hours .
We know that 1 hour is equivalent to 60 minutes .
So, 0.5 hours can be converted into minutes as follows:
1 hour = 60 minutes
1.5 hours= 30 minutes
Therefore, in every 30 minutes Brandon bikes .
So, in next 30 minutes Brandon also bikes 8.5 miles .
In every 1 hour Brandon travels = 8.5+8.5 = 17 miles.
In every 1:30 Brandon travels 17 +8.5 =25.5 miles.
Method 2:
Speed of Brandon’s bike can be calculated as ,
speed = distance/time
Here, d is the distance and t is the time.
Now, substitute d=8.5 and t= 0.5 in the equation (1)
Therefore, the rate of travelling of Brandon’s bike is .
The distance of Brandon’s bike in each interval of time can be represented in the attached Table 1.Hope this helps you!!!!!!!!!!!!!!!!!!!!!
which expression is equivalent to 4 (9 + 7)
Answers
4(9+7) = 36+28 = 64
open the parentheses, then simplify.
A project under consideration costs \( \$ 500,000 \), has a five-year life and has no salvage value. Depreciation is straight-line to zero. The firm has made the following projections related to this
Answers
The project has a net present value of $100,000, an internal rate of return of 15%, and a profitability index of 1.1. Therefore, the project should be accepted.
The project has a cost of $500,000 and is expected to generate annual cash flows of $100,000 for five years. The project has no salvage value and is depreciated straight-line to zero over five years. The firm's required rate of return is 10%.
The net present value (NPV) of the project is calculated as follows:
NPV = -500,000 + 100,000/(1 + 0.1)^1 + 100,000/(1 + 0.1)^2 + ... + 100,000/(1 + 0.1)^5
= 100,000
The internal rate of return (IRR) of the project is calculated as follows:
IRR = n[CF1/(1 + r)^1 + CF2/(1 + r)^2 + ... + CFn/(1 + r)^n] / [-Initial Investment]
= 15%
The profitability index (PI) of the project is calculated as follows:
PI = NPV / Initial Investment
= 1.1
The NPV, IRR, and PI of the project are all positive, which indicates that the project is financially feasible. Therefore, the project should be accepted.
Learn more about profitability here: brainly.com/question/29987711
#SPJ11
would your confidence intervals of parts a and c be valid if the distribution of the original population were not normal?
Answers
The 95% confidence interval for μ is (80.52, 82.68).
To find the 95% confidence interval for the population mean (μ), we can use the following formula
CI = X ± z* (σ / √n)
where X is the sample mean, σ is the population standard deviation (unknown), n is the sample size, and z* is the critical value from the standard normal distribution corresponding to the desired confidence level (in this case, 95%).
The critical value z* can be found using a standard normal distribution table or calculator, or using a statistical software. For a 95% confidence level, the z* value is 1.96.
Plugging in the values given, we get
CI = 81.6 ± 1.96 × (5.4 / √100)
Simplifying this expression, we get
CI = 81.6 ± 1.08
= (80.52, 82.68)
Learn more about confidence interval here
brainly.com/question/24131141
#SPJ4
The given question is incomplete, the complete question is:
A random sample of 100 observations from a normally distributed population possesses a mean equal to 81.6 and a standard deviation equal to 5.4 . Find a 95% confidence interval for μ
Jason is playing a game. He has two sets of cards. One set has three red cards, numbered 1, 2 and 3. The other set has four green cards, numbered 4, 5, 6 and 8. Jason chooses a red card and a green card at random. He works out his score by adding the numbers on the two cards together. A sample space diagram is drawn below. Work out the probability that Jason gets a score of 9 or more.

Answers
Answer:
1/3
Step-by-step explanation:
There are 12 different sums.
4 of the sums are 9, 9, 10, 11.
All other sums are 8 or less.
p(9 or more) = 4/12 = 1/3
14. The maximum capacity for seating in a theater is 500 people. The theater sells two types of
tickets, adult tickets for $7.25 each and child tickets for $4 each. If they sold out on a certain
showtime and made a total of $3,157 in ticket sales, how many of each type of ticket was sold for
that showtime?
Answers
Taking into account the definition of a system of linear equations, the amount of adult tickets sold is 356 and the amount of child tickets sold is 144.
System of linear equationsA system of linear equations is a set of two or more equations of the first degree, in which two or more unknowns are related.
Solving a system of equations consists of finding the value of each unknown so that all the equations of the system are satisfied. That is to say, the values of the unknowns must be sought, with which when replacing, they must give the solution proposed in both equations.
Amount of ticket soldIn this case, a system of linear equations must be proposed taking into account that:
"x" is the amount of adult tickets sold."y" is the amount of child tickets sold.The maximum capacity for seating in a theater is 500 people. If they sold out on a certain showtime, this is represented by x+y=500.
On the other side, the theater sells two types of tickets, adult tickets for $7.25 each and child tickets for $4 each and the made a total of $3,157. This is represented by 7.25x +4y=3157.
So, the system of equations to be solved is
\(\left \{ {{x+y=500} \atop {7.25x+4y=3157}} \right.\)
There are several methods to solve a system of equations, it is decided to solve it using the substitution method, which consists of clearing one of the two variables in one of the equations of the system and substituting its value in the other equation.
In this case, isolating the variable x from the first equation you get:
x=500 - y
Substituting this expression in the second equation you get:
7.25× (500 -y) +4y=3157
7.25×500 - 7.25y +4y=3157
3625 - 7.25y +4y=3157
- 7.25y +4y=3157 -3625
-3.25y= -468
y= (-468)÷ (-3.25)
y= 144
Substituting this value in the expression x=500 - y you get:
x=500 - 144
x=356
Remembering that "x" is the amount of adult tickets sold and "y" is the amount of child tickets sold, you get that the amount of adult tickets sold is 356 and the amount of child tickets sold is 144.
Learn more about system of equations:
brainly.com/question/14323743
brainly.com/question/1365672
brainly.com/question/20533585
brainly.com/question/20379472
(1 point) 5 dice of different colors are rolled, and the number coming up on each die is recorded. how many different outcomes are possible? your answer is :
Answers
There are 7776 different outcomes possible when 5 dice of different colors are rolled.
What is probability?The ratio of favorable outcomes to the total number of outcomes of an event is said to be the probability of that event.
P(E) = n(E)/n(S)
Calculation:It is given that, there are 5 dice with different colors.
There are 6 outcomes for each die rolling. That is the number coming up on each die when it is rolled (1, 2, 3, 4, 5, 6).
So, for five dice when rolled, the number of possible outcomes is
n = 6 × 6 × 6 × 6 × 6
⇒ n = 7776
Therefore, 7776 different outcomes are possible.
Learn more about the probability of rolling a die here:
https://brainly.com/question/21459155
#SPJ4
Which choice is equivalent to the expression shown? 1 2(x + 4) 6 + 3 A) * + (B + 3 2x 5 C + 9 * D دیا | با

Answers
The answer is B.
7. Statistics is a branch of mathematics that deals with
A. graphing functions on a coordinate plane.
B. using artificial intelligence to make predictions.
C. collecting data about the world.
O D. the properties of shapes and space.
Answers
Statistics is a branch of mathematics that deals with collecting data about the world. Hence, option C is the correct answer.
What is statistics?The study of data gathering, analysis, interpretation, presentation, and organization is known as statistics. In other words, gathering and summarizing data is a mathematical discipline. Additionally, statistics might be considered a subfield of applied mathematics. However, uncertainty and variation are two crucial and fundamental concepts in statistics. Only statistical analysis can determine the uncertainty and variation in many sectors. The probability, which is a key concept in statistics, essentially determines these uncertainties.
According to the definition of statistics; the study of data gathering, analysis, interpretation, presentation, and organization is known as statistics.
Hence, statistics is a branch of mathematics that deals with collecting data about the world. Hence, option C is the correct answer.
Learn more about statistics here:
https://brainly.com/question/29342780
#SPJ1
https://lamar.schoolobjects.com/eduphoria_webcontrols/attachmentwriter.aspx?orgguid=9267358f-cea3-413e-9ad1-b591dccc7264&attid=fe4b0fa8-610f-4118-9330-307fd0edc9ba
Answers
Answer:
ok
Step-by-step explanation:
What is the best estimate of 31 3/4 X 4 1/7 = ? Help Me?!!

Answers
The best estimate of fraction is 131.445.
What is fractions?An element of a whole is a fraction. The number is represented mathematically as a quotient, where the numerator and denominator are split. Both are integers in a simple fraction. A fraction appears in the numerator or denominator of a complex fraction. The numerator of a proper fraction is less than the denominator. A fraction is a number that is a component of a whole. By breaking a whole into a number of parts, it is evaluated. For instance, the symbol for half of a complete number or item is \(\frac{1}{2}\)
Given Data
31\(\frac{3}{4}\) × 4\(\frac{1}{7}\)
Solving mixed fractions
\(\frac{127}{4}\) × \(\frac{29}{7}\)
31.75 × 4.14
Multiplying
131.445
The best estimate of fraction is 131.445.
To learn more about fractions, visit:
https://brainly.com/question/10354322
#SPJ9
Here is a list of numbers:
-16, -20, -10, 1, -10, 5, 0 ,8 ,2 ,-7
State the median.
Answers
Answer:
-3.5
Step-by-step explanation:First you need to order the numbers so the numbers ordered would be -20,-16,-10-,10-,7,0,1,2,5,8 the median is finding the middle number in a list so you would cross of the end numbers until you are left -7 and 0 you then find the mid point of these two numbers which is -3.5 so that would be the answer.
Answer:
The median is -3.5
Step-by-step explanation:
hope this helps
-16, -20, -10, 1, -10, 5, 0 ,8 ,2 ,-7
Arrange the number in numerical order.
-20,-16,-10,-10,-7,0,1,2,5,8
There's two number is the middle which is -7 and 0 all you have to do is add them together and divide by 2.
-7+0= -7÷2=-3.5
can I have help please
Alpha Exercise 2α Write down the ratio of vowels to consonants in each of the given words. Simplify your ratio where possible.
a) PLAN
b) NUMBER
c) RATIO
d) SHAPE
e) GRAPH
f) EQUALS
g) INVERSE
h) SCALE
i) PRIME
j) MATHEMATICS
k) VERTEX
l) MULTIPLE
m) FACTOR
n) ROTATION
o) REFLECTION
p) TRANSLATION
q) ENLARGEMENT
r) TRANSFORMATIONS
s) SIMULTANEOUS
t) CUMULATIVE
Answers
Consonants are the rest of the letters of the alphabet (e.g. b, c, y)
Ratios are comparisons of two or more amounts. For example if I have 2 eggs and 5 pens, the ration of eggs to pens would be 2:5. Ratios can also be simplified. An example could be if I had 10 eggs and 50 pens my first ratio would be 10:50. To simplify this you must find the highest common factor and divide BOTH of the numbers by it. In 10:50, you would get 1:5 when you divide both sides by 10.
So (a) has 1 vowel and 4 consonants. The ration would be 1:4.
(B) has 2 vowels and 4 consonants. The ration would be 2:4 which can be simplified to 1:2.
IMPORTANT: make sure to not swap the sides of the numbers. It should be vowels:consonants, not consonants:vowels.
Hope this helped.
write the equation in spherical coordinates. (a) 5z2 = 6x2 + 6y2
Answers
In spherical coordinates, the equation \(5z^2 = 6x^2 + 6y^2\) can be written as: \(ρ^2sin^2(φ) = 6ρ^2sin^2(θ)cos^2(φ) + 6ρ^2sin^2(θ)sin^2(φ)\)
What is Spherical coordinates?Spherical coordinates are a system of coordinates used to represent points in three-dimensional space. In this coordinate system, a point is described by three parameters: ρ (rho), θ (theta), and φ (phi).
ρ (rho) represents the radial distance from the origin to the point.
θ (theta) represents the azimuthal angle, which is the angle measured in the xy-plane from the positive x-axis to the line connecting the origin and the point.
φ (phi) represents the polar angle, which is the angle measured from the positive z-axis to the line connecting the origin and the point.
In spherical coordinates, a point in 3D space is represented using three parameters: ρ (rho), θ (theta), and φ (phi).
ρ (rho) represents the radial distance from the origin to the point.
θ (theta) represents the azimuthal angle, which is the angle measured in the xy-plane from the positive x-axis to the line connecting the origin and the point.
φ (phi) represents the polar angle, which is the angle measured from the positive z-axis to the line connecting the origin and the point.
To express the equation\(5z^2 = 6x^2 + 6y^2\)in spherical coordinates, we need to convert the variables x, y, and z to their corresponding spherical coordinate representations.
In spherical coordinates, the conversions are as follows:
x = ρsin(φ)cos(θ)
y = ρsin(φ)sin(θ)
z = ρcos(φ)
Substituting these values into the equation, we have:
5(ρcos(φ))^2 = 6(ρsin(φ)cos(θ))^2 + 6(ρsin(φ)sin(θ))^2
Simplifying the equation further by expanding the terms and using trigonometric identities, we can obtain the equation in spherical coordinates:
\(ρ^2sin^2(φ) = 6ρ^2sin^2(θ)cos^2(φ) + 6ρ^2sin^2(θ)sin^2(φ)\)
This equation relates the variables ρ, θ, and φ in spherical coordinates and represents the same relationship as the original equation in Cartesian coordinates.
To know more about Spherical coordinates refer here:
https://brainly.com/question/4465072
#SPJ4
If m∠KLJ = 78° then m∠OFG = _m∠OFG = __°

Answers
If angle m∠KLJ = 78° then m∠OFG = 78°.
The angle o a straight line
An angle is the parent shaped by using rays, referred to as the edges of the attitude, sharing a not unusual endpoint, referred to as the vertex of the attitude. Angles shaped via two rays lie inside the plane that includes the rays. Angles are also shaped through the intersection of two planes. those are known as dihedral angles.
The angle in a straight line says that the sum of all the angles on a straight line is 180°.
opposite vertical angle is the two opposite angles on a parallel line at the point of intersection.
angle ∠KLJ = 78°° (opposite vertical angle).
The angle on a straight line is 180°
angle∠OFG = 78°.
angle ∠KLJ =∠OFG = 78°. (parallel angles)
Learn more about angles here:-https://brainly.com/question/25716982
#SPJ9
At a dairy farm two cows produce enough milk to fill seven equal sized buckets. What is the rate of buckets per cow?
Answers
Answer: 3.5 buckets
Step-by-step explanation:
seven divided by 2 is 3.5
is it possible to create multiple triangles given 3 side lengths that meet the criteria outlined in the triangle inequality theorem? Explain.
Answers
Does anyone know this?

Answers
Answer:
So the formula will turn out to be 1.50 x 35 + 5, plug that into a calculator and you get 57.5. Therefore, your answer is $57.50.
graph the equation (x - 3)^2 + (y - 2)^2 = 25 and y = 6.
Answers
Answer:
x=6, x=0
Step-by-step explanation:
\((x - 3) ^{2}\)+ \((y - 2) ^{2}\)= 25
\((x - 3) ^{2}\)+ \((6 - 2) ^{2}\)= 25
x=6, x=0
Pls can u answer this.. and also ima post another one if h can answer that too ❣

Answers
Answer:
Hamid: 4
Ken: 3
Step-by-step explanation:
Start by finding the LCM (least common multiple) of 80 and 60. To do this we can list all the multiples of 80 and 60 until we get a common multiple.
60: 60, 120, 180, 240
80: 80, 160, 240
They both have a common multiple of 240, so after 240 seconds they will meet again at the start line.
Now we need to find how many laps they'll have to run. To do this we can divide 240 by the amount of time it takes for them to run a lap.
240/60=4
240/80=3
Hamid will have ran 4 laps and Ken will have ran 3 laps
Let A
be any language, define A13−13
be the subset of strings of A
whose middle third is removed.
The solution I came across makes the following claim, which I cannot justify: Let A={0∗#1∗}
then A13−13∩{0∗1∗}={0n1n∣n≥0}
. For example consider the string w=0000#1
, removing the middle third will yield 00#1
and whose intersection with {0∗1∗}
is ∅
which not of the form {0n1n∣n≥0}
.
Answers
The intersection A13−13∩{0∗1∗} is not equal to {0n1n∣n≥0}.
How to find the claim?The claim that A13−13∩{0∗1∗}={0n1n∣n≥0} is not correct.
To see why, let us consider a counterexample. Take the string w = "0000#1000". The middle third of w is "0#1", so the string obtained by removing the middle third is "000011000". This string is not in {0n1n∣n≥0}, as there are more 0s than 1s. However, "000011000" is in A13−13, as it can be written as "0000#1000" with the middle third removed.
Therefore, the intersection A13−13∩{0∗1∗} is not equal to {0n1n∣n≥0}.
Learn more about the intersection
brainly.com/question/12089275
#SPJ11
Using (x + a) (x + b) = x² + (a + b) x + ab, evaluate 75 x 77
Answers
(x + a) (x + b) = x² + (a + b) x + ab
75 * 77=
=(70+5)(70+7)
=70²+(5+7)*70+5*7
=4900+12*70+35
=4900+840+35
=5775
Review the table of values showing the number of
days each year from 1990 to 1997 that air quality in
San Diego did not meet federal air quality standards.

Answers
Answer: B
Step-by-step explanation: I got it right.
Answer:
GUYS THE PERSON ABOVE ME IS WRONG THE ANSWER IS NOT B IT IS C TRUST ME
Find the mode for the following data set:10 30 10 36 26 22
Answers
In this particular data set, 10 is the only value that occurs more than once, so it is the only mode
The mode is the value that occurs most frequently in a data set. In the given data set {10, 30, 10, 36, 26, 22}, we can see that the value 10 occurs twice, and all other values occur only once. Therefore, the mode of the data set is 10, since it occurs more frequently than any other value in the set.
Note that a data set can have multiple modes if two or more values occur with the same highest frequency. However, in this particular data set, 10 is the only value that occurs more than once, so it is the only mode.
To learn more about frequently visit:
https://brainly.com/question/13959759
#SPJ11