⦁ Two times the sum of eight and a number equal twelve.
write as an inequality
Answers
Hope this helps!
Related Questions
Lauren has a garden in the shape of a rectangle where the length is 5.4 meters and 1.5 meters. She plans on increasing both the length and width by 40%
Answers
Answer:
5.4 = 7.56
1.5 = 2.1
Step-by-step explanation:
Just find the answer for 40% of the given meters.
Order of Operations with and without variables

Answers
Answer:
9
Step-by-step explanation:
3 (2²) - 2(2) + 1 =
3 (4) - 4 + 1 =
12 - 4 + 1 =
8 + 1 = 9
Can someone help me pls
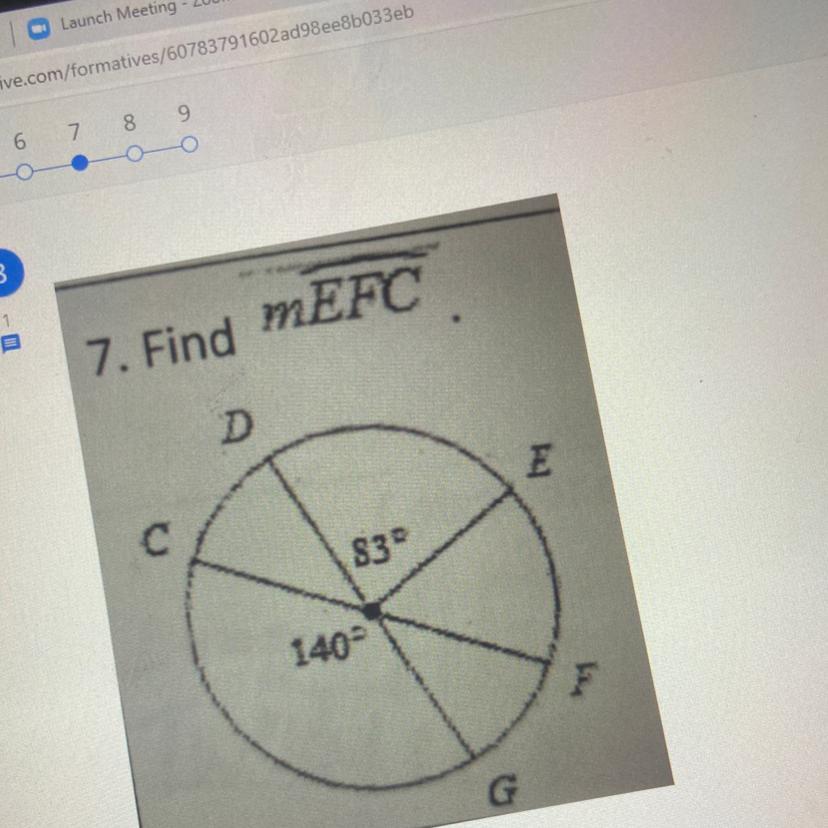
Answers
Answer:
\( m\overset{\Large\frown}{EFC} = 237° \)
Suppose a deck of cards contains 13 cards:
5 green cards numbered 1-5, 4 red cards numbered 1-4, and 4 blue cards numbered 1-4.
For 3.1-3.3, 5 draws are made without replacement. X is the number of green cards drawn and Y is the number of red cards drawn. Z is the sum of the numbers on the tickets.
G1 = first card is green
G2 = second card is green
Enter the probability as a fraction.
P(at least one green) = ______.
Answers
Answer:
\(P(G_1) = \frac{5}{13}\)
\(P(G_2) = \frac{1}{3}\)
\(P(X \ge 1) = \frac{25}{39}\)
Step-by-step explanation:
Given
\(G = 5\)
\(R = 4\)
\(B = 4\)
\(n = 13\)
Solving (a): \(P(G_1)\)
This is calculated as:
\(P(G_1) = \frac{G}{n}\)
\(P(G_1) = \frac{5}{13}\)
Solving (b): \(P(G_2)\)
This is calculated as:
\(P(G_2) = \frac{G - 1}{n - 1}\) -- this is so because the selection is without replacement
\(P(G_2) = \frac{5 - 1}{13 - 1}\)
\(P(G_2) = \frac{4}{12}\)
\(P(G_2) = \frac{1}{3}\)
Solving (c): \(P(X \ge 1)\)
Using the complement rule, we have:
\(P(X \ge 1) = 1 - P(X = 0)\)
To calculate \(P(X = 0)\), we have:
\(G = 5\) --- Green
\(G' = 8\) ---- Not green
The probability that both selections are not green is:
\(P(X = 0) = P(G'_1) * P(G'_2)\)
So, we have:
\(P(X = 0) = \frac{G'}{n} * \frac{G'-1}{n-1}\)
\(P(X = 0) = \frac{8}{13} * \frac{8-1}{13-1}\)
\(P(X = 0) = \frac{8}{13} * \frac{7}{12}\)
Simplify
\(P(X = 0) = \frac{2}{13} * \frac{7}{3}\)
\(P(X = 0) = \frac{14}{39}\)
Recall that:
\(P(X \ge 1) = 1 - P(X = 0)\)
\(P(X \ge 1) = 1 - \frac{14}{39}\)
Take LCM
\(P(X \ge 1) = \frac{39 -14}{39}\)
\(P(X \ge 1) = \frac{25}{39}\)
Find all solutions of each equation on the interval 0≤ x <2pie
tan² x sec² x +2 sec²x - tan²x =2
Answers
The trigonometric equations has the following solutions: x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.
How to solve a trigonometric equation
In this problem we find the case of a trigonometric equation, whose solutions on the interval [0, 2π] must be found. This can be done by both algebra properties and trigonometric formulae. First, write the entire expression:
tan² x · sec² x + 2 · sec² x - tan² x = 2
Second, use trigonometric formulas to reduce the number of trigonometric functions:
tan² x · (tan² x + 1) + 2 · (tan² x + 1) - tan² x = 2
Third, expand the equation:
tan⁴ x + tan² x + 2 · tan² x + 2 - tan² x = 2
tan⁴ x + 2 · tan² x = 0
Fourth, factor the expression:
tan² x · (tan² x - 2) = 0
tan² x = 0 or tan² x = 2
tan x = 0 or tan x = ± √2
Fifth, determine the solutions to trigonometric equation:
x = 0 + j · π or x = 0.352π + j · π or x = - 0.352π + j · π, where j is a non-negative whole number.
To learn more on trigonometric equations: https://brainly.com/question/22624805
#SPJ1
Find the equation with vertex(-2,5) and focus(1,5)
Answers
Answer:
\((y-5)^2=12(x+2)\)
Step-by-step explanation:
Since the focus point is directly right of the vertex, the axis of symmetry will be horizontal, which means that we use the equation \((y-k)^2=4p(x-h)\) where \((h,k)\) is the vertex and \((h+p,k)\) is the focus point.
Since we know our vertex to be \((h,k)\rightarrow(-2,5)\) and our focus point to be \((h+p,k)\rightarrow(1,5)\), the distance from the vertex to the focus point is \(p=3\).
Hence, the equation is:
\((y-5)^2=4(3)(x-(-2))\\\\(y-5)^2=12(x+2)\)

There are 25 popular trees currently in the park. Park workers will plant morepopular trees today. When the workers are finished there will be 80popular trees in the park. How many popular trees did the workers plant today?
Answers
Current trees = 25
trees when workers are finished = 80
Subtract the number of current trees (25) to the number of trees that are when the workers are finished:
80-25 = 55
The workers planted 55 trees today
Graph the following function: y=−sec(x+π/4)+2
Answers

24 as a prime factor from smallest to largest
Answers
Answer:
it's prime factors are; 1, 2 ,3, 3, 5, 7, 11, 13, 19, 23
find the value of x using the kite below (work required)

Answers
Since the diagonals in a kite intersect creating a right angle, the angles 2x° and (10x - 6)° are complementary angles. So we have:
\(\begin{gathered} 2x+(10x-6)=90 \\ 12x-6=90 \\ 12x=96 \\ x=\frac{96}{12} \\ x=8 \end{gathered}\)So the value of x is 8.
Find the area of the triangle

Answers
Answer:
i don’t know sorry
Step-by-step explanation:
nothing
A soda can has a radius of 1 inch and a height of 5 inches and a density of 3.2 g/mL. What is the mass?
Answers
The mass of the soda can is given by the formula M = V*d, where d is the density of the soda can. Substituting the given values, we get M = 15.708 cubic inches * 3.2 g/mL = 50.226 g.
Therefore, the mass of the soda can is approximately 50.226 grams.
Enter the number that belongs in the green box
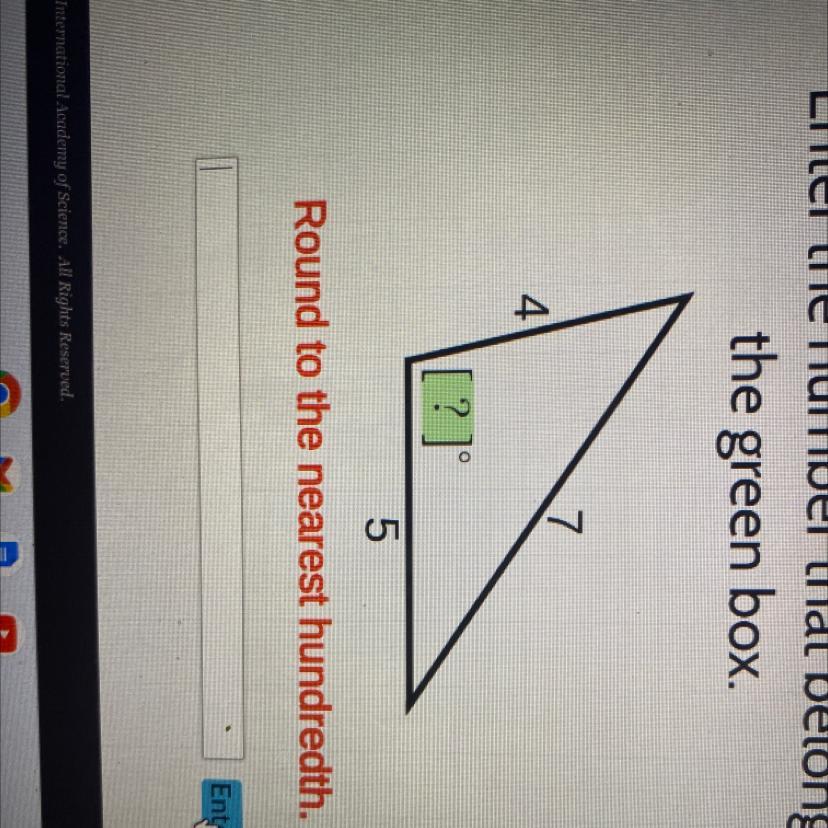
Answers
The angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
To find the measure of the angle between the sides measuring 4 and 5 in an obtuse triangle with side lengths 4, 5, and 7, we can use the Law of Cosines. The Law of Cosines states that in a triangle with side lengths a, b, and c, and an angle opposite to side c, the following equation holds:
\(c^2 = a^2 + b^2 - 2ab*cos(C)\)
In this case, we have side lengths a = 4, b = 5, and c = 7. We want to find the angle C, which is opposite to side c. Substituting these values into the Law of Cosines, we get:
\(7^2 = 4^2 + 5^2\)- 2(4)(5)*cos(C)
49 = 16 + 25 - 40*cos(C)
49 = 41 - 40*cos(C)
40*cos(C) = 41 - 49
40*cos(C) = -8
cos(C) = -8/40
cos(C) = -0.2
To find the measure of angle C, we can take the inverse cosine (arccos) of -0.2:
C = arccos(-0.2)
Using a calculator, we find that C ≈ 101.54 degrees.
Therefore, the measure of the angle between the sides measuring 4 and 5 in the obtuse triangle is approximately 101.54 degrees.
For more such information on: angle
https://brainly.com/question/25716982
#SPJ8
2. Given a can of soda with a radius of 1 inch and a height of 6.2 inches,what is the volume? Use 3.14 for n.19.5 in³9.7 in³39 in³4.9 in³
Answers
We need to assume that the can of soda can be represented as a cylinder. Then we use the formula for a cylinder volume and that's it.
The volume of a cylinder is given by:
\(v=\pi r^2\times h\)Where r is the radius of the base and h the height of the can.
If we reply the measures in this equation we have:
\(v=\pi(1in)^2\times6.2in=19.468\text{ in}^3\)So we can conclude that the volume of the can of soda is 19.5 in³, thus the correct answer is A.
7y - 2y + 8 = 19 + 4y
Answers
7y - 2y + 8 = 19 + 4y
7y - 2y - 4y = 19 - 8
1y = 19 - 8
1y = 11
Ans is y = 11
(6.2 x 10²) x (3.5 x 10³)
Answers
Answer:
\(21.7 x 10^5\)
Step-by-step explanation:
(6.2 x 10²) x (3.5 x 10³)
First, multiply the coefficients: 6.2 x 3.5 = 21.7.
Then, add the exponents: 10² x 10³ = 10^(2+3) = 10^5.
Therefore, the result is 21.7 x 10^5.
Answer:
3286000
Step-by-step explanation:

Hans baked b cookies. His family ate 20 of them. Using b, write an expression for the number of cookies that remained.
Answers
Number of cookies = b
Number of cookies the family ate = 20
number of cookies left = ?
Number of cookies = Number of cookies ate + number of cookies that remained
b = 20 + number of cookies that remained
To get the number of cookies that remained, we'll subtract 20 from both sides:
\(\begin{gathered} b\text{ - 20 = 20 - 20 + number of cookies that remained} \\ b\text{ - 20 = number of cookies that remained} \end{gathered}\)An expression showing number of cookies remaining:
\(\text{number of cookies that remained = }b\text{ - 20 }\)The county fair charges $1.25 per ticket for the rides. Jermaine bought 25 tickets for the rides and spent a
total of $43.75 at the fair. Jermaine spent his money ONLY on ride tickets and fair admission. The price of the
fair admission is the SAME for everyone. Use y to represent the total cost and x to represent the number of
ride tickets
(a) Using the information provided for Jermaine, what is the price of the fair admission? Show all steps
for full credit.
(b) Using the x and y as defined in the problem, write a linear equation that can be used to determine the
cost for anyone who only pays for ride tickets and fair admission.
Step 1: Identify the slope and y-intercept for the equation.
Step 2: Write the equation in slope-intercept form.
Answers
Answer:
a) Price of admission is $12.50
b) linear equation: 1.25x + 12.5 = y
slope: 1.25
y-intercept: 12.5
The equation above is in slope-intercept form
Here's the work step by step :)
hope it helps!
Step-by-step explanation:
$1.25 is the cost per ticket
Jermaine bought 25 tickets in total
Spent a total of $43.75
y = total cost
x = number of ride tickets
1.25 ( 25 ) = 31.25
31.25 is the total money spent on ONLY tickets.
To find the cost of admission...
43.75 - 31.25 = 12.50
The cost of admission is $12.50
Equation: 1.25x + 12.5 = y
(1.25 is the cost per ticket and 12.5 is the intial charge/admission fee and y is the total cost)
y = mx + b
m= slope and b= y - intercept
1.25x + 12.5 = y
slope: 1.25
y - intercept: 12.5
Solve the exponential equation for x. 3^3x-2 = 9^4x-1 x=
Answers
The solution of the exponential equation 3^(3x-2) = 9^(4x-1) is x = 0.
We can solve this exponential equation for x by using logarithms. We can take the logarithm of both sides of the equation, using any base that we prefer. For instance, we can use the natural logarithm, ln:
ln(3^(3x - 2)) = ln(9^(4x - 1))
Now, we can use the properties of logarithms to simplify both sides of the equation. First, recall that ln(a^b) = b ln(a), for any positive value of a and any real value of b. Therefore, we have:
(3x - 2) ln(3) = (4x - 1) ln(9)
Next, we can use another property of logarithms, namely ln(a^b) = b ln(a) = ln(c) → a^b = c, to eliminate the natural logarithms from both sides of the equation. Specifically, we can rewrite ln(9) as ln(3^2), and then use the power rule for logarithms, ln(a^b) = b ln(a), to get:
(3x - 2) ln(3) = (4x - 1) ln(3^2) = 2 (4x - 1) ln(3)
Now, we can simplify the equation by multiplying out the coefficients of ln(3) on the left-hand side:
3x ln(3) - 2 ln(3) = 8x ln(3) - 2 ln(3)
Then, we can collect like terms:
3x ln(3) - 8x ln(3) = -2 ln(3) + 2 ln(3)
Finally, we can solve for x by factoring out ln(3) and dividing both sides by the resulting factor:
(3 ln(3) - 8 ln(3)) x = 0
-5 ln(3) x = 0
x = 0
Therefore, the solution of the exponential equation 3^(3x-2) = 9^(4x-1) is x = 0.
To learn more about exponential function visit:
brainly.com/question/29506679
#SPJ1
Bob needs at least $90 to purchase some items for his sports team. He makes $6 an hour mowing lawns in his neighborhood, and he has $13 saved. Which of the inequalities represents the situation, if h is the number of hours Bob mows the lawn?
Answers
Initial amount saved = $13
Total amount earned for working h hours at $6 per hour = 6h
Total amount in $ Bob will have = 6h + 13
The required inequality is
\(6h+13\ge90\)The correct option is the last option
What is the total surface area

Answers
Answer:
Step-by-step explanation:

Suppose the manufacturer of a board game will supply 10,000 games if the wholesale price is $1.50 each but will supply only 5000 if the price is $1.00 each. Assuming that the supply function is linear, write its equation. Use p for price and q for quantity.
Answers
The equation of the supply function is q = 20000p - 10000
How to determine the equation of the supply functionLet's use the point-slope form of a linear equation:
slope = (change in quantity) / (change in price) = (10000 - 5000) / (1.50 - 1.00) = 10000 / 0.50 = 20000
Using the point-slope form with the point (1.50, 10000):
q - 10000 = 20000(p - 1.50)
Simplifying:
q = 20000p - 20000 + 10000
q = 20000p - 10000
So the equation of the supply function is q = 20000p - 10000
Learn more about supply function at https://brainly.com/question/12959332
#SPJ1
A drawer is filled with 9 black shirts, 6 white shirts, and 4 gray shirts. One shirt is chosen at random from the drawer. Find the probability that it is not a gray shirt. Write your answer as a fraction in simplest form.
Answers
Step-by-step explanation:
Total shirts = 19
Probebility of not gray = 19 - 4 = 15
if not gray it should be black and white..
Than probebility of not gray is 15/ 19=0.78
Approx....
Distribute to create an equivalent expression with the fewest symbols possible.
4(5+y) =4(5+y)
Answers
The equivalent expression of 4(5+y) by distributing is 20 + 4y.
How to find equivalent expression?In maths, an expression is a combination of numbers, variables, functions (such as addition, subtraction, multiplication or division etc.).
Two expressions are said to be equivalent if they have the same value irrespective of the value of the variable(s) in them.
In other words, two mathematical expressions are said to be equivalent if they yield the same result upon solving them.
Therefore, let's find the equivalent expression of 4(5 + y) by distributing it.
Hence,
4(5 + y) = 20 + 4y
learn more on equivalent expression here: https://brainly.com/question/29412493
#SPJ1
(c) Problem 17:
How far will the baseball have dropped after
4.5 seconds?
(first taught in
lesson 90)
Afton
Answers
After 4.5 seconds, the baseball will have dropped approximately 99.35 meters.
To find out how far the baseball will have dropped after 4.5 seconds, we need to use the free fall formula.
The terms involved in this calculation are:
Time (t): 4.5 seconds.
Acceleration due to gravity (g): 9.81 m/s² (approximated)
Distance dropped (d)
The free fall formula is:
\(d = (1/2) \times g \times t^{2}\)
Now, we will plug in the given values and solve for d:
Substitute the values
\(d = (1/2) \times 9.81 \times (4.5)^{2}\)
Calculate the square of time
\(d = (1/2) \times 9.81 \times 20.25\)
Multiply the values
d = 99.3525.
For similar question on free fall formula.
https://brainly.com/question/3522016
#SPJ11
2) Ayanda wants to invest R200 000. The bank offers him 2 options for his
6 year investment.
Option 1: 12% Simple interest p.a.
Option 2: 9,5% Compound interest p.a.
4.2.1) Calculate the return on Ayanda's investment using Option 1.
●
●
4.2.2) Calculate the return on Ayanda's investment using Option 2.
4.2.3) Which option will render the most money?
Answers
Answer:
4.2.1) R140 000
4.2.2) R144 758.28
4.2.3) Option 2
Step-by-step explanation:
To calculate the return on Ayanda's investment using Option 1, we can use the simple interest formula.
\(\boxed{\begin{minipage}{7 cm}\underline{Simple Interest Formula}\\\\$ I =Prt$\\\\where:\\\\ \phantom{ww}$\bullet$ $I =$ interest accrued \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}\)
Given values:
P = R200 000r = 12% = 0.12t = 6 yearsSubstitute the given values into the formula and solve for I:
\(I=200000 \cdot 0.12 \cdot 6\)
\(I=24000 \cdot 6\)
\(I=144000\)
Therefore, the return on Ayanda's investment using Option 1 is R144000.
\(\hrulefill\)
To calculate the return on Ayanda's investment using Option 2, we can use the compound interest formula.
\(\boxed{\begin{minipage}{7 cm}\underline{Annual Compound Interest Formula}\\\\$ I=P\left(1+r\right)^{t}-P$\\\\where:\\\\ \phantom{ww}$\bullet$ $I =$ interest accrued \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}\)
Given values:
P = R200 000r = 9.5% = 0.095t = 6 yearsSubstitute the given values into the formula and solve for I:
\(I=200000(1+0.095)^6-200000\)
\(I=200000(1.095)^6-200000\)
\(I=200000(1.72379142...)-200000\)
\(I=344758.28426...-200000\)
\(I=144758.28426...\)
\(I=144758.28\)
Therefore, the return on Ayanda's investment using Option 2 is R144758.28.
\(\hrulefill\)
Comparing the returns from both options, we find that Option 1 offers a return of R144000, while Option 2 offers a return of R144758.28. As R144758.28 > R144000, then Option 2 will render the most money for Ayanda's investment.
At a meeting, there were 18 men and 24 women. What is the ratio of men to women at the meeting?
Answers
Answer:
18:24
Step-by-step explanation:
There is 18 men and they are at the beginning of the problem so the 18 men go first then the 24 Women.
The admission fee at a park is $1.25 for children and $5.40 for adults. On a certain day, 319 people entered the park, and the admission fees collected totaled $1125. How many children and how many adults were admitted?
Answers
Answer:
So 900 children went that day and
225 adults went that day
Step-by-step explanation:
1125 divided by 1.25=900 children
so then if you want to find out adults then just subtract
1125-900=225 adults
Hope this helped and Have a great day!!!
What is the first step in evaluating the expression below 3x{9-(4+2)/2
Answers
The first step in evaluating the expression 3x{9-(4+2)/2 is to simplify the innermost parentheses. By performing operations within parentheses first, we can simplify the expression and make it easier to evaluate.
To begin, we evaluate the expression within the parentheses (4+2), which equals 6. Thus, the original expression becomes 3x{9-6/2}.
The next step is to simplify the division operation. We divide 6 by 2, resulting in 3. Now the expression becomes 3x{9-3}.
The subsequent step is to simplify the subtraction operation. We subtract 3 from 9, giving us 6. The expression now becomes 3x6.
Finally, we multiply 3 by 6, yielding a final result of 18. Therefore, the evaluation of the expression 3x{9-(4+2)/2 is equal to 18.
By simplifying the parentheses, performing the division, and evaluating the subtraction, we systematically reduce the expression to its simplest form. Following the order of operations (also known as PEMDAS or BODMAS), which prioritizes parentheses, exponents, multiplication and division (from left to right), and addition and subtraction (from left to right), ensures an accurate evaluation of the expression.
For more questions on BODMAS
https://brainly.com/question/24383445
#SPJ8
Bazinga charges $16.50 per hour to dogsit. Complete the table and answer the questions below.
number of hours
charge in dollars
1
16.50
49.50
6
199.00
132.00
8
A Write an expression describing Bazinga's earnings for working h hours.

Answers
#A
No preliminary values so no y intercept
rate of change =16.5
Equation
y=mxy=16.5x#2
4-1/2=4.5hours
Put 4.5 in equation
y=16.5(4.5)y=74.25$#3
Let y be 115.5
Now
16.5x=115.5x=115.5/16.5x=7hoursAnswer:
A) c = 16.5h
B) $74.25
C) 7 hours
Step-by-step explanation:
Bazinga charges $16.50 per hour to dog sit.
Therefore, to calculate the total charge, multiply the number of hours by the charge per hour:
\(\large \begin{array}{| c | c |}\cline{1-2} \sf number\:of\:hours & \sf charge\:in\:dollars\\\cline{1-2} 1 & 16.50 \\\cline{1-2} 3 & 49.50 \\\cline{1-2} 6 & 99.00 \\\cline{1-2} 8 & 132.00 \\\cline{1-2}\end{array}\)
Part AAs explained above, to calculate the total charge, multiply the number of hours worked by the charge per hour of $16.50
⇒ c = 16.5h
where:
h = number of hours workedc = total charge (in dollars)Part BTo calculate how much Bazinga will earn if they dog sit for 4.5 hours, substitute h = 4.5 into the equation and solve for c:
⇒ c = 16.5h
⇒ c = 16.5(4.5)
⇒ c = $74.25
Part CTo calculate how long it will take Bazinga to earn $115.50, substitute c = 115.5 into the equation and solve for h:
⇒ c = 16.5h
⇒ 115.5 = 16.5h
⇒ h = 115.5 ÷ 16.5
⇒ h = 7 hours