what iis 5.46 ÷ 0.25 (show ur work)
Answers
Answer:
21.84
Step-by-step explanation:
5.46/0.25 is actually just 5.46 * 4 but an easier way to do this is just doing
5.46 * 2 which is 10.92
.46 + .46 is .92
5+5 is 10
so thats 10.92
and since we only did times 2 we have to double it
so 10.92 + 10.92
10 + 10 is 20
.92 + .92 is 1.84
20 + 1.84 is 21.84
2 1 . 8 4
2 5 | 5 4 6 .
5 0
------------------------------
4 6 .
2 5 .
-------------------------------
2 1 . 0
2 0 . 0
-----------------------------------
1 . 0 0
1 . 0 0
Therefore, 5.46 divided by 0.25 = 21.84.
Related Questions
Somebody help me solve these asap!!!

Answers
The firefighters cannot rescue the person if the angle measure is 55°.
Given that there is a fire fighters bus having a height of 8 ft is set to rescue at height of 75 ft from the ground with a ladder of 84 ft,
They set the ladder at an angle of 55°, we need to see if they can rescue with this measurement of angle or not,
So,
The actual height of the building if we do not include the height of the bus = 75 - 8 = 67 ft,
Now,
Using the trigonometric ratios,
We will calculate the ideal measure of the angle so that they can rescue,
So,
Let the angle be x,
Sin x = 67 / 84
x = Sin⁻¹ (67 / 84)
x = 52.90°
Therefore, the ideal angle to rescue the person in the building is 52.90° and not 55°.
Hence, they cannot rescue the person if the angle measure is 55°.
Learn more about height and distance click;
https://brainly.com/question/9965435
#SPJ1
Ms. Kay is putting $450 in the bank for 7 years. The bank has a rate of 5%. How much will she earn in interest?
Answers
Answer:
7*450*.5%
Step-by-step explanation:
(0)
Question 2 Consider the dynamic system described by Equation Q2. 85.16400 083.3770 0046.999 ⃗+ 0.079400 00.7030 001.07 ×10⃗+ 0.013600 03.1390 005.124 ×10⃗= 0 0 0 Equation Q2 (a) Calculate the spectral matrix, the undamped natural frequencies and damping ratios of the system in Equation Q2. Identify its fundamental frequency. (b) The following mode shape vectors have been used to diagonalise the equations of motion of the dynamical system presented in Equation Q2: f1 = [0.8076 1.0000 0.8039]T; f2 = [-0.9694 -0.1620 1.0000]T and f3 = [-0.5342 1.0000 -0.3523]T. Calculate the respective matrix of mass normalised mode shapes. (c) Using the mode superposition method, calculate the response of the system for the first physical coordinate y1 assuming the following initial conditions expressed in terms of the modal coordinates: the initial modal displacements are [0 0.5 0]T m and the initial modal velocities are [0 -3 0]T m/s.
Answers
The first physical coordinate y1 can be expressed as y1 = [1 0 0]Y, & The mass-normalised mode shapes can be normalising the mode shape vectors f1, f2, and f3.
Part (a)
In Equation Q2, the spectral matrix, undamped natural frequencies, damping ratios, and fundamental frequency need to be calculated.
The mass matrix is given by [85.16400 083.3770 0046.999; 0.079400 00.7030 001.07 × 10; 0.013600 03.1390 005.124 × 10].
The stiffness matrix is given by [0.16400 00.3770 000.999; 0.079400 00.7030 001.07 × 10; 0.013600 03.1390 005.124 × 10].
The damping matrix is given by [0 0 0; 0 0 0; 0 0 0].The undamped natural frequencies, damping ratios, and fundamental frequency for the system in Equation Q2 can be calculated from the spectral matrix.
The characteristic equation can be written as det(K-mω^2M)=0.where K is the stiffness matrix, M is the mass matrix, ω is the angular frequency, and m is the mass-normalised mode shape.
The roots of this equation are the undamped natural frequencies, and the damping ratios can be calculated from the undamped natural frequencies and mode shapes.
The mass-normalised mode shapes can be calculated by normalising the mode shape vectors f1, f2, and f3.
Part (b)
The mass-normalised mode shapes can be calculated using the mode shape vectors f1, f2, and f3.Part (c)The response of the system for the first physical coordinate y1 can be calculated using the mode superposition method. The initial modal displacements and velocities are given in terms of the modal coordinates.
The response is then calculated using the equation y(t)= Σ ai φi(t), where ai are the modal amplitudes, and φi(t) are the modal shapes given by the mode shape vectors f1, f2, and f3.
The first physical coordinate y1 can be expressed as y1 = [1 0 0]Y, where Y is the vector of physical coordinates. The modal amplitudes can be calculated from the initial modal displacements and velocities.
Learn more about coordinate from the given link
https://brainly.com/question/17206319
#SPJ11
Does anyone know how to fill this out?

Answers
Which polynomial function has zeros when x=-2,3/4,5?
A f(x)=(x-2)(3x+4)(x+5)
B f(x)=(x-2)(4x+3)(x+5)
C
f(x)=(x+2)(3x-4)(x+5)
D f(x)=(x+2)(4x-3)(x-5)
Answers
The polynomial function has zeros when x=-2,3/4,5 is option D f(x)=(x+2)(4x-3)(x-5), according to the question.
What do you mean by function?
A function in mathematics from a set X to a set Y assigns exactly one element of Y to each element of X. The sets X and Y are collectively referred to as the function's domain and codomain, respectively.
According to the given question,
We have the given options are:
A f(x)=(x-2)(3x+4)(x+5)
B f(x)=(x-2)(4x+3)(x+5)
C f(x)=(x+2)(3x-4)(x+5)
D f(x)=(x+2)(4x-3)(x-5)
We will putting given x=-2,3/4,5 in the given functions one by one,
Option A,B and C are not the required polynomial function.
Now, we will show that the option D is the required polynomial function.
Putting x=-2,
f(x)=(x+2)(4x-3)(x-5)
f(-2)=(-2+2)(4(-2)-3)(-2-5)
= (0)(-8-3)(-7)
= 0
Then, putting x=3/4,
f(x)=(x+2)(4x-3)(x-5)
f(3/4)=((3/4)+2)(4(3/4)-3)((3/4)-5)
\(=(\frac{3+8}{4} )(\frac{12-12}{4} )(\frac{3-20}{4} )\\\\=(\frac{3+8}{4} )(0 )(\frac{3-20}{4} )\\=0\)
Then, putting x=5,
f(x)=(x+2)(4x-3)(x-5)
f(5)=(5+2)(4(5)-3)(5-5)
= (5+2)(4(5)-3)(0)
= 0
Therefore, the polynomial function has zeros when x=-2,3/4,5 is option D f(x)=(x+2)(4x-3)(x-5).
To learn more about function, visit:
brainly.com/question/5975436?referrer=searchResults
#SPJ1
5. Write a function of the form f(x) = - + k with a vertical asymptote at x = -15 and a horizontal asymptote of y = -6.
Answers
Un concensario de coches rebaja a 16000 un vehiculo que valia 18300 en que porcentaje lo han rebajado?
Answers
As a car dealer lowers a vehicle that was worth 18300 to 16000 by applying the formula of change in percentage we get that by 12.569 percentage (approximately) the price gets lowered .
The initial price of the car is set at P = 18300 (units)
The price after lowering drom P becomes A= 16000 (units)
Hence the change in price (or value) of the car, that is the price of the car is lowered by, C = (initial price - lowered price) = (P - A) = (18300 - 16000) units = 2300 units.
The formula for calculating percentage change is given as follows,
Change in percentage = [(Change in value)/ ( Initial value) ]*100
⇒Change in percentage = (C/ P)*100
⇒ Change in percentage =( 2300/ 18300)*100 = 12.569% (approximately)
To know more about change iin percentage here
https://brainly.com/question/14801224
#SPJ4
Find the 15th term of the arithmetic sequence whose common difference is d= 7 and whose first term is a1 = 5
Answers
Answer:
The 15th term is 103
Step-by-step explanation:
Arithmetic Sequence
An arithmetic sequence is a list of numbers with a definite pattern by which each term is found by adding or subtracting a fixed quantity to the previous term. If n is the number of the term, then:
\(a_n=a_{n-1}+d\)
Where d is called the common difference. If we know the first term, the nth term is calculated by:
\(a_n=a_1+(n-1)*d\)
The question asks us to find the term n=15 of an arithmetic sequence with a common difference d=7 and first term a1=5.
Applying the formula above:
\(a_{15}=5+(15-1)*7\)
\(a_{15}=5+14*7\)
\(a_{15}=5+98=103\)
The 15th term is 103
Sara invests $4000 at 7.2% annual interest compounded monthly. Find the final amount of Sara's investment after 15 years. *
Answers
Answer:
$8,711.99
Step-by-step explanation:
The formula for calculating the compound interest in expressed as;
A =P(1+r/n)^nt
Principal P = $4000
r is the rate = 7.2% = 0.072
t is the time = 15years
n = 1/12
Substitute
A = 4000(1+0.072(1/12))^15/12
A = 4000(1+0.072(12))^1.25
A = 4000(1+0.864)^1.25
A = 4000(1.864)^1.25
A = 4000(2.1779)
A = 8,711.99
Hence the final investment after 15years is $8,711.99
Acorn falls from a tree "h=98-18t^(2)" (height depends on time)
a) When "t=2 seconds," find "h"
____ft
b) Find "t" when the acorn hits the ground. (to nearest tenth)
____seconds
Answers
Using the equation h = 98 - 18t², the values are -
a) The height of acorn is obtained to be 26 feet.
b) The time when acorn hits the ground is obtained as 2.3 seconds.
What is an equation?
A mathematical definition of an equation is a claim that two expressions are equal when they are joined by the equals sign ("=").
a) When t = 2 seconds, we can find the height of the acorn by plugging in t = 2 into the equation for height -
h = 98 - 18t²
h = 98 - 18(2)²
h = 98 - 18(4)
h = 98 - 72
h = 26 feet
Therefore, when t=2 seconds, the height of the acorn is 26 feet.
b) We can find the time it takes for the acorn to hit the ground by setting h to 0 in the equation for height and solving for t -
h = 98 - 18t²
0 = 98 - 18t²
18t² = 98
t² = 98/18
t² ≈ 5.4444
t ≈ √5.4444
t ≈ 2.33 seconds (rounded to the nearest tenth)
Therefore, the acorn hits the ground after approximately 2.3 seconds.
To learn more about equation from the given link
https://brainly.com/question/28871326
#SPJ1
the vector sum of two or more other vectors is called the
Answers
Answer: resultant
Step-by-step explanation:
Find the equation of the line that passes through (1,2) and is perpendicular to y = 2 x + 3
Answers
Answer:
See belowStep-by-step explanation:
The slope of the perpendicular line with y = 2x + 3 is m = - 1/2.
Use point-slope form to find its equation:
y - y₁ = m(x - x₁)y - 2 = - 1/2(x - 1)or
y = -1/2x + 2 1/2or
y = -0.5x + 2.5Answer:
See below
Step-by-step explanation:
The slope of the perpendicular line with y = 2x + 3 is m = - 1/2.
Use point-slope form to find its equation:
y - y₁ = m(x - x₁)
y - 2 = - 1/2(x - 1)
or
y = -1/2x + 2 1/2
or
y = -0.5x + 2.5
give brainliest to me or to the person below or up bc I ctrl+c and ctrl+v
bc is soooo coool the other one lol
i also need this asap
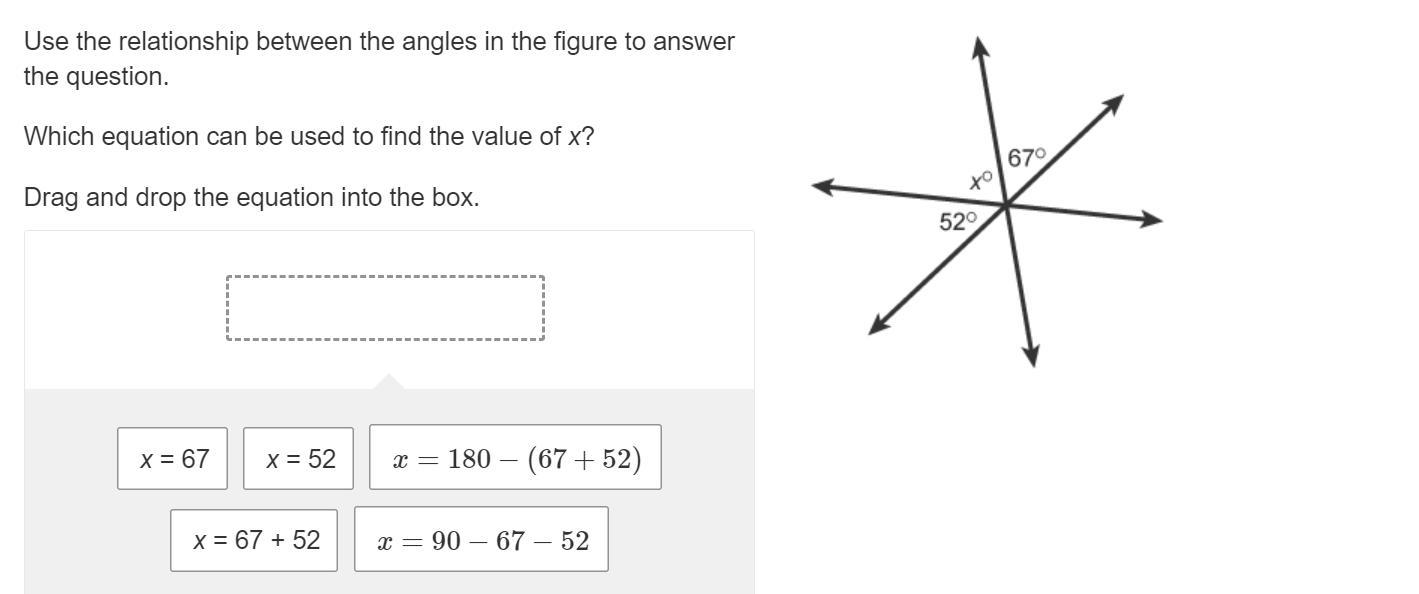
Answers
Answer:
x=180-(67+52)
Step-by-step explanation:
a linear pair is 180
we are already have two angles add them together
subtract that from 180 and you will get the last angle
The answer is in the picture. I need help ASAP!!

Answers
The perimeter of the given shape above would be = 40.56in.
How to calculate the area and perimeter of the given shape?To calculate the perimeter of the given shape, the formula for the perimeter of a rectangle and a semi circle is used.
Perimeter of rectangle =2(l+w)
where,
length = 8in
width = 6in
perimeter = 2(6+8)
= 2×14 = 28in
perimeter of semi circle ;
= 2πr/2
where;
r = 8/2 = 4 in
= 2×3.14× 4/2
= 3.14×4 = 12.56in
Perimeter of the shape = 28+12.56 = 40.56
Learn more about perimeter here:
https://brainly.com/question/31068918
#SPJ1
(2/5)^-2(-3)^4
What is the equivalent?
Answers
Answer:
-8100
Step-by-step explanation:
(2/5)^-2(-3)^4
Given data
and second term
The first term= (2/5)^-2 and
Second term=(-3)^4
Simplify the first term
(2/5)^-2= 2^-2/ 5^-2= 1/2^2 * 1/5^2
=1/4/ 1/25
=1/4*25/1
=100
Simplify the second term
=(-3)^4
= -81
Hence, 100*81
=-8100
5) find the value of x and y

Answers
Answer:
x = 45°, y= 5°
Step-by-step explanation:
x = 9y
90+2x = 180
2x = 90
x = 45
so x = 45
9y = 45
y = 5
Help please. This is a test man. I’m begging you! Is this negative, positive, or zero?

Answers
Answer:
It's a positive slope
:)
Answer:
+++++++++++++++++++++++++++++++++++++
Step-by-step explanation:
Find the solution of the following initial value problem.g'(x)= 3x(x^2 -1/3) ; g(1) = 2
Answers
According to the question we have the solution of the given differential equation initial value problem is: g(x) = (3/4)x^4 - x + 9/4 .
To solve the given initial value problem, we need to integrate both sides of the differential equation. We have:
g'(x) = 3x(x^2 - 1/3)
Integrating both sides with respect to x, we get:
g(x) = ∫[3x(x^2 - 1/3)] dx
g(x) = ∫[3x^3 - 1] dx
g(x) = (3/4)x^4 - x + C
where C is the constant of integration.
To find the value of C, we use the initial condition g(1) = 2. Substituting x = 1 and g(x) = 2 in the above equation, we get:
2 = (3/4)1^4 - 1 + C
2 = 3/4 - 1 + C
C = 9/4
Therefore, the solution of the given initial value problem is:
g(x) = (3/4)x^4 - x + 9/4
In more than 100 words, we can say that the given initial value problem is a first-order differential equation, which can be solved by integrating both sides of the equation. The resulting function is a family of solutions that contain a constant of integration. To find the specific solution that satisfies the initial condition, we use the given value of g(1) = 2 to determine the constant of integration. The resulting solution is unique and satisfies the given differential equation as well as the initial condition.
To know more about differential visit :
https://brainly.com/question/31383100
#SPJ11
what is the surface area of a cylindrical soup can with radius 3 cm and height 2 cm? round the answer to the nearest tenth of a sq. cm.]
Answers
The surface area of the cylindrical soup can is approximately 150.7 sq. cm.
To find the surface area of a cylindrical soup can, we need to add up the area of the top and bottom circles, as well as the area of the curved side.
The area of each circle is πr^2, where r is the radius. So the area of both circles is 2π(3cm)^2 = 56.5 sq. cm (rounded to the nearest tenth).
The area of the curved side is the height times the circumference of the circle, which is 2πr. So the area of the curved side is 2π(3cm)(2cm) = 37.7 sq. cm (rounded to the nearest tenth).
To find the total surface area, we just add up these three areas:
56.5 + 56.5 + 37.7 = 150.7 sq. cm (rounded to the nearest tenth).
Therefore, the surface area of the cylindrical soup can is approximately 150.7 sq. cm.
To know more about surface areas refer here :
https://brainly.com/question/29101132#
#SPJ11
Kevin divided 1/5 our inches certain number of intervals each interval was 1/40 hour long into how many intervals did Kevin divide the time
A. 45
B. 35
C. 8
D. 5
Answers
what are the factor of 25
A.2,4,6,8,10
B.5,10,15,20,25
C.1,5,5
D.3,6,9
Answers
It’s not in the answers given above
One ninety one divided by three answer math
Answers
Answer:
Step-by-step explanation:
The expression 191 divided by 3 equals 63.66666666666667 (approximately 64)
Find each function value and limit. Use - oo or [infinity]o where appropriate.
f(x)= 9x²-18x^2/8x^5 +4 (A) (-6)
(B) f(-12)
Answers
The value at function when x is (-6) is approximately 0.070 and function when x is (-12) is approximately 0.000066 for the function f(x)= 9x²-18x^2/8x^5 +4 .
(a) To find the value of f(x) at x = -6, we substitute -6 into the function:
f(-6) = 9(-6)² - 18(-6)² / (8(-6)⁵ + 4).
Simplifying the numerator and denominator:
f(-6) = 9(36) - 18(36) / (8(-6)⁵ + 4)
= 324 - 648 / (-4,608 + 4)
= -324 / -4,604
= 0.070.
Therefore, f(-6) = 0.070.
(b) To find the value of f(-12), we substitute -12 into the function:
f(-12) = 9(-12)² - 18(-12)² / (8(-12)⁵ + 4).
Simplifying the numerator and denominator:
f(-12) = 9(144) - 18(144) / (8(-12)⁵ + 4)
= 1,296 - 2,592 / (-19,660,928 + 4)
= -1,296 / -19,660,924
= 0.000066.
Therefore, f(-12) = 0.000066.
Learn more about function here : brainly.com/question/31549816
#SPJ11
Given that air is 20.93% oxygen, there is a total pressure of 760mm hg, and that the partial pressure of oxygen in the tissues of an exercising individual is 10mm hg, the partial pressure oxygen in the venous circulation of an exercising individual at sea level is approximately ________ mm hg.
Answers
The partial pressure of oxygen in the venous circulation of an exercising individual at sea level is approximately 149 mm Hg.
In the given scenario, the total atmospheric pressure is 760 mm Hg, and the partial pressure of oxygen in the tissues is 10 mm Hg. To find the partial pressure of oxygen in the venous circulation, we subtract the tissue partial pressure from the total atmospheric pressure: 760 mm Hg - 10 mm Hg = 750 mm Hg. Therefore, the partial pressure of oxygen in the venous circulation of an exercising individual at sea level is approximately 149 mm Hg (20.93% of 750 mm Hg).
It's important to note that this calculation assumes ideal conditions and simplified models. In reality, oxygen transport in the human body is a complex process influenced by factors such as gas exchange in the lungs, oxygen binding to hemoglobin, and tissue oxygen consumption. These factors can vary among individuals and under different physiological conditions.
Learn more about Circulation:
brainly.com/question/28269937
#SPJ11
A photographer shines a camera light at a particular painting forming an angle of 40° with the camera platform. If the light is 58 feet from the wall where the painting hangs, how high above the platform is the painting?
Answers
Answer:
Let y be the height above the camera platform of the painting.
tan (40degrees) = y/58
y = 58[tan(40)] = 58(0.8391) = 48.67 feet.
y = 48.67 feet
Step-by-step explanation:
WILL GIVE MANLIESTXD!! SO I WROTE THIS SONG! IT'S LIKE MY 53rd SONG. TELL ME WHAT YOU THINK. I NEED FEEDBACK. ABSOLUTELY ANYTHING.!!!! IT"S CALLED PINKY PROMISE!!
Answers
Answer:
This is absolutely amazing! I love the passion in your anger. I can tell that this was a real life experience, and if it wasn't, your songwriting abilities are at a peak. at the melody that I read it in, it sounded sort of indie pop.
Step-by-step explanation:
Incredible story, loved it.
and the "your probably with that girl" really gave Olivia Rodrigo! love it so much.
Answer:
I love it.
Step-by-step explanation:
I really like it but one thing I learned about songwriting, make sure you are putting it through eyes.
V = √3 3-x² S -√√3-√3-x²1 4-x²-y² dzdydx
Answers
The value of the given integral is: v = [(4√(3) - 5)π/3]
To evaluate the given integral, let's calculate it step by step:
First, let's integrate with respect to z from 1 to √(4 - x² - y²):
∫[1, √(4 - x² - y²)] dz = √(4 - x² - y²) - 1
Next, let's integrate the above expression with respect to y from -√(3 - x²) to √(3 - x²):
∫[-√(3 - x²), √(3 - x²)] (√(4 - x² - y²) - 1) dy
To simplify the integration, let's convert to polar coordinates:
x = r cosθ
y = r sinθ
The bounds of integration in polar coordinates will be:
r: 0 to √(3)
θ: 0 to 2π
Now, we can rewrite the integral in terms of polar coordinates:
∫[0, 2π] ∫[0, √(3)] (√(4 - r²) - 1) r dr dθ
Evaluating the inner integral with respect to r:
∫[0, 2π] [(-1/3) (4 - r²)\(^{3/2}\) - (1/2) r²] | [0, √(3)] dθ
∫[0, 2π] [(2√(3)/3) - (1/3)(4 - 3)\(^{3/2}\) - (1/2)(√(3))²] dθ
Simplifying further:
∫[0, 2π] [(2√(3)/3) - (1/3) - (3/2)] dθ
∫[0, 2π] [(2√(3)/3) - (5/6)] dθ
Now, integrating with respect to θ:
[(2√(3)/3)θ - (5/6)θ] | [0, 2π]
[(2√(3)/3)(2π) - (5/6)(2π)] - [(2√(3)/3)(0) - (5/6)(0)]
[(4√(3)/3)π - (5/3)π] = [(4√(3) - 5)π/3]
Therefore, the value of the given integral is: v = [(4√(3) - 5)π/3]
Complete Question:
Evaluate the integral:
v = ∫∫∫ [−√3, √3] [−√(3−x²), √(3−x²)] [1, √(4−x²−y²)] dz dy dx
To know more about integral, refer here:
https://brainly.com/question/31059545
#SPJ4
Determine whether the given sequence could be geometric, arithmetic, or neither. If possible, identify either the common ratio or the common difference.
9, 13, 17, 21,....
Answers
Suppose we have a neighborhood of n houses. For any two houses we pick, there is a road between them. (a) The landlord wants to cut maintenance costs by removing some of the roads. Let k be the minimum number of roads he can remove such that the neighborhood is still connected (every house can be walked to from every other house) and there are no cycles. Determine the value of k as an expression in terms of n. Then indicate how to remove the minimum number of roads from the neighborhood such that the requirements are satisfied. (b) Suppose now instead that the landlord wants to remove houses. Let ℓ be the minimum number of houses that must be removed such that the neighborhood is still connected and has no cycles. Removing a house also removes the roads it is connected to. Determine the value of ℓ as an expression in terms of n. Then indicate how to remove the minimum number of houses from the neighborhood such that the requirements are satisfied
Answers
a) ℓ is equal to the number of leaf nodes in the graph. If we have n nodes in the graph, then the maximum number of leaf nodes that we can have is n-1 (when the graph is a tree).
b) k = (n-1) - (number of connected components).
To remove the minimum number of roads from the neighborhood such that the requirements are satisfied, we need to remove bridges.
Explanation:
Part a) To begin with, it is stated that we have a neighborhood of n houses. For any two houses we pick, there is a road between them. The landlord wants to cut maintenance costs by removing some of the roads. Let k be the minimum number of roads he can remove such that the neighborhood is still connected (every house can be walked to from every other house) and there are no cycles.
To find the minimum number of roads that he can remove, such that the neighborhood is still connected and there are no cycles, let us start by finding the total number of roads required for a connected neighborhood with n houses, where every house can be walked to from every other house.
We can use the formula for the minimum number of edges required for a connected graph, which is given by (n-1).
Thus, for n houses, we need n-1 roads.
But we have n houses and for any two houses we pick, there is a road between them.
Therefore, the total number of roads in the neighborhood is greater than or equal to n-1.
Suppose the landlord removes k roads. This means that there will be multiple disconnected components and to keep the neighborhood connected, we need to add edges between these components.
Thus, k is equal to the number of edges that need to be added to get a connected graph.
Therefore,
k = (n-1) - (number of connected components).
To remove the minimum number of roads from the neighborhood such that the requirements are satisfied, we need to remove bridges. Bridges are roads which if removed, increase the number of connected components. Removing a bridge will never create a cycle. Thus, we can start by identifying bridges and then removing them.
Part b)
Suppose now instead that the landlord wants to remove houses. Let ℓ be the minimum number of houses that must be removed such that the neighborhood is still connected and has no cycles.
Removing a house also removes the roads it is connected to. Determine the value of ℓ as an expression in terms of n. Then indicate how to remove the minimum number of houses from the neighborhood such that the requirements are satisfied.
To remove the minimum number of houses from the neighborhood such that the requirements are satisfied, we can start by finding the number of nodes that we can remove while keeping the graph connected.
Let G be a connected graph with n nodes. If we remove a node v from G along with its incident edges, then the graph will be disconnected into components.
However, if v is a leaf node (a node with degree 1), then we can remove the node and its incident edge without disconnecting the graph. If G has no leaf nodes, then it must have a cycle. Removing any node from a cycle will break the cycle and create at least one leaf node.
Thus, to remove the minimum number of nodes, we need to identify the leaf nodes and remove them until no more leaf nodes are left. The minimum number of nodes that can be removed without disconnecting the graph is equal to the number of leaf nodes in the graph.
Therefore, ℓ is equal to the number of leaf nodes in the graph. If we have n nodes in the graph, then the maximum number of leaf nodes that we can have is n-1 (when the graph is a tree).
To know more about connected graph, visit:
https://brainly.com/question/31616043
#SPJ11
the outbound trip of a bus was made at 24mi/h, while the return trip was made at 30mi/h. find the one way distance fi the total running time was 4.5 hour.
Answers
With a running time of 4.5 hours and speeds of 24 mph and 30 mph, respectively, the bus covered a one-way distance of 72 miles.
With a running time of 4.5 hours and speeds of 24 mph outgoing and 30 mph inbound, the bus covered a one-way distance of 72 miles.
As the outgoing and inbound timings were equal, the computation was performed by multiplying the outbound trip's speed by the entire running time, and then dividing the result by two. Therefore, 108 miles are equal to 24 mph times 4.5 hours. The one-way distance is equal to 72 miles when you divide this result in half. When both directions' speeds are known, this calculation can be used to determine the overall distance of a round trip.
Learn more about distance here
https://brainly.com/question/28956738
#SPJ4