What is Permutations and Combinations?
Answers
Answer:
See below
Step-by-step explanation:
Permutation is to select an object then arrange it and it cares about the orders while Combination is about only selecting an object without caring the orders.
Permutation can be expressed in math as:
\(\displaystyle{_n P _r = \dfrac{n!}{(n-r)!} \ \ \ (n \geq r) }\)
where n is a number of total object and r is a number of selected object to arrange. Hence. n cannot be less than r.
Now let's see an example of permutation, suppose we have letter A, B and C. I'd like to know how many ways these words can be arranged:
Since there are 3 letters total and 3 selected letters to arrange then:
\(\displaystyle{_3 P _3 = \dfrac{3!}{(3-3)!}}\\\\\displaystyle{_3 P _3 = \dfrac{3 \times 2 \times 1}{0!}}\\\\\displaystyle{_3 P _3 = \dfrac{6}{1}}\\\\\displaystyle{_3 P _3 = 6}\)
Therefore, there are 6 ways to arrange the letters - we can also demonstrate visually:
ABC - 1
ACB - 2
BAC - 3
BCA - 4
CAB - 5
CBA - 6
Notice that if you do visually, you'll get the same answer as the calculation of permutation!
----
Combination can be expressed mathematically as:
\(\displaystyle{_n C _r = \dfrac{n!}{(n-r)!r!} = \dfrac{_n P _r}{r!} \ \ \ (n \geq r) }\)
The difference between permutation and combination is that you only find how many ways you can select object in combination. Therefore, no arrange and doesn't care about order, just ways to select.
Suppose we have same 3 letters: A, B and C. I want to find how many ways I can select these 3 letters:
Since there are 3 letters total and 3 selected letters:
\(\displaystyle{_3 C _3 = \dfrac{3!}{(3-3)!3!}}\\\\\displaystyle{_3 C _3 = \dfrac{3!}{0!3!}}\\\\\displaystyle{_3 C _3 = \dfrac{3!}{3!}}\\\\\displaystyle{_3 C _3 = 1}\)
Hence, there is only one way to select 3 letters. This makes sense because if you have 3 letters then you can only select 3 letters only one way.
Permutations and combinations have many practical applications in various fields such as statistics, Probability theory, and computer science.
Permutations and combinations are two concepts in mathematics that deal with counting and arranging elements in a set.
Permutations refer to the number of ways in which a set of objects can be arranged or ordered. In other words, permutations involve counting the number of possible ways in which a group of objects can be arranged in a particular order. For example, if we have three objects A, B, and C, the possible permutations would be ABC, ACB, BAC, BCA, CAB, and CBA. The formula for permutations is nPr = n! / (n - r)!, where n is the total number of objects and r is the number of objects being arranged.
Combinations, on the other hand, refer to the number of ways in which a subset of objects can be selected from a larger set, without regard to the order in which they are selected. In other words, combinations involve counting the number of possible subsets that can be formed from a larger set. For example, if we have three objects A, B, and C, the possible combinations would be AB, AC, and BC. The formula for combinations is nCr = n! / (r! * (n - r)!), where n is the total number of objects and r is the number of objects being selected.
The key difference between permutations and combinations is that permutations involve ordering objects, while combinations do not. Another important distinction is that in permutations, each arrangement is considered distinct, whereas in combinations, different arrangements that contain the same objects are considered identical.
Permutations and combinations have many practical applications in various fields such as statistics, probability theory, and computer science. For example, they are commonly used in solving problems related to probability, combinations of locks, and permutations of passwords. Understanding these concepts is essential in order to effectively analyze and solve problems in these fields.
To know more about Probability theory.
https://brainly.com/question/1391215
#SPJ11
Related Questions
Resolver las siguientes inecuaciones cuadráticas y presentar el conjunto solución en forma de intervalo y gráficamente. 1) X2 < 10 – 3x 2) 2x2 + 3x ≥ 2
Answers
Respuesta:
1) (-5,2)
2) \((-\infty,-2]U(\frac{1}{2},\infty)\)
Explicación paso a paso:
1)
\(x^{2}<10-3x\)
Para comenzar este problema, debemos moverlo todo al lado izquierdo de la inecuación, por lo que obtenemos:
\(x^{2}+3x-10<0\)
Ahora podemos factorizar el lado izquierdo para obtener:
\((x+5)(x-2)<0\)
Ahora podemos cambiar el símbolo < por un = para encontrar los valores de x en los cuales la inecuación es igual a cero.
(x+5)(x-2)=0
Y luego despejamos x.
x+5=0
x=-5
y
x-2=0
x=2
Ahora construimos nuestros intervalos posibles.
\((-\infty,-5)\)
(-5,2)
y
\((2,\infty)\)
Y escogemos algunos valores de prueba. Estos nos ayudarán a determinar si cada intervalo hace que la inecuación sea verdadera o falsa.
\((-\infty,-5)\)
Para este intervalo escojamos -6 y evaluemoslo en la inecuación.
(x+5)(x-2)<0
(-6+5)(-6-2)<0
(-1)(-8)<0
8<0
falso, así que este intervalo no es parte de nuestra respuesta.
(-5,2)
para este escojamos x=0 y probémoslo en la inecuación.
(x+5)(x-2)<0
(0+5)(0-2)<0
(5)(-2)<0
-10<0
verdadero, así que este intervalo es parte de nuestra respuesta.
\((2,\infty)\)
Para este escojamos 3 y probémoslo en unestra inecuación.
(x+5)(x-2)<0
(3+5)(3-2)<0
(8)(1)<0
8<0
falso, así que este intervalo no es parte de nuestra respuesta.
así que nuestra respuesta es: (-5,2)
Vea imagen adjunta para representación gráfica.
2)
\(2x^{2}+3x\geq2\)
Para resolver este problema, comenzamos moviéndolo todo al lado izquierdo de la inecuación.
\(2x^{2}+3x-2\geq0\)
Ahora podemos factorizar el lado izquierdo de la inecuación para obtener:
\((2x-1)(x+2)\geq0\)
Ahora podemos cambién el símbolo ≥ por un símbolop de = para obtener los valores de x que hacen que la inecuación sea igual a 0.
(2x-1)(x+2)=0
y ahora despejamos x.
2x-1=0
\(x=\frac{1}{2}\)
y
x+2=0
x=-2
Ahora construimos nuestros intervalos posible.
\((-\infty,-2]\)
\([-2,\frac{1}{2}]\)
y
\([\frac{1}{2},\infty)\)
Ahora escogemos los valores de prueba correspondientes.
\((-\infty,-2]\)
para este, escojamos -3 y probémoslo en la inecuación.
\((2x-1)(x+2)\geq0\)
\((2(-3)-1)(-3+2)\geq0\)
\((-7)(-1)\geq0\)
\(7\geq0\)
verdadero, así que este intervalo es parte de nuestra respuesta.
\([-2,\frac{1}{2}]\)
para este, utilicemos 0 como valor de prueba.
\((2x-1)(x+2)\geq0\)
\((2(0)-1)(0+2)\geq0\)
\((-1)(2)\geq0\)
\(-2\geq0\)
falso, así que este intervalo no es parte de nuestra respuesta.
\([\frac{1}{2},\infty)\)
para este, utilicemos 1 como valor de prueba.
\((2x-1)(x+2)\geq0\)
\((2(1)-1)(1+2)\geq0\)
\((1)(3)\geq0\)
\(3\geq0\)
verdadero, así que este intervalo es parte de nuestra respuesta.
Así que nuestra respuesta es la unión entre los dos intervalos que resultaron verdadero, por lo que nuestra respuesta es:
\((-\infty,-2]U[\frac{1}{2},\infty)\)
Vea la representación gráfica en la imagen adjunta.

In general, describe how the outcome of the hypothesis test changes as the level of significance decreases.
Answers
Answer:
The region of acceptance gets bigger and the null hypothesis is mostly accepted as it lies in the acceptance region.
Step-by-step explanation:
As the level of significance is decreased the area for the favorable outcomes is increased. The value of ∝= 0.1 has a narrower area of favorable outcomes then the values of ∝= 0.05 or 0.01 because the value 0.1 ( 1%) is closer to the middle value or at the extreme values of the distribution as the case may be for 2 tailed or 1 tailed test.
Significance level Two tailed Test One tailed test
0.1 ± 1.645 ±1.28
0.05 ±1.96 ± 1.645
0.01 ± 2.58 ± 2.33
So if the middle point is taken as zero we see that the spread of the area of the favorable values increases as the value of ∝ significance level decreases.
The region of acceptance gets bigger and the null hypothesis is mostly accepted as it lies in the acceptance region.

Which derived character is placed immediately after that group on the cladogram?
Answers
Answer:
Step-by-step explanation:
One that has the next least in common with the rest.
What is the probability that either event will occur?
Now, find the probability of event A and event B.
A
B
6
6
20
20
P(A and B) = [?]

Answers
The probability of event A and event B is 6.
Given that, P(A)=6, P(B)=20 and P(A∩B)=6.
P(A/B) Formula is given as, P(A/B) = P(A∩B) / P(B), where, P(A) is probability of event A happening, P(B) is the probability of event B.
P(A/B) = P(A∩B) / P(B) = 6/20 = 3/10
We know that, P(A and B)=P(A/B)×P(B)
= 3/10 × 20
= 3×2
= 6
Therefore, the probability of event A and event B is 6.
To learn more about the probability visit:
https://brainly.com/question/11234923.
#SPJ1
Explain why this binomial is not a difference of two squares: x^2+9
Answers
The given binomial x² + 9 as given in the task content is not a difference of two squares because the arithmetic sign between the two terms represents a sum.
Why is the binomial not a difference of two squares?By observation; although the terms x² and 9 represent perfect squares, it follows that the sign between the two terms is an addition sign.
Hence, the given binomial does not qualify to be termed the difference of two squares.
Read more on difference of two squares;
https://brainly.com/question/3189867
#SPJ1
Given a function f(x)=2x²+2/ax²+bx+c, find a,b,and c such that the point (0,-1) belongs to the cuve and line with equation x+2/3=0 and x =1 are asymptotes to the curve
Answers
The values of a, b, and c are -1/8, -1/12, and -1/2, respectively, to satisfy the conditions of the point (0, -1) belonging to the curve and the lines x + 2/3 = 0 and x = 1 being asymptotes to the curve.
To find the values of a, b, and c that satisfy the given conditions, we'll start by considering the asymptotes. The line x + 2/3 = 0 implies that x = -2/3 is a vertical asymptote. Also, x = 1 is a vertical asymptote. This means that the denominator of the function must have factors of (x + 2/3) and (x - 1) to create these asymptotes.
Using the given point (0, -1), we can substitute the values into the function to solve for a, b, and c:
f(0) = 2(0)² + 2/(a(0)² + b(0) + c) = -1
2c = -1
c = -1/2
Next, we'll consider the asymptote (x + 2/3). To make it an asymptote, the corresponding factor in the denominator should cancel out. So, (x + 2/3) should be a factor of ax² + bx. Expanding the factor (x + 2/3), we get x + 2/3 = 0, which simplifies to x = -2/3. This means that x = -2/3 is also a root of ax² + bx.
Since x = -2/3 is a root, we can substitute it into ax² + bx to find the value of a + b:
a(-2/3)² + b(-2/3) = 0
4a/9 - 2b/3 = 0
4a - 6b = 0
2a - 3b = 0
2a = 3b
Now, we have two equations:
c = -1/2
2a = 3b
We can solve this system of equations to find the values of a and b.
Substituting 2a = 3b into the equation c = -1/2:
2(3b) = -1/2
6b = -1/2
b = -1/12
Substituting the value of b into 2a = 3b:
2a = 3(-1/12)
2a = -1/4
a = -1/8
Therefore, the values of a, b, and c that satisfy the given conditions are
a = -1/8, b = -1/12, and c = -1/2.
Learn more about ”asymptotes” here:
brainly.com/question/32503997
#SPJ11
In circle I, IJ=4 and mJIK∠=90∘ Find the area of shaded sector. Express your answer as a fraction times π.
Answers
The area of the shaded sector is 4π square units.
To find the area of the shaded sector, we need to calculate the central angle formed by the sector. In this case, we are given that the angle JIK is 90 degrees, which means it forms a quarter of a full circle.
Since a full circle has 360 degrees, the central angle of the shaded sector is 90 degrees.
Next, we need to determine the radius of the circle. The line segment IJ represents the radius of the circle, and it is given as 4 units.
The formula to calculate the area of a sector is A = (θ/360) * π * r², where θ is the central angle and r is the radius of the circle.
Plugging in the values, we have A = (90/360) * π * 4².
Simplifying, A = (1/4) * π * 16.
Further simplifying, A = (1/4) * π * 16.
Canceling out the common factors, A = π * 4.
Hence, the area of the shaded sector is 4π square units.
Therefore, the area of the shaded sector, expressed as a fraction times π, is 4π/1.
In summary, the area of the shaded sector is 4π square units, or 4π/1 when expressed as a fraction times π.
For more such questions on area, click on:
https://brainly.com/question/25292087
#SPJ8
Once we have categorized an object, our memory of the object increasingly resembles thecategoryA) algorithm.B) prototype.C) heuristic.D) mental set
Answers
Once we have categorized an object, our memory of the object increasingly resembles the category is B) prototype. This means that when we categorize an object, our memory of it begins to resemble the prototype or typical example of that category. For example, if we categorize a bird as a robin, our memory of the bird will increasingly resemble the characteristics of a typical robin.
This happens because our brain uses prototypes as a shortcut to process information and make sense of the world around us. We use prototypes to quickly identify objects and make assumptions about their characteristics based on their category.
our memory of an object after categorization is influenced by the prototype of the category. This helps us to quickly process and make sense of information, but it can also lead to errors and biases in our thinking.
A prototype is a mental image or best example of a category. When we categorize an object, our memory of the object increasingly resembles the prototype because we tend to recall the most representative or typical example of the category.
Once we categorize an object, our memory of the object becomes more like the prototype, which is the best example of the category. This is because we tend to remember the most representative or typical examples of a category.
To know more about prototype, visit:
https://brainly.com/question/28187820
#SPJ11
Describe a real-world situation that can be
represented by the inequality shown in the graph.

Answers
The inequality is: y > -4x - 16
A real-world situation is the number of boys in a class is more than 4 times the number of girls.
What is inequality?
An inequality is a relationship that makes a non-equal comparison between two numbers or other mathematical expressions. It is most commonly used to compare two numbers on the number line based on their size.
The inequality is: y > 2x + 1
A real-world situation is the number of boys in a class is more than 4 times the number of girls.
The inequality
From the attached graph, we have the following points
(x₁, y₁) = (4, 16)
(x₂, y₂) = (8, 8)
Calculate the slope (m)
\(m =\frac{y_{2} - y_{1} }{x_{2} - x_{1} }\)
then,
m = 8-16 /8-4
m = -4
So, the inequality is:
y > m(x - x₁) + y₂
y > -4(x - 4) + 8
y > -4x + 16 - 32
y > -4x - 16
The inequality is y > -4x - 16 and a real-world situation is:
The number of boys in a class is more than 4 times the number of girls.
The number of boys would be on the y-axis, while the number of girls would be on the x-axis.
To learn more about inequality visit:
https://brainly.com/question/24372553
#SPJ1
If y varies directly with x and y=4 and y=12. Find the direct variation equation (find k and put into an equation).
Answers
Answer:
When in public, wear a mask
Just a teeny, weeny task
It helps keep is safe and sound
Health and care, all around
On your mouth, and on your nose
Good to cover both of those
Step-by-step explanation:
It's called the mask song you can ask Google assistant to sing it for you:)
Solve for c round your answer to the nearest tenth

Answers
Answer:
C = 7.72 ~ 7.7
Step-by-step explanation:
So when you solve this equetion you must 1st find x then c
we can find x by using cos(60)
cos(60) = x/14
x = cos(60) × 14
x = 1/2 ×14
x = 7
so after we find x we are going to solve c by using cos (25)
cos (25) = X/C = 7/c
cos(25) × C = 7
C = 7/cos (25)
C = 7.72 ~ 7.7
so the solution is 7.7

Part 1: Explain what the following variables represent and how changing each one affects the monthly payment amount: P, i, and t.
Part 2: Explain how changing each variable (P, i, and t) affects the total cost of principal and interest over the life of the loan.
Answers
Answer:
Part 1 and 2: P represents principle, or the original cost of the mortgage. i represents the annualinterest rate (r/n), and t represents time. When you change the time it affects monthlypayments because theres either more or less time to pay off the mortgage. Having a longertime to pay off means you'll have lower monthly payments. When the interest rateincreases, the monthly payment increases. This is because the higher the interest rate, themore interest you're paying. Changing the principle means you either have more or lessmoney to pay off.P2: Increasing i will increase the total cost since more interest will be charged. Increasingtime means there's more periods for interest to gather so the total cost will increase.Shortening the time will decrease the total cost because there will be less time for interestto accumulate.
in a survey of patients in a local hospital, 62.42% of the respondents indicated that the health care providers needed to spend more time with each patient. who makes up the population? a. hospital patients b. all survey respondents c. all patients in a local hospital d. cannot be determined from the information given.
Answers
The option (c) all patients in a local hospital makes up the population
Surveys are a commonly used method for collecting data in various fields, including healthcare. They can provide valuable insights into patients' experiences, opinions, and preferences, which can help healthcare providers improve their services.
In this case, the survey was conducted among patients in a local hospital, and the results showed that 62.42% of the respondents believed that healthcare providers needed to spend more time with each patient.
The answer is not immediately obvious, but we can make some inferences based on the information given. However, we cannot generalize the results to all patients in the area or the entire population.
Third, surveys cannot account for all the factors that may influence the results, such as demographic characteristics, health status, or cultural background.
Therefore, we can conclude that the population under study is "patients in a local hospital" who participated in the survey.
To know more about survey here.
https://brainly.com/question/13532910
#SPJ4
Please help meeeeeeeeeee !!!!!!!!!!!!!!!!

Answers
There are 7 ounces of applesauce in each container
What is an equation?An equation consists of numbers and variables linked together by mathematical operations to form an expression.
Let x represent the quantity of Newton applesauce
Descartes makes 72.5 ounces of applesauce, which is 2.5 times of Newtons, hence:
2.5x = 72.5
x = 29 ounce
Newton eats 8 ounces, hence:
Remaining = 29 - 8 = 21 ounces
The remaining is placed into 3 containers. If y represent the amount per container:
3y = 21
y = 7 ounces
There are 7 ounces in each container
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
how would you answer 8 (4 + 2) im confused please help
Answers
Residents of the town of Maple Grove who are connected to municipal water supply are billed a fixed amount yearly plus a charge for each cubic foot of water used. A household using 1000 cubic feet was billed $90, while one using 1600 cubic feet was billed $105. What is the charge per cubic foot? How do you wite an equation for the total cost of a residen'ts water as a function of cubic feet of water used? How many cubic feet of water used would lead to a bill of $130. I am lost from the beginning of how to start this problem.
Answers
The charge per cubic foot is $0.05. The equation for the total cost of a resident's water is C(x) = 0.05x + 40. The number of cubic feet of water used that would lead to a bill of $130 is 2200.
We will use the given data to calculate the charge per cubic foot:Let x be the number of cubic feet of water used by a household and let y be the corresponding bill amount.
Case 1: When a household using 1000 cubic feet was billed $90.
Case 2: When one using 1600 cubic feet was billed $105.Subtracting case 1 from case 2, we get:$$105 - 90 = 15$$$$1600 - 1000 = 600$$So, the charge per cubic foot is:$$\frac{15}{600} = 0.025$$$$\implies 0.05 \text{ (for two decimal place)}$$ Hence, the charge per cubic foot is $0.05.
To write an equation for the total cost of a resident's water as a function of cubic feet of water used, we will use the given data:
$$\text{Fixed amount = } $40$$\text{Charge per cubic foot of water used = } $0.05$$\text{Number of cubic feet used = } x$$
Therefore, the equation for the total cost of a resident's water as a function of cubic feet of water used is:
$$C(x) = \text{(Charge per cubic foot of water used)}\times\text{(Number of cubic feet used)}+\text{(Fixed amount)}$$$$C(x) = 0.05x + 40$$
To find out how many cubic feet of water used would lead to a bill of $130, we will use the equation obtained above:
$$C(x) = 0.05x + 40
= $130$$$$\implies 0.05x
= $90$$$$\implies x
= \frac{90}{0.05}
= 1800$$
Therefore, the number of cubic feet of water used that would lead to a bill of $130 is 1800.
To know more about resident's water, visit
https://brainly.com/question/30332520
#SPJ11
Identify the perimeter and area of an equilateral triangle with height 12 cm. Give your answer in simplest radical form.
Answers
Answer:
perimeter is 36 cm
Step-by-step explanation:
I need help with this please because I don’t know how to do it and I never learned it before.

Answers
Answer:
3ft to 1ft
Step-by-step explanation:
24/8=3 and 8/8=1
Imagine that r1 is a well-founded relation on a and r2 is a well-founded relation on b. Prove that the lexicographic ordering on pairs ( a,b) is well-founded. The lexicographic ordering says that the pair ( x
−
1, y
−
1 ) is below the pair (x_2, y
−
2 ) if either - r1×1×2, or - x1=x2 and r2y1y2 You should first define the lexicographic ordering and then prove well-foundedness.
Answers
The lexicographic ordering on pairs (a,b) is well-founded, assuming that r1 is a well-founded relation on a, and r2 is a well-founded relation on b. The lexicographic ordering is defined as the pair (x1, y1) is less than the pair (x2, y2) if either x1 < x2, or (x1 = x2 and y1 < y2).
Now let's prove it is well-founded:
Let (a1, b1), (a2, b2),... be an infinite sequence of pairs of elements. Since r1 is well-founded, there exists an a such that (a, a1), (a, a2),... is a r1-chain.
Then since r2 is well-founded, there must exist a pair (a, bj) that is minimal with respect to r2.Now we have two cases:
Case 1:
For some i, (ai, bi) is less than (a, bj).
Then, we have that (a1, b1), (a2, b2),... (ai−1, bi−1), (a, bj), (ai+1, bi+1),... is a well-ordering chain of pairs of elements under the lexicographic ordering.
Case 2:
(ai, bi) is greater than or equal to (a, bj) for all i.In this case, we have that (a, bj) is a minimal element in the infinite sequence of pairs of elements under the lexicographic ordering.
Hence, the lexicographic ordering is well-founded.
Learn more about lexicographic from the given link
https://brainly.com/question/31311785
#SPJ11
Which of the following represents z equals negative 5 radical 3 end radical minus 5 times i in trigonometric form?

Answers
SOLUTIONS
This is the trigonometric form of a complex number where
\(z=-5\sqrt{3}-5i\)
the modulus and
θ
is the angle created on the complex plane.
From the graph, a = r cos θ and b = r sin θ.
z=a+bi
z=rcosθ+irsinθ
z=r(cosθ+isinθ)
\(\begin{gathered} r=\sqrt{a^2+b^2} \\ r=\sqrt{5\sqrt{3})^2+5^2} \\ r=\sqrt{75+25} \\ r=\sqrt{100} \\ r=10 \end{gathered}\)Trigonometric Form of a Complex Number
z=r(cosθ+isinθ)
r is called the modulus and θ is called the argument
Convert between trigonometric form and standard form using
a=rcosθ
b=rsinθ
tanθ=b/a
\(\begin{gathered} tan\theta=\frac{b}{a}=\frac{-5}{-5\sqrt{3}}=\frac{1}{\sqrt{3}} \\ \theta=tan^{-1}(\frac{1}{\sqrt{3}}) \\ \theta=210 \end{gathered}\)Therefore the trigonometric form will be
\(\)At LaGuardia Airport for a certain nightly flight, the probability that it will rain is 0.11 and the probability that the flight will be delayed is 0.14. The probability that it will not rain and the flight will leave on time is 0.76. What is the probability that the flight would be delayed when it is raining? Round your answer to the nearest thousandth.
Answers
Since probabilities cannot be negative, we can conclude that the given probabilities are inconsistent or there might be an error in the information provided. Please verify the values and provide correct probabilities so that we can accurately calculate P(B|A), the probability of the flight being delayed when it is raining.
Let's denote the events as follows:
A: It will rain
B: The flight will be delayed
We are given the following probabilities:
P(A) = 0.11 (probability of rain)
P(B) = 0.14 (probability of flight delay)
P(A'∩B') = 0.76 (probability of no rain and on-time departure)
We can use the probability formula to calculate the probability of the flight being delayed when it is raining, P(B|A), which is the probability of B given A.
We know that:
P(B|A) = P(A∩B) / P(A)
To find P(A∩B), we can use the formula:
P(A∩B) = P(A) - P(A'∩B')
Substituting the given values:
P(A∩B) = P(A) - P(A'∩B')
P(A∩B) = 0.11 - 0.76
P(A∩B) = -0.65
for similar questions on probability.
https://brainly.com/question/251701
#SPJ8
In quantitative research, data collection from the same respondents at 2 or more points (waves) in time is referring to?
Answers
In quantitative research, data collection from the same respondents at 2 or more points (waves) in time is referring to "longitudinal."
What is quantitative research?A method for gathering and interpreting numerical data is known as quantitative research. It can be used to discover patterns and averages, to make predictions, to verify causal linkages, and to generalize results to larger groups.
Some features regarding quantitative research are-
The antithesis of qualitative research, that involves collecting and interpreting non-numerical data, is quantitative research (like, text, video and audio).Quantitative research is utilized extensively in the scientific and social sciences, including biology, psychology, economics, chemistry,sociology, and marketing.Experimental and correlational research are both used to statistically test hypotheses or predictions. Based on the sample method utilized, the findings may be applied to larger populations.For collect quantitative data, procedures that translate abstract notions (e.g., mood) into measurable and quantifiable metrics are frequently required.To know more about quantitative research, here
https://brainly.com/question/7705888
#SPJ4
18 A student has 273 matchsticks with which to make a pattern of nested triangles. Fig. 18.9 shows the first three triangles. Fig. 18.9 If all the matchsticks are used, how many matchsticks will each side of the biggest triangle contain? 18 A student has 273 matchsticks with which to make a pattern of nested triangles . Fig . 18.9 shows the first three triangles . Fig . 18.9 If all the matchsticks are used , how many matchsticks will each side of the biggest triangle contain ?
Answers
The number of matchsticks that each side of the biggest triangle contains is; 137 matchsticks
How to find the biggest side of a triangle?We know that for a diagram to be a triangle, then two smallest sides must not be greater than the third side.
Now, if there are 273 matchsticks, then the greatest side of the triangle must not be less than 273/2 = 136.5 ≈ 137
Thus, the largest side will have at least 137 matchsticks
Read more about Biggest Triangle at; https://brainly.com/question/7620723
#SPJ1

Choose the letter corresponding to the best answer.
Which is a true statement?
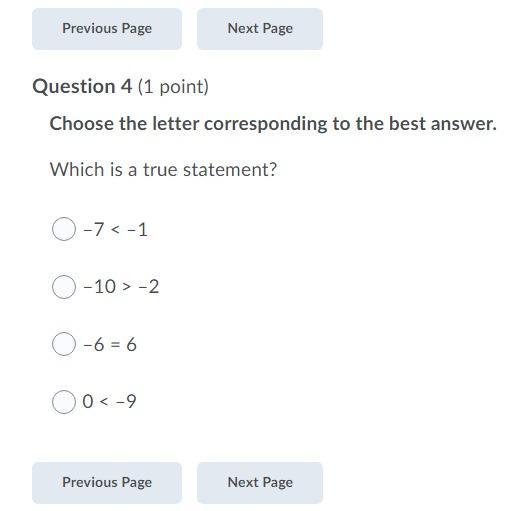
Answers
1.1 Study: Rational and Irrational Numbers
entify each number as rational or irrational.
Number
4 1/3
8
√13
Type
Irration number
Rational number
ocitet..
Answers
Irrational numbers are real numbers that can't be expressed as a fraction, p/q, where p and q are integers.
The numerator q does not equal zero (q≠ 0). Furthermore, an irrational number's decimal expansion is neither terminating nor repeating.Irrational numbers are all square roots that are not a perfect square. {√2, √3, √5, √8}Some well-known irrational numbers include Euler's number, the Golden ratio, and Pi. {e, ∅, ㄫ}Any prime number's square root is an irrational number.Thus, √13 is irrational number.
Rational numbers are written in the form p/q, where p and q can be any integer as well as q≠ 0 respectively. Natural numbers, whole numbers, integers, fractions of integers, and decimals are all examples of rational numbers.Integers such as -2, 0, 3, and so on are rational numbers.Rational numbers are fractions with integer numerators and denominators, such as 3/7, -6/5, and so on.Thus, 4 1/3 and 8 are rational number.
To know more about Rational and Irrational Numbers, here
https://brainly.com/question/5796983
#SPJ13
Given the demand function,
Q=54−5P+4PA+0.1Y,
where Q is the quantity of chocolate demanded, P is the price of chocolate, PA is the price of an apple and Y is income, find:
(i) the own price elasticity of demand for chocolate
(ii) the cross price elasticity of demand (
iii) the income elasticity of demand where P=3,PA =2 and Y=100. Comment on the economic significance of your answers.
Answers
The income elasticity of demand is positive, implying that chocolate is a normal good = 0.037
The demand function, Q = 54−5P + 4PA + 0.1Y.
Where Q is the quantity of chocolate demanded, P is the price of chocolate, PA is the price of an apple, and Y is income.
(i) The own-price elasticity of demand for chocolate, we first need to find the expression for it.
The own-price elasticity of demand can be expressed as:
Own-price elasticity of demand = (Percentage change in quantity demanded) / (Percentage change in price)Or,E
P = (ΔQ / Q) / (ΔP / P)E P = dQ / dP * P / Q
Let's calculate the own-price elasticity of demand:
EP= dQ / dP * P / Q= (-5) / (54 - 5P + 4PA + 0.1Y) * 3 / 30
= -0.1667
So, the own-price elasticity of demand for chocolate is -0.1667.
(ii) The cross-price elasticity of demand, we must first determine the expression for it.
The cross-price elasticity of demand can be expressed as:
Cross-price elasticity of demand
= (Percentage change in quantity demanded of chocolate) / (Percentage change in price of apples) Or, E
PA = (ΔQ / Q) / (ΔPA / PA)E PA = dQ / dPA * PA / Q
Let's calculate the cross-price elasticity of demand:
EP = dQ / dPA * PA / Q= (4) / (54 - 5P + 4PA + 0.1Y) * 2 / 30= 0.0296
So, the cross-price elasticity of demand is 0.0296.
(iii) The income elasticity of demand can be expressed as:
Income elasticity of demand = (Percentage change in quantity demanded) / (Percentage change in income)Or,E
Y = (ΔQ / Q) / (ΔY / Y)E Y = dQ / dY * Y / Q
Let's calculate the income elasticity of demand: EY = dQ / dY * Y / Q= (0.1) / (54 - 5P + 4PA + 0.1Y) * 100 / 30
= 0.037
The own-price elasticity of demand is negative, meaning that the quantity demanded of chocolate decreases when the price of chocolate increases.
The cross-price elasticity of demand is positive, indicating that chocolate and apples are substitute goods.
For more related questions on income elasticity:
https://brainly.com/question/29564308
#SPJ8
Which of the following are prime factorizations of the number 100? Check all
that apply.
A. 5, 2, 2,5
B. 2, 5, 10
C. 5, 10, 2
D. 5, 2, 5, 2
Answers
Answer:
Step-by-step explanation:
A. 5, 2, 2, 5 is a prime factorization of 100 since 5 and 2 are prime factors of 100 and multiplying them gives 100.
B. 2, 5, 10 is not a prime factorization of 100 since 10 is not a prime factor of 100.
C. 5, 10, 2 is not a prime factorization of 100 since 10 is not a prime factor of 100.
D. 5, 2, 5, 2 is not a prime factorization of 100 since it can be simplified as 5x2x5x2 = 100, but it is not a unique prime factorization.
Therefore, the correct answer is A. 5, 2, 2, 5.
Write a program that declares two arrays of integers with the following values: one =15,3,5,87,22,56,11,6,9,26,43,12
two =2,3,54,66,98,56,10,4,9,43,33,12
Write a function match which takes 2 integer arrays (named one and two) and returns the number of times "matches" occur in parallel positions in the two arrays. That is, count the number of times one[i] ==two[i]. The size of both arrays is the same. The arrays are passed as parameters along with their size. sample Run: The two arrays have 4 matches
Answers
Here is a program that declares two arrays of integers with the given values and a function match which takes two integer arrays (one and two) and returns the number of times "matches" occur in parallel positions in the two arrays.
The size of both arrays is the same.
The arrays are passed as parameters along with their size.
Program#include
#define SIZE 12
int match(int one[], int two[], int size);
int main()
{
int one[SIZE] = {15, 3, 5, 87, 22, 56, 11, 6, 9, 26, 43, 12};
int two[SIZE] = {2, 3, 54, 66, 98, 56, 10, 4, 9, 43, 33, 12};
int matches = match(one, two, SIZE);
printf("The two arrays have %d matches\n", matches);
return 0;
}
int match(int one[], int two[], int size)
{
int count = 0;
for (int i = 0; i < size; i++) {
if (one[i] == two[i]) {
count++;
}
}
return count;
}
Output
The two arrays have 4 matches
Explanation
The program first declares two integer arrays, one[] and two[], with the given values.
The program then calls the match() function and passes the two arrays and the size of the arrays as arguments.
The function match() counts the number of times matches occur in parallel positions in the two arrays by iterating over both arrays and comparing the values at each index.
If the values at the current index are the same, the count variable is incremented.
The function then returns the count.
Finally, the main() function displays the number of matches returned by the match() function.
To know more about program, visit:
https://brainly.com/question/30613605
#SPJ11
Suppose the company wants to improve its capability to a 5-sigma level by reducing the variability of its process. Which of the following standard deviations would meet a 5-sigma capablity for Cpk? Check all that apply, and assume the process mean remains unchanged from the original problem. a. 0.005 b. 0.015 c. 0. 025 d. 0.035 e. 0.045 f. 0.055
Answers
The standard deviations that would meet a 5-sigma capability for Cpk are 0.005, 0.015, and 0.025. (Options A, B and C).
How to Determine the Standard Deviation?To determine which standard deviations would meet a 5-sigma capability for Cpk, we need to use the following formula:
Cpk = minimum((USL - mean) / 3sigma, (mean - LSL) / 3sigma)
where USL is the upper specification limit, LSL is the lower specification limit, mean is the process mean, and sigma is the process standard deviation.
For a 5-sigma capability, we want Cpk to be at least 2.0, so we can set up the following inequality:
2.0 <= minimum((USL - mean) / 3sigma, (mean - LSL) / 3sigma)
Assuming the process mean remains unchanged, and the specification limits are at ±3 sigma from the mean (which is a common assumption), we can simplify the inequality to:
2.0 <= 1/3sigma
which can be rearranged as:
sigma <= 1/6
Therefore, the standard deviation should be less than or equal to 0.1667 to achieve a 5-sigma capability.
Now we can check which of the given standard deviations meet this criterion:
a. 0.005: Yes, this is less than 0.1667.
b. 0.015: Yes, this is less than 0.1667.
c. 0.025: Yes, this is less than 0.1667.
d. 0.035: No, this is greater than 0.1667.
e. 0.045: No, this is greater than 0.1667.
f. 0.055: No, this is greater than 0.1667.
Learn more about standard deviation here: https://brainly.com/question/28225633
#SPJ1
the side elevation of a storage building is mapped on a coordinate grid. which equation could be used to determine the corresponding x value(s) of the roof line when y=8.3?

Answers
Answer:
The correct option is;
\(8.3 = -0.5 \times \left | x -5 \right | + 9\)
Step-by-step explanation:
The coordinates of the roof are;
Starting point, = (1, 7)
Maximum height = (5, 9)
Maximum range = (9, 7)
The slope of the left portion of the roof = (9 - 7)/(5 - 1) = 0.5
The equation of the left portion of the roof is given as follows;
y - 9 = 0.5 × (x - 5)
y = 0.5 × (x - 5) + 9
The slope of the right portion of the roof = (7 - 9)/(9 - 5) = -0.5
The equation of the right portion of the roof is given as follows;
y - 9 = -0.5 × (x - 5)
y = -0.5 × (x - 5) + 9
However, when x < 5, we have;
\(0.5 \times \left | x -5 \right |= -0.5 \times \left | x -5 \right |\)
\(\therefore y = 0.5 \times \left | x -5 \right | + 9 = -0.5 \times \left | x -5 \right | + 9 = 0.5 \times \left ( x -5 \right ) + 9\)
When x > 5, we have;
\(0.5 \times \left | x -5 \right |> -0.5 \times \left | x -5 \right |\)
\(\therefore y = -0.5 \times \left | x -5 \right | + 9 = -0.5 \times \left ( x -5 \right ) + 9\)
Therefore, the equation that applies to both the left and right portion of the roof is \(y = -0.5 \times \left | x -5 \right | + 9\)
Which gives the correct option as follows;
\(y = 8.3 = -0.5 \times \left | x -5 \right | + 9\)