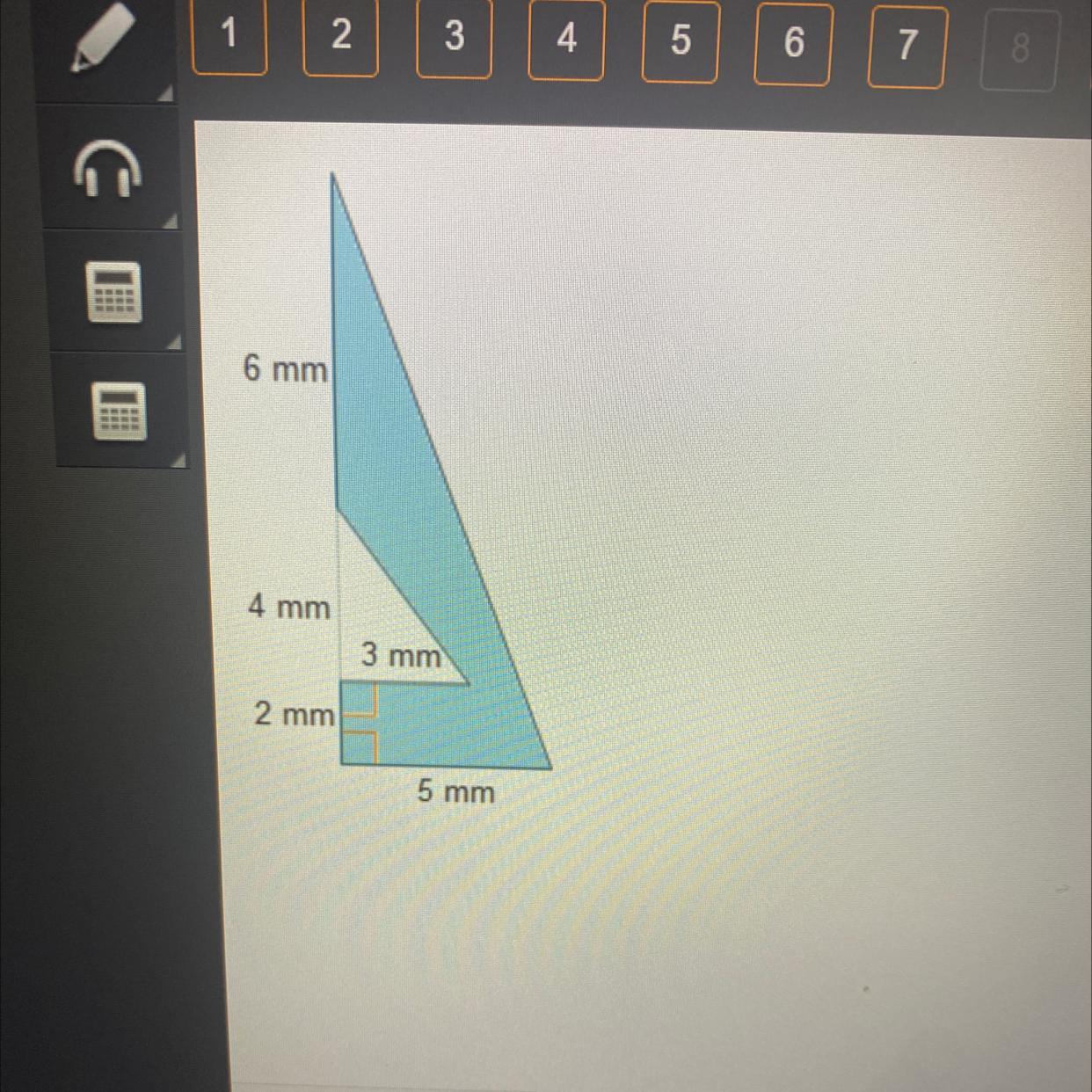
Answers
Reasoning:
The area of the big triangle will be: (6+4+2)(5)(0.5). The answer will be equal to 30 mm^2. The area of the smaller triangle will be: (4)(3)(0.5). The answer will be 6 mm^2. Next, subtract the area of the larger triangle by the smaller triangle (30-6). The final answer will then be 24mm^2.
Sorry if this may have been confusing. I had to do this on my phone.
Related Questions
Halp me this question

Answers
Answer:
15
Step-by-step explanation:
if 17-x=2
then subtract 17-2
you get 15
Answer:
?=15
Step-by-step explanation: so if we have 17-?=2 we would first do 17-2, which equals 15, then plug it back into the equation to check.
So 17-15=2
Hope that helps :)
Given circle E with diameter ‾ CD and radius ‾ EA . AB is tangent to E at A. If CD=28, solve for AC. Round your answer to the nearest tenth if necessary. If the answer cannot be determined, click "Cannot be determined."
Answers
The answer of the given question based on the circle the answer is given as AC ≈ 39.6.
What is Radius?Radius is straight line segment that joins the center of circle to any point on its circumference. It is also equal to half diameter of circle.
Since AB is tangent to circle E at point A, we know that ∠EAB = 90 degrees, and thus triangle AEB is a right triangle.
Let x be the length of AC. Then, AE = x/2 (since AE is the radius of circle E), and EB = AB - AE = x/2 - x = -x/2.
By the Pythagorean theorem applied to triangle AEB, we have:
AB² = AE² + EB²
28² = (x/2)² + (-x/2)²
784 = x²/4 + x²/4
784 = x²/2
x² = 1568
x ≈ 39.6
Therefore, AC ≈ 39.6.
To know more about Pythagorean theorem visit:
https://brainly.com/question/14930619
#SPJ1
Rewrite the equation in Ax+BY =C form please and thank you

Answers
Answer:
3x - y = 20
a = 3, b = -1, and c = 20
Step-by-step explanation:
y + 2 = 3(x - 6) => y + 2 = 3x - 18 => 3x - y = 20
how do you graph 2x-5y=20 ??
Answers

Answer:
gooogllleeeeeeeeeeeeeeee!
Step-by-step explanation:
PLEASE HELP IT IS TIMED I AM SO COMFUSED
Answers
Answer:
2 + 6 = 8. So Brendon gets 3 x (36/8)
13.5???
Step-by-step explanation:
the velocity of a body is increases from 10 m/s ti 15 m/s in 5seconds calculate its acceleration
Answers
Answer:
\(accelaration = \frac{change \: in \: veloity}{time} \\ = \frac{15 - 10}{5} \\ = \frac{5}{5} \\ = 1 \frac{m}{ {s}^{ - 2} } \)
Answer: acceleration = 1 m/s²
Concept:
Here, we need to know how to calculate the acceleration of a body.
a = Δv / Δt = (v₂ - v₁) / (t₂ - t₁)
v = velocity
t = time
unit = m/s²
Solve:
Given information
v₁ = 10 m/s
v₂ = 15 m/s
Δt = 5 seconds
Given expression
a = (v₂ - v₁) / (t₂ - t₁)
Substitute values into the expression
a = (15 - 10) / 5
Simplify values in parentheses
a = 5 / 5
Simplify by division
\(\boxed{a=1}\)
Hope this helps!! :)
Please let me know if you have any questions
Liam bought a plant and planted it in a pot near a window in his house. Let H represent the height of the plant, in inches, t months since Liam bought the plant. A graph of H is shown below. Write an equation for H then state the y-intercept of the graph and determine its interpretation in the context of the problem.

Answers
The equation of the function is: H = 4t + 10.
The y-intercept of the function is 10, which is the height of the plant when Liam initially bought it.
How to Write the Equation of a Function?To write the equation of a function, first, find the slope (m) = rise / run. You can pick any two points on the line to find the slope. Next, find the y-intercept (b) which is the point where the line intercepts the vertical axis of the graph.
Find the slope using the two points from the given graph, (5, 30) and (10, 50):
Slope (m) = change in H / change in t = (50 - 30) / (10 - 5) = 20/5
m = 4
The y-intercept is b = 10 [in this context, it is the height of the plant when Liam initially bought it]
To write the equation of the function, substitute m = 4 and b = 10 into H = mt + b:
H = 4t + 10
Learn more about the equation of a function on:
https://brainly.com/question/25638609
#SPJ1
Find the equation of the line that passes through (1,4) and is parallel to 3x + y - 1 = 0. Leave your answer in the form y = mx + c.
Answers
Answer: y=3x+1
Step-by-step explanation:
3x+y-1=0
3x+y-1+1=0+1
3x+y=1
3x-3x+y=1-3x
y=3x-1
When lines are parallel they have the same slope.
y=3x+b
4=3(1)+b
4=3+b
4-3=3-3+b
1=b
The formula is y=3x+1
a park is in the shape of a regular hexagon 22 km on a side. starting at a corner, alice walks along the perimeter of the park for a distance of 55 km. how many kilometers is she from her starting point?
Answers
Alice is 55 km from her starting point after walking a distance of 55 km along the perimeter of the park.
To find the distance Alice is from her starting point after walking along the perimeter of the park, we can use the concept of congruent sides in a regular hexagon.
The perimeter of a regular hexagon is equal to the sum of its six congruent sides. Given that each side of the hexagon is 22 km long, the total perimeter of the hexagon is 6 * 22 km = 132 km.
Since Alice walks a distance of 55 km along the perimeter of the park, we can determine the number of complete laps she makes around the hexagon by dividing the distance she walked by the perimeter of the hexagon: 55 km / 132 km = 0.4167 laps.
As Alice starts and ends at a corner of the hexagon, each complete lap brings her back to the same corner. Therefore, the fractional part of the number of laps represents the portion of the hexagon's perimeter she has traveled beyond the starting corner.
To find the remaining distance from Alice's current position to the starting point, we calculate the fractional part of the number of laps and multiply it by the perimeter of the hexagon: 0.4167 * 132 km = 55 km.
A regular hexagon is a polygon with six congruent sides. In this problem, the regular hexagon represents the shape of the park, and each side of the hexagon has a length of 22 km. The perimeter of the hexagon is found by multiplying the length of one side by the number of sides, which is 6. Therefore, the perimeter of the hexagon is 6 * 22 km = 132 km.
When Alice walks along the perimeter of the park for a distance of 55 km, we need to determine how many complete laps she makes around the hexagon. By dividing the distance she walked by the perimeter of the hexagon, we find that she completes approximately 0.4167 laps.
Since Alice starts and ends at a corner of the hexagon, each complete lap brings her back to the same corner. Therefore, the fractional part of the number of laps represents the portion of the hexagon's perimeter she has traveled beyond the starting corner.
In this case, multiplying 0.4167 by 132 km gives us a result of approximately 55 km. Therefore, Alice is 55 km from her starting point after walking a distance of 55 km along the perimeter of the park.
Learn more about perimeter here:
https://brainly.com/question/7486523
#SPJ11
when three or more lines intersect at a common point, the lines are called
Answers
Concurrent line segments are those that cross at least three other line segments at the same location.
What is concurrent lines?Concurrent line segments are those that cross at least three other line segments at the same location. In geometry, if two lines intersect at a single point in a plane or higher-dimensional space, they are said to be concurrent. In contrast to parallel lines, they exist. Concurrent lines are those that cross more than one line at the same time through a single point in a plane. The point of concurrency is a location that each of those lines shares. Triangles provide another example where this concurrency characteristic can be observed.
Here,
Concurrent line segments are those where three or more line segments cross each other at the same location.
To know more about concurrent lines,
https://brainly.com/question/23843106
#SPJ4
Now change matrix B to a 3 x 3 matrix and enter these values for B:
B =
1.2 1.4 3.1
2.2 1.1 5.6
3.7 4.2 6.7
Then select A • B to calculate the product:
77 39 −33
1.2 1.4 3.1
2.2 1.1 5.6
3.7 4.2 6.7
=
c11 c12 c13
c11 =
c12 =
c13 =
Answers
Answer:
Step-by-step explanation:
56.1,12.1,23.6
Replace m with a whole number to make the statement true. 4(m + 3) = 36
Answers
Answer:
m = 9
Step-by-step explanation:
9 + 3 is 12.
12 x 4 is 36.
find the volume of the solid whose base is bounded by x^2 y^2=4 with semicircle cross sections taken perpendicular to the x-axis.
Answers
The volume of the solid is equal to V = π∫ab22dx.
To find the volume of the solid whose base is bounded by the equation x2 + y2 = 4 with semicircle cross sections taken perpendicular to the x-axis, use the formula V = π∫abr2dx, where 'r' is the radius of the semicircle cross sections.
Since the equation of the base is bounded by x2 + y2 = 4, the radius of the semicircle cross sections is equal to r = 2.
Therefore, the volume of the solid is equal to V = π∫ab22dx.
Learn more about Volume
brainly.com/question/1578538
#SPJ11
Use Traces To Sketch The Surface. 3x^2 - 12y^2 + Z^2 = 12 Identify The Surface. Parabolic Cylinder Hyperbolic Paraboloid Elliptic
Answers
Therefore, the surface defined by the equation 3x^2 - 12y^2 + z^2 = 12 is a combination of a parabolic cylinder, a pair of hyperbolic paraboloids, and an elliptic cross-section.
The given equation 3x^2 - 12y^2 + z^2 = 12 can be rewritten as:
z^2 = 12 - 3x^2 + 12y^2
Taking the square root of both sides, we get:
z = ±sqrt(12 - 3x^2 + 12y^2)
To sketch the surface, we can take different values of x and y and plot the corresponding z values. However, it is easier to use traces.
If we set x = 0, we get:
z = ±sqrt(12 + 12y^2)
This is a pair of hyperbolic paraboloids opening up and down, one for the positive square root and one for the negative square root.
If we set y = 0, we get:
z^2 = 12 - 3x^2
This is a parabolic cylinder that opens along the x-axis.
Finally, if we set z = 0, we get:
3x^2 - 12y^2 = 12
Dividing both sides by 12, we get:
x^2/4 - y^2/1 = 1
This is the equation of an ellipse centered at the origin with semi-major axis of length 2 along the x-axis and semi-minor axis of length 1 along the y-axis.
To know more about parabolic cylinder,
https://brainly.com/question/10992563
#SPJ11
Rafael has a bag of marbles, there are 5 green marbles, 6 red marbles, and 4
5
white marbles. Rafael picks a marble out of the bag without looking. What is the
probability of P(red n white)?
Answers
The probability of getting red marble from the consider withdrawal of a marble is 0.107 approximately.
How to calculate the probability of an event?Suppose that there are finite elementary events in the sample space of the considered experiment, and all are equally likely.
Then, suppose we want to find the probability of an event E.
Then, its probability is given as
\(P(E) = \dfrac{\text{Number of favorable cases}}{\text{Number of total cases}} = \dfrac{n(E)}{n(S)}\)
where favorable cases are those elementary events who belong to E, and total cases are the size of the sample space.
Given that:
The bag contains:
5 green marbles,6 red marbles,45 white marbles.Rafael draws one marble at randomSince he draws one marbel, thus, only one colored marble would come out.
Let we suppose we've to find P(red marble coming out).
Then, if we take:
E = event of Rafael drawing a red marble,
then E can be done in 6 ways as there are 6 red marbles to choose from.
Also, withdrawal of 1 marble (of any color) can be done in (5+6+45 = 56) 56 ways.
Thus, we get:
\(P(E) = P(\text{Choosing a red marble}) = \dfrac{6}{56} = \dfrac{3}{28} \approx 0.107\)
Thus, the probability of getting red marble from the consider withdrawal of a marble is 0.107 approximately.
Learn more about probability here:
brainly.com/question/1210781
#SPJ1
Which three ratios are used to mathematically produce the return on equity ratio.
Answers
The correct answer will be option (B) total assets to equity, option ( C) net profit margins, and option (D) total assets turnover.
Three ratios that are used to mathematically produce the return on equity will be net profit margin along with net total Asset turnover and total assets to equity. This will help in deriving the return on equity.
The debt-to-total asset ratio shows the amount of a business possessed by leasers (individuals it has acquired cash from) contrasted and the number of the organization's resources claimed by investors. It is one of three estimations used to gauge the obligation limit, alongside the obligation overhauling proportion and the debt-to-equity ratio. The total debt-to-total-asset ratio is calculated by dividing a company's total debts by its total assets. By and large, debt to equity or debt to asset ratio below 1.0 would be viewed as moderately protected, though proportions of 2.0 or higher would be thought of as dangerous.
To learn more about equity ratios and debt,
https://brainly.com/question/28391877
#SPJ4
Find the points on the given curve where the tangent line is horizontal or vertical. (Assume 0 ≤ θ < π. Enter your answers as a comma-separated list of ordered pairs.) r = 8 cos θ Horizontal tangent (r, \Theta)= Vertical tangent (r, \Theta)=
Answers
Main Answer:The points on the given curve where the tangent line is horizontal are (8, 0), (-8, π), (8, 2π), (-8, 3π), and so on and the Vertical tangent are (0, π/2), (0, 3π/2), (0, 5π/2),so on.
Supporting Question and Answer:
How do we find points on a curve where the tangent line is horizontal or vertical?
To find points on a curve where the tangent line is horizontal or vertical, we need to determine the values of θ (or any parameter) that correspond to those points. This can be done by analyzing the derivatives of the curve equation and identifying the conditions under which the derivative is zero or undefined. Horizontal tangent lines occur when the derivative with respect to θ is zero, while vertical tangent lines occur when the derivative with respect to r is undefined or infinite.
Body of the Solution:To find the points on the curve r = 8 cos θ where the tangent line is horizontal or vertical, we need to determine the values of θ that correspond to those points.
Horizontal tangent line: A horizontal tangent line occurs when the derivative of r with respect to θ is equal to zero.Differentiating r = 8 cos θ with respect to θ, we get:
dr/dθ = -8 sin θ
Setting dr/dθ = 0, we have:
-8 sin θ = 0
Since sin θ = 0 when θ is an integer multiple of π, the values of θ that give a horizontal tangent line are: θ = 0, π, 2π, 3π, ...
For each value of θ, we can find the corresponding value of r by substituting it back into the equation r = 8 cos θ.
Vertical tangent line: A vertical tangent line occurs when the derivative of θ with respect to r is undefined or infinite.Differentiating r = 8 cos θ with respect to r, we get:
dθ/dr = -1 / (8 sin θ)
For a vertical tangent line, sin θ must be equal to zero, which occurs when θ is an integer multiple of π.
Therefore, the values of θ that give a vertical tangent line are: θ = π/2, 3π/2, 5π/2, ...
Again, for each value of θ, we can find the corresponding value of r by substituting it into the equation r = 8 cos θ.
Combining the values of θ and their corresponding values of r, we have: Horizontal tangent: (8, 0), (-8, π), (8, 2π), (-8, 3π), ... Vertical tangent: (0, π/2), (0, 3π/2), (0, 5π/2), ...
Final Answer:Thus, the points on the given curve where the tangent line is horizontal are (8, 0), (-8, π), (8, 2π), (-8, 3π), and so on, while the points where the tangent line is vertical are (0, π/2), (0, 3π/2), (0, 5π/2), and so on.
To learn more about the tangent line is horizontal or vertical from the given link
https://brainly.com/question/15288179
#SPJ4
The points on the given curve where the tangent line is horizontal are (8, 0), (-8, π), (8, 2π), (-8, 3π), and so on and the Vertical tangent are (0, π/2), (0, 3π/2), (0, 5π/2),so on.
How do we find points on a curve where the tangent line is horizontal or vertical?To find points on a curve where the tangent line is horizontal or vertical, we need to determine the values of θ (or any parameter) that correspond to those points. This can be done by analyzing the derivatives of the curve equation and identifying the conditions under which the derivative is zero or undefined. Horizontal tangent lines occur when the derivative with respect to θ is zero, while vertical tangent lines occur when the derivative with respect to r is undefined or infinite.
To find the points on the curve r = 8 cos θ where the tangent line is horizontal or vertical, we need to determine the values of θ that correspond to those points.
Horizontal tangent line: A horizontal tangent line occurs when the derivative of r with respect to θ is equal to zero.
Differentiating r = 8 cos θ with respect to θ, we get:
dr/dθ = -8 sin θ
Setting dr/dθ = 0, we have:
-8 sin θ = 0
Since sin θ = 0 when θ is an integer multiple of π, the values of θ that give a horizontal tangent line are: θ = 0, π, 2π, 3π, ...
For each value of θ, we can find the corresponding value of r by substituting it back into the equation r = 8 cos θ.
Vertical tangent line: A vertical tangent line occurs when the derivative of θ with respect to r is undefined or infinite.
Differentiating r = 8 cos θ with respect to r, we get:
dθ/dr = -1 / (8 sin θ)
For a vertical tangent line, sin θ must be equal to zero, which occurs when θ is an integer multiple of π.
Therefore, the values of θ that give a vertical tangent line are: θ = π/2, 3π/2, 5π/2, ...
Again, for each value of θ, we can find the corresponding value of r by substituting it into the equation r = 8 cos θ.
Combining the values of θ and their corresponding values of r, we have: Horizontal tangent: (8, 0), (-8, π), (8, 2π), (-8, 3π), ... Vertical tangent: (0, π/2), (0, 3π/2), (0, 5π/2), ...
Thus, the points on the given curve where the tangent line is horizontal are (8, 0), (-8, π), (8, 2π), (-8, 3π), and so on, while the points where the tangent line is vertical are (0, π/2), (0, 3π/2), (0, 5π/2), and so on.
To learn more about the tangent line
brainly.com/question/15288179
#SPJ4
17. Who am I? ___ Collection of one or more different types of variables, including arrays and pointers, that have been grouped under a single name for each manipulation.
a) template
b) array
c) structure
d) local variables
Answers
You are c) a structure. A structure is a collection of one or more different types of variables, including arrays and pointers, that have been grouped under a single name for each manipulation.
A structure is a user-defined data type that allows you to group together related data. For example, you could create a structure to store the name, age, and address of a person. The structure would have three variables, each of a different type: a string variable for the name, an integer variable for the age, and a string variable for the address.
The advantage of using a structure is that it allows you to treat the related data as a single unit. This makes it easier to manipulate the data and to pass the data to functions.
The other answer choices are incorrect. A template is a blueprint for creating a generic class or function. An array is a collection of elements of the same type. Local variables are variables that are declared within a function and that are only accessible within the function.
To learn more about integer variable click here : brainly.com/question/11873770
#SPJ11
evaluate the indefinite integrals below as infinite series. (a) ∫x^2e^3x2 dx(b) ∫x sin(4x^5) dx
Answers
The indefinite integral \($\int x^2e^{3x^2} dx\) evaluated as an infinite series is \(\frac{x^3}{3} + \frac{3x^5}{2! \cdot 5} + \frac{3^2 x^7}{3! \cdot 7} + \dots$\) and the indefinite integral \($\int x \sin(4x^5) , dx\)evaluated as an infinite series is \(\left(\frac{2}{7}x^7\right) - \left(\frac{4^3}{3! \cdot 13}x^{13}\right) + \left(\frac{4^5}{5! \cdot 19}x^{19}\right) - \left(\frac{4^7}{7! \cdot 25}x^{25}\right) + \ldots$\)
To evaluate the indefinite integral \($\int x^2 e^{3x^2} dx$\) as an infinite series, we can use the power series expansion of the exponential function.
The power series expansion of \(e^u\) is given by \($e^u = 1 + u + \frac{u^2}{2!} + \frac{u^3}{3!} + \dots$\)
Using this expansion, we can rewrite the integrand as \($x^2e^{3x^2} = x^2\left(1 + \left(3x^2\right) + \frac{\left(3x^2\right)^2}{2!} + \frac{\left(3x^2\right)^3}{3!} + \dots\right)$\)
Now, we can integrate each term of the series individually. The integral of \(x^2\) is \((x^3 / 3)\), and the integral of \(x^{2n}\) is \((x^{(2n+1)} / (2n+1)(n!))\) for n > 0.
Therefore, the integral becomes \($\int x^2e^{3x^2} dx = \frac{x^3}{3} + \frac{3x^5}{2! \cdot 5} + \frac{3^2 x^7}{3! \cdot 7} + \dots$\)
To evaluate the indefinite integral \($\int x \sin(4x^5) dx$\) as an infinite series, we can use the power series expansion of the sine function.
The power series expansion of sin(u) is given by \($\int x \sin(4x^5) dx = \int x \left(4x^5 - \frac{(4x^5)^3}{3!} + \frac{(4x^5)^5}{5!} - \frac{(4x^5)^7}{7!} + \ldots \right) dx$\)
Using this expansion, we can rewrite the integrand as \($x \sin(4x^5) = x \left(4x^5 - \frac{(4x^5)^3}{3!} + \frac{(4x^5)^5}{5!} - \frac{(4x^5)^7}{7!} + \ldots\right)$\)
Now, we can integrate each term of the series individually. The integral of \(x(4x^5)\) is \((2x^7)\), and the integral of \(x^(2n+1)\) is \((2x^{(2n+2)} / (2n+2))\) for n > 0.
Therefore, the integral becomes \($\int x \sin(4x^5) , dx = \left(\frac{2}{7}x^7\right) - \left(\frac{4^3}{3! \cdot 13}x^{13}\right) + \left(\frac{4^5}{5! \cdot 19}x^{19}\right) - \left(\frac{4^7}{7! \cdot 25}x^{25}\right) + \ldots$\)
Learn more about power series expansion here:
https://brainly.com/question/16774911
#SPJ11
Complete the proof.
help pls

Answers
Answer:
vertical, transitive, definition
Step-by-step explanation:
1 and 3 are vertical, as their opposite of each other
transitive means like if a = b and a =c then b = c
and a congruent to b means measure of angle a = measure of angle b
btw sugawara is cool
Inish earns $6. 25 for each car he washes. He always puts $25 of his weekly earnings into his college savings account. This week, Inish wants to have at least $45 spending money left after putting away his savings. What is the minimum number of cars he must wash? An inequality for the situation is 6. 25x – 25 ≥ 45. Inish must wash at least cars.
Answers
The minimum number of cars Inish must wash is 12.To find the minimum number of cars Inish must wash, we can solve the inequality 6.25x - 25 ≥ 45.
Starting with the inequality: 6.25x - 25 ≥ 45
Add 25 to both sides to isolate the term with x: 6.25x - 25 + 25 ≥ 45 + 25
Simplifying: 6.25x ≥ 70
Next, divide both sides of the inequality by 6.25 to solve for x: (6.25x)/6.25 ≥ 70/6.25
Simplifying: x ≥ 11.2
Since the number of cars must be a whole number, we round up to the nearest whole number to ensure Inish has at least $45 in spending money after saving $25. Therefore, the minimum number of cars Inish must wash is 12.
To learn more about minimum number click here : brainly.com/question/30164094
#SPJ11
Let T: R3 + R2 be the map TT (x, y, z) + (x2 + yz, ecyz) and w be the 2-form w = uvụ du 1 dv = Then calculate and simplify the following TW T*w Next, use this to calculate and simplify the following d(7*w) Do not use the fact that d(*W) = ** (dw). =
Answers
To calculate TW, substitute the coordinates (x, y, z) into T(x, y, z) = (x²+ yz, e^cyz). For Tˣw, substitute the coordinates (u, v) into Tˣw = u(x^2 + yz)dv. To calculate d(7ˣw), differentiate 7ˣw using exterior differentiation: d(7ˣw) = 7(du∧v + udv∧dv).
What is the calculation process for TW, Tˣw, and d(7ˣw) in the given scenario?The map T: R³ → R² is defined as T(x, y, z) = (x² + yz, e^cyz), and the 2-form w is given as w = uvdv.
To calculate TW, we substitute the coordinates (x, y, z) into the map T and obtain T(x, y, z) = (x² + yz, e^cyz).
Next, we calculate T³w by substituting the coordinates (u, v) into the 2-form w. Since w = uvdv, we have Tˣw = u(x² + yz)dv.
To calculate d(7ˣw), we differentiate the 2-form 7ˣw. Since w = uvdv, we have d(7ˣw) = d(7uvdv). Using the properties of exterior differentiation, we obtain d(7ˣw) = 7d(uv)∧dv = 7(du∧v + udv∧dv).
It's important to note that we are not using the fact that d(ˣw) = ˣˣ(dw) in this calculation.
Learn more about coordinates
brainly.com/question/22261383
#SPJ11
how many grams of sugar are there in a 200 ml glass of juice if there is 18.5 grams of sugar in 250ml of juice
Answers
There is 14.8 grams of sugar are there in a 200 ml glass of juice.
How do you define a unitary method?The term unitary corresponds to a specific or unique unit. As a result, the goal of this method is to determine the values in connection to a single unit. The unitary method is a technique that involves determining a value of a single unit and then calculating the value of the neccessary number of units based on that value.For the given question,
There are 18.5 gram of sugar in 250 ml of glass of juice.
This can be written as;
250 ml ------> 18.5 grams of sugar.
For 1 ml of the glass of juice, divide both sides by 250.
1 ml ------> 18.5/250 grams of sugar.
For 200 ml of the glass of juice, multiply both sides by 200.
200 ml ------> 18.5×200/250 grams of sugar.
200 ml ------> 14.8 grams of sugar.
Thus, 14.8 grams of sugar are there in a 200 ml glass of juice.
To know more about the unitary method, here
https://brainly.com/question/28540270
#SPJ1
La suma de dos números es 135 y su diferencia 37, hallar los dos números
Answers
Answer- 86 and 49
Step-by-step explanation: 86+49=135
86-49=37
a ² + b ² + 2 (ab + bc + ca)
Answers
Answer: = a^2 + 2ab + 2(ac+ b^2 + 2bc)
Step-by-step explanation:
The function h(n) gives the number of person-hours it takes to assemble n engines in a factory. What is a reasonable domain for h(n)?
Answers
Answer:
For example, if the function h(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the function.
Can yall help if you can I don’t understand this and I don’t wanna get behind in this class agin

Answers
Answer:
104 units
Step-by-step explanation:
You have the measurements you just need to add the numbers.
What is the solution to the system of equations below?
y = negative 3 x + 5 and y = 4 x minus 2
and there is no option choice of -2,-5
Answers
Step-by-step explanation:
please see my attachment

If in a population the rate of mutation that converts the A allele to the a allele is 10^-6 and the current frequency of the A allele is 0.75 and the a allele is 0.25, then the frequency of the A and a alleles in the next generation will be
Multiple Choice
O A: 0.74 a: 0.26
O A: 0.75000075 a: 0.24999925
O A: 0.75 a: 0.25
O A: 0.74999925 a: 0.25000075
Answers
The frequency of A allele after a single generation of mutation can be found as follows: Frequency of A allele after a single generationp(A) = p(A) x (1 - m) + q(a) x m
where,
m = mutation rate = 10^-6p(A) = frequency of A allele in initial generation = 0.75q(a) = frequency of a allele in initial generation = 0.25Thus,p(A) = 0.75 x (1 - 10^-6) + 0.25 x 10^-6 = 0.74999925
And the frequency of a allele will beq(a) = 1 - p(A) = 1 - 0.74999925 = 0.25000075
Therefore, the frequency of the A and a alleles in the next generation will beA: 0.74999925 and a: 0.25000075.
This is option D.
To know more about generation Visit:
https://brainly.com/question/12841996
#SPJ11
In a class, the ratio of the number of students with glasses to the number students who don't wear glasses is 1: 3. Find the percentage of students who don't wear glasses in the classroom.
Answers
Answer:
45
Step-by-step explanation:
1/3*100=the answer your get