Answers
Answer:
242 ft^2
Step-by-step explanation:
15 x 14 + 4 x 8 = 242 ft^2
(break down the polygon into two rectangles)
Related Questions
A coin sold at auction in 2019 for \( \$ 4,120,500 \). The coin had a face value of \( \$ 20 \) when it was issued in 1786 and had been previously sold for \( \$ 395,000 \) in \( 1968 . \) a. At what
Answers
The annual appreciation of the coin from 1968 to 2019 was 6.7%. Hence the coin appreciated at a rate of 6.7% per year from 1968 to 2019.
In 2019, a coin was sold at auction for $4,120,500. The coin had a face value of $20 when it was first issued in 1786. The coin had been previously sold for $395,000 in 1968. At what price did the coin appreciate annually from 1968 to 2019? Solution:We can start this problem by using the compound interest formula which is given as follows;A = P (1+r/n)^(nt)Where:A is the future value of the investment;P is the principal investment;r is the annual interest rate;n is the number of times that interest is compounded per year;t is the number of years the money is invested.To solve the problem we will consider the following;We will use the initial price of the coin which was sold in 1968 which is $395,000 as the principal investment, PWe will use the price of the coin sold at auction in 2019 which is $4,120,500 as the future value of the investment, AWe will use the number of years between 1968 and 2019 which is 51 years as t.The interest rate is not given, but we can solve for it by substituting the known values into the formula as shown below;A = P (1+r/n)^(nt)=> 4,120,500 = 395,000 (1+r/1)^(1 x 51)=> (1+r) = (4,120,500/395,000)^(1/51)=> (1+r) = 1.067=> r = 1.067 - 1=> r = 0.067 = 6.7%Therefore the annual appreciation of the coin from 1968 to 2019 was 6.7%. Hence the coin appreciated at a rate of 6.7% per year from 1968 to 2019.
Learn more about number here
https://brainly.com/question/3589540
#SPJ11
Let R Be The Region In The First Quadrant Bounded By X∧2+Y∧2=4,Y∧2=−X+4 And Y=0. Find The Volume Of The Solid
Answers
Let R be the region in the first quadrant bounded by x²+y² = 4, y² = −x+4 and y = 0. Find the volume of the solid.The volume of the solid formed by the given region can be found using the following formula:V = ∫aᵇ A(x)dx,where A(x) is the cross-sectional area of the solid with respect to x, and a, b are the limits of integration.
Let's first determine the limits of integration by finding the points of intersection between the given curves.
The curve x²+y² = 4 is a circle with center at (0, 0) and radius 2, while y² = −x+4 is a parabola opening to the left with vertex at (4, 0).Equating the two equations
:y² = −x+4x²+y² = 4x² − x + 4 = 0x = (1 ± √15)/2
Using the symmetry of the region, we only need to integrate from
0 to (1 + √15)/2.
A(x) is the area of the cross-section perpendicular to the x-axis. It is equal to πy².
Since the region is bounded by
y = 0, we have
A(x) = πy² = π(-x+4)² = π(x² - 8x + 16).
Therefore, the volume of the solid is:
V = ∫₀^((1 + √15)/2)
A(x)dx= ∫₀^((1 + √15)/2) π(x² - 8x + 16)
dx= π[1/3(x³ - 4x² + 16x)]₀^((1 + √15)/2)= π(1/3(((1 + √15)/2)³ - 4((1 + √15)/2)² + 16((1 + √15)/2)) - 16/3)≈ 13.98
Therefore, the volume of the solid is approximately 13.98.
To know more about quadrant bounded visit:
https://brainly.com/question/32507358
#SPJ11
Maximum Marks: 5 Given the total cost function TC=100Q−Q 2
+0.3Q 3
Where Q= rate of output and TC= total cost, determine a) The marginal and average cost functions. (2 Marks) b) The rate of output that results in minimum average cost. ( 3 Marks)
Answers
a) To find the marginal cost, we need to find the derivative of the total cost function with respect to the rate of output (Q).
TC = 100Q - Q² + 0.3Q³
Marginal cost (MC) = dTC/dQ
= d/dQ(100Q - Q² + 0.3Q³)
= 100 - 2Q + 0.9Q²
To find the average cost, we need to divide the total cost by the rate of output (Q).
Average cost (AC) = TC/Q
= (100Q - Q² + 0.3Q³)/Q
= 100 - Q + 0.3Q²
b) To find the rate of output that results in minimum average cost, we need to find the derivative of the average cost function with respect to Q. Then, we set it equal to zero and solve for Q.
AC = 100 - Q + 0.3Q²
dAC/dQ = -1 + 0.6Q
= 0-1 + 0.6Q
= 00.6Q
= 1Q
= 1/0.6Q
≈ 1.67
Therefore, the rate of output that results in minimum average cost is approximately 1.67.
Learn more about Marginal Cost:
https://brainly.com/question/30165613
#SPJ11
suppose that the radius is expanding at a rate of 0.6 inches per second. how fast is the volume changing when the radius is 2.3 inches? use at least 5 decimal places in your answer.
Answers
Using the theories of Application of derivative,we got that 59.11221inches³/sec is rate of volume changing when the radius is 2.3 inches.
We are given rate of change of radius (dr/dt)=0.6inches
We know very well that volume of sphere is given by (4/3)πr³
where r is the radius of the sphere.
Now, differentiating the volume with respect to radius, we get
=>dV/dr=4πr²
=>dV/dt=(dv/dr)·(dr/dt)
=>dV/dt=4πr².(dr/dt)
We are given that dr/dt=0.6inches/sec
So, dV/dt=4πr²·(0.6)
Now, putting values of r=2.3
dV/dt=4π(2.3)²×(0.6)
=>dV/dt=4×3.14×2.3×2.3×0.6
=>dV/dt=59.11221inches³/sec
Hence, if we suppose suppose that the radius is expanding at a rate of 0.6 inches per second, the volume is changing at the rate of 59.11221inches³/sec when the radius is 2.3 inches.
To know more about application of derivatives, visit here:
https://brainly.com/question/25120629
#SPJ4
use the flux form of green's theorem to evaluate ∫∫r2xy+12y3 da, where r is the triangle with vertices (0,0), (1,0), and (0,1). question content area bottom part 1 ∫∫r2xy+12y3 da=enter your response here (simplify your answer.)
Answers
To evaluate the given integral using Green's theorem, we need to express it in the flux form. The result of the integral is -r/6.
Green's theorem states that for a region R bounded by a simple closed curve C, the flux of the vector field F = (P, Q) across C is equal to the double integral of the curl of F over R.
In this case, we have the vector field F = (r^2xy, 1/2y^3), where r is the position vector (x, y).
The flux form of Green's theorem is:
\(∫∫R (curl F) · dA = ∫∫R (∂Q/∂x - ∂P/∂y) dA\)
Let's calculate the curl of F:
∂Q/∂x = 0
∂P/∂y = 2rxy
So, the curl of F is given by\((∂Q/∂x - ∂P/∂y) = 0 - 2rxy = -2rxy.\)
Now, let's evaluate the integral using the flux form of Green's theorem:
∫∫R (-2rxy) dA
Since the region R is a triangle with vertices (0,0), (1,0), and (0,1), we can express it as:
\(R = {(x, y) | 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 - x}\)
Now, we can rewrite the integral:
\(∫₀^(1-x) (-2rxy) dy = -2rxy²/2 ∣₀^(1-x) = -rxy² ∣₀^(1-x) = -r(x-x²)\)
Let's evaluate the inner integral first:
\(∫₀^(1-x) (-2rxy) dy = -2rxy²/2 ∣₀^(1-x) = -rxy² ∣₀^(1-x) = -r(x-x²)\)
Now, evaluate the outer integral:
\(∫₀¹ -r(x-x²) dx = -r(x²/2 - x³/3) ∣₀¹ = -r(1/2 - 1/3) = -r(3/6 - 2/6) = -r(1/6) = -r/6\)
Therefore, the result of the integral is -r/6.
Learn more about Green's theorem
https://brainly.com/question/27549150
#SPJ11
6. The desks at Ryder Middle School are shaped like a rectangle with an area of square inches. The length of the desk is inches. Write an expression to represent the width of the desk.
Answers
Answer:
x squared + x + 2
Step-by-step explanation:
no.
The base of a triangle is 6 inches more than 3 times the height. If the area of the triangle is 120 square inches.
find the base and height.
Answers
Answer:
2160
Step-by-step explanation:
6X3=18 so 120X18=2160
suppose there are 6 roads connecting town a to town b and 4 roads connecting town b to town c. in how many ways can a person travel from a to c via b?
Answers
Number of ways can a person travels from A to C via B = 24 ways
How it can be calculated that a person can travel in no. of ways?
To calculate the likelihood of an event occurring, we will apply the equation number of favourable outcomes divided by total number of outcomes. We sometimes need to apply a permutation to calculate the overall number of outcomes. A permutation is a method for calculating the number of events that occur when order is important.
Given,
Connection of roads from a = 6
Connection of roads from a = 4
Number of roads from a to b =6
Number of roads from b to c =4
Number of ways can a person travels from a to c via b
= 6*4
= 24 ways
The number of ways a person can go from A to C via B is 24.
To learn more about travel visit:
brainly.com/question/18090388
#SPJ4
What is the least common denominator of and 3/4 and 4/7?
Answers
Answer:
84
Step-by-step explanation:
if I'm wrong please let me know!!
Carl is building a fish tank for his fish. Carl wants the fish tank to be a cube. He knows his fish need 144 cubic inches of water to swim in. What is the length of the side on the aquarium that Juan will build?
Answers
Answer:
you need to multiply something
according to mark cherry, in 2008, in the united states, how many patients were waiting for and organ transplant/donation and how many actually received an organ transplant?
Answers
There are many more people awaiting such a transplant than there are available organs, leading to a large backlog of patients who are not able to receive an organ transplant.
In 2008, the United States Department of Health and Human Services reported that there were approximately 113,000 patients in the United States awaiting organ transplants. Of those, only 28,535 received an organ transplant that year. This is a ratio of approximately 1 in 4. This can be expressed mathematically as 28,535/113,000 = 0.25, or one fourth. This means that for every 4 people awaiting an organ transplant in the United States in 2008, only 1 actually received one. While organ transplants are a life-saving procedure for many, the reality is that there are many more people awaiting such a transplant than there are available organs, leading to a large backlog of patients who are not able to receive an organ transplant.
Learn more about ratio here:
https://brainly.com/question/13419413
#SPJ4
Complete question:What were the numbers of patients waiting for and receiving an organ transplant/donation in the United States in 2008, according to Mark Cherry?
Find the x ,trigonometry the law of sines

Answers
Using trigonometry the law of sines, the value of x is 21.27
What is trigonometry?In the field of mathematics known as trigonometry, correlations between angles and length ratios are studied. Trigonometry has a wide variety of identities. In order to simplify an expression, identify a more practical version of an expression, or solve an equation, trigonometric identities are frequently employed to rewrite trigonometrical expressions.
From the given diagram,
sin 62° = 40/ hyp
hyp = 40 / sin 62°
hyp = 40 / 0.8829
hyp = 45.31
now sin 28° = x/ hyp
x = hyp * sin 28°
x = 45.31 * 0.4695
x = 21.27
So, the value of x is 21.27
To learn more about trigonometry visit:
brainly.com/question/26719838
#SPJ1
if m is perpendicular to n, solve for x

Answers
x + 21 + 3x + 9 = 90
Combine like terms
4x + 30 = 90
Subtract 30 from both sides
4x = 60
Divide both sides by 4
x = 15
Answer:
x = 15
Step-by-step explanation:
You can use the opposite angles property to solve this problem. By using the property, the opposite angle of x+21 must also be x+21. So therefore, you can setup the equation x+21+3x+9=90. Simplify and you should get 4x+30=90. Subtract 30 on both sides and you get 4x=60. Divide 4 on both sides and you get x=15.
Which statements about the arcs and angles are true? select three options. ∠efd ≅ ∠egd ∠egd ≅ ∠ecd arc e d is-congruent-to arc f d marc e f = 60° marc f d = 120°
Answers
The true statements about the arcs and angles in circle C are:
∠EFD ≅ ∠EGD.Arc ED ≅ arc FD.m arc FD = 120°.How to analyze the arcs and angles?In Geometry, the sum of the measures of the interior angles in a quadrilateral is equal to 360°. Thus, we have:
m∠G + m∠GDC + m∠DCE + m∠GEC = 360°
60 + 90 + m∠DCE + 90 = 360
240 + m∠DCE = 360
m∠DCE = 360 - 240
m∠DCE = 120°.
Since ∠DFE is an inscribed angle that is subtended by arc DE, we have:
m∠DFE = m∠DCE
m∠DFE = 120
m∠DFE = 1/2 × 120
m∠DFE = 60°.
Therefore, ∠EFD ≅ ∠EGD.
From circle C, we can deduce that side ED is subtended by arc ED and side FD is subtended by arc FD (side ED ≅ side FD). Thus, arc ED ≅ arc FD and m arc FD is equal to 120°.
Read more on arcs and angles here: https://brainly.com/question/24043080
#SPJ1

Answer:
A C E
took quiz
HELP! THIS IS DUE TODAY, and i will mark brainlest!

Answers
Answer: The first one:
The graph is a function because each input has exactly one output.
Please mark brainliest. Hope this helps.
Seventh grade > R.12 Simplify expressions by combining like terms JJG
Simplify the expression:
7z+-6z + 10z
Answers
Answer:
11z
Step-by-step explanation:
7z+(-6z)= 1z or z
1z + 10z = 11z
Find the angle measurements of the intersections for the two equations f(x) = 4x - 5 and g(x) = 2x^2 - 5.
63 7 20 76 90
Answers
Without the specific formula, I'm unable to provide you with the exact angle measurements. But to find the angle measurements of the intersections for the two equations f(x) = 4x - 5 and g(x) = \(2x^2\) - 5, we need to find the values of x where the two equations intersect.
To do this, we can set the two equations equal to each other:
4x - 5 = \(2x^2\) - 5
Simplifying this equation, we get:
\(2x^2\) - 4x = 0
Factoring out 2x, we have:
2x(x - 2) = 0
Setting each factor equal to zero, we get two possible values for x: x = 0 and x = 2.
Now, we can substitute these values back into either equation to find the corresponding y-values.
For x = 0, substituting into f(x), we get:
f(0) = 4(0) - 5 = -5
For x = 2, substituting into f(x), we get:
f(2) = 4(2) - 5 = 3
So the coordinates of the intersection points are (0, -5) and (2, 3).
To find the angle measurements of the intersections, we need to calculate the slopes of the lines at these points.
For the line f(x) = 4x - 5, the slope is 4.
For the line g(x) = \(2x^2\) - 5, we need to find the derivative to calculate the slope. The derivative of g(x) is g'(x) = 4x.
Substituting x = 0 and x = 2 into g'(x), we get slopes of 0 and 8, respectively.
Using these slopes, we can find the angle measurements using the formula:
tan(angle) = (m1 - m2) / (1 + m1 * m2)
where m1 and m2 are the slopes of the lines.
Using this formula, we can calculate the angle measurements at the two intersection points.
However, without the specific formula, I'm unable to provide you with the exact angle measurements.
Learn more about angle
https://brainly.com/question/17039091
#SPJ11
Help please I don’t understand this please help me with the answer

Answers
Step-by-step explanation:
what is it asking? for the y intercept or gradient?
The slope is -1/1 and it crosses through the y-axis at -6. Slope intercept form is y = MX+B. M is the slope. B is the y-intercept.
find the three consecutive odd integers such that the product of the first and last integer is equal to 77 over 81 times the square of the middle integer.
Answers
Answer:
-11, -9 and -7
or
7, 9 and 11
Step-by-step explanation:
Let the middle number be x
Then the number before that is x - 2
The number after that is x + 2
This is because they are consecutive odd integers and odd integers are separated from the next or previous by 2
Product of first and last = (x - 2)(x+2)
(x - 2)(x + 2) = x² - 4 through the relationship (x - a)(x + a) = x² -a²
77 over 81 times the square of the middle = \(\dfrac{77}{81}x^2\)
Setting the two expressions equal to each other we get
\(x^2 - 4 = \dfrac{77}{81}x^2\\\\\)
Subtract \(\dfrac{77}{81}x^2\) from both sides:
\(x^2 - 4 -\dfrac{77}{81}x^2= 0\)
Add 4 to both sides:
\(x^2 - \dfrac{77}{81}x^2 = 4\\\\\)
\(x^2(1 - \dfrac{77}{81})= 4\\\\\)
\(1 - \dfrac{77}{81} = \dfrac{81}{81} - \dfrac{77}{81}= \dfrac{4}{81}\)
Therefore
\(x^2(1 - \dfrac{77}{81})= 4\\\\\\\rightarrow x^2 \cdot \dfrac{4}{81} = 4\\\\\\\)
Multiply both sides by 81:
\(81\cdot \dfrac{4}{81}x^2=4\cdot \:81\)
\(4x^2=324\)
\(x^2=81\)
\(x=\pm \sqrt{81}\\\\x=\sqrt{81},\:x=-\sqrt{81}\)
\(x=9,\:x=-9\)
This would be the middle integer
If x = -9, first integer = -9-2 = -11 and last integer = -9 + 2 = -7
If x = 9, first integer = 9-2 = 7 and last integer = 9 + 2 = -11
So the integers can be
-11, -9 and -7
or
7, 9 and 11
Evaluate the expression for v = 8
Answers
V = 8, because it can’t be simplified any further.
What is the equation in point-slope form for the line parallel to y = −6x + 1 that contains J(-6, 8)?
Answers
Step-by-step explanation:
the point-slope form is
y - y1 = a(x - x1)
"a" being the slope, (x1, y1) being the point on the line.
y = ax + b
is the slope-intercept form of a line.
again, "a" is the slope.
a parallel line must have the same slope.
so, our equation is
y - 8 = -6(x - -6) = -6(x + 6)
y - 8 = -6(x + 6)
The function g(x) is defined as
g(x) = 7x2 + 1. What is g(-2)?
Answers
Andrew is showing his work in simplifying −4.5 + 4.2 + 5.6 − 7.3. Identify any errors in his work or in his reasoning.

Answers
Answer:
D. Step 5Step-by-step explanation:
Andrew made a mistake at last step.
It should be:
-11.8 + 9.8 = 9.8 - 11.8 = -2 but not -21.6The sum of the numbers (112)3 and (211)3 is ( ____ )3 and their product is ( ____ )3.
Answers
(112)3 =336
(211)3 =633
sum of the numbers:
(112)3 +(211)3=
336+633=
969
product of the numbers:
(112)3 × (211)3=
336×633=
212688
for each this state, calculate predictions for the probability of measuring spin up and down along the x, y, and z axes, and confirm your predictions with the spins simulation. for the y and z components
Answers
To calculate the probabilities of measuring spin up and down along the y and z axes for a given quantum state:
For the x-component:
The probability of measuring spin up along the x-axis (P_x↑) is given by (|α|^2 + |β|^2)/2.
The probability of measuring spin down along the x-axis (P_x↓) is given by (|α|^2 + |β|^2)/2.
For the y-component:
The probability of measuring spin up along the y-axis (P_y↑) is given by |α|^2.
The probability of measuring spin down along the y-axis (P_y↓) is given by |β|^2.
For the z-component:
The probability of measuring spin up along the z-axis (P_z↑) is given by |α|^2.
The probability of measuring spin down along the z-axis (P_z↓) is given by |β|^2.
Please note that these calculations require knowing the coefficients α and β of the quantum state in question.
Learn more about quantum state here: brainly.com/question/14576222
#SPJ11
find the area 10ft 2 1/2
Answers
Answer:
if your trying to find the area of 10ft and 2 1/2 all you gotta do is turn the 2 1/2 in a decimal and multiply it by 10 which is 25
Step-by-step explanation:
What is the domain of the graph shown?
D:
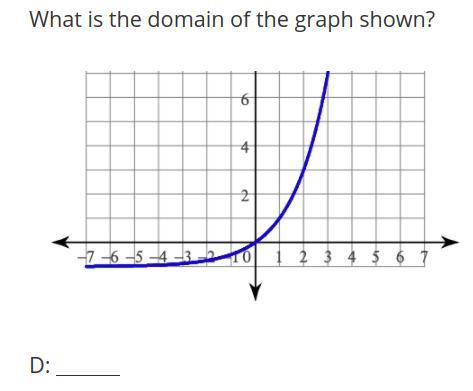
Answers
left to right so -infinity, 3
Explain how to convert an equation from slope-point from to slope-intercept fom.
Answers
Step-by-step explanation:
When you compare the two ways of writing a line, you might notice that there are some similarities. Both retain a y variable, an x variable and the slope of the line. So all you really need to get from point-slope form to slope-intercept form is a little algebraic manipulation. Consider the example given of a line in point-slope form: y + 5 = 3(x – 2).
Distribute x- Use the distributive property to simplify the right side of the equation:
Isolate the y Variable- Subtract 5 from both sides of the equation to isolate the y variable, which gives you the equation in point-slope form:
If an airplane descends 15 feet every 1.45 seconds, how far would the airplane travel in three and a half minutes? The equation is y=-40x+58
Answers
\(\qquad\qquad\huge\underline{{\sf Answer}}\)
Here we go ~
The air plane descends 15 feels every 1.45 seconds, so it's unit rate is :
\(\qquad \sf \dashrightarrow \: \dfrac{15}{1.45} \: \: ft / sec\)
Now we have to calculate the descent in 3.5 minutes ~
\(\qquad \sf \dashrightarrow \: \dfrac{15}{1.45} \: \: \times 3.5 \times 60\)
\(\qquad \sf \dashrightarrow \: 2172.41 \: \: ft\)
So, the airplane descends 2172.41 feels in three and a half minutes ~
: Prove that a) X'Y' + X'Y +XY = X' +Y b) A'BC' + ABC' + BC'D = BC' Find the complement of the following function a) WX(Y'Z+YZ') + W'X'(Y' +Z)(Y+Z') b) (A+B'+C') (A'B' +C)(A + B'C') Find Dual of question 2 (a, b),
Answers
a) X'Y' + X'Y + XY simplifies to X' + Y.
b) A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the functions:
a) Complement is W' + X' + YZ.
b) Complement is (A' + B + C)(A'B' + C' + A'B).
a) To prove X'Y' + X'Y + XY = X' + Y, we can use Boolean algebra identities:
X'Y' + X'Y + XY
= Y'(X' + X) + XY(Distributive Law)
= Y' + XY(X + X' = 1)
= X' + Y(Commutative Law)
Therefore, X'Y' + X'Y + XY simplifies to X' + Y.
b) To prove A'BC' + ABC' + BC'D = BC', we can simplify the expression using Boolean algebra:
A'BC' + ABC' + BC'D
= BC'(A' + A) + BC'D (Distributive Law)
= BC' + BC'D(A + A' = 1)
= BC'(BC' + BC'D = BC' + BC'(1) = BC')
Hence, A'BC' + ABC' + BC'D simplifies to BC'.
Complement of the given functions:
a) The complement of WX(Y'Z + YZ') + W'X'(Y' + Z)(Y + Z') is W' + X' + YZ.
b) The complement of (A + B' + C')(A'B' + C)(A + B'C') is (A' + B + C)(A'B' + C' + A'B).
Learn more About Distributive Law from the given link
https://brainly.com/question/25224410
#SPJ11
