What is the solution to the system of equations
y=3x-8
Y=4-x
A (-3,1)
B (3,-1)
C(3,1)
D(1,3)
Answers
There is the answer and also a check to make sure hope this helps

The solution to the system of equations is (3, 1)
The given system of equations is
y = 3x - 8.........(1)
y = 4 - x...........(2)
Compare equations (1) and (2)
3x - 8 = 4 - x
Collect like terms
3x + x = 4 + 8
4x = 12
Divide both sides by 4
4x / 4 = 12/4
x = 3
To get the value of y, substitute x = 3 into equation (2)
y = 4 - x
y = 4 - 3
y = 1
Therefore, the solution to the system of equations is (3, 1)
Learn more about system of equations here:
https://brainly.com/question/25976025
Related Questions
Triangular prism problem
Help, I’m trying to solve this question but I’m stuck on what the length is for the right angle in pink

Answers
The total surface area of the triangular prism is: 111 ft²
What is the surface area of the triangular prism?To find the total surface area of the given triangular prism, we will find the area of all the surfaces and add it up.
Formula for the area of a rectangle is:
Area = Length * Width
Area of a triangle is:
Area = ¹/₂ * base * height
Thus:
Total Surface area = 2(¹/₂ * 3 * 7) + (7 * 5) + (8 * 5) + (3 * 5)
Total Surface area = 21 + 35 + 40 + 15
Total Surface area = 111 ft²
Read more about Triangular Prism Surface area at: https://brainly.com/question/12410386
#SPJ1
What is the product of five and a number, decreased by eleven
Answers
Answer:
5x-11
Step-by-step explanation:
This is the word problem as an expression
5x-55 represents the mathematical expression for the given statement.
What is an expression?Expressions in maths are mathematical statements that have a minimum of two terms containing numbers or variables, or both, connected by an operator in between.
Given is a statement, the product of five and a number, decreased by eleven,
Let the number be x, converting the given statement, into a mathematical expression, we get
5(x-11)
= 5x-55
Hence, 5x-55 represents the mathematical expression for the given statement.
For more references on expressions, click;
https://brainly.com/question/14083225
#SPJ2
find the 49th term of a sequence with a=50 and D=4
Answers
Answer:
a=50
d=4
Then
Sn=n÷2 (2a+(n_1)d)
S49=49÷2 (2×50+(49-1)4)
=7154
q(x)=1/3x-2 ; q(x)=-4
Answers
The value of x when q (x) = -4 as given in the task content and required to be evaluated is; -6.
What is the value of x when q (x) = -4?It follows from the task content that the premise function given is; q ( x ) = 1/3x - 2 and hence,the value of x for which the function instance q (x) = -4 is to be determined.
Since the given function is;
q ( x ) = 1/3x - 2
It follows that when q (x) = -4; the value of x can be determined as follows;
-4 = 1/3x - 2
-4 + 2 = ( 1/ 3) x
-2 = ( 1 / 3 ) x
Hence, by cross-multiplication; we have the value of x to be;
x = -2 × 3
x = -6.
Therefore, the required value of x for which the function, q (x) = -4 is; -6.
Read more on function evaluation;
https://brainly.com/question/2284360
#SPJ1
Please help ASAP this is a some homework I need help with

Answers
Answer:
I believe that the answer is 1.4 because if you do all of the math out you get 1,390,000 km which then you put into scientific notation which is 1.4x10 raised to the 4
Step-by-step explanation:
oops i put it up there. Hope that this was helpful.
Coin Flips: If you flip a fair coin 6 times, what is the probability of each of the following? (please round all answers to 4 decimal places) a) getting all tails? b) getting all heads? c) getting at least one tails?
Answers
a) The probability of getting all tails is 0.0156.
b) The probability of getting all heads is also 0.0156.
c) There is a 0.9844 percent chance of at least one tail.
The probability of getting tails on a single coin flip is 0.5, and the same goes for getting heads. We can use this information to calculate the probabilities for the given scenarios:
a) Getting all tails:
The probability of getting tails on the first flip is 0.5. Since each flip is independent, the probability of getting tails on the second flip is also 0.5, and the same goes for the remaining flips. We can calculate the probability of getting all tails by multiplying these probabilities together:
P(all tails) = 0.5 x 0.5 x 0.5 x 0.5 x 0.5 x 0.5 = 0.0156
So the probability of getting all tails is 0.0156.
b) Getting all heads:
We can use the same reasoning as in part (a) to calculate the probability of getting all heads:
P(all heads) = 0.5 x 0.5 x 0.5 x 0.5 x 0.5 x 0.5 = 0.0156
So the probability of getting all heads is also 0.0156.
c) Getting at least one tails:
To calculate this probability, we can use the complement rule: the probability of an event occurring is equal to 1 minus the probability of the event not occurring. In this case, the event we're interested in is getting at least one tails, so we can calculate the probability of getting no tails and subtract that from 1:
P (at least one tails) = 1 - P (no tails)
To get no tails, we would have to get heads on every flip. We can use the same probability calculation as in parts (a) and (b) to find the probability of getting heads on all six flips:
P(all heads) = 0.5 x 0.5 x 0.5 x 0.5 x 0.5 x 0.5 = 0.0156
So the probability of getting no tails is 0.0156, and the probability of getting at least one tails is:
P(at least one tails) = 1 - P(no tails) = 1 - 0.0156 = 0.9844
So, There is a 0.9844 percent chance of at least one tail.
for such more question on probability
https://brainly.com/question/13604758
#SPJ4
Ingnd mxes 3 6 pounds of almonds with some raisins to make a trail mix She divides the trail mix into 12 equal portions Each portion weighs 0.7 of a pound How many pounds of raisins did she use to make the trail mix? Express the answer to the nearest tenth 2.9 4.8 5.1 7.2
Answers
Answer:
The 12 portions weigh a total of 12*0.7 = 8.4 lbs
So, the almonds weigh 8.4 - 3.6 = 4.8 lbs
Answer:
4.8 poundsStep-by-step explanation:
Let raisins weight be x
Then we get equation
(3.6 + x)/12 = 0.7Solving for x
3.6 + x = 12*0.7x + 3.6 = 8.4x = 8.4 - 3.6x = 4.8 poundsOption B is correct one
can someone help me please? the last point of the first graph ends on 6

Answers
Answer:
a) Yes
b) for reference, draw the line y = x, and reflect it over that, this reflection will be your inverse. Or switch the x and y values of each point of the function.
Here is a photo of the original function in black, it's inverse in red, and the line of reflection y = x in blue:
c) No, because it fails the vertical line test, when you draw a vertical line across the inverse function, it hits it more than once.
d) Domain of the original function: -6 ≤ x ≤ 6 ; x(the domain) is greater than or equal to -6 and less than or equal to 6.
e) Domain of inverse function: 0 ≤ x ≤ 4 ; x(the domain) is greater than or equal to 0 and less than or equal to 4.
f) Range of the original function: 0 ≤ y ≤ 4 ; y(the range) is greater than or equal to 0 and less than or equal to 4.
e2) Range of the inverse function: -6 ≤ y ≤ 6 ; y(the range) is greater than or equal to -6 and less than or equal to 6.
f2) x-intercept of original function: -6
g) y-intercept of the inverse function: -6
h) x-intercept of the inverse function: 4
i) y-intercept of the original function: 4
j) (2,2) or any point where the x, and y are the same within the function, or the point where the function intersects y = x.

A. -22
B. 11
C. 13
D. 26

Answers
D. 26
\(2n - 3 : 8\)
8. The length of a rectangular picture is 4 inches longer than three times the width. If the
perimeter is 56 inches, find the dimensions of the picture.
Answers
Answer:
The dimensions of the picture are 8 inches and 20 inches
Step-by-step explanation:
A rectangular picture has a length 4 inches longer than three times the width, so assume that the width of the rectangle is x.
∵ The width of the rectangle = x inches
∵ Three times the width = 3 times x = 3x
∵ Four less than 3 times width = 3x - 4
∴ The length = 3x - 4 inches
Perimeter (P) of a rectangle = 2 length + 2 width, then substitute the length and the width by their values above.
∴ P = 2(x) + 2(3x - 4)
∵ P = 56 inches ⇒ given
∴ 56 = 2(x) + 2(3x - 4)
→ Simplify the right side
∵ 2(3x - 4) = 2(3x) - 2(4) = 6x - 8
∴ 56 = 2x + 6x - 8
→ Add the like terms in the right side
∴ 56 = (2x + 6x) - 8
∴ 56 = 8x - 8
→ Add 8 to both sides to move 8 from the right side to the left side
∴ 56 + 8 = 8x - 8 + 8
∴ 64 = 8x
→ Divide both sides by 8 to find x
∴ \(\frac{64}{8}=\frac{8x}{8}\)
∴ 8 = x
∵ x represents the width of the picture
∴ The width of the picture is 8 inches.
∵ 3x - 4 represents the length of the picture
∴ The length = 3(8) - 4 = 24 - 4 = 20
∴ The length of the picture is 20 inches.
For safety, the slope of a staircase must be > 0.58 and < 0.70. a staircase has a vertical rise of 2.4m over a horizontal run of 3.5m.
Answers
a) The slope of the staircase is 2.4/3.5 = 0.6857 (rounded to four decimal places). b) Yes, the staircase is safe as its slope falls within the required range of 0.58 to 0.70.
a) The slope of a staircase is calculated by dividing the vertical rise by the horizontal run. So, the slope of this staircase is:
slope = vertical rise / horizontal run
= 2.4 m / 3.5 m
= 0.686
b) To determine if the staircase is safe, we need to compare the slope with the safety requirement of 0.58 < slope < 0.70. In this case, the slope of the staircase is within the safety range, as 0.58 < 0.686 < 0.70. Therefore, the staircase is safe according to the safety requirement.
Learn more about slope here: brainly.com/question/3605446
#SPJ4
Show the family of conics with the same focus
x^2/a^2+C + y^2/b^2+C = 1
is its own orthogonal family of curves.
Answers
The original equation and the orthogonal equation are the same, we can conclude that the family of conics with the same focus x^2/a^2+C + y^2/b^2+C = 1 is its own orthogonal family of curves.
To show that the family of conics with the same focus x^2/a^2+C + y^2/b^2+C = 1 is its own orthogonal family of curves, we need to take the derivative of the equation and set it equal to -1/b^2, the slope of the orthogonal line.
First, we take the derivative of the equation with respect to x:
2x/a^2 = -2y/b^2 * dy/dx
Simplifying, we get:
dy/dx = -b^2*x/a^2*y
Now, we set this equal to -1/b^2:
-b^2*x/a^2*y = -1/b^2
Cross-multiplying and simplifying, we get:
x/a^2*y = 1/b^2
Finally, we can rearrange this equation to get:
y = b^2*x/a^2
This equation represents the orthogonal family of curves to the original family of conics. Since the original equation and the orthogonal equation are the same, we can conclude that the family of conics with the same focus x^2/a^2+C + y^2/b^2+C = 1 is its own orthogonal family of curves.
Learn about Conics
brainly.com/question/29767685
#SPJ11
8 kg of potatoes and 5 kg of carrots cost $28 whereas 2 kg of potatoes and 3 kg of carrots cost $11.20. Find the cost of 1 kg of each item.
also give the explanation.
Answers
Answer:
Step-by-step explanation:
Cost of 1 kg of Potatoes = $ 2
Cost of 1 kg of Carrots = $ 2.40
Let the cost of 1 kg of Potatoes = x
Let the cost of 1 kg of Carrots = y
ATQ , 8x + 5y = 28 - 1)
2x + 3y = 11.20 - 2)
Multiplying 2) by 4
8x + 12y = 44.80 - 3)
Applying Elimination method in 1) and 3)
8x + 5y = 28.00
8x + 12y = 44.80
0 + -7y = - 16.80
y = 16.8/7
y = 2.4
Putting the value of "y" in 1)
8x + 5(2.4) = 28
8x + 12 = 28
8x = 16
x = 16/8
x = 2
find the sum of 3x,(1-6x),4x and x
Answers
Answer:
2x+1
Step-by-step explanation:
S=3x+(1-6x)+4x+x=3x-6x+4x+x+1=2x+1
You are required to: a.Rewrite the formulation above in the standard form by adding the required variables to replace the inequalities. b.Find a solution for the above formulation utilizing the linear programming simplex method.
Answers
Using the simplex method, the optimal solution for the given linear programming problem is x = 2, y = 2, z = 0, with the maximum objective value of P = 10.
a. To rewrite the formulation in standard form, we need to replace the inequalities with equality constraints and introduce non-negative variables. Let's assume x, y, and z as the non-negative variables:
Maximize P = 3x + 2y + 4z
Subject to:2x + y + z + s1 = 8
x + 2y + 3z + s2 = 10
x, y, z ≥ 0
b. Utilizing the linear programming simplex method, we can solve the above formulation. After setting up the initial tableau, we perform iterations by selecting a pivot element and applying the simplex algorithm until an optimal solution is reached. The algorithm involves row operations to pivot the tableau until all coefficients in the objective row are non-negative. This ensures the optimality condition is satisfied, and the maximum value of P is obtained.
To provide a brief solution within 120 words, we determine the optimal solution by applying the simplex method to the above formulation. After performing the necessary iterations, we find that the maximum value of P occurs when x = 2, y = 2, z = 0, with P = 10. Therefore, the maximum value of P is 10, and the solution for the given problem is x = 2, y = 2, and z = 0.
To learn more about simplex method click here
brainly.com/question/32298193
#SPJ11
find the lemgth of arc PQ

Answers
The arc length is D) 3.14 meters.
What is arc length?
In mathematics, an arc is a portion of a curve that can be thought of as a segment of the curve. An arc is a connected set of points on a curve, usually a portion of a circle.
It is defined by two endpoints and all the points along the curve between them. The length of an arc is the distance along the curve between its two endpoints.
The distance along the curved line that forms the arc (a section of a circle) is measured using the arc length formula.
\(A_L=\frac{\theta}{360\textdegree}2\pi r\)
Here the give circle Radius PR = 3m and θ=60°.
Now using arc length formula then,
=> Arc length \(A_L=\frac{\theta}{360\textdegree}2\pi r\)
=> \(A_L=\frac{60}{360} \times2\times3.14\times3\)
=> \(A_L=\frac{1}{6}\times2\times3.14\times3\)
=> \(A_L\) = 3.14 m.
Hence the arc length is D) 3.14 meters.
Learn more about Arc length at
https://brainly.com/question/28108430
#SPJ1
graph a line with a slope of -7, 4and has a slope of -2/3
Answers
Answer:
-2/3 then -7, 4


The figure is made of rectangular prisms. What is the volume?
Please answer quickly.
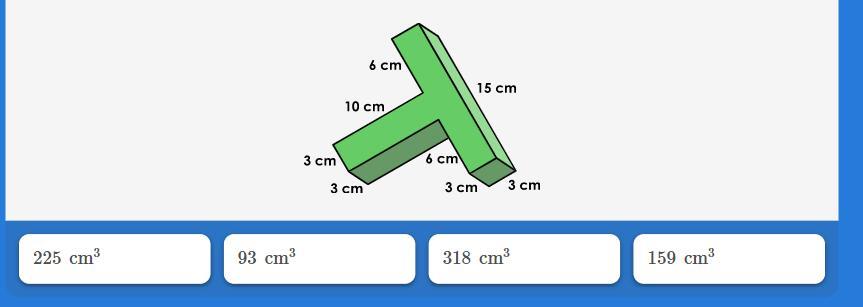
Answers
hope this helps
rationalize the denominator of $\frac{5}{2-\sqrt{3}}$, and write your answer in the form $\displaystyle{\frac{a b\sqrt{3}}{c}}$ where the fraction is in lowest terms. what is $a b c$?
Answers
The value of a+b+c will be 16 if \(\frac{5}{2-\sqrt{3}}\) rationalize as \(\displaystyle{\frac{a + b\sqrt{3}}{c}}\).
Given,
y = \(\frac{5}{2-\sqrt{3}}\)
To solve the given expression we multiply the numerator and denominator by the conjugate of the denominator
\(= \frac{5}{2-\sqrt{3}} \frac{2+\sqrt{3} }{2+\sqrt{3}}\)
\(= \frac{10+5\sqrt{3} }{2^2 - \sqrt{3}^2 }\)
\(= \frac{10+5\sqrt{3} }{4-3 }\)
\(= \frac{10+5\sqrt{3} }{1 }\) = \(\displaystyle{\frac{a + b\sqrt{3}}{c}}\)
Now, by comparing the result we get
a = 10, b = 5, c = 1
hence, a+b+c = 10+5+1 = 16
Therefore, the value of a+b+c will be 16.
#SPJ4
To learn more about conjugate:
https://brainly.com/question/28977490
suppose the weights of largemouth bass in a lake are right skewed with mean 1.50 pounds and standard deviation 0.3 pounds. a sample of 40 largemouth bass from the lake are selected at random. (a) find the mean and standard deviation of the sampling distribution of the mean weight per fish.
Answers
The mean of the distribution of the mean weight per fish based on the sampling is 1.50 pounds, and the standard deviation is 0.06 pounds.
These formulas can be used to calculate the mean and standard deviation of the sampling distribution of mean fish weight:
Mean of the mean weight per fish sampled across the distribution:
μ = μ = 1.50 pounds (mean weight of a single fish)
The sampling distribution's standard deviation for the mean fish weight is:
σ/√n = 0.3/√40 = 0.06 pounds (where n is the sample size and is the standard deviation of the weight of a single fish.)
So, The mean of the distribution of the mean weight per fish based on the sampling is 1.50 pounds, and the standard deviation is 0.06 pounds.
To learn more about standard deviation visit the link below:
https://brainly.com/question/23907081
#SPJ4
Pythagorean Theorem Question! Please help

Answers
Answer:
It is the fourth one.
Step-by-step explanation: You use it to find it to see if it is a right triangle.
if the value of c is negative, you would need zero pairs to model the factorization of the polynomial. the x-tiles on the board determine what the constants are in the factors. the product of these constants is equal to the value of c, so you would need positive tiles on one side of the x-squared tile and negative x-tiles on the other side to have opposite signs on the constants. opposite signs on the constants will result in a negative value for c when multiplying the factors.
Answers
Answer:
value of c is negative
constant are in factor bla bla.
Step-by-step explanation:
PLEASE ANSWER ASAP
The sum of the first six terms of the geometric sequence 1, 2, 4, 8, ... is equal to the sum of
the first six terms of an arithmetic sequence that also has 1 as its first term. What is the
fifth term of the arithmetic sequence?
Answers
Answer:
FIND IT YOURSELF
Step-by-step explanation:
YOU ARE GIVEN QUESTIONS TO ANSWER FOR YOU, NOW DO IT YOURSELF.
The following parametric equations trace out a loop.
x=9-(4/2)t^2
y=(-4/6) t^3+4t+1
Find the t values at which the curve intersects itself: t=± _____
What is the total area inside the loop? Area ______
Answers
Answer: Therefore, the total area inside the loop is (32/15)\(\sqrt{3}\) square units.
Step-by-step explanation:
To find the t values at which the curve intersects itself, we need to solve the equation x(t1) = x(t2) and y(t1) = y(t2) simultaneously, where t1 and t2 are different values of t.
x(t1) = x(t2) gives us:
9 - (4/2)t1^2 = 9 - (4/2)t2^2
Simplifying this equation, we get:
t1^2 = t2^2
t1 = ±t2
Substituting t1 = -t2 in the equation y(t1) = y(t2), we get:
(-4/6) t1^3 + 4t1 + 1 = (-4/6) t2^3 + 4t2 + 1
Simplifying this equation, we get:
t1^3 - t2^3 = 6(t1 - t2)
Using t1 = -t2, we can rewrite this equation as:
-2t1^3 = 6(-2t1)
Simplifying this equation, we get:
t1 = ±sqrt(3)
Therefore, the curve intersects itself at t = +\(\sqrt{3}\) and t = -\(\sqrt{3}\)
To find the total area inside the loop, we can use the formula for the area enclosed by a parametric curve:
A = ∫[a,b] (y(t) x'(t)) dt
where x'(t) is the derivative of x(t) with respect to t.
x'(t) = -4t
y(t) = (-4/6) t^3 + 4t + 1
Therefore, we have:
A = ∫[-\(\sqrt{3}\),\(\sqrt{3}\)] ((-4/6) t^3 + 4t + 1)(-4t) dt
A = ∫[-\(\sqrt{3}\)),\(\sqrt{3}\)] (8t^2 - (4/6)t^4 - 4t^2 - 4t) dt
A = ∫[-\(\sqrt{3}\),\(\sqrt{3}\)] (-4/6)t^4 + 4t^2 - 4t dt
A = [-(4/30)t^5 + (4/3)t^3 - 2t^2] [-\(\sqrt{3}\),\(\sqrt{3}\)]
A = (32/15)\(\sqrt{3}\)
Therefore, the total area inside the loop is (32/15)\(\sqrt{3}\) square units.
To Know more about curve refer here
https://brainly.com/question/29990557#
#SPJ11
Plz help it’s due tonight!!!

Answers
Answer:
x = 12
A = 83
B = 38
c = 59
Step-by-step explanation:
Viking Voyager specializes in the design and production of replica Viking boats. On January 1, 2021, the company issues $2,900,000 of 9% bonds, due in 20 years, with interest payable semiannually on June 30 and December 31 each year.
Required:
1. If the market interest rate is 9%, the bonds will issue at $2,900,000. Record the bond issue on January 1, 2021, and the first two semiannual interest payments on June 30, 2021, and December 31, 2021. (If no entry is required for a particular transaction/event, select "No Journal Entry Required" in the first account field.)
2. If the market interest rate is 10%, the bonds will issue at $2,651,193. Record the bond issue on January 1, 2021, and the first two semiannual interest payments on June 30, 2021, and December 31, 2021. (If no entry is required for a particular transaction/event, select "No Journal Entry Required" in the first account field. Round your answers to the nearest dollar amount.)
3. If the market interest rate is 8%, the bonds will issue at $3,186,995. Record the bond issue on January 1, 2021, and the first two semiannual interest payments on June 30, 2021, and December 31, 2021. (If no entry is required for a particular transaction/event, select "No Journal Entry Required" in the first account field. Round your answers to the nearest dollar amount.)
Answers
The bond issue and interest payments are recorded differently based on the market interest rate.
How to find the bond issue and interest payments recorded based on the market interest rate?The recording of bond issue and interest payments depends on the market interest rate. When the market interest rate is equal to the stated rate of 9%, the bonds will issue at their face value of $2,900,000.
On January 1, 2021, the company would debit Cash for $2,900,000 and credit Bonds Payable for $2,900,000 to record the bond issue.
The interest payments on June 30, 2021, and December 31, 2021, would be recorded by debiting Interest Expense for $130,500 ([$2,900,000 * 9%]/2) and crediting Cash for $130,500.
However, when the market interest rate is 10% or 8%, the bonds will issue at a discount or premium, respectively. If the market interest rate is 10%, the bonds will issue at $2,651,193 (rounded).
In this case, the bond issue on January 1, 2021, would be recorded by debiting Cash for $2,651,193 and crediting Discount on Bonds Payable for $248,807 ($2,900,000 - $2,651,193).
The interest payments on June 30, 2021, and December 31, 2021, would be recorded as mentioned earlier.
Conversely, if the market interest rate is 8%, the bonds will issue at $3,186,995 (rounded).
The bond issue on January 1, 2021, would be recorded by debiting Cash for $3,186,995 and crediting Premium on Bonds Payable for $286,995 ($3,186,995 - $2,900,000).
The interest payments on June 30, 2021, and December 31, 2021, would be recorded accordingly.
Learn more about bond issue
brainly.com/question/14599790
#SPJ11
Gina Wilson unit 5 : homework 6: Slope-Intercept Form
Answers
The slope-intercept form of the equation of the line is y = x + 6.
What is an equation of the line?A linear equation with a degree of one is referred to as an equation of the line. Two variables, x, and y, are present in the equation of the line. The third parameter is the line's slope, which indicates the line's elevation.
The equation of the line's general form is:
y = mx + c
m = slope
c = y-intercept
Slope = ( y₂ - y₁ ) / ( x₂ - x₁ )
The formula for calculating the line's slope is
Slope = ( 6 - 4) / ( 2 - 0)
Slope = 1
The y-intercept will be calculated as:-
y = mx + c
y = x +c
6 = c
The equation of the line can be written as:-
y = x + 6
To know more about an equation of the line follow
https://brainly.com/question/18831322
#SPJ9
over the summer, you read 20 books. Eight of these books were biographies.
a. find the ratio of biographies to the total number of books.
b. find the ratio of non-biographies to biographies
c. find the ratio of non-biographies to the total of the number of books.
Answers
Answer:
A. \(\frac{2}{5}\)
B. \(\frac{3}{2}\)
C. \(\frac{3}{5}\)
Step-by-step explanation:
A. 8:20
4: 10
2: 5 = \(\frac{2}{5}\)
B. 12: 8
3: 2 = \(\frac{3}{2}\)
C. 12: 20
3: 5 = \(\frac{3}{5}\)
On a map, 2 inches represents 350 miles. If the distance between 2 cities
is 875 miles, how many inches apart are they on the map?
Answers
Answer:
5 INCHES
Step-by-step explanation:
If 2 inches = 350 miles
then 1 inch is 350%2 which is 175
So 875 % 175 = 5 inches
Y is directly proportional to x when y=30 x=6. Work out an equation connectng y and x
Answers
The equation connecting y and x when y is directly proportional to x and y = 30 when x = 6 is y = 5x.
If y is directly proportional to x, we can write the equation in the form:
y = kx
where k is the constant of proportionality.
To find k, we can use the values of y and x given:
y = 30, x = 6
When we enter these values into the formula above, we obtain:
30 = k * 6
Solving for k, we get:
k = 30/6 = 5
Therefore, the equation connecting y and x when y is directly proportional to x is:
y = 5x
When two variables are directly proportional, it means that when one variable increases or decreases, the other variable changes in the same proportion. In this scenario, we are given that y is directly proportional to x and we are also given a specific point on the line, (6, 30). Using this information, we can solve for the constant of proportionality k and write the equation connecting y and x as y = kx, where k is 5.
Learn more about equation here:
https://brainly.com/question/29174899
#SPJ4