What is the y-intercept of the function f(x) = -2/9x + 1/3?
Answers
Answer:
The y intercept would be (0, 1/3)
The number at the end is always the y value. In a y intercept x is always 0.
Related Questions
A car rental agency charges $15 a day for driving a car 200 miles or less. If a car is driven over 200 miles, the renter must pay $0.05 for each mile over 200 driven. Which of the following functions represents the cost to drive a car from this agency miles x a day?

Answers
The function which represents the cost to drive a car from this agency miles x a day is :
C(x) = 15, if 0 ≤ x ≤ 200
= 15 + 0.05x, if x > 200
Given that,
A car rental agency charges $15 a day for driving a car 200 miles or less.
The function can be written as,
C(x) = 15 if 0 ≤ x ≤ 200
If a car is driven over 200 miles, the renter must pay $0.05 for each mile over 200 driven.
C(x) = 15 + 0.05x, if x > 200
Hence the correct option is D.
Learn more about Functions here :
https://brainly.com/question/29067911
#SPJ1
‼️WILL MARK BRAINLIEST‼️

Answers
The theoretical probability that the coin will land tails up is 1/2 = 0.5 or 50%.
How to calculate a probability?A probability is calculated as the division of the desired number of outcomes by the total number of outcomes in the context of a problem/experiment.
In this problem, we have a fair coin, meaning that in any throw, the coin is equally as likely to land in one of the two outcomes, which are heads up or tails up.
Hence the probability is given as follows:
p = 1/2 = 0.5 = 50%.
More can be learned about probability at https://brainly.com/question/24756209
#SPJ1
Write an expression, using an exponent, that is equivalent to 8\times8\times8\times8
.
Answers
Answer:
8^3
Step-by-step explanation:
8*8*8 is equivalent to 8^3 which equals a total of 512 units
Find the length of the diagonal for a square that is 6 cm. by 6 cm. Leave answer in simple radical form, if necessary.
please hurry I beg
Answers
Answer:
\(6\sqrt{2}\)
Step-by-step explanation:
let the diagonal be d
using the pythagoras theorem,
\(6^{2} + 6^{2} = d^{2}\)
\(d=\sqrt{72}\)
which in radical form is
\(6\sqrt{2}\)
hi can you help it will help me
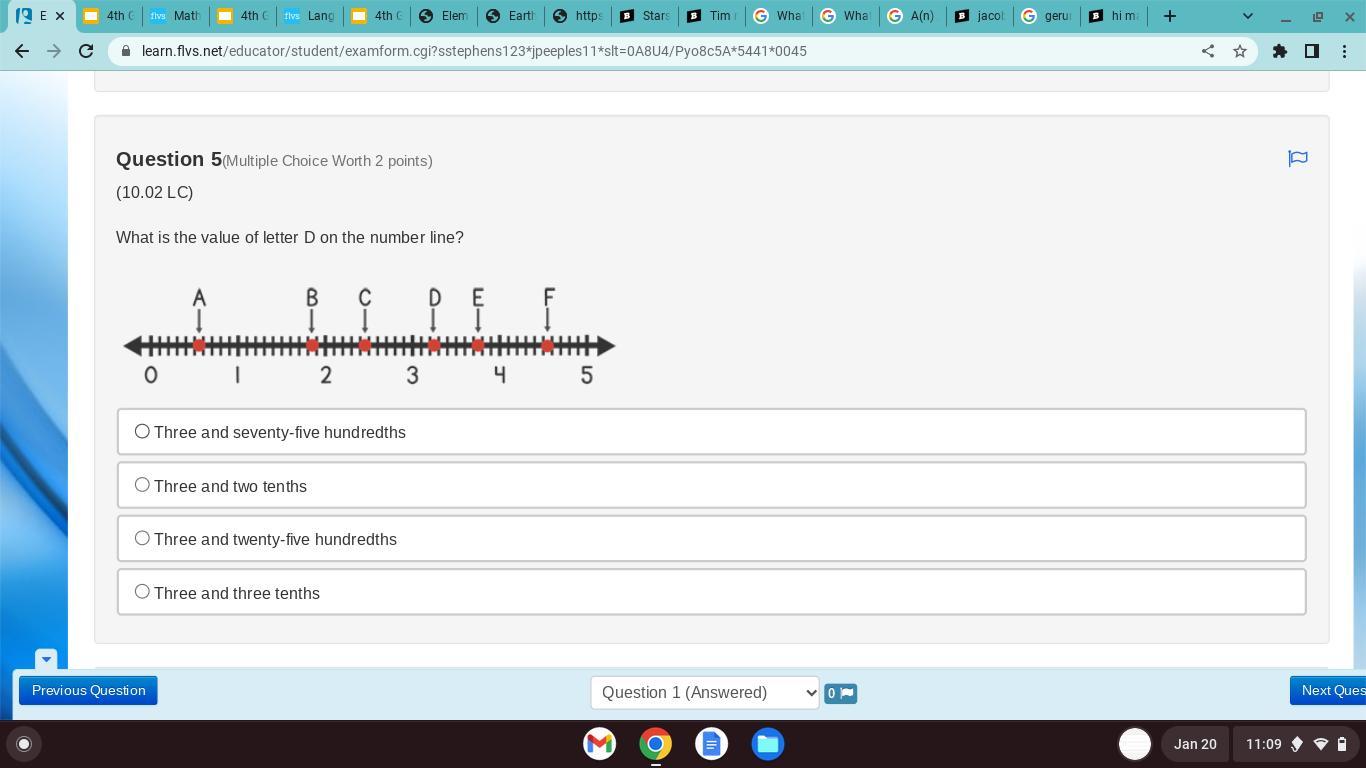
Answers
The exact value of the letter D is three and three-tenths.
What is a number line?A number line is a one-dimensional horizontal line where we can represent any real number. The origin of the number line is represented by zero left to it are all negative real numbers and right to it are all positive real numbers.
By observing the number line there are 10 subsections between two integers.
The letter D is in between two integers 3 and 4 so it can be from 3.1 to 3.9.
In between those ten subsections, the letter D is in the third subsection.
Therefore it is Three and three-tenths.
learn more about number line here :
https://brainly.com/question/13425491
#SPJ1
Please help!!!! 2 questions 50 points!!!!


Answers
Answer:
See below ~
Step-by-step explanation:
Question 1
The missing angles
Both the unknown angles have the same value as the other two angles in the triangles are the same∠(missing) = 180 - (72 x 2)∠(missing) = 180 - 144∠(missing) = 36°⇒ The sides are equal
⇒ Angles are not 90°
⇒ It is a rhombus
Question 2
The diagonals of the shape bisect other (Statement 1)NY = NW (given)XN = NZ (given)∠XNY = ∠WXZ (vertically opposite angles)ΔXNY ≅ ΔWXZ (SAS)They form two congruent triangles (Statement 2)From these two statements, it is evident the figure is a parallelogram13. Summerville has a population of 430,000
people, while Eagleton has a population of
5.7 x 105 people. What is the difference in
population between the two towns? Write your
answer in scientific notation.
Answers
Answer:
1.4 x 10 to the power of 5
Step-by-step explanation:
5.7 x 10 to the power of 5 = 570,000
570,000 - 430,000 = 140,000
1.4 x 10 to the power of 5 = 140,000
1.4 x 10 to the power of 5 is the answer
I need help in solving this, I dont want an answer. 10. The Wilson family had a family portrait framed for their living room. The frame measures 45 inches long and 37 inches wide. Which is a reasonable value for how much wall space the portrait will cover? A. B. 12 ft 12 ft C. 14 ft D. 14 ft?
Answers
Hope this helps!
A circle has a center at point A ( 3, − 1 ) and a point on the circle is located at R ( 5,4 ). What is the location of S, on the diameter RS?
Answers
A circle has a center at point A ( 3, − 1 ) and a point on the circle is located at R ( 5,4 ). The location of S is (1, -6).
To find the location of S on the diameter RS, we need to first find the midpoint of RS, which will be the center of the circle. Then we can find the coordinates of S by using the distance formula.
The midpoint of RS is the average of the coordinates of R and S:
((5 + x)/2, (4 + y)/2)
Since the midpoint is the center of the circle, it has the same coordinates as point A:
((5 + x)/2, (4 + y)/2) = (3, -1)
We can solve this system of equations for x and y:
(5 + x)/2 = 3
(4 + y)/2 = -1
Solving for x and y, we get:
x = 1
y = -6
Therefore, the location of S is (1, -6).
To know more about circle here
https://brainly.com/question/24375372
#SPJ4

V = (D*(A1 + A2 + (L1+L2) * (W1+W2)) /6)
Solve for D
Answers
Therefore, the required solution for D is:
\(D = \frac{6V}{(A1 + A2 + (L1 + L2) * (W1 + W2))}\)
To solve for D in the equation
\(V = \frac{(D * (A1 + A2 + (L1 + L2) * (W1 + W2))}{6}\)
We can follow these steps:
Multiply both sides of the equation by 6 to eliminate the denominator:
6V = D * (A₁ + A₂ + (L₁ + L₂) * (W₁ + W₂))
Divide both sides of the equation by (A₁ + A₂ + (L₁ + L₂) * (W₁ + W₂)):
\(\frac{6V}{(A_{1}+ A_{2} + (L_{1} + L_{2}) * (W_{1} + W_{2}))} = D\)
Therefore, the solution for D is:
\(D = \frac{6V}{(A1 + A2 + (L1 + L2) * (W1 + W2))}\)
Learn more about Solve:
https://brainly.com/question/28099315
#SPJ11
Calculate the double integral ∫∫ xy^2/ x^2+1 dA where the region of integration R= {(x,y)| 0 ≤ x ≤1, -3 ≤ y ≤ 3}
Answers
The value of the double integral ∫∫R (xy²) / (x² + 1) dA over the region R is 9 ln(2).
To calculate the double integral of the function f(x, y) = (xy²) / (x² + 1) over the region R = {(x, y) | 0 ≤ x ≤ 1, -3 ≤ y ≤ 3}, we can set up the integral as follows:
∫∫R (xy)² / (x² + 1) dA
First, we need to determine the order of integration. Since the limits of x are independent of y, we can integrate with respect to x first and then with respect to y.
∫∫R (xy²) / (x² + 1) dA = ∫ from y = -3 to 3 ∫ from x = 0 to 1 (xy²) / (x² + 1) dx dy
Now, let's evaluate the inner integral with respect to x:
∫ from x = 0 to 1 (xy²) / (x² + 1) dx
To simplify the integral, we can perform a u-substitution, letting u = x² + 1. Then du = 2x dx, and when x = 0, u = 1, and when x = 1, u = 2.
∫ (xy²) / (x² + 1) dx = (1/2) ∫ (y²) / u du
= (1/2) ∫ (y²) / u du
= (1/2) [y² ln(u)] | from 1 to 2
= (1/2) [y² ln(2) - y² ln(1)]
= (1/2) y² ln(2)
Now, we can integrate with respect to y:
∫ from y = -3 to 3 [(1/2) y² ln(2)] dy
= (1/2) ln(2) ∫ from y = -3 to 3 y² dy
= (1/2) ln(2) [ (1/3) y³ ] | from -3 to 3
= (1/2) ln(2) [ (1/3) (3³) - (1/3) (-3³) ]
= (1/2) ln(2) [ 9 - (-9) ]
= (1/2) ln(2) (18)
= 9 ln(2)
Therefore, the value of the double integral ∫∫R (xy²) / (x² + 1) dA over the region R is 9 ln(2).
To know more about integral check the below link:
https://brainly.com/question/27419605
#SPJ4
Scott drove 754 miles in 13 hours how many miles would he drive in 8 hours
Answers
You would divide 13 by 754=58
Then 58 times 8= 464
So 464 miles
Please help it’s with applying Rational numbers. First to answer is Brainliest!!!!!!!!
Donna is hanging a poster on her wall she wants to center it horizontally. The poster is 25 7/10 inches long, the space between the right edge of the poster and the right edge of the wall is 50 1/4 inches in the wall is 134 1/5 Inches long. Is the picture centered? Use the numbers given to find out, and use estimation to check if your answer is reasonable.
Answers
Answer:
The poster is not centered.Step-by-step explanation:
In the image attached you can observe a representation of this situation.
First, we need to transform each mixed number to a fraction.
\(25 \frac{7}{10}=\frac{257}{10}=25.70 \ in\)
\(50 \frac{1}{4} =\frac{201}{4} =50.25 \ in\)
\(134 \frac{1}{5} = \frac{671}{5} =134.20 \ in\)
Now, if the poster is centers, then the distance to the wall on the right and on the left, must be equal. We know that the space on the right is 50.25 inches. Then, we subtract to find the other side
\(134.20-50.25-25.70=58.25 \ in\)
So, the space in the left side of the poster is 58.25 inches long.
Therefore, the poster is not centered.

Tom's property has a shape of a parallelogram with the dimensions of l= x +75 and w= x + 45. If the perimeter is 300 feet, what is the value of x
Answers
Answer:
15 feets
Step-by-step explanation:
The perimeter of a parallelogram is given as :
P = 2(l + w)
l and w are the bases :
Substituting the values into the equation :
P = 2(x + 75 + x + 45)
P = 2(2x + 120)
P = 300
Hence ;
300 = 4x + 240
300 - 240 = 4x
60 = 4x
Divide both sides by 4 to isolate x
60 /4 = 4x / 4
15 = x
x = 15 feets
Frequency of a body is 60 Hz . What is its time period? (With explanation pls I’ll mark brainlist)
Answers
Answer:
0.016 s
Step-by-step explanation:
We know that
T = 1/f
Where
T = time period
f = frequency
T = 1/60
T = 0.016 s
Hence,
Time period is 0.016 s
\( \sf \: T= \frac{1}{F} \)
This is the basic formula, You can use this formula to solve similar problems. Remember that whenever Frequency is given and we have to find time period this formula will be applied!~
Time (T) = ?Frequency (F)=60Solution:\( \sf \: t = \frac{1}{60} \)
Convert the fraction to decimal\( \sf \: t = 0.16 \: \tt seconds\)
Please Explain:
For each pair of the following functions, fill in the correct asymptotic notation among Θ, o, and ω in statement f(n) ∈ ⊔(g(n)). Provide a brief justification of your answers
f(n) = n^3 (8 + 2 cos 2n) versus g(n) = n^2 + 2n^3 + 3n
Answers
The asymptotic notation relationship between the functions \(f(n) = n^3 (8 + 2 cos 2n)\) and \(g(n) = n^2 + 2n^3 + 3n\) is f(n) ∈ Θ(g(n)). Therefore, the growth rates of f(n) and g(n) are primarily determined by the cubic terms, and they grow at the same rate within a constant factor.
To determine the asymptotic notation relationship between the functions \(f(n) = n^3 (8 + 2 cos 2n)\) and \(g(n) = n^2 + 2n^3 + 3n\), we need to compare their growth rates as n approaches infinity.
Θ (Theta) Notation: f(n) ∈ Θ(g(n)) means that f(n) grows at the same rate as g(n) within a constant factor. In other words, there exists positive constants c1 and c2 such that c1 * g(n) ≤ f(n) ≤ c2 * g(n) for sufficiently large n.
o (Little-o) Notation: f(n) ∈ o(g(n)) means that f(n) grows strictly slower than g(n). In other words, for any positive constant c, there exists a positive constant n0 such that f(n) < c * g(n) for all n > n0.
ω (Omega) Notation: f(n) ∈ ω(g(n)) means that f(n) grows strictly faster than g(n). In other words, for any positive constant c, there exists a positive constant n0 such that f(n) > c * g(n) for all n > n0.
Now let's analyze the given functions:
\(f(n) = n^3 (8 + 2 cos 2n)\\g(n) = n^2 + 2n^3 + 3n\)
Since both functions have the same dominant term, we can say that f(n) ∈ Θ(g(n)) because they grow at the same rate within a constant factor. The other notations, o and ω, are not applicable here because neither function grows strictly faster nor slower than the other.
To know more about growth rate,
https://brainly.com/question/33562447
#SPJ11
utomobile trips there are major roads from city to city and major roads from city to city . how many different trips can be made from city to city passing through city ?
Answers
There are 8 different trips that can be made from City X to City Z, passing through City Y.
To find the number of different trips that can be made from City X to City Z, passing through City Y, we can use the multiplication principle of counting.
First, we need to choose one of the 2 major roads from City X to City Y. Then, for each of these roads, there are 4 major roads from City Y to City Z, and we need to choose one of these roads.
By the multiplication principle of counting, the total number of different trips from City X to City Z, passing through City Y, is the product of the number of choices at each stage. Thus, we get:
Number of different trips = Number of roads from City X to City Y x Number of roads from City Y to City Z
= 2 x 4
= 8
This calculation shows how the multiplication principle of counting can be used to find the total number of possible outcomes in a multi-stage process where the number of choices at each stage is known.
To learn more about outcomes click on,
https://brainly.com/question/14796795
#SPJ4
Complete question is:
Automobile Trips. There Are 2 Major Roads From City X To City Y And 4 Major Roads From City Y To City Z. How Many Different trips can be made from City X to City Z, passing through City Y?
(pythagorean theorem and the coordinate plane mc) determine the length of the line segment shown. line segment from negative 3 comma 10 to 4 comma negative 1 13 units 12 units 7 units 3 units
Answers
Using Pythagorean Theorem, the length of the line segment from (-3, 10) to (4, -1) is 13 units.
Pythagorean theorem describes the relationship between the sides of a right triangle. It states that the square of the hypotenuse is equal to the sum of the squares of the two other side.
c² = a² + b²
Let a = vertical distance between the two points
b = horizontal distance between the two points
c = distance between the two points / length of line segment
Hence, c² = (|y₂ - y₁|)² + (|x₂ - x₁|)².
Substitute the values of x and y and solve for c.
c² = (|y₂ - y₁|)² + (|x₂ - x₁|)²
c² = (|-1 - 10|)² + (|4 - -3|)²
c² = (|-11|)² + (|7|)²
c² = 11² + 7²
c² = 121 + 49
c² = 170
c = 13.04
length of line segment ≅ 13 units
Learn more about Pythagorean theorem here: brainly.com/question/9125970
#SPJ4

An automobile uses 17 gal of fuel to go 590 mi. how many gallons are required to travel 840 mi? (round your answer to one decimal place.)
Answers
Answer:
the car would use 49 gallons because you get a decimal of 49.49 so you would put got decimal to the nearest 1's place and that would be 49
How do you write 10 more than a number?
Answers
The algebraic expression for 10 more than a number is x + 10 or 10 + x.
The x in the expression is called a variable, which can be represented by any letter in the alphabet.
An algebraic expression is a mathematical expression that consists of numbers, variables and operators, and its value can change.
Some basic mathematical operators are +, -, x and /.
The given phrase states that a result can be obtained by adding 10 more to the variable.
The variable x can be replaced by any number.
If x equals 2, then the expression x + 10 has a value of 12.
To know more about algebraic expression visit brainly.com/question/953809
#SPJ4
Brendan says that the negative of - 1/3
is 3 because they are on opposite sides of zero when they are plotted on the number line.
Is Brendan correct? Explain your answer.
Answers
Answer:
No! Brendan has totally got the wrong idea.
Step-by-step explanation:
Numbers on the right hand side of zero are said to be positive, while, the numbers on the opposite side are said to be negative.
That means Brendan's correct in saying that -1/3 lies on the opposite side of 3, since negative numbers lie on the opposite side of the positives.
But,
Negative "of" a number is the same number with opposite sign.
That is, if a number is 3 units away from the zero, it's negative will also be 3 units away from zero, but on the opposite side.
-1/3 and 3 do not lie at the same distance from zero.
-1/3 would be approached before -1 by walking in the negative direction whereas 3 would be approached after 1.
Therefore, Brendan is wrong as the negative of a number has opposite sign but same "magnitude".
pls helpppp its nearly due and i need a solution AND a answer x

Answers
Answer:
Step-by-step explanation:
If ab is 4 times bc;
then ab= 4bc
ac= 5bc=75
bc= 75/5 = 15 cm
ab= (4*bc)
= 4 * 15 = 60
The probability of a student spending time reading is 0.59, and the probability of a student doing well on an exam and spending time reading is 0.58. What is the probability of a student doing well on an exam given that the student spends time reading
Answers
The probability of a student doing well on an exam given that they spend time reading is approximately 0.983 or 98.3%.
To calculate the probability of a student doing well on an exam given that the student spends time reading, we need to use conditional probability.
Let's denote:
P(R) as the probability of a student spending time reading (P(R) = 0.59),
P(E) as the probability of a student doing well on an exam (P(E)),
P(E|R) as the probability of a student doing well on an exam given that they spend time reading (P(E|R) = 0.58).
The formula for conditional probability is:
P(E|R) = P(E and R) / P(R).
Given that P(E and R) = 0.58 (the probability of a student doing well on an exam and spending time reading) and P(R) = 0.59 (the probability of a student spending time reading), we can substitute these values into the formula:
P(E|R) = 0.58 / 0.59 = 0.983.
Therefore, the probability of a student doing well on an exam given that the student spends time reading is approximately 0.983 or 98.3%.
To know more about probability, visit:
https://brainly.com/question/29120105
#SPJ11
pls help me asap
solve for x

Answers
Answer:
9
Step-by-step explanation:
You know AB=CB because all 3 arcs are equal, therefore:
5x + 8 = 53
5x = 53 - 8
5x = 45
x = 45/5 = 9
Lucy's house cost £200 000 at the start of 2014, the value of the house increased every year by 5%, work out the value of her house at start of 2017
Answers
Answer:
212000
Step-by-step explanation:
120000 - 5% = 190000
hence 5% is 10000
120000+ 30000= 212000
Find the rate of change (slope) given the set of data points below.
10, 19
4, 17
-2, 15
-8, 13
Answers
1/3 is the rate of change (slope) given the set of data points below
To find the rate of change (slope) given the set of data points, we can use the formula for slope:
slope = (change in y) / (change in x)
Using the given points:
Point 1: (10, 19)
Point 2: (4, 17)
Point 3: (-2, 15)
Point 4: (-8, 13)
We can calculate the slope between each pair of points:
Slope between Point 1 and Point 2:
slope = (17 - 19) / (4 - 10) = -2 / -6 = 1/3
Slope between Point 2 and Point 3:
slope = (15 - 17) / (-2 - 4) = -2 / -6 = 1/3
Slope between Point 3 and Point 4:
slope = (13 - 15) / (-8 - (-2)) = -2 / -6 = 1/3
The rate of change (slope) between these points is consistent and equal to 1/3.
Know more about slope here:
https://brainly.com/question/16949303
#SPJ8
Solve for m.
−16−m=29
Responses
m=13m is equal to 13
m=−13m is equal to negative 13
m=45m is equal to 45
m=−45m is equal to negative 45
Answers
The solution of the expression - 16 - m = 29 for the variable m is given as follows:
m = -45.
How to solve the expression for m?The expression in the context of this problem is defined as follows:
-16 - m = 29.
To solve for the variable m, the variable must be isolated, moving the term -16 to the right side, with the opposite sign, as follows:
- m = 29 + 16.
-m = 45.
(adding 29 and 16 = 45).
As the leading coefficient of m has a negative sign, the entire expression must be multiplied by -1, changing the sign of each term in the expression, hence the solution is given as follows:
m = -45.
This means that the fourth option, m = -45, among these given, is the correct option.
More can be learned about solutions of expressions at https://brainly.com/question/723406
#SPJ1
Pls help i need this today

Answers
a < 2
The point is open, it is located at the top of 2, and the arrow is directed to the left.
In the equation y = 1/2x + 3, when x is 2, what is y?
Answers
Answer:
I think when X is two Y is gonna be 4
Answer: y=4
Step-by-step explanation:
y=1/2 x 2+3
y=1/2x2 + 3 (cancel the 2's) if you want to check if is correct take your calculator and do: 1/2 X 2
y=1+3
y=4
-8 + x - 4 + 9x
Need help
Answers
Answer:
Step-by-step explanation:
-8+x-4+9x = -8-4+x+9x
= -12+10x
PLEASE MARK BRAINLIEST.