What is the y-intercept of the line 3x – 4y = 24?
Answers
Answer:
-4 becuase when you graph it the y intercepts at -4
Step-by-step explanation:
Answer:
y-intercept: (0,-6)
Step-by-step explanation:
To find the y-intercept of an equation you make x equal to 0 and we get the equation -4y=24 when we solve that equation by dividing by -4 from both sides and we get our y which is -6.
Hope this helps you :)
Related Questions
Factor 4xyz + 10x Please
Answers
Answer:2x(2yz + 5)
Step-by-step explanation:
The highest common factor if 4 and 10 is 2 and they have x in common
Fill in the blank. In the triangle below, y=
decimal places.
Round your answer to two
429
V
35
>
Answer here
SUBMIT

Answers
Answer:
47.10
Step-by-step explanation:
The mnemonic SOH CAH TOA reminds you that ...
... Cos = Adjacent/Hypotenuse
The value y is the length of the hypotenuse, and the given length 35 is the side adjacent to the given angle. Thus, the cosine relationship will be helpful.
Filling in the given values, we have ...
... cos(42°) = 35/y
Multiplying by y/cos(42°), we can find y to be ...
... y = 35/cos(42°) ≈ 35/0.7431
... y ≈ 47.10
Y will be approximately 47.10 in length
Step-by-step explanation:
we will use this form that we memorized in our schools ............. SOH CAH TOA
CAH means , Cos ∅= Adjacent/Hypotenuse
Given values
∅ =42°
hypotenuse= y
adjacent side length = 35
now putting in our values into
Cos ∅= Adjacent/Hypotenuse
OR
cos(42°) = 35/y
by multiplying y on both sides we get
y= 35/cos( 42°)
cos(42°)= 0.743
so y= 35/0.743
y = 47.10632
OR
y ≈ 47.10
The subtotal for a TV was $1,029.99. What does that mean?
Answers
if x is a continuous random variable with the uniform distribution u(5.5,20.5), what is p(x<8)?
Answers
The correct value of p(x<8) is 1.875.
Define probabilityTo determine how probable something is gonna occur, use probability. It is a number between 0 and 1, where 0 denotes the absence of a possibility and 1 denotes the existence of one. By dividing the number of favorable outcomes by the entire number of potential possibilities, the probability of an occurrence is determined.
To find the probability that is greater than 8, we need to integrate this probability density function from 5.5 to 20.5:
P(X < 8) = ∫[5.5,20.5] f(x) dx
= ∫[5.5,20.5] (1/8) dx
= [x/8] from 5.5 to 20.5
= (20.5/8) - (5.5/8)
= 15/8
= 1.875.
Therefore, the correct probability is 1.875.
Learn more about probability here:
https://brainly.com/question/31391749
#SPJ4
(How many terms are needed in the series for cosx to compute the value of cosx for |x | ≤ 1/1/12 accurate to 12 decimal places (rounded)? Name the theorem you are using to get to the solution. (4+1)
Answers
The value of cos(x) for |x| ≤ 1/12 accurate to 12 decimal places (rounded), we need at least 5 terms in the series of cos(x). We will use Taylor's theorem to derive this result.
Taylor's theorem, also known as the Taylor series theorem, is a mathematical formula used to represent functions as a sum of infinitely many derivatives in order to approximate them over a certain interval.
This formula allows us to derive the value of a function at a point using information about its derivatives at that point.
In essence, Taylor's theorem is a tool used in calculus to model complex functions that cannot be easily solved.
Using Taylor's theorem to solve the question:
We know that the Taylor series expansion of cos(x) is given by the formula:
cos(x) = 1 - x²/2! + x⁴/4! - x⁶/6! + ...
To get an accurate value of cos(x), we need to keep adding terms in the series until the absolute value of the next term is less than our required accuracy.
Using |x| ≤ 1/12 and rounding to 12 decimal places, we have an error tolerance of 0.000000000001.
Therefore, we need to find the smallest value of n such that \(|x^(n+1)/(n+1)!| ≤ 0.000000000001,\)
where x = 1/12.
Substituting x = 1/12,
we have |(1/12)^(n+1)/(n+1)!| ≤ 0.000000000001
Using a calculator, we can find that n = 4 satisfies this inequality.
Therefore, we need at least 5 terms in the series of cos(x) to compute the value of cos(x) for |x| ≤ 1/12 accurate to 12 decimal places (rounded).
Conclusion:
To calculate the value of cos(x) for |x| ≤ 1/12 accurate to 12 decimal places (rounded), we need at least 5 terms in the series of cos(x). We used Taylor's theorem to derive this result.
To know more about Taylor's theorem visit
https://brainly.com/question/13264870
#SPJ11
"Here are some values of sequence D"
n | D(n)
1 | 13
5 | 7
7 | 4
A) "Write a recursive definition for the sequence"
B) "Write a definition for this sequence for the nth term"
Answers
Answer:
See below
Step-by-step explanation:
A) Recursive Definition
The value of each term in a sequence that starts at 13 is reduced by 1.5 for each step in the sequence.
B) Definition for nth Term
D(n) = D(1)+(n-1)(-1.5)
D(1) = 13
D(n) = 13+(n-1)(-1.5)
Examples:
D(5) = 13 + (5-1)*(-1.5)
D(5) = 13 + (4)*(-1.5)
D(5) = 13 - 6, or 7
------------------
D(7) = 13 + (7-1)*(-1.5)
D(7) = 13 + (6)*(-1.5)
D(7) = 4
16 308/1000 as a decimal
Answers
Answer: 16.308
Step-by-step explanation:brainiest please
Please answer this for me
A
B
C
D
E

Answers
Answer:
D
Step-by-step explanation:
The range of a set of numbers is
range = largest number - smallest number , then
range = 25 - 6 = 19 → D
Which graph represents the solution set for the compound inequality below? ---x+ 10 ≥7 X-10≥7
x-10≥7
Answers
A graph which represents the solution set for the compound inequality is shown in the image attached below.
How to determine the graph?In order to determine the graph which represents the solution set for the compound inequality, we would evaluate the given inequalities as follows.
Given the following inequalities:
⅓x + 10 ≥ 7
x - 10 ≥ 7
For the first inequality, we have:
⅓x + 10 ≥ 7
Multiply all through by 3;
x + 30 ≥ 21
x ≥ 21 - 30
x ≥ -9 ⇒ x < 9.
For the first inequality, we have:
x - 10 ≥ 7
x ≥ 7 + 10
x ≥ 17.
In conclusion, a graph which represents the solution set for the compound inequality is shown by using the number line in the image attached below.
Read more on inequalities here: https://brainly.com/question/24372553
#SPJ1

the incomes in a certain larger population of college teachers have a normal distribution with mean of $60,000 and standard deviation of $5,000. four teachers are selected at random from this population to serve on a salary review committee. what is the probability that their average salary exceeds $65,000.
Answers
If the incomes in a certain larger population of college teachers have a normal distribution with mean of $60,000 and standard deviation of $5,000.the probability that their average salary exceeds $65,000 is 0.0228.
What is probability?Probability is the tendency or likelihood that an event will happen.
First step is to find the standard deviation
Standard deviation= $5,000/√4
Standard deviation= $5,000/2
Standard deviation= $2,500
Second step is to find the z -score
Z= 65,000 - 60,000/2500
Z= 5,000/2500
Z= 2
Now let find the pvalue of 2
pvalue of 2 = 0.0228
Therefore the probability is 0.0228.
Learn more about probability here:https://brainly.com/question/15047130
#SPJ1
tamika selects two different numbers at random from the set and adds them. carlos takes two different numbers at random from the set and multiplies them. what is the probability that tamika's result is greater than carlos' result?
Answers
If Tamika adds two separate numbers at random from the collection, the likelihood that her result will be higher than Carlos' result is 4/9. To multiply two random integers from the set, Carlos chooses two more random numbers.
what is probability ?This event has a chance of happening or not happening.
calculation
Tamika might receive any of the following results, all of which are equally likely:
8+9=17
8+10=18
9+10=19
The various potential values that Carlos could receive—all equally likely—are:
3 * 5=15
3 * 6=18
5 * 6=30
Because 17 is only greater than 15, the likelihood that Tamika's total would be greater than Carlos's set is 1/3.
Because 18 is only greater than 15, the likelihood that Tamika's total would be greater than Carlos's set is 1/3.
Due to the fact that 19 is greater than both 15 and 18, the likelihood that Tamika's total would be greater than Carlos's set is 2/3.
We have 1/3(1/3+1/3+2/3)=1/3(4/3)=4/9 since each sum has a 1/3 chance of being chosen.
the likelihood of the difference between Tamika's performance and Carlos' performance is 4/9.
To know more about probability visit :-
https://brainly.com/question/30034780
#SPJ4
You have a bag of poker chips, containing 2 white, 1 red, and 3 blue chips. White chips are worth $1, red chips are worth $3 and blue chips are worth $5. You need $7 worth of chips in order to see someone’s raise, so you take chips out of the bag one at a time, noting the color of each one as it’s removed, and stop when the total value of the chips removed is at least $7. How many sequences of chip colors are possible when you do this?
Answers
There are 144 possible sequences of chip colors.
How many sequences of chip colors are possibleWe can solve this problem by counting the number of possible sequences of chip colors that can be drawn from the bag until the total value of the chips is at least $7.
Let's consider all the possible sequences of chips that can be drawn from the bag. The first chip can be any of the 6 chips in the bag. For each chip color, there are different scenarios that can happen after drawing the first chip:
If the first chip is a white chip, then we need to draw chips worth $6 more in order to reach $7. We can draw any combination of the remaining 5 chips to get a total value of $6 or more. There are 2 white, 1 red, and 3 blue chips remaining, so there are 2^5 = 32 possible combinations.If the first chip is a red chip, then we need to draw chips worth $4 more in order to reach $7. We can draw any combination of the remaining 5 chips to get a total value of $4 or more. There are 2 white, 1 red, and 3 blue chips remaining, so there are 2^5 = 32 possible combinations.If the first chip is a blue chip, then we need to draw chips worth $2 more in order to reach $7. We can draw any combination of the remaining 5 chips to get a total value of $2 or more. There are 2 white, 1 red, and 2 blue chips remaining, so there are 2^4 = 16 possible combinations.Therefore, the total number of possible sequences of chip colors that can be drawn from the bag until the total value of the chips is at least $7 is: 2 x 32 + 1 x 32 + 3 x 16 = 144
Learn more on sequence here;
https://brainly.com/question/6561461
#SPJ1
What must a presentation contain to be called a multimedia presentation?
Answers
Answer:
It must include many types of media such as different social media websites.
Step-by-step explanation:
Find the area of the figure.

Answers
Step-by-step explanation:
such problems are always the combination of areas of simple figures.
in our case here the simplest way seems to me to calculate the area of the whole 15×15 square (the side lengths are 15 and 9+6 = 15) and then subtract the small 6×6 square (top left), the small 6×3 triangle (bottom right) and the larger 6×9 triangle (top right).
we know that the left side of the main square is 9+6 = 15.
we know that the missing side piece (top right) is also 6 (like its left side). and the right side piece is 15-6-6 = 3.
that is how we know the side lengths of the missing pieces.
so,
15×15 = 225 cm²
the small square is
6×6 = 36 cm²
the large triangle is
6×9/2 = 3×9 = 27 cm²
the small triangle is
6×3/2 = 3×3 = 9 cm²
so, the total area of the figure is
225 - 36 - 27 - 9 = 153 cm²
Please i need help pic included

Answers
Answer:
They using an Algebra calculator on your chromebook :)

Answer:
Slope: -3
y-intercept: 5
x | y
0 | 5
5/3 | 0
A teacher working's day is 7 1/2 hours long. one certain day, he spent 3 1/2 hours teaching and 2 1/2 hours marking student assignment. What fraction did he spend (a) Teaching (b) Marking.
Answers
Answer:
(a) 7/15
(b) 1/3
Step-by-step explanation:
(a) teaching:
(3 1/2) / (7 1/2) = (7/2) / (15/2) = 7/2 * 2/15 = 7/15
(b) marking:
(2 1/2) / (7 1/2) = (5/2) / (15/2) = 5/2 * 2/15 = 5/15 = 1/3
Use Lagrange multipliers to find the distance from the point (2, 0, −1) to the plane 8x - 4y + 9z+ 1 = 0.
Answers
We are given a point (2, 0, -1) and a plane 8x - 4y + 9z + 1 = 0. We need to find the distance from the point to the plane using Lagrange multipliers.
To find the distance from a point to a plane using Lagrange multipliers, we need to set up an optimization problem with a constraint equation representing the equation of the plane.
Let's denote the distance from the point (2, 0, -1) to a general point (x, y, z) on the plane as D. We want to minimize D subject to the constraint equation 8x - 4y + 9z + 1 = 0.
To set up the Lagrange multiplier problem, we define a function f(x, y, z) = (x - 2)² + y² + (z + 1)² as the square of the distance. We also introduce a Lagrange multiplier λ to account for the constraint.
Next, we form the Lagrangian function L(x, y, z, λ) = f(x, y, z) - λ(8x - 4y + 9z + 1). We then find the partial derivatives of L with respect to x, y, z, and λ, and set them equal to zero.
By solving the resulting system of equations, we can find the values of x, y, and z that minimize the distance. Finally, we substitute these values into the distance formula D = √((x - 2)² + y² + (z + 1)²) to obtain the minimum distance.
To know more about Lagrange multipliers click here: brainly.com/question/30776684
#SPJ11
find all points at which the direction of fastest change of the function f(x, y) = x2 y2 − 6x − 8y is i j. (enter your answer as an equation.)
Answers
The required equation is \(x^2y^4 + 4x^3y^3 - 4x^2y^2 - 12x^2y\) + 25 = 0
How to find points at which the direction of fastest change of the function?The direction of fastest change of a function at a point is given by the gradient of the function at that point. Therefore, to find the points at which the direction of fastest change of the function f(x, y) = \(x^2 y^2\) − 6x − 8y is in the direction of the vector i j, we need to find the gradient of f(x, y) and then find the points where the gradient is parallel to the vector i j.
The gradient of f(x, y) is given by:
∇f(x, y) = <∂f/∂x, ∂f/∂y> =\(< 2xy^2 - 6, 2x^2y - 8 >\)
To find the points at which the direction of fastest change is in the direction of i j, we need to find the points where the gradient is parallel to i j. This means that the dot product of the gradient and i j should be equal to the product of their magnitudes:
∇f(x, y) · i j = ||∇f(x, y)|| ||i j||
Substituting the values, we get:
\((2xy^2 - 6, 2x^2y - 8)\)· (1, 0) = sqrt((\(2xy^2 - 6)^2 + (2x^2y - 8)^2\)) * sqrt(\(1^2 + 0^2\))
Simplifying this equation, we get:
\(2xy^2\)- 6 = sqrt((\(2xy^2 - 6)^2\) + (\(2x^2y - 8)^2\))
Squaring both sides and simplifying, we get:
\(x^2y^4 + 4x^3y^3 - 4x^2y^2 - 12x^2y + 25 = 0\)
Therefore, the points at which the direction of fastest change of f(x, y) is in the direction of i j are given by the solution of the quartic equation above.
Learn more about direction of fastest change
brainly.com/question/17055351
#SPJ11
Gary drew a rectangle with a perimeter of 16 inches. Then he tried to draw a square with a perimeter of 16 inches.
Select the dimensions of the rectangle drawing.
16 inches by 7 inches 1 inch by 7 inches
16 inches by 1 inch7 inches by 4 inches
Select the dimensions of the square drawing.
1 inch by 1 inch
4 inches by 4 inches
16 inches by 16 inches
7 inches by 7 inches
Answers
Answer: I think u have to multiply all da numbers.
Step-by-step explanation:
Answer:
ooofffffffff
Step-by-step explanation:
The cost of tickets of a comedy show is Rs 700 for adult and Rs 500 for child . If family paid Rs 3100 for 5 tickets , how many tickets were purchased in each category?
Answers
Answer:
Cost of an adult =700
Cost of a child =500
Family paid=3100
They got 5 tickets
So,
700x+500y=3100
x+y=5
Multiplying 2nd equation to x=5-y
700(5-y)+500y=3100
y=2
x=5-2
=3
so u got the answer
If a sample includes three individuals with scores of 4, 6, and 8, the estimated population variance is 1) (2 + 0 + 2) / 2 = 2 2) (4 + 0 + 4) / 3 = 2.67 3) (2 + 0 + 2)/3 = 1.33 6 4) (4 + 0 + 4) / 2 - 4
Answers
If a sample includes three individuals with scores of 4, 6, and 8, the estimated population variance is (4 + 0 + 4) / 2 - 4. So, correct option is 4.
The estimated population variance formula is the sum of squared deviations from the mean divided by the degrees of freedom. In this case, the degrees of freedom would be n-1, where n is the sample size.
Using the given sample of 4, 6, and 8, we can calculate the sample mean as (4+6+8)/3 = 6.
Then, we calculate the deviations from the mean for each score:
4 - 6 = -2
6 - 6 = 0
8 - 6 = 2
We square each deviation to get 4, 0, and 4. Then, we sum the squared deviations: 4 + 0 + 4 = 8.
Since there are three scores in the sample, the degrees of freedom is 3 - 1 = 2.
Finally, we divide the sum of squared deviations by the degrees of freedom to get the estimated population variance: 8/2 = 4.
Therefore, option 4) (4 + 0 + 4) / 2 = 4 is the correct answer.
To learn more about sample click on,
https://brainly.com/question/28920592
#SPJ4
Let D be a region bounded by a simple closed path C in the xy-plane. The coordinates of the centroid (xˉ,yˉ) of D are xˉ=2A1∮Cx2dyyˉ=−2A1∮Cy2dx where A is the area of D. Find the centroid of a quarter-circular region of radius a. (xˉ,yˉ)=___
Answers
The centroid of a quarter-circular region of radius $a$ is $\left(\frac{a^2}{2\pi}, \frac{a^2}{4}\right)$.
The centroid of a region is the point that is the average of all the points in the region. It can be found using the following formulas: xˉ=2A1∮Cx2dyyˉ=−2A1∮Cy2dx
where $A$ is the area of the region, $C$ is the boundary of the region, and $x$ and $y$ are the coordinates of a point in the region.
For a quarter-circular region of radius $a$, the area is $\frac{a^2\pi}{4}$. The integrals in the formulas for the centroid can be evaluated using the following substitutions:
x = a \cos θ
y = a \sin θ
where $θ$ is the angle between the positive $x$-axis and the line segment from the origin to the point $(x,y)$.
After the integrals are evaluated, we get the following expressions for the centroid:
xˉ=a22π
yˉ=a24
Therefore, the centroid of a quarter-circular region of radius $a$ is $\left(\frac{a^2}{2\pi}, \frac{a^2}{4}\right)$.
The first step is to evaluate the integrals in the formulas for the centroid. We can do this using the substitutions $x = a \cos θ$ and $y = a \sin θ$.
The integral for $xˉ$ is:
xˉ=2A1∮Cx2dy=2A1∮Ca2cos2θdy
We can evaluate this integral by using the double angle formula for cosine: cos2θ=12(1+cos2θ)
This gives us: xˉ=2A1∮Ca2(1+cos2θ)dy=2A1∮Ca2+a2cos2θdy
The integral for $yˉ$ is:
yˉ=−2A1∮Cy2dx=−2A1∮Ca2sin2θdx
We can evaluate this integral by using the double angle formula for sine:
sin2θ=2sinθcosθ
This gives us:
yˉ=−2A1∮Ca2(2sinθcosθ)dx=−2A1∮Ca2sin2θdx
The integrals for $xˉ$ and $yˉ$ can be evaluated using the trigonometric identities and the fact that the area of the quarter-circle is $\frac{a^2\pi}{4}$.
After the integrals are evaluated, we get the following expressions for the centroid:
xˉ=a22π
yˉ=a24
Therefore, the centroid of a quarter-circular region of radius $a$ is $\left(\frac{a^2}{2\pi}, \frac{a^2}{4}\right)$.
To know more about radius click here
brainly.com/question/29082108
#SPJ11
quel est le prix d'une PlayStation a 395 euro qui bénéficie d'une réduction de 18 pourcent
Answers
Answer:
323.9
Step-by-step explanation:
395/100 = 3.95 (this is each unit of the price)
3.95 x 18 = 71.1
395 - 71.1 = 323.9
Solve the following systems of equations using Gaussian Elimination. 2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Find the inner product of two vectors A = (2, -3,0) and B = = (-1,0,5)
Answers
The inner product of two vectors A = (2, -3,0) and B = (-1,0,5) is -2 / √(13×26).
Solving the given system of equations using Gaussian elimination:
2x + 3y + z = 2 y + 5z = 20 -x+2y+3z = 13
Matrix form of the system is
[A] = [B] 2 3 1 | 2 0 5 | 20 -1 2 3 | 13
Divide row 1 by 2 and replace row 1 by the new row 1: 1 3/2 1/2 | 1
Divide row 2 by 5 and replace row 2 by the new row 2: 0 1 1 | 4
Divide row 3 by -1 and replace row 3 by the new row 3: 0 0 1 | 5
Back substitution, replace z = 5 into second equation to solve for y, y + 5(5) = 20 y = -5
Back substitution, replace z = 5 and y = -5 into the first equation to solve for x, 2x + 3(-5) + 5 = 2 2x - 15 + 5 = 2 2x = 12 x = 6
The solution is (x,y,z) = (6,-5,5)
Therefore, the solution to the given system of equations using Gaussian elimination is (x,y,z) = (6,-5,5).
The given two vectors are A = (2, -3,0) and B = = (-1,0,5). The inner product of two vectors A and B is given by
A·B = |A||B|cosθ
Given,A = (2, -3,0) and B = (-1,0,5)
Magnitude of A is |A| = √(2²+(-3)²+0²) = √13
Magnitude of B is |B| = √((-1)²+0²+5²) = √26
Dot product of A and B is A·B = 2(-1) + (-3)(0) + 0(5) = -2
Cosine of the angle between A and B is
cosθ = A·B / (|A||B|)
cosθ = -2 / (√13×√26)
cosθ = -2 / √(13×26)
Learn more about equation at
https://brainly.com/question/12998758
#SPJ11
I NEED HELP ASAP ! THIS IS FOR A PAST DUE QUIZ. THEY ARE GIVING ME ONE MORE CHANCE
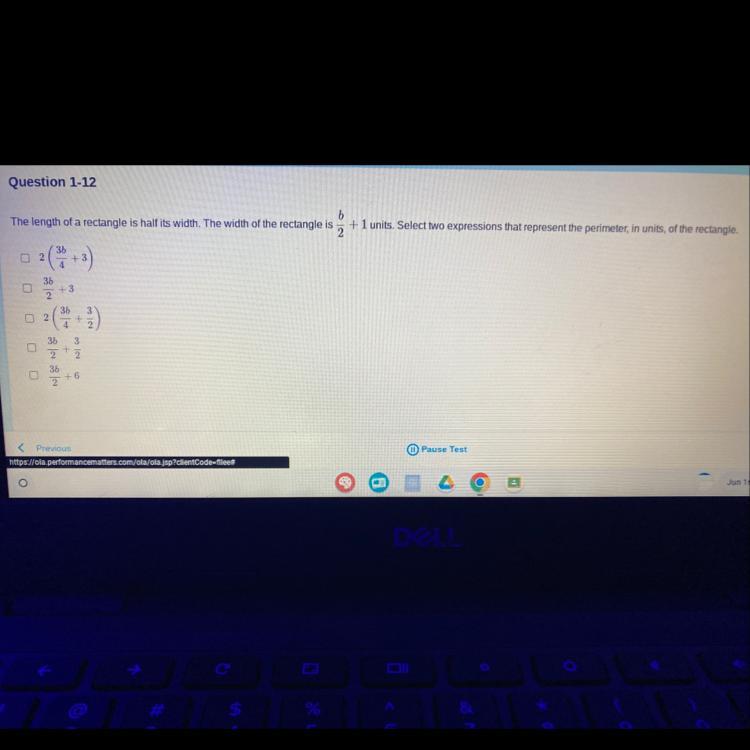
Answers
Answer:
3b/2 + 3
Step-by-step explanation:
The formula to calculate perimeter of rectangle is 2l + 2w
The length is half the width so length is 1/2 (b/2 +1), which when simplified is b/4 + 1/2
Using the formula to calculate perimeter you can substitute and calculate
p= 2l + 2w
p= 2(b/4 + 1/2) + 2(b/2 + 1)
p= 2b/4 +2/2 + 2b/2 +2
p= 1/2b + 1 + b + 2
p= 3/2b + 3
Simplified it's 3b/2 +3
6 less than 3 times a number 42 what is the number
Answers
Answer: -120
6 less than is 6 - and 3 times a number 42 is 3 x 42 so...
6 - (3 x 42) = -120
3
87. 8
98
-
8[?].
the question didn’t have enough letters for me to post so i’m using this to post it
![387. 898-8[?]. the question didnt have enough letters for me to post so im using this to post it](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/lLuzZ1uhD8L8HLJFEZFOl86olbFs974V.png)
Answers
8(8)^3
Solution
8^4
Insert 4 in the green box
Given h(a) = 5x – 2. find h(5)
Answers
Answer:
23
Step-by-step explanation:
h(a) = 5x-2
h(5) = 5(5)-2
h(5) = 25-2
h(5) = 23
Answer:
23
Step-by-step explanation:
Plug in 5 as x
h(x) = 5x - 2
h(5) = 5(5) - 2
h(5) = 25 - 2
h(5) = 23
So, h(5) = 23
Express this number in scientific notation. 0.0062
Answers
This number in scientific notation is 6.2 x 10^-3
How to express this number in scientific notation?The number is given as
0.0062
Multiply by 1
So, we have
0.0062 = 0.0062 * 1
Express 1 as 1000/1000
So, we have
0.0062 = 0.0062 * 1000/1000
This gives
0.0062 = 6.2/1000
This gives
0.0062 = 6.2/10^3
Rewrite as
0.0062 = 6.2 x 10^-3
Hence, this number in scientific notation is 6.2 x 10^-3
Read more about scientific notation at
https://brainly.com/question/5756316
#SPJ1
Which is more, 662 feet or
1
8
of a mile?
Answers
Answer:
the answer is 662 feet
Step-by-step explanation:
becuase one eighth of a mile is 660 feet