Which is not the rule of similarity :- AAA SSS RHS SAS?
Answers
The rule of similarity that is not included in the given list is "RHS," which stands for "Right Angle, Hypotenuse, Side."
This rule states that if a right triangle has a hypotenuse and one side that are congruent to the hypotenuse and one side of another right triangle, respectively, then the two triangles are similar.
The other three rules of similarity that are listed in your question are:
AAA (Angle-Angle-Angle): If two triangles have corresponding angles that are congruent, then the triangles are similar.SSS (Side-Side-Side): If two triangles have corresponding sides that are in the same proportion, then the triangles are similar.SAS (Side-Angle-Side): If two triangles have two sides that are in the same proportion and the included angle is congruent, then the triangles are similar.To learn more about the triangles, visit:
brainly.com/question/2773823
#SPJ4
Related Questions
what 27 over 54 in lowest terms
Answers
Answer: 1/2
Step-by-step explanation: Divide both the numerator and denominator by the GCD (Greatest Common Denominator)
27 ÷ 27
54 ÷ 27 (its 27/54 divided by 27/27
Reduced fraction:
1/2
Therefore, 27/54 simplified to lowest terms is 1/2.
Hunter misses 10% of the free throws he attempts in a season. How many total free throws did he attempt if he missed 54?
Answers
Answer:
540
Step-by-step explanation:
If you divide 540 by 100 (100%) you get 5.4 then multiply it by 10 (10%) to get 54 again. THIS WAS TO CHECK TO GET: 10% or 100% is 10 so multiply 54•10=540
Hope this helps! ;-)
Let g : Z x Z -> Z be defined by g(m,n) = 6m+3n. is the function g an injection? is the function g a surjection? justify your conclusions.
Answers
The function g : Z x Z -> Z defined by g(m,n) = 6m+3n is not an injection, but it is a surjection. This means that g is not a one-to-one function, but it does cover every element in the codomain.
To determine if the function g : Z x Z -> Z defined by g(m,n) = 6m+3n is an injection, we need to verify whether distinct inputs result in distinct outputs. Suppose g(m1, n1) = g(m2, n2) for some (m1, n1), (m2, n2) in Z x Z. Then, 6m1 + 3n1 = 6m2 + 3n2, which can be simplified to 2m1 + n1 = 2m2 + n2. Thus, m1 - m2 = (n2 - n1)/2. Since m1, m2, n1, and n2 are integers, (n2 - n1)/2 must also be an integer. Therefore, n2 - n1 must be even. It follows that if g(m1, n1) = g(m2, n2), then either m1 = m2 and n1 = n2 or m1 - m2 is odd. Hence, g is not an injection.
To determine if g is a surjection, we need to verify whether every integer in the codomain Z is mapped to by some element in the domain Z x Z. Given any integer z in Z, let m = 0 and n = (z/3). Then, g(m, n) = 6m + 3n = 3z, which means that g is a surjection.
For more about surjection;
https://brainly.com/question/29738050
#SPJ11
Can u help with my homework
;-;

Answers
Answer:
id sa mp be para sure win ta
What is the product of 2x3 +9 and x3 +7?
Answers
The product of the expression is 2x⁶ + 23x³ + 63
How to determine the productFirst, we should note that algebraic expressions are described as expressions that are composed of coefficients, terms, constants, variables and factors.
These algebraic expressions are also made up of mathematical operations, such as;
BracketAdditionMultiplicationDivisionParenthesesSubtractionFrom the information given, we have that;
2x3 +9 and x3 +7?
Then,
(2x³ + 9)(x³ + 7)
expand the bracket
2x⁶ + 14x³ + 9x³ + 63
add like terms
2x⁶ + 23x³ + 63
Learn about algebraic expressions at: https://brainly.com/question/4344214
#SPJ1
A deck of playing cards has four suits, with thirteen cards in each suit consisting of the numbers 2 through 10, a jack, a queen, a king, and an ace. The four suits are hearts, diamonds, spades, and clubs. A hand of five cards will be chosen at random. Which statement is true?
Answers
Answer:
Step-by-step explanation:
Which statements are true? Check all that apply.
The total possible outcomes can be found using 52C5.
The total possible outcomes can be found using 52P5.
The probability of choosing two diamonds and three hearts is 0.089.
The probability of choosing five spades is roughly 0.05
The probability of choosing five clubs is roughly 0.0005.
Since it can be chosen in any order, we use combination and not permutation. The number of ways of choosing 5 cards from a group of 52 cards is 52C5.
The probability of choosing two diamonds and three hearts = \(\frac{^{13}C_2*^{13}C_3}{^{52}C_5} = 0.0086\) so the third one is not true.
The probability of choosing five spades = \(\frac{^{13}C_5}{^{52}C_5}\) ≈ 0.0005. The fourth statement is not true
The probability of choosing five clubs = \(\frac{^{13}C_5}{^{52}C_5}\) ≈ 0.0005, the fifth one is.
So the answer is the first and fifth statement.
The probability of selecting a combination of cards is given by the ratio of
the ways of selecting the cards to the number of possible outcomes.
The true statements are;
The total number possible outcomes is ₅₂C₅.The probability of choosing five clubs is roughly 0.0005.Reasons:
First statement;
Number of cards in the deck of playing cards = 52
The number of possible outcome is given by the combinations of 5 that can be chosen from 52, as follows;
\(\displaystyle The \ \mathbf{number} \ of \ \mathbf{possible \ outcomes}} = _{52}C_5 = \frac{52!}{5! \cdot (52 - 5)!} = 2598960\)
Therefore;
The statement; the total number possible outcomes is ₅₂C₅ is trueThird statement;
The number of ways of choosing two diamonds is found as follows;
\(\displaystyle Choosing \ two \ diamonds = _{13}C_2 = \mathbf{\frac{13!}{2! \cdot (13 - 2)!}} = 78\)
The number of ways of choosing three hearts is found as follows;
\(\displaystyle Choosing \ three \ hearts = _{13}C_3 = \frac{13!}{3! \cdot (13 - 3)!} = 286\)
The number of ways of choosing two diamonds and three hearts is found as follows;
\(\displaystyle Choosing \ two \ diamonds \ and \ three \ hearts = \frac{_{13}C_2 \times _{13}C_3}{_{52}C_5} = 0.00858\)
Therefore, the number of ways of choosing two diamonds and three hearts ≠ 0.089
\(\displaystyle Choosing \ two \ diamonds \ and \ three \ hearts = \mathbf{\frac{_{13}C_2 \times _{13}C_3}{_{52}C_5}} \neq 0.089\)
Fourth statement;
\(\displaystyle Probability \ of \ choosing \ five \ spades = \frac{_{13}C_5 }{_{52}C_5} \approx 0.0005\)
Therefore;
\(\displaystyle Probability \ of \ choosing \ five \ spades = \mathbf{\frac{_{13}C_5 }{_{52}C_5}} \neq 0.05\)
Fifth statement;
\(\displaystyle Probability \ of \ choosing \ five \ clubs= \frac{_{13}C_5 }{_{52}C_5} \approx 0.0005\)
Therefore;
The statement, the probability of choosing five clubs is roughly 0.0005 is true.The possible question options in the question are;
The total possible outcomes is given by ₅₂C₅
The total possible outcomes is given by ₅₂P₅
Probability of choosing 3 hearts and 2 diamonds is 0.089
The likelihood of choosing 5 spades is approximately 0.05
The likelihood of choosing 5 clubs is approximately 0.0005
Learn more about combinations and probability here:
https://brainly.com/question/25718474
for the function f whose graph is given below, list the following quantities in increasing order, from smallest to largest. a: ∫08f(x)dxb: ∫58f(x)dxc: ∫48f(x)dxd: ∫04f(x)dx
Answers
To answer this question, we need to consider the area under the graph of the function f for different intervals. Let's look at each interval separately:
a) ∫0 to 8 f(x) dx: This integral represents the area under the graph of f from x = 0 to x = 8. From the graph, we can see that the area under the curve for this interval is negative, since the curve is below the x-axis. Therefore, the value of this integral is negative.
b) ∫5 to 8 f(x) dx: This integral represents the area under the graph of f from x = 5 to x = 8. From the graph, we can see that the area under the curve for this interval is positive, since the curve is above the x-axis. Therefore, the value of this integral is positive.
c) ∫4 to 8 f(x) dx: This integral represents the area under the graph of f from x = 4 to x = 8. From the graph, we can see that the area under the curve for this interval is greater than the area under the curve for interval b, since the curve is higher above the x-axis. Therefore, the value of this integral is greater than the value of integral b.
d) ∫0 to 4 f(x) dx: This integral represents the area under the graph of f from x = 0 to x = 4. From the graph, we can see that the area under the curve for this interval is greater than the area under the curve for interval a, since the curve is higher above the x-axis. Therefore, the value of this integral is greater than the value of integral a.
Therefore, the quantities listed in increasing order from smallest to largest are:
a) ∫0 to 8 f(x) dx (negative)
b) ∫5 to 8 f(x) dx (positive)
c) ∫4 to 8 f(x) dx (greater than b)
d) ∫0 to 4 f(x) dx (greater than a)
In summary, the area under the graph of a function can be used to compare integrals for different intervals. By analyzing the graph and determining the sign and magnitude of the area under the curve for each interval, we can list the integrals in increasing or decreasing order.
a) \(\int\limits^8_0 {f(x)} \, dx\), the value of this integral is negative.
b) \(\int\limits^8_5 {f(x)} \, dx\), the value of this integral is positive.
c) ) \(\int\limits^8_5 {f(x)} \, dx\) , the value of this integral is greater than the value of integral b.
d) \(\int\limits^4_0 {f(x)} \, dx\), the value of this integral is greater than the value of integral a.
What is the function?
A function in mathematics from a set X to a set Y allocates exactly one element of Y to each element of X. The sets X and Y are collectively referred to as the function's domain and codomain, respectively. Initially, functions represented the idealized relationship between two changing quantities.
Here, we have
Given: the area under the graph of the function f for different intervals.
a) \(\int\limits^8_0 {f(x)} \, dx\): This integral represents the area under the graph of f from x = 0 to x = 8.
We can see that the area under the curve for this interval is negative since the curve is below the x-axis.
Hence, the value of this integral is negative.
b) \(\int\limits^8_5 {f(x)} \, dx\): This integral represents the area under the graph of f from x = 5 to x = 8.
We can see that the area under the curve for this interval is positive since the curve is above the x-axis.
Hence, the value of this integral is positive.
c) \(\int\limits^8_4 {f(x)} \, dx\): This integral represents the area under the graph of f from x = 4 to x = 8.
We can see that the area under the curve for this interval is greater than the area under the curve for interval b since the curve is higher above the x-axis.
Hence, the value of this integral is greater than the value of integral b.
d) \(\int\limits^4_0 {f(x)} \, dx\): This integral represents the area under the graph of f from x = 0 to x = 4.
We can see that the area under the curve for this interval is greater than the area under the curve for interval a since the curve is higher above the x-axis.
Hence, the value of this integral is greater than the value of integral a.
To learn more about the function from the given link
https://brainly.com/question/25638609
#SPJ4
Aeg = 10 solve for g
Answers
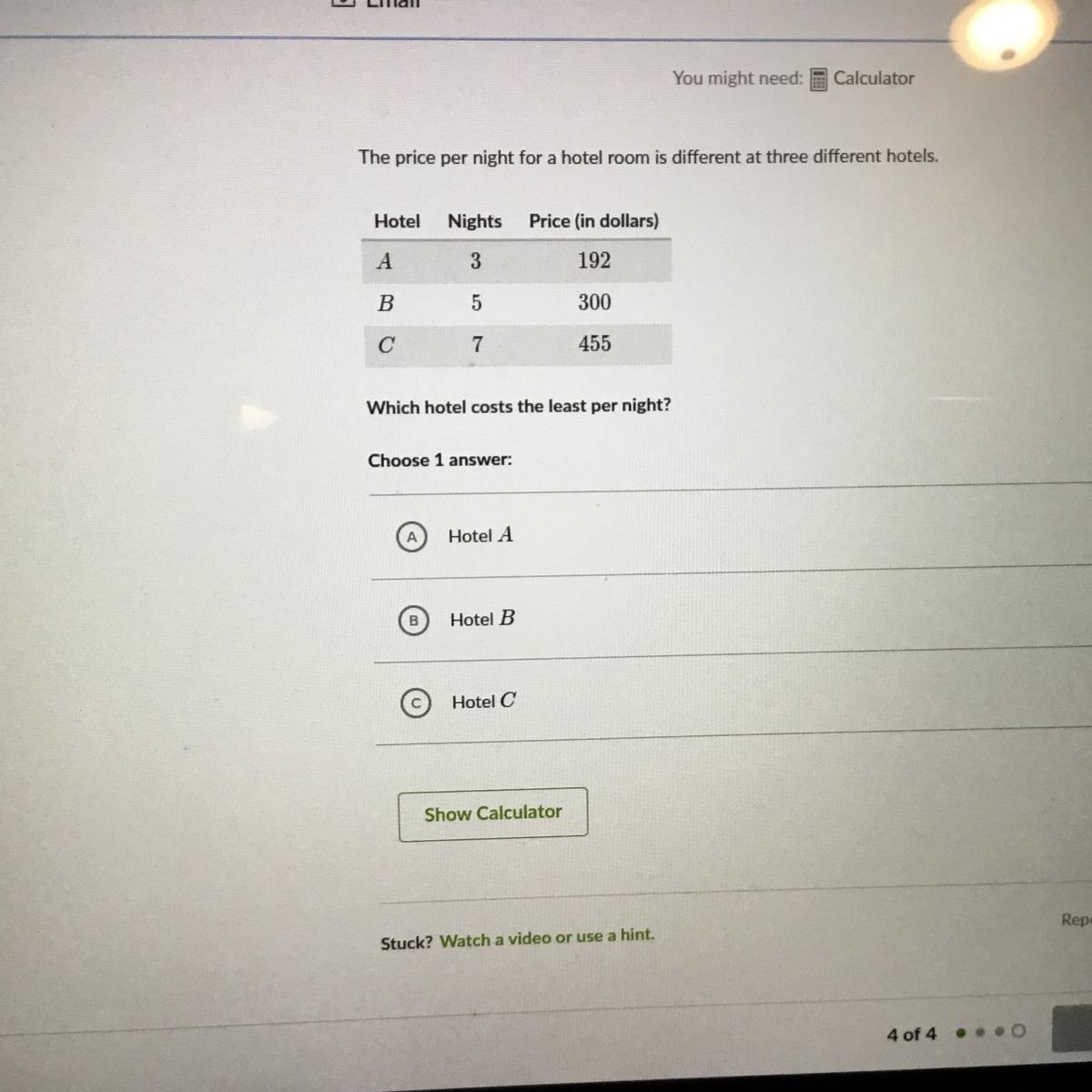
The price per night for a hotel room is different at three different hotels. Hotel Nights Price (in dollars) A AA 3 33 192 192192 B BB 5 55 300 300300 C CC 7 77 455 455455
Answers
Answer:
Hotel B is the least expensive
Step-by-step explanation:
Given
See attachment for clear details
Required
The least expensive
To do this, we simply divide the total cost by the number of nights to get the unit price
i.e.
\(Unit = \frac{Price}{Nights}\)
Hotel A
\(Nights = 3\\Price= 192\)
\(Unit = \frac{192}{3}\)
\(Unit = \$64\) per night
Hotel B
\(Nights = 5\\Price= 300\)
\(Unit = \frac{300}{5}\)
\(Unit = \$60\) per night
Hotel C
\(Nights = 7\\Price= 455\)
\(Unit = \frac{455}{7}\)
\(Unit = \$65\) per night
From the calculations above;
Hotel B is the least expensive because 60 is less than 64 and 65
Define a function in Scheme that
returns True if a matrix (list of lists) is symmetric and returns
False otherwise.
Answers
Here's a Scheme function that checks whether a matrix is symmetric or not:
```scheme
(define (is-symmetric-matrix matrix)
(define (get-element matrix i j)
(if (null? matrix)
#f
(if (= i 0)
(if (null? (car matrix))
#f
(if (= j 0)
(car (car matrix))
(get-element (cdr matrix) i (- j 1))))
(get-element (cdr matrix) (- i 1) j))))
(define (is-matrix-symmetric-helper matrix i j)
(if (null? matrix)
#t
(if (equal? (get-element matrix i j)
(get-element matrix j i))
(is-matrix-symmetric-helper matrix i (+ j 1))
#f)))
(if (null? matrix)
#t
(is-matrix-symmetric-helper matrix 0 0)))
```
The function `is-symmetric-matrix` takes a matrix as an input, which is represented as a list of lists. It uses a helper function called `is-matrix-symmetric-helper` to compare each element of the matrix with its corresponding element in the transposed position. The `get-element` function is used to retrieve the element at position `(i, j)` in the matrix.
The `is-matrix-symmetric-helper` function recursively iterates over the matrix, comparing each element with its transposed element. If any pair of corresponding elements is found to be different, it immediately returns `#f` (False), indicating that the matrix is not symmetric. If it reaches the end of the matrix without finding any differences, it returns `#t` (True), indicating that the matrix is symmetric.
Finally, the main `is-symmetric-matrix` function first checks if the matrix is empty. If it is, it immediately returns `#t` since an empty matrix is considered symmetric. Otherwise, it calls the helper function with the initial indices `(0, 0)` and returns its result.
Learn more about Scheme function: https://brainly.com/question/33167627
#SPJ11
A gallon of milk that cost $3.89 a year ago now costs $4.05. A. If the cost is increasing linearly, what is the growth rate? If the cost kept increasing in the same way, what will the milk cost 5 years from now? B. If the cost is increasing exponentially, what is the growth rate? What will the milk cost in 5 years?
Answers
Answer:
A) 1 = 0.16 = 16%
2) $4.69
B) 1 = 0.04 = 4%
2) $4.76
Step-by-step explanation:
A gallon of milk that cost $3.89 a year ago now costs $4.05.
A. Linear Growth rate formula:
P(t) = Po + rt
P(t) = Cost After t years = $4.05
Po = Initial cost = $3.89
1) If the cost is increasing linearly, what is the growth rate?
When t = 1
P(t) = Po + rt
4.05 = 3.89 + r × 1
r = 4.05 - 3.89
r = 0.16
Converting to percentage
= 0.16 × 100
= 16%
2) If the cost kept increasing in the same way, what will the milk cost 5 years from now?
P(t) = Po + rt
P(t) = 3.89 + 0.16 × 5
P(t) = 3.89 + 0.8
P(t) = 4.69
= $4.69
B. Exponential growth rate formula
P(t) = Po (1 + r)^t
If the cost is increasing exponentially, what is the growth rate?
1) when t = 1
P(t) = Cost After t years = $4.05
Po = Initial cost = $3.89
4.05 = 3.89 (1 + r)
Divide both sides by 3.89
4.05/3.89 = 3.89(1 + r)/3.89
1.0411311054 = 1 + r
r = 1.0411311054 - 1
r = 0.0411311054
Approximately = 0.04
Converting to Percentage
= 4%
2) What will the milk cost in 5 years?
P(t) = 3.89 (1 + r)^t
P(t) = 3.89 (1 + 0.0411311054)⁵
= $4.7585727225
Approximately = $4.76
need help for 20 points.....plzzzzz
a^2/16-5ab+100b^2
Answers
is it factorization ...
What is the answer ?

Answers
Answer:
y=400x+0
or simply
y=400x
Step-by-step explanation:
Ok slope= Rise over run
Y-intercept= point where x is 0
y-intercept= (0,0)
slope= 400/1=400
m=slope
b=y-intercept
y=mx+b
y=400x+0
Question 4 Given: csc 55° =, find tan 145° A. 514 B. - D. C. 2/ 314413 E. - / 6 pts
Answers
tan 145° is equal to csc 55°. Given that csc 55° is not provided in the options, none of the given options is correct. cotangent is the reciprocal of the sine function.
To find the value of tan 145°, we can use the relationship between tangent and cotangent:
tan x = 1 / cot x
Since cotangent is the reciprocal of the sine function, we can rewrite the given equation as:
csc 55° = 1 / sin 55°
To find the value of sin 55°, we can use the fact that sin x = cos (90° - x):
sin 55° = cos (90° - 55°)
= cos 35°
Now, we need to find the value of cos 35°. We can use a trigonometric identity:
cos (90° - θ) = sin θ
cos 35° = sin (90° - 35°)
= sin 55°
Substituting this value back into the equation, we have:
csc 55° = 1 / sin 55°
= 1 / cos 35°
Now, let's find the value of tan 145° using the relationship between tangent and cotangent:
tan 145° = 1 / cot 145°
Since cotangent is the reciprocal of the sine function, we can rewrite the equation as:
tan 145° = 1 / sin 145°
To find the value of sin 145°, we can use the fact that sin x = sin (180° - x):
sin 145° = sin (180° - 145°)
= sin 35°
Now, we have:
tan 145° = 1 / sin 145°
= 1 / sin 35°
Since we previously found that csc 55° = 1 / cos 35°, we can substitute this value into the equation:
tan 145° = 1 / sin 35°
= csc 55°
Therefore, tan 145° is equal to csc 55°. Given that csc 55° is not provided in the options, none of the given options is correct.
Learn more about reciprocal here
https://brainly.com/question/29863935
#SPJ11
Which expression is equivalent to 36 a minus 27?
Answers
Answer:
9(4a minus 3) is equivalent to 36a minus 27.
40 times 40 times 30 equals
Answers
48000 is your awnserrrr
U3U please help me asap U3U
the question is:
How is a system of equations created when each linear function is given as a set of two ordered pairs? Explain.
Answers
hate to be that person but what she said
bag contains 9 real diamonds and 5 fake diamonds. if 9 diamonds are picked from the bag at random, what is the probability that all of them are real?
Answers
The probability that all of them are real is 0.01875 or 1.875%
If the diamonds are replaced after each draw:
The probability of drawing a real diamond is 9/14, found by making the numerator the number of real diamonds and adding the total number of diamonds to find the denominator. 5+9 = 14.
To find the probability of all 9 diamonds drawn being real, multiply 9/14 by itself 9 times. = 387420489/ 20661046784. This creates a probability of 387420489/ 20661046784. This cannot be reduced because there is no common factor. To express as a decimal, divide. 387420489/ 20661046784 = 0.01875. To turn this into a percent, multiply by 100. 0.01875*100 = 1.875
Hence, the probability that all of them are real is 0.01875 or 1.875%
To learn more about probability click here:
brainly.com/question/29538993
#SPJ4
A guy wire supports a cell-phone tower. The guy wire makes a 55° angle with the ground and touches the ground 34 ft from the base of the tower. What is the length of the guy wire, rounded to the nearest foot? 20 ft 28 ft 49 ft 59 ft A right triangle. The base is labeled 34 feet. The angle made between the base and the hypotenuse is labeled 55 degrees. The angle made between the base and the perpendicular is marked as a right angle.
Answers
The length of the guy wire (rounded to the nearest foot) is 20 ft. Then the correct option is A.
What is a right-angle triangle?It is a type of triangle in which one angle is 90 degrees and it follows the Pythagoras theorem and we can use the trigonometry function.
A guy wire supports a cell phone tower.
The guy wire makes a 55° angle with the ground and touches the ground 34 ft from the base of the tower.
Base = 34 ft.
The length of the wire will be given as
\(\rm Wire \ length = 34 * cos\ 55^o\\\\Wire \ length = 19.5 \approx 20 \ ft\)
The length of the wire is 20 ft. Then the correct option is A.
More about the right-angle triangle link is given below.
https://brainly.com/question/3770177
Answer:
is 59ft
Step-by-step explanation:
just took the test

Given that a = (- 8) b = 2 c = 7 and d = 11 , solve for x, y, z, and w.
[[x + y, z], [z - x, w - y]] =
[[a, b], [c, d]]
What is the value of w?
(Only type a number, nothing else)
Answers
Answer:
24
Step-by-step explanation:
Okay, let's solve this step-by-step:
1) We are given: a = -8, b = 2, c = 7, d = 11
2) We are asked to solve the matrix equation: [[x + y, z], [z - x, w - y]] = [[a, b], [c, d]]
3) Matching up the elements in the matrices:
x + y = a = -8 (1)
z = b = 2 (2)
z - x = c = 7 (3)
w - y = d = 11 (4)
4) Solving the equations:
From (1): x + y = -8 => x = -8 - y
Substitute in (3): z - (-8 - y) = 7 => z - (-8) = 7 + y => z = 15 + y
Substitute (2) into the above: 2 = 15 + y => y = 13
Substitute y = 13 into (1): -8 - 13 = -21 = x
Substitute x = -21 and y = 13 into (4): w - 13 = 11 => w = 11 + 13 = 24
Therefore, the values are:
x = -21
y = 13
z = 15
w = 24
So the final value of w is:
w = 24
HELP ASAPPPP PLEASE I NEED TO FINISH ASAP

Answers
Answer:
-15.3, -15.1, -12.3, -11.4, -11.4, 19.6
Step-by-step explanation:
-15.3, -15.1, -12.3, -11.4, -4.3, 19.6
Honored! You are my 100th Math Answer!
A swimming pool is 20 feet wide and 40 feet long. If it is surrounded by a walkway of square tiles, each is 1 foot by 1 foot, how much area do the pool and walkway cover?
Answers
Answer:
124 tiles
Step-by-step explanation:
2(20+40)
2(60)
120+4=124
Please answer correctly !!!!!!! Will mark brainliest !!!!!!!!!!!!!

Answers
Martha needs 28 strawberries for every 4 smoothies she makes. plete the table using equivalent ratios.

Answers
Answer:
strawberries smoothies
28 4
21 3
70 10
Step-by-step explanation:
hello everyone please I need help with this question quickly!
The table shows some information about the lifetimes, t, in hours, of some lightbulbs.
Lifetime Frequency
25 < t ≤ 50 100
50 < t ≤ 100 45
100 < t ≤ 150 67
150 < t ≤ 200 50
200 < t ≤ 250 0
250 < t ≤ 300 12
300 < t ≤ 350 16
Estimate the mean lifetime of a bulb.
Give your answer rounded to 2 DP.
Answers
Answer:
112.93
Explanation:
\(\sf \boxed{\sf Mean= \frac{interval \ midpoint \ x \ frequency }{Total \ Frequency} }\)
Solving Stepwise:
\(\rightarrow \sf \dfrac{37.5 \ x \ 100 \ + \ 75 \ x \ 45 \ + \ 125 \ x \ 67 \ + \ 175 \ x \ 50 \ + \ 225 \ x \ 0 \ + \ 275 \ x \ 12 \ + \ 325 \ x \ 16 }{100 + 45 +67+50+0+12+16}\)
\(\rightarrow \sf \dfrac{32750}{290}\)
\(\rightarrow \sf \dfrac{3275}{29}\)
\(\rightarrow \sf 112.9310345\)
\(\rightarrow \sf 112.93 \ (rounded \ to \ nearest \ 2 \ decimal \ places)\)
If a fair coin is tossed 8 times, what is the probability, rounded to the nearest thousandth, of getting at least 7 heads?
Answers
The required probability of getting at least 7 heads is 1/128 or 0.0078
What is probability ?Probability shows possibility to happen an event, it defines that an event will occur or not. The probability varies from 0 to 1.
Given that,
A fair coin is tossed = 8 time.
We have to find the probability of getting at least 7 heads.
Since, the probability of getting head, when one coin is tossed = 1/2
And the probability of getting tale = 1/2
The probability of getting head at least 7 times when coin is tossed 8 times can be given as,
The head can come 7 times, then probability = (1/2)⁷(1/2) = (1/2)⁸
The head can come 8 times, then probability = (1/2)⁸
The probability of getting head at least 7 times
= (1/2)⁸ + (1/2)⁸ = 2(1/2)⁸ = (1/2)⁷ = 1/128 = 0.0078
The probability of getting at least 7 heads is 1/128 or 0.0078
To know more about Probability on:
https://brainly.com/question/12478394
#SPJ1
For what values of the variable is the rational expression undefined?
5x +4/ x2-1
Answers
Answer:
When x = 1 or -1.
Step-by-step explanation:
When the denominator x^2-1 is zero the expression is undefined.
So the values of x cannot be 1 or -1.
the moellers drove from new york to san francisco, a distance of 3,000 miles. the first day, they drove of the distance and of the remaining distance on the second day. how many miles did they have remaining to reach their destination?
Answers
The Moellers had 1,500 miles remaining to reach their destination. On the first day, the Moellers drove 1/2 (or 0.5) of the 3,000 miles, which is 1,500 miles. This means they had 1,500 miles remaining to reach their destination.
On the second day, they drove 1/4 (or 0.25) of the remaining 1,500 miles, which is 375 miles. Therefore, they had 1,125 miles remaining to reach their destination after driving 1/2 on the first day and 1/4 on the second day.
Based on the given information, the Moellers drove 1/3 of the distance on the first day and 1/4 of the remaining distance on the second day. Let's calculate the remaining distance to reach their destination:
Total distance: 3,000 miles
First day: 1/3 of 3,000 miles = 1,000 miles
Remaining distance after the first day: 3,000 - 1,000 = 2,000 miles
Second day: 1/4 of 2,000 miles = 500 miles
Remaining distance after the second day: 2,000 - 500 = 1,500 miles
So, the Moellers had 1,500 miles remaining to reach their destination.
Visit here to learn more about distance brainly.com/question/15172156
#SPJ11
Solve one, any question you want, please show work,

Answers
Answer:
Step 1: Variables are q for quarters and d for dimes. So d = dimes and q = quarters
Step 2: The two equations that form a system of equations are:
\(\left \{ {{0.1d+.25q=3.70} \atop {d+q=19}} \right.\)
Step 3: Work is shown on the attachment and on the step-by-step explanation
Step 4: Given the context of the problem, the solution of the amount of dimes and quarters, which is 7 dimes and 12 quarters, is needed to satisfy both systems to concur that there was 7 dimes and 12 quarters in a sum of money that amounted to $3.70 with 19 coins in total.
Step-by-step explanation:
Step 1: To first attempt to solve this, we must have to set up two variables for the amount of value a quarter and a dime has. So since a quarter is worth 0.25¢ in and a dime is worth 0.10¢, then we can set up one of the equations to be:
\(0.1d + .25q = 3.70\)
And we set it to equal the $3.70 because that's the amount that the sum of money totals to.
Step 2: Now to get the other side of the equation, we use the variables again, d and q and set that to equal 19 because that is the amount of coins that there is in total.
Step 3: Now that we have both equations, we can solve the problem now.
\(\left \{ {{0.1d+.25q=3.70} \atop {d+q=19}} \right.\)
Let's first solve this equation by setting one of the side's variables the same absolute value, but not the same integer value so that we can cross it off. I will choose the equation \(d+q=19\) to be multiplied by -.1 so that we can cross off both 0.1d and -0.1d after the result of the multiplication:
\(\left \{ {{0.1d+.25q=3.70} \atop {-.1d+-.1q=-1.9}} \right.\)
Now, lets cross off everything that we can, and add up the variables together. This includes adding .25q + (-.1q) and adding 3.70 + -1.9.
Now we have:
\(\left \{ {{.25q=3.70} \atop {-.1q=-1.9}} \right.\)
Now, what we do from here is add the left side and the right side side to get one equation, which is:
\(.15q=1.8\)
Finally, we divide both sides to get q=12, which means that there are 12 quarters. Since there are 19 coins in total, we can subtract 12 from 9 to get the remaining amount of dimes, which is 7.
In conclusion, q=12 and d=7.
My written work is also provided in the attachment!!!
Step 4: What does this mean in the context of the question?
This basically means that the solution of the amount of dimes and quarters, which is 7 dimes and 12 quarters, is needed to satisfy both systems to concur that there was 7 dimes and 12 quarters in a sum of money that amounted to $3.70 with 19 coins in total.
In simpler terms, this means that we need 7 dimes and 12 quarters to satisfy that there was a sum of money that amounted to $3.70 with 19 coins in total .

a recipe uses 1/4 cup of water and 2 cups of flour.write the ratio of water to flour.then find the value of the ratio
Answers
The ratio of water to flour in the recipe is 1 : 8. This means that for every 1 unit of water, we need 8 units of flour in the recipe.
In the given recipe, the amount of water used is 1/4 cup and the amount of flour used is 2 cups. The ratio of water to flour in the recipe can be expressed as a fraction, where the numerator is the amount of water used and the denominator is the amount of flour used. This gives the ratio of water to flour as 1/4 : 2.
To simplify the ratio, we can find the common factor that will eliminate the fractional value of water. In this case, we can multiply both sides of the ratio by 4 to get 1 : 8. This means that for every 1 unit of water, we need 8 units of flour in the recipe.
To learn more about ratio please click on below link
https://brainly.com/question/13419413
#SPJ1